Journal of Applied Mathematics and Physics
Vol.05 No.11(2017), Article ID:80368,13 pages
10.4236/jamp.2017.511180
Positive Radial Solutions for a Class of Semilinear Elliptic Problems Involving Critical Hardy-Sobolev Exponent and Hardy Terms
Yong-Yi Lan
School of Sciences, Jimei University, Xiamen, China

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 6, 2017; Accepted: November 14, 2017; Published: November 17, 2017
ABSTRACT
In this paper, we investigate the solvability of a class of semilinear elliptic equations which are perturbation of the problems involving critical Hardy-So- bolev exponent and Hardy singular terms. The existence of at least a positive radial solution is established for a class of semilinear elliptic problems involving critical Hardy-Sobolev exponent and Hardy terms. The main tools are variational method, critical point theory and some analysis techniques.
Keywords:
Hardy Singular Terms, Hardy-Sobolev Exponent, Positive Radial Solution, Perturbation Method, Variational Approach

1. Introduction and Main Results
In this paper, we are concerned with the existence of positive radial solutions for the following semilinear elliptic problem with Hardy-Sobolev exponent and Hardy singular terms:
(1.1)
where is the Hardy-Sobolev critical exponent and is the Sobolev critical exponent, . denotes the space of the functions such that , endowed with scalar product and norm, respectively, given by
that coincides with the completion of with respect to the L2-norm of the gradient. By Hardy inequality [1] , we easily derive that the norm is equivalent to the usual norm:
in .
Clearly, is a closed subset of , so is a Hilbert space. By the symmetric criticality principle, in view of [2] , we know that the positive radial solutions of problem (1.1) correspond to the nonzero critical points of the functional defined by
where .
The reason why we investigate (1.1) is the presence of the Hardy-Sobolev exponent, the unbounded domain and the so-called inverse square potential in the linear part, which cause the loss of compactness of embedding , and . Hence, we face a type of triple loss of compactness whose interacting with each other will result in some new difficulties. In last two decades, loss of compactness leads to many interesting existence and nonexistence phenomena for elliptic equations. There are abundant results about this class of problems. For example, by using the concentration compactness principle, the strong maximum principle and the Mountain Pass lemma, Li et al. [3] had obtained the existence of positive solutions for singular elliptic equations with mixed Dirichlet-Neumann boundary conditions involving Sobolev-Hardy critical exponents and Hardy terms. Bouchekif and Messirdi [4] obtained the existence of positive solution to the elliptic problem involving two different critical Hardy-Sobolev exponents at the same pole by variational methods and concentration compactness principle. Lan and Tang [5] have obtained some existence results of (1.1) with via an abstract perturbation method in critical point theory. There are some other sufficient conditions, we refer the interested readers to ( [6] - [18] ) and the references therein.
In the present paper, we investigate the existence of positive radial solutions of problem (1.1). There are several difficulties in facing this problem by means of variational methods. In addition to the lack of compactness, there are more intrinsic obstructions involving the nature of its critical points. Based on a suitable use of an abstract perturbation method in critical point theory discussed in [5] [13] [14] , we show that the semilinear elliptic problem with Hardy-Sobolev exponent and Hardy singular terms has at least a positive radial solution.
In this paper, we assume that h satisfies one of the following conditions:
(H) , and
for some .
(H’) , is T-periodic and
The main results read as follows.
Theorem 1 Let (H) hold, and assume that and . Then for small, problem (1.1) has a positive radial solution .
Remark 1 It is easy to check that the following function satisfies the conditions of Theorem 1,
Theorem 2 If assumption (H) holds, and suppose that and . Then for small, problem (1.1) has a positive radial solution .
Remark 2 It is easy to check that the following function satisfies the conditions of Theorem 2,
Theorem 3 Assume that (H) holds, and suppose
and
Then for small, problem (1.1) has a positive radial solution .
Remark 3 It is easy to check that the following function satisfies the conditions of Theorem 3 for all and ,
in fact,
and
We can also give the following example for and ,
in fact, with the help of computers, we can get
and
Theorem 4 Suppose that assumption (H’) holds, and satisfies the condition that . Then problem (1.1) has a positive radial solution , provided .
Remark 4 It is easy to check that the following function satisfies the conditions of Theorem 4,
in fact,
and by a direct computation, we have
Theorem 5 Let h satisfy (H’), and suppose that and . Then problem (1.1) has a positive radial solution , provided .
Remark 5 It is easy to check that the following function satisfies the conditions of Theorem 5,
This paper is organized as follows. After a first section we devoted to studying
the unperturbed problem . The main results are proved
in Section 3. In the following discussion, we denote various positive constants as
C or for convenience. denote as .
This idea is essentially introduced in [5] [13] .
2. The Case
In this section, we will study the unperturbed problem
(2.1)
It is well-known that the nontrivial solutions of problem (2.1) are equivalent to the nonzero critical points of the energy functional
Obviously, the energy functional is well-defined and is of with derivatives given by
For all , it is well known that the function
solves the equation (2.1) and satisfies
Let
then
has a (non-compact) 1-dimensional critical manifold given by
The unperturbed problem is invariant under the transformation that
transforms the function in the function . The purpose of this
section is to show the following lemmas.
Lemma 2.1. For all , .
Proof. We will prove the lemma by taking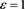 , hence
, hence . The case of a general
. The case of a general 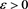 will follow immediately. It is always true that
will follow immediately. It is always true that 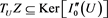 . We will show the converse, i.e., that if
. We will show the converse, i.e., that if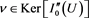 , namely
, namely  is a solution of
is a solution of
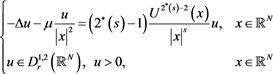 (2.2)
(2.2)
then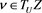 , namely
, namely 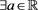 such that
such that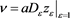 , where
, where 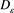 denotes the
denotes the
derivatives with respect to the parameter . We look for solutions
. We look for solutions 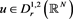 of problem (2.2). One has
of problem (2.2). One has

and then a first solution is given by
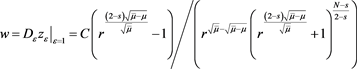
which belongs to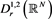 , where
, where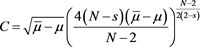 . If we
. If we
look for a second independent solution of the form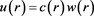 , we will check that u is not in
, we will check that u is not in
and because 
Setting
namely
where C is a constant. This implies 
as



This completes the proof of Lemma. ,
Lemma 2.2. For all

Proof. Indeed, 


It is obviously that 


Moreover, fox fixed
is a bounded linear functional in




Clearly 









which implies that 

So



Now, we give the abstract perturbation method, which is crucial in our proof of the main results of this paper.
Lemma 2.3. [13] (Abstract Perturbation Method) Let E be a Hilbert space and let 

Suppose that 
1) 


2) for all

3) for all

Hereafter we denote by 

Let 


1) 
2) 
3) 








Remark 2.4. [13] If 



3. Proof of the Theorems
We will now solve the bifurcation equation. In order to do this, let us define the reduced functional, see [14] ,
where 


The functional 

Here we will prove the existence result by showing that problem (1.1) has a positive radial solution provided that h satisfies some integrability conditions. Before giving the proof of the main results, we need the following lemma.
Lemma 3.1. If (H) holds, then 

Proof. From the definition of 
where
so we have
we deduce that 

Proof of Theorem 1. Firstly, we claim that 
that will be used in the following discussion. If
M is nothing but the Mellin transform. The associated convolution is defined by
From the definition, it follows that
With this notation we can write our 
We set 
Note that

if, by contradiction, 

On the other hand, 







Proof of Theorem 2. Using Lemma 3.1, we have 





and the condition 





Proof of Theorem 3. It suffices to remark that
If
then 



In the rest of the section we will give the proof of Theorem 4 and Theorem 5. First we give the following Lemma. Hypothesis (H’) allows us to use the following Riemann-Lebesgue convergence result.
Lemma 3.2 [13] Let 



Lemma 3.3 If (H’) holds, then
Proof. Given

On the other hand, the remainder integral over the interval 

Proof of Theorem 4. Using Lemma 3.3, we have 





and the condition 





Proof of Theorem 5. It suffices to repeat the arguments used to prove Theorem 1 using Lemma 3.1 instead of Lemma 3.3.
4. Conclusion
We study a class of semilinear elliptic problems involving critical Hardy-Sobolev exponent and Hardy terms, and obtain positive radial solutions for these problems via an abstract perturbation method in critical point theory. Extensions of nonradial solutions for these problems are being investigated by the author. Results will be submitted for publication in the near future.
Acknowledgements
We would like to thank the editor and the referee for their valuable comments which have led to an improvement of the presentation of this paper.
Fund
This work is supported by Natural Science Foundation of China (No. 11671331); Natural Science Foundation of Fujian Province (No. 2015J01585) and Scientific Research Foundation of Jimei University.
Cite this paper
Lan, Y.-Y. (2017) Positive Radial Solutions for a Class of Semilinear Elliptic Problems Involving Critical Hardy-Sobolev Exponent and Hardy Terms. Journal of Applied Mathematics and Physics, 5, 2205-2217. https://doi.org/10.4236/jamp.2017.511180
References
- 1. Garcia Azorero, J.P. and Peral Alonso, I. (1998) Hardy Inequalities and Some Critical Elliptic and Parabolic Problems. Journal of Differential Equations, 144, 441-476. https://doi.org/10.1006/jdeq.1997.3375
- 2. Palais, R.S. (1979) The Principle of Symmetric Criticality. Communications in Mathematical Physics, 69, 19-30. https://doi.org/10.1007/BF01941322
- 3. Li, Y.Y., Ruf, B., Guo, Q.Q. and Niu, P.C. (2014) Positive Solutions for Singular Elliptic Equations with Mixed Dirichlet-Neumann Boundary Conditions. Mathematische Nachrichten, 287, 374-397. https://doi.org/10.1002/mana.201100351
- 4. Bouchekif, M. and Messirdi, S. (2015) On Elliptic Problems with Two Critical Hardy-Sobolev Exponents at the Same Pole. Applied Mathematics Letters, 42, 9-14. https://doi.org/10.1016/j.aml.2014.10.012
- 5. Lan, Y.Y. and Tang, C.L. (2014) Perturbation Methods in Semilinear Elliptic Problems Involving Critical Hardy-Sobolev Exponent. Acta Mathematica Scientia, 34B, 703-712. https://doi.org/10.1016/S0252-9602(14)60041-2
- 6. Yan, S.S. and Yang, J.F. (2013) Infinitely Many Solutions for an Elliptic Problem Involving Critical Sobolev and Hardy-Sobolev Exponents. Calculus of Variations and Partial Differential Equations, 48, 587-610. https://doi.org/10.1007/s00526-012-0563-7
- 7. Ding, L. and Tang, C.L. (2008) Existence and Multiplicity of Positive Solutions for a Class of Semilinear Elliptic Equations Involving Hardy Term and Hardy-Sobolev Critical Exponents. Journal of Mathematical Analysis and Applications, 339, 1073-1083. https://doi.org/10.1016/j.jmaa.2007.07.066
- 8. Shang, Y.Y. and Tang, C.L. (2009) Positive Solutions for Neumann Elliptic Problems Involving Critica Hardy-Sobolev Exponent with Boundary Singularities. Nonlinear Analysis: Theory, Methods & Applications, 70, 1302-1320. https://doi.org/10.1016/j.na.2008.02.013
- 9. Cao, D.M., He, X.M. and Peng, S.J. (2005) Positive Solutions for Some Singular Critical Growth Nonlinear Elliptic Equations. Nonlinear Analysis: Theory, Methods & Applications, 60, 589-609. https://doi.org/10.1016/j.na.2004.08.042
- 10. Cao, D.M. and Peng, S.J. (2003) A Note on the Sign-Changing Solutions to Elliptic Problems with Critical Sobolev and Hardy Terms. Journal of Differential Equations, 193, 424-434. https://doi.org/10.1016/S0022-0396(03)00118-9
- 11. Ghoussoub, N. and Kang, X.S. (2004) Hardy-Sobolev Critical Elliptic Equations with Boundary Singularities. Annales de l’Institut Henri Poincaré C, Analyse non linéaire, 21, 767-793.
- 12. Kang, D.S. and Peng, S.J. (2005) Solutions for Semi-Linear Elliptic Problems with Critical Hardy-Sobolev Exponents and Hardy Potential. Applied Mathematics Letters, 18, 1094-1100.
- 13. Wang, C. and Shang, Y.Y. (2017) Existence and Multiplicity of Positive Solutions for Elliptic Equation with Critical Weighted Hardy-Sobolev Exponents and Boundary Singularities. Computers Mathematics with Applications, 74, 701-713.
- 14. Wang, C. and Shang, Y.Y. (2017) Existence and Multiplicity of Positive Solutions for a Perturbed Semilinear Elliptic Equation with Two Hardy-Sobolev Critical Exponents. Journal of Mathematical Analysis and Applications, 451, 1198-1215.
- 15. Bhakta, M. (2017) Infinitely Many Sign-Changing Solutions of an Elliptic Problem Involving Critical Sobolev and Hardy-Sobolev Exponent. Proceedings of the Indian Academy of Sciences-Mathematical Sciences, 127, 337-347. https://doi.org/10.1007/s12044-016-0304-5
- 16. Deng, Z.Y. and Huang, Y.S. (2017) Positive Symmetric Results for a Weighted Quasilinear Elliptic System with Multiple Critical Exponents in RN, Boundary Value Problems. https://doi.org/10.1186/s13661-017-0758-0
- 17. Ambrosetti, A., Garcia Azorero, J. and Peral, I. (1999) Perturbation of , the Scalar Curvature Problem in RN, and Related Topics. Journal of Functional Analysis, 165, 117-149. https://doi.org/10.1006/jfan.1999.3390
- 18. Ambrosetti, A. and Malchiodi, A. (2006) Perturbation Methods and Semilinear Elliptic Problems on Rn. Birkh?user Verlag.�





































