Journal of Applied Mathematics and Physics
Vol.04 No.10(2016), Article ID:71615,13 pages
10.4236/jamp.2016.410196
Study of Temperature Behaviour on Thermally Induced Vibration of Non-Homogeneous Trapezoidal Plate with Bi-Linearly Varying Thickness
Kavita1*, Satish Kumar1, Pragati Sharma2
1Department of Mathematics, M. M. University, Mullana, India
2Department of Mathematics, Haryana College of Technology and Management, Kaithal, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 10, 2016; Accepted: October 25, 2016; Published: October 28, 2016
ABSTRACT
The main aim of the present work is to study the linear temperature behaviour of a non-homogeneous trapezoidal plate whose thickness varies linearly in both directions. The temperature behaviour considered linear along the length of the plate. Non-homogeneity in plate arises due to variation in density along the length of the plate. The two-term deflection function with clamped-simply supported-clamped- simply supported boundary condition is taken into consideration. The effect of structural parameters such as taper constants, thermal gradient, non-homogeneity constant and aspect ratio has been studied. Rayleigh-Ritz method is used to solve the governing differential equations and to obtain the fundamental frequencies for the first two modes of vibration. Results are presented in graphical form.
Keywords:
Vibration, Trapezoidal Plate, Taper Constants, Thermal Gradient, Aspect Ratio, Non-Homogeneity, Thickness, Density, Frequencies

1. Introduction
Most of the machines and structures work under the control of high temperature. Due to this, system undergoes some vibrations. Vibrations affect the efficiency, strength and durability of the system. The purpose of vibration study is to reduce vibration through proper and accurate design of machines and structures. Therefore, it is necessary for researchers and design engineers to have pre-knowledge of vibrational characteristics of systems before finalizing the design of structures. The vibrational analysis of plates depends on their geometry. In modern technology, plates of different shapes such as rectangular, circular, elliptical, parallelogram etc. are used in engineering applications. Plates with different shapes, boundary conditions at the edges and various complicating effects have often found applications in different structures such as aerospace, machine design, telephone industry, nuclear reactor technology, naval structures and earthquake-resistant structures. Literature shows that the vibration analysis has inspired many researchers to do work in this direction. Out of them few are given under. Gupta and Sharma [1] had analyzed the effect of linear thermal gradient on vibrations of trapezoidal plates whose thickness varied parabolically. Gupta and Sharma [2] had studied the effect of linear temperature behaviour on a non-homogeneous trapezoidal plate of parabolically varying thickness. Leissa [3] provided an appreciable collection of research papers in his monograph on the vibration of plates of different shapes and under different boundary conditions. Singh and Saxena [4] discussed the transverse vibration of triangular plates with variable thickness. Chen et al. [5] had worked on the free vibration of cantilevered symmetrically laminated thick trapezoidal plates. Bambill et al. [6] studied the transverse vibrations of rectangular, trapezoidal and triangular orthotropic, cantilever plates. Saliba [7] worked on free vibration analysis of simply supported symmetrical trapezoidal plates. Krishnan and Deshpande [8] studied the free vibration of trapezoidal plates. Liew and Lam [9] had studied the vibrational response of symmetrically laminated trapezoidal composite plates with point constraints. Liew and Lim [10] worked on the transverse vibration of symmetric trapezoidal plates of variable thickness. Liew [11] discussed the vibration of symmetrically laminated cantilever trapezoidal composite plates. Klein [12] analyzed the vibration of simply supported isosceles trapezoidal flat plates. Qatu [13] discussed the vibrations of laminated composite completely free triangular and trapezoidal plates. Zamani et al. [14] studied the free vibration analysis of moderately thick trapezoidal symmetrically laminated plates with various combinations of boundary conditions. Manna [15] calculated the free vibration of tapered isotropic rectangular plates with linearly varying thickness by using a high- order triangular element. Bhardwaj et al. [16] had studied the transverse vibrations of clamped and simply-supported circular plates with two dimensional thickness variations. Mirza and Bijlani [17] discussed the vibration of triangular plates of variable thickness. Gupta et al. [18] worked on vibration of non-homogeneous circular mindlin plates with variable thickness. Narita et al. [19] observed the transverse vibration of clamped trapezoidal plates having rectangular orthotropy. Zhou and Zheng [20] worked on the vibration of skew plates by the MLS-Ritz method. Quintana and Nallim [21] presented a variational approach to free vibration analysis of shear deformable polygonal plates with variable thickness. Korobko and Chernyaev [22] determinated the maximum deflection in transverse bending of parallelogram plates using the conformal radiuses ratio.
After a careful study of literature, it is recognized that no work has been done on linear density variation with bilinear thickness variation on vibration of heated trapezoidal plate. In this paper, an analysis is presented to study the effect of thermally induced vibration of non-homogeneous trapezoidal plate with bi-linearly varying thickness. To acquire the natural frequencies for the first two modes of vibration, Rayleigh- Ritz’s method is used for a non-homogeneous trapezoidal plate whose two sides are clamped and two are simply-supported.
2. Thickness and Density
As depicted in Figure 1 a symmetric, non-homogeneous trapezoidal plate has been considered. Thickness varies bilinearly along length and width of the plate as
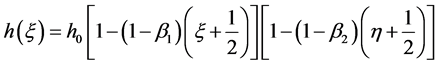 (1)
(1)
where 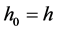 at
at 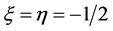 and
and 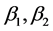 are taper constants.
are taper constants.
The density is one of the most important aspects of any design. Due to variation in density, non-homogeneity occurs in plate’s material which varies linearly along the length of the plate. So, it can be considered as
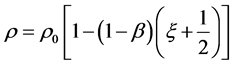 (2)
(2)
where  is the mass density at
is the mass density at  and
and 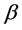 is non-homogeneity constant.
is non-homogeneity constant.
The temperature of the trapezoidal plate varies linearly along the length of the plate as
Figure 1. Geometry of the trapezoidal plate.
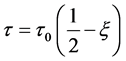 (3)
(3)
where  denotes the excess above the reference temperature at a distance
denotes the excess above the reference temperature at a distance 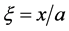 and
and 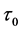 denotes the temperature excess above the reference temperature at the end
denotes the temperature excess above the reference temperature at the end ..
..
For most of the structural materials the temperature dependence of the modulus of elasticity is given by Nowacki [23] as
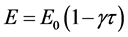 (4)
(4)
where 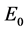 is Young’s modulus value at reference temperature
is Young’s modulus value at reference temperature 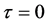 and
and 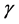 is the slope of variation of
is the slope of variation of 

By the use of Equation (3) in Equation (4), one obtains

where 
3. Governing Differential Equations
The governing differential equations of kinetic energy T and strain energy V for a trapezoidal plate are given by [10] as

and

where 

Flexural rigidity of the plate 

where 

By using Equation (5) and Equation (9) in Equation (8), the flexural rigidity becomes

Using Equation (1) and Equation (2) in Equation (6), we get

Using Equation (10) in Equation (7), we get

In the present study the two term deflection function which satisfies the boundary condition can be expressed as

where 


4. Methodology
For the existing problem, Rayleigh-Ritz’s method has been employed. It requires the maximum strain energy must be equal to the maximum kinetic energy. Therefore, it is necessary that the consequent equation must be satisfied

Using Equation (14) into Equation (11) and Equation (12), we obtain

And

Using Equation (16) and Equation (17) into Equation (15), we get

where


And

is a frequency parameter.
The unknowns 



On simplifying (22), we get

where 
For a non-zero solution, the determinant of co-efficient of Equation (23) must be zero. Thus the frequency Equation for a (C-S-C-S) trapezoidal plate is given by

On simplifying Equation (24), a quadratic equation in 

5. Results and Discussions
Frequencies for the first two modes of vibration are calculated for non-homogeneous trapezoidal plate whose thickness varies linearly in both directions and density varies linearly in x-direction. Different values of taper constants 




In Figure 2(a) and Figure 2(b) these figures show the variation of the frequency parameter 



Figure 2. (a) Variation of frequency parameter 



1)
2)
3)
4)
These figures demonstrate that as the taper constant 

In Figure 3(a) and Figure 3(b), these figures show the variation of the frequency parameter 



Figure 3. (a) Variation of frequency parameter 



1)
2)
3)
4)
These figures explain that as the taper constant 

In Figure 4(a) and Figure 4(b) these figures depict the behaviour of the frequency parameter 



Figure 4. (a) Variation of frequency parameter 



1)
2)
3)
4)
It is clear from these figures that as the thermal gradient 

In Figure 5(a) and Figure 5(b) these figures demonstrate the effect of aspect ratio c/b (varying from 0.25 to 1.0) on the frequency parameter 


Figure 5. (a) Variation of frequency parameter 

1)
2)
a)
b)
c)
d)
It is evident from the figures that as aspect ratio c/b increases, the frequency parameter decreases for both the modes of vibration. From Figure 5(a) and Figure 5(b) it is observed that with increase in aspect ratio a/b the frequency increases for both the modes of vibration.
In Figure 6(a) and Figure 6(b) these figures show the effect of non-homogeneity constant 



Figure 6. (a) Variation of frequency parameter 



1)
2)
3)
These figures show that as the non-homogeneity constant 

6. Conclusion
In the present paper, the effect of temperature on the vibration of symmetric, non-ho- mogeneous trapezoidal plate of isotropic material with clamped-simply supported- clamped-simply supported-boundary condition has been studied by using the Rayleigh-Ritz method. Effect of other plate’s parameters such as non-homogeneity constant, aspect ratios, taper constants has also been considered. It is obvious from the graphs that by the increase of taper constants, aspect ratio a/b the frequency of both the modes of vibration increases. On the other hand, frequency decreases with increasing values of thermal gradient, aspect ratio c/b and non-homogeneity constant for both the modes of vibration. By the proper selection of various plate parameters such as taper constants, thermal gradient, aspect ratio and non-homogeneity constant, a desired frequency can be attained for the first two modes of vibration which would be helpful for the design engineers.
Cite this paper
Kavita, Kumar, S. and Sharma, P. (2016) Study of Temperature Behaviour on Thermally Induced Vibration of Non-Homogeneous Trapezoidal Plate with Bi-Linearly Varying Thickness. Journal of Applied Mathematics and Physics, 4, 1936-1948. http://dx.doi.org/10.4236/jamp.2016.410196
References
- 1. Gupta, A.K. and Sharma, P. (2012) Effect of Linear Thermal Gradient on Vibrations of Trapezoidal Plates Whose Thickness Varies Parabolically. Journal of Vibration and Control, 18, 395-403.
http://dx.doi.org/10.1177/1077546311409266 - 2. Gupta, A.K. and Sharma, P. (2013) Study of the Effect of Linear Temperature Behaviour on a Non-Homogeneous Trapezoidal Plate of Parabolically Varying Thickness. International Journal of Acoustics and Vibration, 18, 117-123.
http://dx.doi.org/10.20855/ijav.2013.18.3324 - 3. Leissa, A.W. (1969) Vibration of Plates, NASA SP-160.
- 4. Singh, B. and Saxena, V. (1996) Transverse Vibration of Triangular Plates with Variable Thickness. Journal of Sound and Vibration, 194, 471-496.
http://dx.doi.org/10.1006/jsvi.1996.0373 - 5. Chen, C.C., Kitipornchai, S., Lim, C.W. and Liew, K.M. (1999) Free Vibration of Cantilevered Symmetrically Laminated Thick Trapezoidal Plates. International Journal of Mechanical Sciences, 41, 685-702.
http://dx.doi.org/10.1016/S0020-7403(98)00025-3 - 6. Bambill, D.V., Laura, P.A.A. and Rossi, R.E. (1998) Transverse Vibrations of Rectangular, Trapezoidal and Triangular Orthotropic, Cantilever Plates. Journal of Sound and Vibration, 210, 286-290.
http://dx.doi.org/10.1006/jsvi.1997.1268 - 7. Saliba, H.T. (1986) Free Vibration Analysis of Simply Supported Symmetrical Trapezoidal Plates. Journal of Sound and Vibration, 110, 87-97.
http://dx.doi.org/10.1016/S0022-460X(86)80076-1 - 8. Krishnan, A. and Deshpande, J.V. (1991) A Study on Free Vibration of Trapezoidal Plates. Journal of Sound and Vibration, 146, 507-515.
http://dx.doi.org/10.1016/0022-460X(91)90705-O - 9. Liew, K.M. and Lam, K.Y. (1992) Vibrational Response of Symmetrically Laminated Trapezoidal Composite Plates with Point Constraints. International Journal of Solids and Structures, 29, 1535-1547.
http://dx.doi.org/10.1016/0020-7683(92)90132-D - 10. Liew, K.M. and Lim, M.K. (1993) Transverse Vibration of Trapezoidal Plates of Variable Thickness: Symmetric Trapezoids. Journal of Sound and Vibration, 165, 45-67.
http://dx.doi.org/10.1006/jsvi.1993.1242 - 11. Liew, K.M. (1992) Vibration of Symmetrically Laminated Cantilever Trapezoidal Composite Plates. International Journal of Mechanical Sciences, 34, 299-308.
http://dx.doi.org/10.1016/0020-7403(92)90037-H - 12. Klein, B. (1955) Vibration of Simply Supported Isosceles Trapezoidal Flat Plates. Journal of the Acoustical Society of America, 27, 1059-1060.
http://dx.doi.org/10.1121/1.1908116 - 13. Qatu, M.S. (1994) Vibrations of Laminated Composite Completely Free Triangular and Trapezoidal Plates. International Journal of Mechanical Sciences, 36, 797-809.
http://dx.doi.org/10.1016/0020-7403(94)90010-8 - 14. Zamani, M., Fallah, A. and Aghdam, M.M. (2012) Free Vibration Analysis of Moderately Thick Trapezoidal Symmetrically Laminated Plates with Various Combinations of Boundary Conditions. European Journal of Mechanics-A/Solids, 36, 204-212.
http://dx.doi.org/10.1016/j.euromechsol.2012.03.004 - 15. Manna, M.C. (2012) Free Vibration of Tapered Isotropic Rectangular Plates. Journal of Vibration and Control, 18, 76-91.
http://dx.doi.org/10.1177/1077546310396800 - 16. Bhardwaj, N., Gupta, A.P., Choong, K.K., Wang, C.M. and Ohmori, H. (2012) Transverse Vibrations of Clamped and Simply-Supported Circular Plates with Two Dimensional Thickness Variation. Shock and Vibration, 19, 273-285.
http://dx.doi.org/10.1155/2012/132969 - 17. Mirza, S. and Bijlani, M. (1985) Vibration of Triangular Plates of Variable Thickness. Computers and Structures, 21, 1129-1135.
- 18. Gupta, U.S., Lal, R. and Sharma, S. (2007) Vibration of Non-Homogeneous Circular Mindlin Plates with Variable Thickness. Journal of Sound and Vibration, 302, 1-17.
http://dx.doi.org/10.1016/j.jsv.2006.07.005 - 19. Narita, Y., Maruyama, K. and Sonoda, M. (1981) Transverse Vibration of Clamped Trapezoidal Plates Having Rectangular Orthotropy. Journal of Sound and Vibration, 77, 345-356.
http://dx.doi.org/10.1016/S0022-460X(81)80171-X - 20. Zhou L. and Zheng W.X. (2008) Vibration of Skew Plates by the MLS-Ritz Method. International Journal of Mechanical Sciences, 50, 1133-1141.
http://dx.doi.org/10.1016/j.ijmecsci.2008.05.002 - 21. Quintana, M.V. and Nallim, L.G. (2010) A Variational Approach to Free Vibration Analysis of Shear Deformable Polygonal Plates with Variable Thickness. Applied Acoustics, 71, 393-401.
http://dx.doi.org/10.1016/j.apacoust.2009.12.002 - 22. Korobko, A.V. and Chernyaev, A.A. (2013) Determination of Maximum Deflection in Transverse Bending of Parallelogram Plates Using the Conformal Radiuses Ratio. Russian Aeronautics, 56, 131-134.
http://dx.doi.org/10.3103/S1068799813020049 - 23. Nowacki, W. (1962) Thermo Elasticity. Pergamon Press, New York.



























