Journal of Applied Mathematics and Physics
Vol.04 No.08(2016), Article ID:70158,13 pages
10.4236/jamp.2016.48172
Razumikhin-Type Theorems on General Decay Stability of Impulsive Stochastic Functional Differential Systems with Markovian Switching
Zhiyu Zhan, Caixia Gao
School of Mathematical Sciences, Inner Mongolia University, Hohhot, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 July 2016; accepted 26 August 2016; published 29 August 2016
ABSTRACT
In this paper, the Razumikhin approach is applied to the study of both p-th moment and almost sure stability on a general decay for a class of impulsive stochastic functional differential systems with Markovian switching. Based on the Lyapunov-Razumikhin methods, some sufficient conditions are derived to check the stability of impulsive stochastic functional differential systems with Markovian switching. One numerical example is provided to demonstrate the effectiveness of the results.
Keywords:
Impulsive Stochastic Functional Differential System, p-th Moment Stability, Almost Sure Stability, Lyapunov-Razumikhin Approach

1. Introduction
Impulsive stochastic systems with Markovian switching is a class of hybrid dynamical systems, which is composed of both the logical switching rule of continuous-time finite-state Markovian process and the state represented by a stochastic differential system [1] . Because of the presence of both continuous dynamics and discrete events, these types of models are capable of describing many practical systems in many areas, including social science, physical science, finance, control engineering, mechanical and industry. So this kind of systems have received much attention, recently (for instance, see [2] - [5] ).
It is well-known that stability is the major issue in the study of control theory, one of the most important techniques applied in the investigation of stability for various classes of stochastic differential systems is based on a stochastic version of the Lyapunov direct method. However, the so-called Razumikhin technique combined with Lyapunov functions has also been a powerful and effective method in the study of stability. Recalled that Razumikhin developed this technique to study the stability of deterministic systems with delay in [6] [7] , then, Mao extended this technique to stochastic functional differential systems [8] . This technique has become very popular in recent years since it is extensively applied to investigate many phenomena in physics, biology, finance, etc.
Mao incorporated the Razumikhin approach in stochastic functional differential equations [9] and in neutral stochastic functional differential equations [10] to investigate both p-th moment and almost sure exponential stability of these systems (see also [11] - [13] , for instance). Later, this technique was appropriately developed and extended to some other stochastic functional differential systems, especially important in applications, such as stochastic functional differential systems with infinite delay [14] - [16] , hybrid stochastic delay interval systems [17] and impulsive stochastic delay differential systems [18] - [20] . Recently, some researchers have introduced y-type function and extended the stability results to the general decay stability, including the exponential stability as a special case in [21] - [23] , which has a wide applicability.
In the above cited papers, both the p-th moment and almost sure stability on a general decay are investigated, but mostly used in stochastic differential equations. And As far as I know, a little work has been done on the impulsive stochastic differential equations or systems. In this paper, we will close this gap by extending the general decay stability to the impulsive stochastic differential systems. To the best of our knowledge, there are no results based on the general decay stability of impulsive stochastic delay differential systems with Markovian switching. And the main aim of the present paper is attempt to investigate the p-th moment and almost sure stability on a general decay of impulsive stochastic delay differential systems with Markovian switching. Since the delay phenomenon and the Markovian switching exists among impulsive stochastic systems, the whole systems become more complex and may oscillate or be not stable, we introduce Razumikhin-type theorems and Lyapunov methods to give the conditions that make the systems stable. By the aid of Lyapunov-Razumikhin approach, we obtain the p-th moment general decay stability of impulsive stochastic delay differential systems with Markovian. In order to establish the criterion on almost surely general decay stability of impulsive stochastic delay differential systems with Markovian, the Holder inequality, Burkholder-Davis-Gundy inequality and Borel- Cantelli’s lemma are utilized in this paper.
The paper is organized as follows. Firstly, the problem formulations, definitions of general dacay stability and some lemmas are given in Section 2. In Section 3, the main results on p-th moment and almost sure stability on a general decay of impulsive stochastic delay differential systems with Markovian switching are obtained with Lyapunov-Razumikhin methods. An example is presented to illustrate the main results in Section 4. In the last section the conclusions are given.
2. Preliminaries
Throughout this paper, let 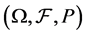 be a complete probability space with some filtration
be a complete probability space with some filtration 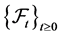 satisfying the usual condition (i.e., the filtration is increasing and right continuous while
satisfying the usual condition (i.e., the filtration is increasing and right continuous while 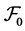 contain all P-null sets). Let
contain all P-null sets). Let  be an m-dimensional
be an m-dimensional  -adapted Brownian motion.
-adapted Brownian motion.
Let 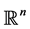 be the n-dimensional Euclidean space;
be the n-dimensional Euclidean space; 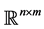 denotes the
denotes the 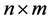 real matrix space;
real matrix space; 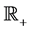 is the set of all non-negative real numbers;
is the set of all non-negative real numbers;  denotes the family of continuous functions
denotes the family of continuous functions 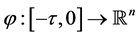 with the norm
with the norm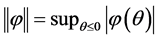 ;
;  denotes the standard Euclidean norm for vectors; let
denotes the standard Euclidean norm for vectors; let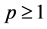 ,
, 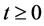 ,
,









Let



where




We assume that the Markov chain 







In this paper, we consider the following impulsive stochastic delay differential systems with Markovian switching

where the initial value 

represents the impulsive perturbation of x at time




For the existence and uniqueness of the solution we impose a hypothesis:
Assumption (H): For 


For all


For all

Definition 1 
(1) It is continuous, monotone increasing and differentiable;
(2) 

(3)
(4) for any
Definition 2 For





when



Definition 3 impulsive stochastic delay differential systems with Markovian switching (1) is said to be almost surely stable with decay 




when

Let 




where
Lemma 1 (Burkholder-Davis-Cundy inequality) Let



where
Lemma 2 (Borel-Cantelli’s lemma)
(1) If 

That is, there exist a set 





(2) If the sequence 

That is, there exists a set 





3. Main Results
In this section, we shall establish some criteria on the p-th moment exponential stability and almost exponential stability for system (1) by using the Razumikhin technique and Lyapunov functions.
Theorem 1 For systems (1), let (H) hold, and 



(H1) For all

(H2) For all

For all 


where
(H3) For all 

where 

Then, for any initial




Proof. Fix the initial data 








Then it follows from condition (H1) that
In the following, we will use the mathematical induction method to show that

In order to do so, we first prove that

This can be verified by a contradiction. Hence, suppose that inequality (9) is not true, than there exist some 



the interval



Define



Consequently, for all
And so
By condition (H2) we have
Consequently,

Applying the 


By condition (14), we obtain

On the other hand, a direct computation yields
that is
which is a contradiction. So inequality (9) holds and (8) is true for



Then, we will prove that (8) holds for

Suppose (18) is not true, i.e. there exist some 

Then, it follows from the condition (H3) and (17) that
which implies that the 


interval



Define



Fix any


If 




Therefore,
by condition (H2) we have
Consequently,

Similar to (15), applying the 

By condition (25), we obtain
On the other hand, by (20) and (22), we have
that is
which is a contradiction. So inequality (18) holds. Therefore, by mathematical induction, we obtain (8) holds for all
which implies
i.e., system (1) is pth moment exponentially stable with decay 

Theorem 2 For system (1), suppose all of the conditions of Theorem 1 are satisfied. Let




Then, for any initial 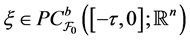






Proof. Fix the initial data 


where
Choose 



is the maximum integer not more than x. Then for any





For each i when


By Theorem 1, we have

By Holder inequality, condition (26) and Theorem 1, we derives that

Similarly, by the Lemma 1 and (32), we obtain

where 
Substituting (31), (32) and (33) into (30) yields

Thus, it follows from (29) and (34), we obtain
Using Chebyshev inequality, we have
Since


That is
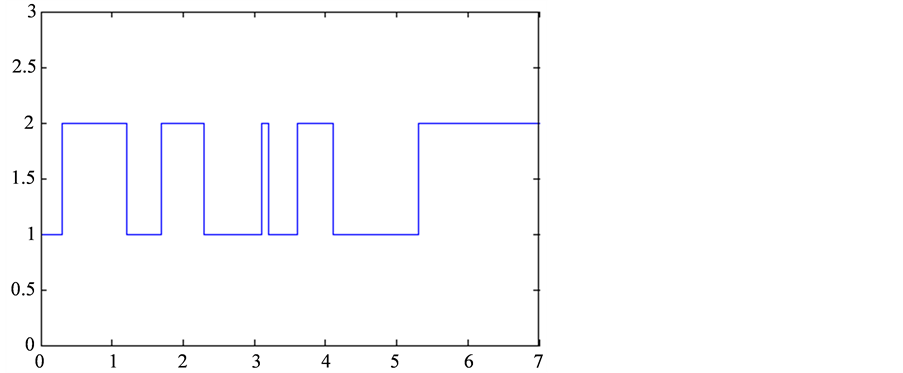
Figure 1. State of the example.
Figure 2. Markovian switching of the example.
Thus, the system (1) is almost surely stable with decay 

4. Examples
In this section, a numerical example is given to illustrate the effectiveness of the main results established in Section 3 as follows. Consider an impulsive stochastic delay system with Markovian switching as follows

where 

And independent of the scalar Brownian motion





Choosing






and
By Theorem 1, we know that

5. Conclusion
In this paper, p-th moment and almost surely stability on a general decay have been investigated for a class of impulsive stochastic delay systems with Markovian switching. Some sufficient conditions have been derived to check the stability criteria by using the Lyapunov-Razumikhin methods. A numerical example is provided to verify the effectiveness of the main results.
Acknowledgements
The work was supported by the National Natural Science Foundation of China under Grant 11261033, and the Postgraduate Scientific Research Innovation Foundation of Inner Mongolia under Grant 1402020201336.
Cite this paper
Zhiyu Zhan,Caixia Gao, (2016) Razumikhin-Type Theorems on General Decay Stability of Impulsive Stochastic Functional Differential Systems with Markovian Switching. Journal of Applied Mathematics and Physics,04,1617-1629. doi: 10.4236/jamp.2016.48172
References
- 1. Ji, Y. and Chizeck, H. (1990) Controllability, Stabilizability and Continuous Time Markovian Jump Linear Quadratic Control. IEEE Transactions on Automatic Control, 35, 777-788.
http://dx.doi.org/10.1109/9.57016 - 2. Liu, Z. and Peng, J. (2009) p-Moment Stability of Stochastic Nonlinear Delay Systems with Impulsive Jump and Markovian Switching. Stochastic Analysis and Applications, 27, 911-923.
http://dx.doi.org/10.1080/07362990903136439 - 3. Dong, Y., Wang, Q. and Sun, J. (2009) Guaranteed Cost Control for a Class of Uncertain Stochastic Impulsive Systems with Markovian Switching. Stochastic Analysis and Applications, 27, 1174-1190.
http://dx.doi.org/10.1080/07362990903259421 - 4. Sathananthan, S., Jameson, N., Lyatuu, I. and Keel, L.H. (2012) Hybrid Impulsive State Feedback Control of Markovian Switching Linear Stochastic Systems. Communications in Applied Analysis, 16, 665-686.
- 5. Sathananthan, S., Jameson, N., Lyatuu, I. and Keel, L.H. (2013) Hybrid Impulsive Control of Stochastic Systems with Multiplicative Noise under Markovian Switching. Stochastic Analysis and Applications, 31, 894-911.
http://dx.doi.org/10.1080/07362994.2013.817254 - 6. Razumikhin, B.S. (1956) On the Stability of Systems with Delay. Prikl. Mat. Mekh, 20, 500-512.
- 7. Razumikhin, B.S. (1960) Application of Lyapunov’s Method to Problems in the Stability of Systems with a Delay. Automat, i Telemekh, 21, 740-749.
- 8. Mao, X. (1997) Stochastic Differential Equations and Applications. Horwood Publications, Chichester.
- 9. Mao, X. (1996) Razumikhin-Type Theorems on Exponential Stability of Stochastic Functional Differential Equations. Stochastic Processes and their Applications, 65, 233-250.
http://dx.doi.org/10.1016/S0304-4149(96)00109-3 - 10. Mao, X. (1997) Razumikhin-Type Theorems on Exponential Stability of Neutral Stochastic Functional Differential Equations. SIAM Journal on Mathematical Analysis, 28, 389-401.
http://dx.doi.org/10.1137/S0036141095290835 - 11. Shsikhet, L. (2013) Lyapunov Functionals and Stability of Stochastic Functional Differential Equations. Springer International Publishing, Switzerland.
http://dx.doi.org/10.1007/978-3-319-00101-2 - 12. Kloeden, P.E. and Platen, E. (1992) Numerical Solution of Stochastic Differential Equations. Springer-Verlag, Berlin Heidelberg.
- 13. Huang, L. and Deng, F. (2009) Razumikhin-Type Theorems on Stability of Stochastic Retarded Systems. International Journal of Systems Science, 40, 73-80.
http://dx.doi.org/10.1080/00207720802145478 - 14. Yang, Z., Zhu, E., Xu, Y., et al. (2010) Razumikhin-Type Theo-rems on Exponential Stability of Stochastic Functional Differential Equations with Infinite Delay. Acta Applicandae Mathe-maticae, 111, 219-231.
http://dx.doi.org/10.1007/s10440-009-9542-1 - 15. Pavlovic, G. and Jankovic, S. (2012) Razumikhin-Type Theorems on General Decay Stability of Stochastic Functional Differential Equations with Infinite Delay. Journal of Computational and Applied Mathematics, 236, 1679-1690.
http://dx.doi.org/10.1016/j.cam.2011.09.045 - 16. Wei, F. and Wang, K. (2007) The Existence and Uniqueness of the Solution for Stochastic Functional Differential Equations with Infinite Delay. Journal of Mathematical Analysis and Applications, 331, 516-531.
http://dx.doi.org/10.1016/j.jmaa.2006.09.020 - 17. Mao, X., Lam, J., Xu, S. and Gao, H. (2006) Razumikhin Method and Exponential Stability of Hybrid Stochastic Delay Interval Systems. Journal of Mathematical Analysis and Applications, 314, 45-66.
http://dx.doi.org/10.1016/j.jmaa.2005.03.056 - 18. Cheng, P. and Deng, F. (2010) Global Exponential Stability of Impulsive Stochastic Functional Differential Systems. Statistics and Probability Letters, 80, 1854-1862.
http://dx.doi.org/10.1016/j.spl.2010.08.011 - 19. Wu, X., Zhang, W. and Tang, Y. (2013) Pth Moment Stability of Impulsive Stochastic Delay Differential Systems with Markovian Switching. Communications in Nonlinear Science and Numerical Simulation, 18, 1870-1879.
http://dx.doi.org/10.1016/j.cnsns.2012.12.001 - 20. Peng, S. and Jia, B. (2010) Some Criteria on pth Moment Stability of Impulsive Stochastic Functional Differential Equations. Statistics and Probability Letters, 80, 1085-1092.
http://dx.doi.org/10.1016/j.spl.2010.03.002 - 21. Hu, S., Huang, C. and Wu, F. (2008) Stochastic Differential Equations. Science Press, Beijing.
- 22. Wu, F. and Hu, S. (2012) Razumikhin-Type Theorems on General Decay Stability and Robustness for Stochastic Functional Differential Equations. International Journal of Robust and Nonlinear Control, 22, 763-777.
http://dx.doi.org/10.1002/rnc.1726 - 23. Pavlovic, G. and Jankovic, S. (2012) Razumikhin-Type Theorems on General Decay Stability of Stochastic Functional Differential Equations with Infinite Delay. Journal of Computational and Applied Mathematics, 236, 1679-1690.
http://dx.doi.org/10.1016/j.cam.2011.09.045