Journal of Applied Mathematics and Physics
Vol.04 No.07(2016), Article ID:69247,7 pages
10.4236/jamp.2016.47146
Solving the Burgers-Huxley Equation by G'/G Expansion Method
Mingxing Zhu
School of Humanities and Sciences, Jiangsu University of Science and Technology, Zhangjiagang, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 May 2016; accepted 25 July 2016; published 28 July 2016
ABSTRACT
By introducing and extending the G'/G expansion method with the aid of computer algebraic system “Mathematics”, the exact general solutions were obtained for the Burgers-Huxley equation and special form. Final results were represented in hyperbolic function, trigonometric function and rational function with arbitrary parameters.
Keywords:
Burgers-Huxley Equation Exact Solution Mathematics

1. Introduction
For the Burgers-Huxley equation
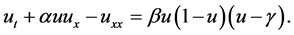 (1)
(1)
This an important equation used to describe the nonlinear diffusion phenomenon. In recent years, with the development of Symbolic Computation System and its perfection, people put forward a number of methods for solving the nonlinear equations of mathematical physics, such as the homogeneous balance method, F-method, Tanh method, projective Riccati method, ADM method [1] - [4] and bifurcation theory to direct integral method [5] and so on. G'/G expansion method [6] is proposed for solving nonlinear evolution equation and provided an effective method. This method has effectively solved many nonlinear evolution equations.
This article will make the G'/G expansion method extended further, solving the Burger-Huxley equation [7] - [10] and two kinds of special transformations.
2. The Introduction of Extended G'/G-Expansion Method [11] [12]
Given nonlinear PDE, containing two independent variables x and t:
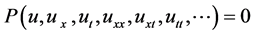 (2)
(2)
Among them, P is the polynomial of variable element u with high order partial derivative term and nonlinear term. For equations by G'/G expansion method (2) comprises the following steps:
1) On Equation (2) traveling wave reduction, let
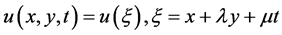 (3)
(3)
Among them, 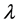 and
and 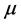 are undetermined constants. Equation (3) is plugged into Equation (2). (ODE type):
are undetermined constants. Equation (3) is plugged into Equation (2). (ODE type):
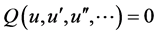 (4)
(4)
2) The 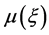 can be expressed as the finite series of G'/G
can be expressed as the finite series of G'/G
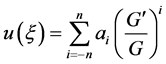 (5)
(5)
The 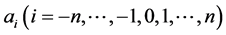 is a undetermined constant; the
is a undetermined constant; the 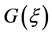 meet the two order linear ordinary differential equation as follows
meet the two order linear ordinary differential equation as follows
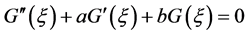 (6)
(6)
The positive integer n can be determined by the balance principle homogeneous.
3) We will plug Equation (5) into Equation (4), then the left of Equation (4) translates the polynomial of G'/G, making this polynomial coefficients are all zero, can obtain the algebraic equations about
 .
.
4) With the help of Mathematica, we can solve the algebraic equations. so we can obtain the exact traveling wave solutions of Equation (1) that plugging the resulting value of 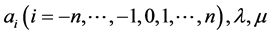 into Equation (4) [13] [14] .
into Equation (4) [13] [14] .
3. Calculate the Exact Solution of the Burger-Huxley Equation [15]
Make Burger-Huxley Equation for wave reduction, let
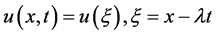 (7)
(7)
so Equation (1) can translate the ODE equation;
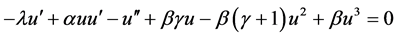 (8)
(8)
We can obtain a series of expansion of n is 1, assuming Equation (8) has the following form solution:

Among them, 

In Equation (9) and Equation (10), 

Plugging Equation (11) into Equation (8), Equation (8) can be transformed into a polynomial about G'/G expansion. Merger these items with respect to G'/G expansion which have the same power, and its coefficient is zero. We can obtain the equations as follows.

If set 

1)
2)


By using mathematics software to calculate again, a general solution of Equation (10) can be represented as:

Substituting Equation (13) and Equation (14) into Equation (9), traveling wave solution of Equation (1) can be obtained:
1) When
where
2) When
where
3) When
where
When the original equation of the parameters in the 
Case 1: when

We assume that the same G'/G expression, by substitution to Equation (15) to obtain the following equations:

With the aid of Mathematica software, we can get the value of 
1)
2)
3)

Equation (15) can be expressed as the solution:
1) When
where
2) When
where
3) When
where
Case 2: when

Make the equation to traveling wave reduced, let

Make Equation (19) to integral, so

We assume that the same G'/G expression, through to obtain the following equations

With the aid of mathematica software, obtain the solution of the following:


so the solution of Equation (18) can be expressed:

Including to Equation (15), we can obtain the accurate solution of Equation (18):
1) When
where
2) When
where
3) When
where
4. Conclusion
Based on the homogeneous balance method, the article obtains solutions of the Burgers-Huxley equation and two kinds of transformation type by the G'/G expansion method, making the Burgers-Huxley equation and its derivative equation solution in the form of more abundant. At the same time, we can obtain the hyperbolic traveling wave solutions of the equation and find the G'/G expansion method [16] in solving nonlinear evolution equations has very extensive practical value.
Cite this paper
Mingxing Zhu, (2016) Solving the Burgers-Huxley Equation by G'/G Expansion Method. Journal of Applied Mathematics and Physics,04,1371-1377. doi: 10.4236/jamp.2016.47146
References
- 1. Yan, Z.Y. (2007) The Structure of the Complex Nonlinear Wave Theory and Its Applications. Science Press.
- 2. Guo, Y.C. (2008) An Introduction to Nonlinear Partial Differential Equation. Tsinghua University Press, Beijing.
- 3. Lou, S.Y. and Tang, X.Y. (2006) Nonlinear Mathematical Physics Method. Science Press.
- 4. Zhang, W.M. (2009) A Number of Solving Nonlinear Wave Equation of Structural Research. PhD Thesis of Jiangsu University, Zhenjiang.
- 5. Wang, M.L., Li, Z.B. and Zhou, Y.B. (1999) The Homogeneous Balance Principle and Its Application. Journal of Lanzhou University, 35, 8-16.
- 6. Han, B.B. (2010) Promotion (G’/G) Expansion Method of Solving Nonlinear Equation. Journal of Chifeng Institute, 26, No. 5.
- 7. Wang, Q.L. and Deng, X.J. (2010) Solution and Its Branches for a Class of Generalized Burgers-Huxley Equation. The Practice of Mathematics and Understanding, 40, No. 1.
- 8. Liu, X.Y., Jiang, L. and Guo, Y.C. (2006) New Exact Solutions of Burgers-Huxley Equation. Journal of Shandong University of Science and Technology, 20, No. 5.
- 9. Gao, Z.B. (2008) Exact Solutions of Burgers-Huxley Equations. Master Degree Theses of Master of Jiangsu University, Zhenjiang.
- 10. Sun, X.X. and Xu, Y.J. (2009) Several Trigonometric Function Solution of the Generalized Variable Coefficient Burgers-Huxley Equations. Journal of Changshu Institute of Technology, 8, 24-29.
- 11. Wang, M.L., Li, X.Z. and Zhang, J.L. (2008) The (G’/G)-Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423.
http://dx.doi.org/10.1016/j.physleta.2007.07.051 - 12. Zhu, M.X., Wu, L., Yin, C.C. and Zhang, M.Y. (2011) Solving (2 + 1)-Dimensional Davey-Stewartson Equation by (G’/G) Expansion Method. International Journal of Nonlinear Science, 12, 2.
- 13. Yang, Z.J. (1994) Travelling Wave Solutions to Nonlinear Evolution and Wave Equations. Journal of Physics A: Mathematical and General, 27, 2837-2855.
http://dx.doi.org/10.1088/0305-4470/27/8/021 - 14. Lu, B.Q., Xiu, B.Z., Pang, Z.L. and Jiang, X.F. (1993) Exact Travelling Wave Solution of One Class of Nonlinear Diffusion Equation. Physics Letters A, 175, 113-115.
http://dx.doi.org/10.1016/0375-9601(93)90131-I - 15. Deng, X.J. (2008) Travelling Wave Solutions for the Generalized Burgers-Huxley Equation. Applied Mathematics and Computation, 204, 733-737.
http://dx.doi.org/10.1016/j.amc.2008.07.020 - 16. Zhang, S., Dong, L., Ba, J.-M. and Sun, Y.-N. (2009) The (G’/G)-Expansion Method for Nonlinear Differential-Difference Equations. Physics Letters A, 373, 905-910.
http://dx.doi.org/10.1016/j.physleta.2009.01.018


























