Received 18 March 2016; accepted 27 May 2016; published 30 May 2016

ABSTRACT

In the first part of this paper, we found a more convenient algorithm for solving the equation of motion of a system of n bodies. This algorithm consists in solving first the trajectory equation and then the temporal equation. In this occasion, we will introduce a new way to solve the temporal equation by curving the horizontal axis (the time axis). In this way, we will be able to see the period of some periodic systems as the length of a certain curve and this will allow us to approximate the period in a different way. We will also be able to solve some problems like the pendulum one without using elliptic integrals. Finally, we will solve Kepler’s problem using all the formalism.

Keywords:

Classical Mechanics, Pendulum, Kepler’s Problem

1. Introduction

We shall use the following notation given at the first part [1] .

///

Notation: Along this paper, we shall consider the variables t and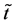. The derivatives respect to the variable t will be denoted by the symbol “・” while the derivatives respect the variable 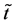will be denoted by the symbol apostrophe “'”. In addition, if 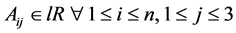we will denote:

・

・

・

・

・

///

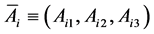
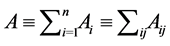
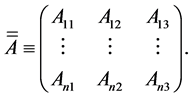
In the first part of this paper, we study the problem of n bodies interacting in a certain medium, which we will assume that it is the vacuum in this part (since the general case is analogous), whose equation of motion (in the vacuum case) is given by

(1)

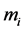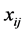where and are the mass and the component j of the position of the i-body respectively while is the force applied to the i-body.

We saw that if 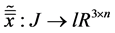is such that 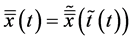with

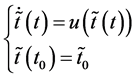(2)

then Equation (1) (without the initial conditions) is equivalent to

(3)

where

(4)

(5)

. (6)

At the same time, we saw that Equation (3) and the initial conditions (and hence Equation (1)) are equivalent to

(7)

(8)

(9)

(10)

where h can be any function, i, j, l and m are arbitrary indexes satisfying, and is given by

. (11)

We also proved that if is a parametrization of C, where C is the image of, then it satisfies conditions (7), (8) and (9). Due to this fact, we call trajectory equation to condition (7), since C represents the trajectory of the system and conditions (8), (9) are just extra conditions for particular cases. We finally saw that if satisfies conditions (7), (8) and (9), then given by also satisfies them, with such that and. In addition

. (12)

On the other hand, we call temporal equation to Equation (2), since it determines the relationship between t and. We also call temporal equation to Equation (10). We proved that if the force comes from a potential V, then we can write Equation (10) (for) using the mechanical energy of the system as follows

(13)

where E is the energy.

Based on these results, we develop the following algorithm for solving Equation (1):

1) Find a solution of the trajectory equation and check that it satisfies conditions (8) and (9).

2) Choose conveniently a function with and in order to build another solution given by.

3) Find the function u given in Equation (10) (or (13)).

4) Solve the temporal equation.

Finally, is the solution of Equation (1).

We saw that if we want to solve the equation of motion, it is more convenient to follow this algorithm.

In this occasion, we will change the last step of this algorithm, i.e., we will find a new way to solve the temporal equation, by curving the horizontal axis (the time axis). In this way we will be able to solve some problems that cannot be solved in the traditional way (without using elliptic integrals) like the pendulum problem. We will also be able to see the period of some periodic systems as the length of a curve. This fact can be compared with the Hamilton-Lagrange’s formalism, where we can see the period of some systems as the area of a surface given by the phase space [2] .

First, we will use the arc length function and its inverse in order to introduce a new way to graph functions by curving the axes. Then, we will use these results in order to complete the algorithm and to graph each component of the solution of Equation (1) in this way. Finally, we will solve the harmonic oscillator, the pendulum, the particle under the action of two elastic springs [3] and Kepler’s problems using all the formalism.

2. A New Way to Graph Functions by Curving the Axes

In this section we will use the arc length function and its inverse in order to introduce a new way to graph functions by curving the axes. Before doing this, we will introduce the notation that will be used and we will give some definitions.

///

Notation and preliminaries: let C be a curve in the plane given by a parametrization with.

・ We will denote by and, i.e., is the image of and is the image of.

・ We will assume that and we will denote by.

・ If and are the lengths of the curve from to and respectively, we write.

Definition 1: let C be a curve in the plane describing the graph of a function depending of x and given by a parametrization. We define the function as follows: if and only if s is either or, where l is the length of the curve C measured from to and the sign depends of the orientation of the parametrization as shown in Figure 1 and Figure 2.

In a similar way, if C describes the graph of a function depending of y, we define the function as shown in Figure 3 and Figure 4.

Definition 2: let C be a curve in the plane given by a parametrization. We define the function as follows: if and only if s is either or, where l is the length of the curve C measured from to and the sign depends of the orientation of the parametrization as shown in Figure 5 and Figure 6.

In a similar way, we define the function as shown in Figure 7 and Figure 8.

///

Before proceeding to the new way to graph functions, we will discuss some points about these functions.

On the one hand, note that all these functions are uniquely determined by the curve C described implicitly by, the initial point and the orientation. In addition, there are infinite parametrizations that define the same function. Then, in the examples that we will see later, we will find F, and the orientation in order to determine these functions, i.e., we will not find the parametrization.

On the other hand, if C describes the graph of a function depending of x, by Definition 1 it is

easily proved that is given by

(14)

where the sign + corresponds to the orientation given in Figure 1 and the sign − to the orientation given in Figure 2.

In addition, in this case we can see in Definition 2 that is the inverse function of and then it follows from the inverse function theorem and Equation (14) that is given by

(15)

where the sign + corresponds to the orientation given in Figure 5 and the sign-to the orientation given in Figure 6.

If C describes the graph of a function depending of y the process is analogous by changing and by and.

Next, we will use these functions in order to graph functions by curving the axes.

///

Curvilinear vertical axis: assume we have a differential equation whose solution is given by the function where the curve C is given by, it is oriented as in Figure 3 and (with). Then, we can graph this function as shown in Figure 9.

This way of making the graph of the function is equivalent to make the graph of the function by curving the X-axis with the function x. Note that the origin of the horizontal axis is (i.e. it does not change) while the origin of the vertical axis is. Note also that the original X-axis is not used to make the graph of the function, it is only used to perform the new y-axis and to make the graph of the function. Finally, we can graph X versus t in a more simple way as shown in Figure 10.

If the curve C is oriented as in Figure 4 the direction of the X-axis changes.

Curvilinear horizontal axes: assume now that we have a differential equation whose solution is given by the function where the curve C is given by, it is oriented as in Figure 5 and (with). Then, we can graph this function as shown in Figure 11.

This way of making the graph of the function is equivalent to make the graph of the function by curving the t-axis. Note that the origin of the vertical axis is (i.e. it does not change) while the origin of the horizontal axis is. Note also that the original t-axis is not used to make the graph of the function, it is only used to perform the new t-axis and to make the graph of the function. Like the previous case, we can graph

X versus t in a more simple way as shown in Figure 12.

If the curve C is oriented as in Figure 6 the direction of the X-axis changes.

If C is not the graph of a function the idea is the same. For example if C is a closed curve and it is positively oriented, the graph of X versus t is shown in Figure 13. In this case we need to say how many times the parametrization of the curve “turns”. If it turns indefinitely, then and we can see in Figure 13 that X is a periodic function whose period is given by the length of C.

///

Next, we will complete the algorithm for solving the equation of motion by using these results. We will only

use the functions, since we will just curve the t-axis.

3. A New Way to Solve the Temporal Equation

In the first part of this paper we find a more convenient algorithm for solving the equation of motion of a system of n bodies. In this section we will use the functions in order to change the step four of that algorithm, by solving the temporal equation in a different way.

Before doing that, we will need the following mathematical notion.

///

Definition 3: let and. We define the following set:

Note 1: in order an element x belongs to it is necessary (but not sufficient) that

in order the term which appears under the radical be no negative.

Note 2: if we do not choose the element appropriately (for instance if) then the set can be empty.

Note 3: although, it may be possible that x belongs to, since the improper integral could converge. Analogously, if, it may be possible that the set is not empty for the same reason.

Proposition 1: let and be such that

. (16)

Let also be such that

(17)

where and the sign is arbitrary.

Then, if u does not change the sign in the interval, is the solution of the differential equation where C is described by, , and the curve is oriented as follows

・ If u is positive, then C is oriented as in Figure 5.

・ If u is negative, then C is oriented as in Figure 6.

Proof: by Equation (17) we have

It follows that

where the sign is + provided and the sign is − provided.

Then, according to Equation (15) we have that is the solution of Equation (16) where and C is described by with its respective orientation.

///

By Proposition 1, we will complete the algorithm for solving the equation of motion.

We will assume that the initial time, which implies that Equation (2) is written as Equation (16) by taking. In addition, we can see in Equation (10) (or (13)) that u does not change its sign, and hence we can use Proposition 1. Then, we will change the algorithm as follows

1) Find a solution of the trajectory equation and check that it satisfies conditions (8) and (9).

2) Choose conveniently a function with and in order to build another solution given by.

3) Find the function u given in Equation (10) (or (13)).

4) Find a function y that satisfies Equation (17).

Finally, is the solution of Equation (1) where C is described by, and the curve is oriented as follows

・ If is positive, then C is oriented as in Figure 5.

・ If is negative, then C is oriented as in Figure 6.

where is given by Equation (11).

In this way, we can graph each component of as in Figure 12 (or 13) by curving the horizontal axis, i.e., the time axis.

Note that we have only changed the step four. However, there is also a big difference in the step two.

In the step two of the old algorithm, the statement “choose conveniently a function” refers to choose so that the temporal equation can be solved easily. However, according to Equation (12) we have

This implies that

Hence we arrive to

Then, we can see that choosing so that the temporal equation can be solved easily is equivalent to make a

simple change of variables in the temporal equation. This implies that if the solution of is a non-elemental function, then the solution of will also be a non-elemental function. Hence, we can say that in the old algorithm, the step two is not very important.

In the step two of the new algorithm, the statement “choose conveniently a function” refers to

choose so that, which implies that according to Equation (12), and then

in most cases, and that the integral given in Equation (17) can be solved easily. We will see in the following examples that in this case, the step two is key since if we choose properly, then we will be able to find y analytically and if we do not choose properly, we will not be able to find it.

Finally, suppose that there is just one body and it moves in only one direction and we find a function that satisfies and. Then, the step one is satisfied. In addition, in this case the step two is unnecessary. Hence, the algorithm in this case becomes

1) Choose conveniently a function that satisfies and.

2) Find the function u given in Equation (10) (or (13)).

3) Find a function y that satisfies Equation (17).

As before, the statement “choose conveniently a function “ refers to choose so that and that the integral given in Equation (17) can be solved easily.

Finally, suppose that the universe is only composed of the n bodies. Then, it would be impossible to tell if the bodies move according to and the time t is “an horizontal line” or if the bodies move according to and the time curves according to Equation (17).

Hence, we can say that the master equation is a generalization of Newton’s second law which includes the possibility that the time curves. We can also say that we do not know if Newton’s second law is all right since we do not know if the time curves or does not.

Next we will see four examples. The first three examples will be one dimensional problems and then we will use this last algorithm.

4. Examples

In this section, we will solve the harmonic oscillator, the pendulum, the particle under the action of two elastic springs [2] and Kepler’s problems. Note that all these problems have periodic solutions (at least for some values of the energy). We will use this formalism in order to approximate the periods. In order to do that we will need the following proposition.

///

Proposition 2: let C be a curve with elliptical shape with semi-axes a and b and let and be two curves as shown in Figure 14. Then we have

where, and are the length of C, and respectively.

///

Suppose that is the solution of one of these problems with C a closed curve with elliptical shape and semi-axes a and b and. If turns indefinitely the solution holds for all t and according to Figure 13 it is periodic. The period is given by the length of C and then, according to this proposition, we have

where is the period.

In other words, where

(18)

. (19)

Hence, if we know a and b, we can approximate the period of the solution using Equation (18) and the error of the approximation is given by Equation (19). If we call to the ratio between the semi-minor axis and the semi-major axis, according to Equations (18) and (19), the relative error is given by

. (20)

Since, then it is easily proved that

(21)

where.

In addition, if is the equilibrium point, we can also calculate the amplitude of the motion by doing

. (22)

Next we will see some examples and we will use these results in order to approximate the period of the solution. In all the examples we will consider just one body and we will denote by and. In the one dimensional examples we will use the second algorithm.

4.1. Harmonic Oscillator

The force and the potential in this case are given by

(23)

where k is the elastic constant.

Before proceeding, we will call

. (24)

We propose as a solution the following one

(25)

where v is given by

(26)

with E the mechanical energy.

We will choose

. (27)

Then, the solution satisfies (since we are not considering the trivial case) and and hence the first step of the algorithm is complete.

In order to find u, according to Equations (5), (23), (24), (25) and (26) we have

(28)

. (29)

In addition, according to Equations (11) and (25),

Since v is positive, then

. (30)

Finally, by Equations (13), (28), (29) and (30) the function u is given by

. (31)

Then, the second step of the algorithm is complete.

In order to find y, according to Equation (31) we have

Then, by making the change of variable

and choosing conveniently the value of, Equation (17) becomes

Without being quite formal, it follows that the curve C is given by

. (32)

Hence, the third step is complete.

Finally, is the solution where is given by Equation (25), C is described by Equation (32), with given in Equation (27) and the orientation is given according to the sign of the initial velocity.

Since C is a closed curve and we are considering that turns indefinitely, we can graph X versus t as given

in Figure 13. The solution is periodic and in this case, since the curve is a circumference of ratio, we can calculate the period analytically and it is given by

. (33)

In addition, according to Equations (22), (24), (25) and (26) the amplitude is given by

We can find the period and the amplitude in the traditional way and we obtain the same results.

4.2. The Pendulum

We will call to the angle formed by the rope and the vertical and we will denote

(34)

where l is the length of the rope.

Then, the equation of motion can be written as Equation (1) where the force is given by

and g is the gravity.

We will choose conveniently the potential as follows

. (35)

Before proceeding, using this equation and the fact that the kinetic energy is positive, note that

. (36)

In addition, we will define conveniently

(37)

. (38)

We propose the solution of Equation (25) and we will take according to Equation (27) where in this case

. (39)

By condition (36) we can see that v is well defined.

As in the harmonic oscillator example, the solution satisfies and which implies that the first step of the algorithm is complete.

In order to find u, according to Equations (5), (25), (35) and (39) we have

(40)

. (41)

In addition, in a similar way we can prove Equation (32).

Finally, according to Equations (13), (32), (40) and (41) the function u is given by

. (42)

Then, the second step of the algorithm is complete.

In order to find y, according to Equation (42) we have

Then, by making the change of variable

and choosing conveniently the value of, Equation (17) becomes

Without being quite formal, it follows that the curve C is given by

According to Equation (39) we can also write C as follows

(43)

Hence, the third step is complete.

Finally, is the solution where is given by Equation (25), C is described by Equation (43), with given in Equation (27) and the orientation is given according to the sign of the initial velocity. In addition, according to Equation (34) we have

If, then C is a closed curve with elliptical shape. The semi-axes of the ellipse are given by

(44)

. (45)

It is easily proved that and hence the “ellipse is vertical”.

Since C is a closed curve and we are considering that turns indefinitely, we can graph X versus t as in Figure 13. The solution is periodic and according to Equations (18), (44) and (45) its approximate period is given by

. (46)

The relative error is given by Equation (20) where in this case

. (47)

We will study the limit cases, i.e., when (see Equation (36)) and when.

The first case corresponds to small oscillations and according to Equation (38). Then, by Equation (47) it is easily proved that which implies that the curve is a circumference. Hence, as in the harmonic oscillator case, it is not necessary to approximate the period, since it can be calculated analytically. According to

Equations (44) and (45) we have that and then the ratio of the circumference takes the value of. Hence, the period is given by Equation (33) where in this case is given by Equation (37) as was expected.

In the second case we have that and then, Equations (46) and (47) becomes

Since we can see in Equation (20) that

Taking into account that in the previous case and then, according to Equations (20) and (21), the relative error is maximum, we can say that to higher energy, better approximation in the period. However, by Equations (19), (44) and (45) it is easily proved that the error depending on is a decreasing function and it tends to infinity when.

Finally, we can also find the amplitude and according to Equations (22), (25), (39) and (44) it is given by

We can find the amplitude in the traditional way and see that we arrive to the same result.

If the graph of the curve is shown in Figure 15 where a is given by

If we graph X versus t as in Figure 12 and we assume that the initial velocity is positive we can see that the solution is increasing and since the curve has vertical asymptotes in, according to Equations (25) and (39) it tends to

However, it never reaches that value.

If the graph of the curve is shown in Figure 16 where a and b are given by

(48)

. (49)

In this case, if we graph X versus t as in Figure 12 and we assume that the initial velocity is positive, we can see that X increases indefinitely and hence according to Equation (34) increases too. This means that the pendulum

describes a rotating circular motion. The time that takes to the pendulum to circle is given by the length of

the curve from to, since according to Equations (25), (27) and (34)

As in Proposition 2, we can obtain lower bounds and upper bounds for this length and approximate in the same way as before. For example if, taking into account that according to Equations (27), (39) and (48)

it is easily proved that where

with a and b given by Equations (48) and (49).

4.3. Particle under the Action of Two Elastic Springs

The force and the potential in this case, considering small oscillations, are given by [2]

(50)

where k is the elastic constant and is the natural length of the springs.

We propose as a solution

(51)

where

(52)

(53)

with given in Equation (24) and E the mechanical energy.

We will choose

. (54)

Then, the solution satisfies (since we are not considering the trivial case), and hence the first step of the algorithm is complete.

In order to find u, according to Equations (5), (50), (51), (52) and (53) we have

(55)

. (56)

In addition, according to Equations (11) and (51),

Since A, and are positive, then Equation (30) holds.

Finally, according to Equations (13), (30), (55) and (56) the function u is given by

. (57)

Then, the second step of the algorithm is complete.

In order to find y, according to Equation (57) we have

Then, by making the change of variable

and choosing conveniently the value of, Equation (17) becomes

Without being quite formal, it follows that the curve C is given by

Using well known properties of the trigonometric and the hyperbolic functions we can write this equation as follows

. (58)

Hence, the third step is complete.

Finally, is the solution where is given by Equation (51), C is described by Equation (58), with given in Equation (54) and the orientation is given according to the sign of the initial velocity.

It is proved that C is a closed curve with elliptical shape. The semi-axes a and b are given by

(59)

. (60)

In this case and hence the “ellipse is horizontal”.

Since C is a closed curve and we are considering that turns indefinitely, we can graph X versus t as in Figure 13. The solution is periodic and according to Equations (18), (58) and (59) its approximate period is given by

. (61)

The relative error, according to Equation (20) and taking into account that

is given by

Note that if (which implies small oscillations), then (see Equation (53)) and hence. On the other hand, if, then and hence.

By means of the procedure indicated before, it is easily proved that A is the amplitude.

4.4. Kepler’s Problem

The force and the potential in this case are given by

(62)

(63)

where, and is a constant.

We will assume that the initial conditions are given by

(64)

where and are positive.

In addition, we will choose.

Then, since is a base of the orthogonal subspace (see the appendix of [1] ) and (because), the trajectory equation becomes

(65)

where according to Equations (4), (6) and (62)

(66)

(67)

. (68)

We propose the following solution

(69)

where, are real constants and, w can be complex.

We have

Let

(70)

then we arrive to

In order to solve the integrals given in Equation (67) and (68), we will ask that this expression is a perfect square. It happens if and only if

(71)

where we assume that, provided is real.

In this case we obtain

We will assume that

(72)

and hence we finally arrive to

. (73)

On the other hand, according to Equation (69) we have

. (74)

Then, by Equation (69) it follows that

We can write these expressions using Equation (70) as follows

(75)

. (76)

Hence, by Equations (73), (75) and (76), we finally obtain that Equations (67) and (68) becomes

(77)

. (78)

Let

(79)

(80)

where we made the change of variables for solving the integrals.

We can write Equations (77) and (78) as follows

(81)

. (82)

On the other hand, by Equations (5) and (74) we have

Using Equation (70) we arrive to

(83)

. (84)

Finally, by Equations (81), (82), (83) and (84) we can turn Equation (65) into an algebraic equation as follows

This equation can be written as

(85)

In order to satisfy this equality for all, we will ask

. (86)

Then, Equation (85) becomes

This equation depends only on and and using Equations (79) and (80) it is easily proved that it is satisfied for all.

In order to satisfy, according to Equation (69) we have to ask

. (87)

By Equation (74), the other initial condition is satisfied by taking

(88)

where is given in Equation (11).

Finally, the trajectory equation is satisfied if and only if Equations (71), (86) and (87) hold, provided that and are real and that condition (72) is satisfied. This is a system of three equations where, and are the unknowns. Using Equations (66) and (80) it is proved that the solution is given by

(89)

(90)

(91)

where l is the angular momentum (which is known that is constant).

However, this solution holds only if. Using Equations (89) and (90) this condition is equivalent to

By this condition, we can obtain the minimum value of and then it is easily proved that the minimum value of E is given by

. (92)

If we can see in Equation (71) that is complex but according to Equation (91) is real which is a contradiction. Then the system of equations has not solution in the case and hence the solution given in Equation (69) does not work.

Next we will choose in order to satisfy condition (72). Provided that there are two cases, or (we will not consider the case).

In the first case, according to Equations (89) and (90), is positive and is real. In addition, using Equation (91) and the fact that with given in Equation (92) it is proved that is negative. In this case we will choose with. Then, according to Equation (70) we have

Using this result, and taking into account that is positive and is negative it is proved that condition (72) is satisfied.

In the second case, according to Equations (89), (90) and (91), is negative, is a pure imaginary complex number and is positive. In this case we will choose with i the imaginary unit and. Then, according to Equations (70) and (71) we have

Using these results it is proved that condition (72) is satisfied.

Finally, using that

the solution of the trajectory equation is given by

(93)

where, and are given in Equations (89), (90) and (91) and is given in Equation (92).

It is worthwhile to point out that we choose in the following way

. (94)

If, according to Equation (93), is the parametrization of an ellipse as was expected. The semi- major and semi-minor axis are given by and respectively and the center is given by. According to Equation (71), the focus of the ellipse is in the origin as Kepler’s first law says. We can obtain the semi-axes and the center in the traditional way and check that we arrive to Equations (89), (90) and (91). In addition, we can calculate the minimum value of the energy under the hypothesis we have a bound motion and check that we obtain Equation (92).

We can see in Equation (93) that and that

Hence, conditions (8) and (9) are satisfied and then the first step of the algorithm is complete.

We will just choose to complete the second step.

In order to find u, on the one hand, according to Equations (63) and (73) we have

By Equation (89) this expression turns out to be

. (95)

On the other hand, according to Equations (83) and (84) we obtain

According to Equation (71) we arrive to

. (96)

Finally, according to Equations (13), (95) and (96) we have

Using Equations (89) and (91) we can write this expression as follows

. (97)

We will choose in order to satisfy

Note that implies that is real and implies that is complex. Then this is consistent with the results obtained above. In addition, we will consider in both cases. Then we have

(98)

where is given by

. (99)

Finally, Equation (97) turns out to be

. (100)

On the other hand, using Equation (88) and the fact that is positive we arrive to

In addition, by Equations (94) and (98) it is easily proved that

which implies

. (101)

Finally, by Equations (100) and (101) and using condition (72) we obtain

However, according to Equation (89)

and then we just can write

Using Equations (70), (89) and (91) this equation can be written as follows

(102)

where is given by

(103)

and is given in Equation (92).

Note that since and then is positive.

Finally we complete the third step.

In this case we will not find the function y since it is not easy to find a function in order to solve the integral of Equation (17). However, in this case we can solve the temporal equation implicitly. According to Equations (2) and (102) and taking into account that this equation becomes

It is easily proved that the solution is given by

By Equation (98) we can write the solution depending the case as follows

(104)

where is given in Equation (99).

Finally, is the solution of Kepler’s problem (with the initial conditions given in Equation (64)) where is given in Equation (93) and is given by Equation (104).

Finally, we will obtain Kepler’s third law which says that the square of the orbital period is directly proportional to the cube of the semi-major axis.

In Equation (93) we can see that if, then is a periodic function whose period is given by. Then, according to Equation (104), the time it takes to “the planet”to make a full turn is given by

Using Equations (89) and (99) we finally arrive to

and then we proved Kepler’s third law.

5. Conclusion

We used the arc length function and its inverse in order to introduce a new way to graph functions by curving the axes as shown in Figure 10 and Figure 12. Using this, we found a more conveniently method to solve the temporal equation and then we changed the fourth step of the algorithm given in the first part in order to graph each component of the solution of Equation (1) as given in the mentioned figures. Following this algorithm, we solved the harmonic oscillator, the pendulum, the particle under the action of two elastic springs and Kepler’s problems. We were able to solve the pendulum and the particle under the action of two elastic springs problems without using elliptical integrals and to see the periods of both problems as the length of a curve given in Equations (43) and (58) respectively. Then, using this fact, we approximate the periods of both problems in Equations (46) and (61) with a relative error less than 0.17. Finally, in Kepler’s problem, we solved the trajectory equation and we proved that the solution describes an ellipse with focus in the origin (for some values of the energy). We could obtain the semi-major and semi-minor axes, the center of the ellipse and the orbital period by using this formalism.

Cite this paper

Federico Petrovich, (2016) A New Formulation of Classical Mechanics—Part 2. Journal of Applied Mathematics and Physics,04,939-966. doi: 10.4236/jamp.2016.45103

References