Journal of Applied Mathematics and Physics
Vol.04 No.06(2016), Article ID:67406,13 pages
10.4236/jamp.2016.46114
Mathematical Analysis of Nipah Virus Infections Using Optimal Control Theory
Jakia Sultana1, Chandra N. Podder2
1Department of Computer Science and Engineering, Green University of Bangladesh, Dhaka, Bangladesh
2Department of Mathematics, University of Dhaka, Dhaka, Bangladesh

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 March 2016; accepted 13 June 2016; published 16 June 2016
ABSTRACT
The optimal use of intervention strategies to mitigate the spread of Nipah Virus (NiV) using optimal control technique is studied in this paper. First of all we formulate a dynamic model of NiV infections with variable size population and two control strategies where creating awareness and treatment are considered as controls. We intend to find the optimal combination of these two control strategies that will minimize the cost of the two control measures and as a result the number of infectious individuals will decrease. We establish the existence for the optimal controls and Pontryagin’s maximum principle is used to characterize the optimal controls. The numerical simulation suggests that optimal control technique is much more effective to minimize the infected individuals and the corresponding cost of the two controls. It is also monitored that in the case of high contact rate, controls have to work for longer period of time to get the desired result. Numerical simulation reveals that the spread of Nipah virus can be controlled effectively if we apply control strategy at early stage.
Keywords:
Nipah Virus (NiV), Optimal Control, Existence of the State, Existence of the Objective Functional, Pontryagin’s Maximum Principle, Transversality Condition, Optimality Condition, Hamiltonian (H)

1. Introduction
Mathematical modeling has become an important tool for analyzing the spread as well as control of infectious diseases. It is also a useful tool for the measurement of the effect of different strategies for controlling the spread of infectious diseases within a population. In recent years epidemiological modeling of infectious disease transmission has had an increasing influence on the theory and practice of disease management and control [1] . There are a number of different methods for calculating the optimal control for a specific mathematical model. For example, Pontryagin’s maximum principle [2] allows the calculation of the optimal control for a system of ordinary differential equation with a given constraint. Here the optimal control strategy is used to minimize the infected individuals and to maximize the total number of recovered individuals.
Nipah virus, a member of the genus Henipavirus, a new class of virus in the Paramyxoviridae family, has drawn attention as an emerging zoonotic virus in south-east and south-Asian region [3] . This emerging infectious disease has become one of the most alarming threats of the public health mainly due to its periodic outbreaks and the high mortality rate [4] . Epidemiology is the study of the distribution and determinants of health related states or events in specified populations and the application of epidemiology is to control of health problems. The crucial point is that epidemiology concerns itself with populations or groups of population in contrast to clinical medicine, which deals with individuals (patients). Therefore, epidemiology describes health and disease in terms of frequencies and distributions of determinants and conditions in a population or in a specific group of a population. Although Nipah virus has caused only a few outbreaks, it infects a wide range of animals and causes severe disease and death in people, making it a public health concern [5] . Treatment is mostly symptomatic and supportive as the effect of antiviral drugs is not satisfactory. So the very high case fatality addresses the need for adequate and strict control and preventive measures.
This paper deals with application of optimal control to a dynamic model of Nipah Virus (NiV) infections and its possible control and preventive strategy with the help of optimal control technique. Our aim is to minimize the total number of infectious individuals and the cost which is related for creating awareness and treatment.
2. Formulation of Model
Nipah virus infection is a zoonotic virus and transmitted first from animal to human. Once it has been transmitted to human, then it continues to be transmitted through human to human (H2H) by the close contact of infected individuals due to its highly infectivity [6] . Let us suppose that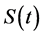 ,
,  and
and  denote the number of individuals in the susceptible, infectious and recovered classes at time t respectively. The total population at time t is represented by
denote the number of individuals in the susceptible, infectious and recovered classes at time t respectively. The total population at time t is represented by .
.
We consider the following system of non-linear differential equation, is a type of standard SIR disease model, to describe the dynamics of Nipah Virus (NiV) infections in the community.
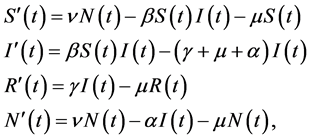 (1)
(1)
with initial conditions,
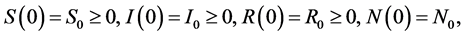 (2)
(2)
and where, the parameter 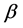 represents the effective contact rate,
represents the effective contact rate, 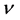 is the natural birth rate,
is the natural birth rate,  is the natural mortality rate,
is the natural mortality rate, 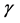 is the recovery rate and
is the recovery rate and  represents the disease induced death rate.
represents the disease induced death rate.
Since there is no proper vaccination program or appropriate drugs for NiV infections, so in the model we introduce two control strategies, namely, creating awareness (u1) among the community about the risky areas before outbreak of the disease and the treatment (u2). Here the control 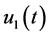 measures the effort to be needed to increase awareness which results in the reduction of the transmission rate (
measures the effort to be needed to increase awareness which results in the reduction of the transmission rate (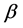 ) and the control
) and the control  measures the effort required for giving health cares for the infected people to reduce the infected individuals.
measures the effort required for giving health cares for the infected people to reduce the infected individuals.
Now the NiV model with two control strategies is given below:
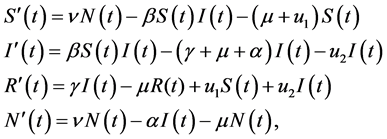 (3)
(3)
with initial conditions,

Here our main objective is to minimize the total number of infected individuals and to reduce the cost which is needed for creating awareness and treatment on a specified time interval. For the fulfillment of our purpose, we work with the following objective function which is similar as [7] .
where, B1 and B2 are weight parameters that help to balance the corresponding costs. We define the control set as follows:
In the objective function, A1I represents the total number of infected individuals, 

3. Existence of the Optimal Control for NiV Model
3.1. Existence of the State
Adding first three equations of the system (3) we get,
On integrating we get,
So we have
From the fourth equation of (3) we have
and then
So, finally we get
Since



3.2. Existence of the Objective Functional
By proving the following theorem we can establish the existence of the objective functional:
Theorem 1. Consider the control problem with system (3). Then there exists optimal controls 


Proof: To use an existence result in [8] , we must check the following properties [9] .
1) The set of controls and corresponding state variables is non-empty.
2) The control set U is convex and closed.
3) The right-hand side of the state system is bounded by a linear function in the state and control variables.
4) The integrand of the objective functional is convex on U and is bounded below by 



To prove the above theorem we need to use the following theorem 2 and 3.
Theorem 2. Let each of the functions 
be continuous in a region 






that also satisfies the initial conditions
Theorem 3. Let 







Now with the help of the above two theorems we prove the four conditions of theorem (1).
Proof of theorem 1: To use an existence result in [8] , we must check the following properties [9] .
1) The set of controls and corresponding state variables is non-empty.
2) The control set U is convex and closed.
3) The right-hand side of the state system is bounded by a linear function in the state and control variables.
4) The integrand of the objective functional is convex on U and is bounded below by 



Proof of 1): Let us consider,
where, F1, F2, F3 and F4 buildup the right hand side of the system (3). Let 

So by following the theorem 3, we can say that there exists an unique solution



Proof of 2): By definition, U is closed. Take any controls 

Additionally, observe that 

Hence, 


Proof of 3):
We consider,
The state system is given below:
Now we rewrite the system in matrix form:

where,

and

which gives a linear function of the controls u1 and u2 defined by time and state variables. Then we can find out the bound of the right hand side. It is noted that all parameters are constant and greater than or equal to zero. Therefore we can write,
where

Proof of 4):
For the proof of the condition 4) we use the result in [10] and [Fleming and Rishel (1975)]. The control and the state variables are non-negative values and are non-empty. In the minimization problem, the necessary convexity of the objective functional in u1 is satisfied. The control variables 

Now we have to prove that 



Here,
where, 



4. Characterization of the Optimal Control
In order to derive the necessary condition for the optimal control, we use pontryagin’s maximum principle [2] . This principle converts the system and the objective functional into a problem minimizing pointwise a Hamiltonian H with respect to u1 and u2. In the objective function, the value A is the balancing parameter, B1 and B2 are the weight parameters balancing the cost. Here we can see from the system (3) that R appears only in the recovered class. So, when we build up the optimality system, we will ignore the recovered class.
By using pantraygin’s Maximum principle we first derive the Hamiltonian which is given below

where, λS, λI, λN are the associated adjoints for the state S, I, N respectively. By differentiating the Hamiltonian (H) with respect to each state variable, we find the differential equation for the associated adjoint. Hence, the adjoint system is,

with the final conditions,
So by differentiating the Hamiltonian with respect to two controls u1 and u2 we obtain:
and
5. Optimality System
State equations:

with initial conditions,

Adjoint equations:

Transversality equations:

Characterization of the optimal control 


and

In compact notion we can write,

and

6. Numerical Results and Discussions
Numerical solutions to the optimal system are executed using MATLAB. The considered two controls (u1, u2) depend on the adjoints λS, λI and λN of the state variables S, I and N respectively. We simulate the model without control and with control and then we compare the results. We considered the numerical value of the controls u1 and u2 in between zero(0) and one(1) as they are not 100 percent effective. We also monitored the effectiveness of the weight parameter to see how the control is related to weight function. In this simulation we assumed the initial values of S, I and N as proportions instead of whole numbers.
The parameter values used in the simulations are presented in the following Table 1.
Figure 1 depicts the importance of the controls to the disease dynamics. From the graphs, we see that the control has a positive impact to reduce infection until the controls are effective enough. It is also clear from the figures that the disease can be controlled over finite period of time after imposing control strategies.
Figure 2 and Figure 3 monitored the impact of the parameter (a) of disease induced death rate. Here we see if a is at a low rate (a = 0.3) then the controls work effectively and as a result there is a significant reduction of the infections. When controls do not work it resulted the increase of infected individuals.
On the other hand for the higher rate of a (where awareness does not work, u1 = 0 and the treatment u2 works for a short period of time) there is a sharp decrease of infection due to death resulting the existence of fewer recovered people.
Figure 4 and Figure 5 show the comparative situation of the disease dynamics for low and high contact rates. In the case of low contact rate (b = 0.2), the infectious individuals decrease until the controls work effectively and as a result there is a notable increment of recovered individual.
On the other hand, for the very high contact rate (b = 2), which resulted a severe disease burden, the controls work for a longer period of time to reduce the disease burden.
Figure 6 and Figure 7 show the influence of the various weight parameters. Here we notice that for low
Table 1. Description and parameter values of the NiV model.
Figure 1. NIV model with control and without control, parameter values are taken from Table 1.
Figure 2. NiV model with low disease induced death rate, α = 0.3 and other parameter values are taken from Table 1.
Figure 3. NiV model with high disease induced death rate, α = 3 and other parameter values are taken from Table 1.
Figure 4. NiV model with low contact rate, β = 0.2 and other parameter values are taken from Table 1.
Figure 5. NiV model with high contact rate, β = 2 and other parameter values are taken from Table 1.
Figure 6. NiV model with low weight parameters, B1 = 0.2, B2 = 0.3 and other parameter values are taken from Table 1.
Figure 7. NiV model with high weight parameters, B1 = 2, B2 = 3 and other parameter values are taken from Table 1.
weight parameters (B1 = 0.2, B2 = 0.3) the infectious individuals decrease sharply for first few years (as the controls work at maximum level). It is also noticed that the infected individuals start to increase when the effectiveness of the controls start to decrease.
In the case of high weight parameter values (B1 = 2, B2 = 3) the high effectiveness of the controls are monitored and as a result there is a sharp reduction of infection during that effective level.
7. Conclusions
The important findings are given below:
・ A comparison between with and without control strategy is monitored. The effect of control parameters is very much notable for reducing the infected individuals to control the disease dynamics.
・ The controls need to be effective for longer period of time in case of high incidence.
・ The optimal control is much more effective to minimize the infected individuals (as a result recovered individuals will be maximized) and also to minimize the cost of the two control measures.
・ For low weight parameter values, the controls show their effectiveness at a maximum level.
・ From the simulations it is monitored that the optimal combination of treatment and creating awareness is very prominent for disease elimination.
Acknowledgements
The author, JS acknowledge, with thanks, the support in part of the National Science and Technology (NST), Dhaka. The authors are grateful to the reviewers for their constructive comments.
Cite this paper
Jakia Sultana,Chandra N. Podder, (2016) Mathematical Analysis of Nipah Virus Infections Using Optimal Control Theory. Journal of Applied Mathematics and Physics,04,1099-1111. doi: 10.4236/jamp.2016.46114
References
- 1. Chong, H.T., Hossain, M.J. and Tan, C.T. (2008) Differences in Epidemiologic and Clinical Features of Nipah Virus Encephalitis between the Malaysian and Bangladesh Outbreaks. Neurology Asia, 13, 23-26.
- 2. Pontryagin, L.S., Boltyanskii, V.G., Gamkrelize, R.V. and Mishchenko, E.F. (1962) The Mathematical Theory of Optimal Processes. New York, Wiley.
- 3. (2008) Nipah Virus Infections. WHO Report, Asia-Pacific Region, World Health Organization.
- 4. (2011) National Guideline for Management, Prevention and Control of Nipah Virus Infection including Encephalitis, Directorate General of Health Services. Ministry of Health and Family Welfare, Government of the People’s Republic of Bangladesh.
- 5. (2004) Nipah Virus: Vaccination and Passive Protection Studies in a Hamster Model. Journal of Virology, 78, 834-840.
http://dx.doi.org/10.1128/JVI.78.2.834-840.2004 - 6. Biswas, M.H.A. (2014) Optimal Control of Nipah Virus (NIV) Infections: A Bangladesh Scenario. Journal of Pure and Applied Mathematics: Advances and Applications, 12, 77-104.
- 7. Bakare, E.A., Nwagwo, A. and Danso-Addo, E. (2014) Optimal Control Analysis of an SIR Epidemic Model with Constant Recruitment. International Journal of Applied Mathematical Research, 3, 273-285.
http://dx.doi.org/10.14419/ijamr.v3i3.2872 - 8. Fleming, W.H. and Rishel, R.W. (1975) Deterministic and Stochastic Optimal Control. Springer Verlag, New York.
http://dx.doi.org/10.1007/978-1-4612-6380-7 - 9. Yusuf, T.T. and Benyah, F. (2012) Optimal Control of Vaccination and Treatment for an SIR Epidemiological Model. World Journal of Modelling and Simulation, 8, 194-204.
- 10. Hsieh, Y. and Sheu, S. (2001) The Effect of Density-Dependent Treatment and Behaviour Change on the Dynamics of HIV Transmission. Journal of Mathematical Biology, 43, 69-80.
http://dx.doi.org/10.1007/s002850100087






































































