Journal of Applied Mathematics and Physics
Vol.04 No.04(2016), Article ID:66103,13 pages
10.4236/jamp.2016.44087
Flow through a Variable Permeability Brinkman Porous Core
M. S. Abu Zaytoon, T. L. Alderson, M. H. Hamdan*
Department of Mathematical Sciences, University of New Brunswick, Saint John, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 February 2016; accepted 24 April 2016; published 28 April 2016
ABSTRACT
In this work, we consider the flow through composite porous layers of variable permeability, with the middle layer representing a porous core bounded by two Darcy layers. Brinkman’s equation is valid in the middle layer and has been reduced to an Airy’s inhomogeneous differential equation. Solution is obtained in terms of Airy’s functions and the Nield-Kuznetsov function.
Keywords:
Airy’s Functions, Variable Permeability Porous Layers

1. Introduction
Fluid flow through and over porous layers has been receiving increasing interest in the porous media literature for over half a century, due to the importance of this type of flow in industrial and natural situations including lubrication problems, heating and cooling system design, groundwater flow, and the movement of oil and gas in earth layers [1] - [4] . Much of the work in this field has been devoted to the derivation of appropriate conditions at the interface between a fluid and a porous layer, or at the interface between two composite porous layers [5] - [9] . Various flow models have also been tested to find the most appropriate model to use in a given flow situation, and the most appropriate model that provides compatibility with the Navier-Stokes equations [2] [10] [11] .
Many excellent reviews are available in the literature which has been centred on the problem of flow through and over porous layers of constant permeability [1] [10] - [13] . More recently, however, there has been increasing interest in the use of Brinkman’s equation with variable permeability due to the usefulness of Brinkman’s equation in modelling the flow in the transition layer between a Darcy porous medium and Navier-Stokes channel. In fact, this has been extensively analyzed by Nield and Kuznetsov [14] in their introduction of the variable permeability transition layer. Their analysis introduced the use of Brinkman’s equation to model the flow in which they chose a permeability function that reduced Brinkman’s equation into an Airy’s differential equation.
It is worth noting that there exist a large number of functions that can be used to model the variable permeability and result either in an Airy’s equation or in a different special differential equation. In the current work we will introduce a permeability function that is suitable for describing permeability variations in a Brinkman layer bounded two Darcy layers of variable permeability. This will be used in the analysis of the problem of flow through a variable permeability Brinkman porous channel bounded on either side by a variable permeability Darcy layer. The Darcy layers are terminated on their outer sides by solid, impermeable walls. This problem is representative of flow in a porous channel with a porous core that is of different porosity and permeability than its bounding porous lining.
A main objective of this undertaking is to study the effects of thin porous Darcy layers on the variable permeability flow in a Brinkman layer. In order to accomplish this work, we choose a Brinkman permeability function that reduces Brinkman’s equation to the well-known inhomogeneous Airy’s differential equation [15] . We provide an analytical solution to the resulting Airy’s inhomogeneous equation, and we provide computations using Maple’s built-in functions to evaluate Airy’s functions.
2. Problem Formulation
Consider the flow configuration in Figure 1. The flow domain is a channel composed of three porous layers, where the flow in the middle layer is governed by Brinkman’s equation with variable permeability, and in the lower and upper layers with variable permeability Darcy law. The channel is bounded by solid, impermeable walls at  and
and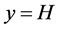 .
.
In setting up the above flow problem, we make the following assumptions that are essential for the current work.
1) In the lower Darcy regiment, permeability is an increasing function of y. It starts at zero on the lower macroscopic wall and reaches a maximum, 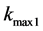 , at the lower interface (y = D) of the Brinkman layer.
, at the lower interface (y = D) of the Brinkman layer.
2) In the upper Darcy regiment, permeability is a decreasing function of y. It starts at its maximum, 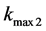 , at y = L (the upper interface with the Brinkman layer) and drops to zero on the upper macroscopic wall (y = H).
, at y = L (the upper interface with the Brinkman layer) and drops to zero on the upper macroscopic wall (y = H).
3)  due to the choice of decreasing permeability distribution in the Brinkman regime.
due to the choice of decreasing permeability distribution in the Brinkman regime.
4) All permeability functions are assumed continuous. At each interface, the permeability of the lower channel is equal to permeability of the upper channel. However, the rates of change of Darcy permeability are not necessarily equal at the interfaces.
5) At each interface, we assume velocity continuity and shear stress continuity.
6) Flow is driven by the same constant pressure gradient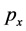 .
.
7) Solutions below will depend on  and
and 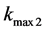 whose values will be determined from given permeability distributions in the Darcy regiments.
whose values will be determined from given permeability distributions in the Darcy regiments.
8) We will choose  so that the Brinkman permeability remains finite (for the function chosen in this work).
so that the Brinkman permeability remains finite (for the function chosen in this work).
Figure 1. Representative sketch.
Equations governing the flow in the three regions in Figure 1 are as follows.
For :
: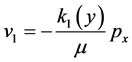 (1)
(1)
For :
: (2)
(2)
For :
:
where in 




Boundary conditions associated with the above flow are as follows.
2.1. Conditions on Upper and Lower Walls

2.2. Conditions at the Interfaces y = D and y = L

3. Solution Methodology
Darcy’s Equations (1) and (3) are algebraic equations from which we can determine the velocities once the pressure gradient and viscosity are given, and the permeability distributions (i.e.









Once 






Solution to Brinkman’s equation is given in terms of Airy’s functions. These are computed in this work using Maple’s built-in functions.
3.1. Solution to Brinkman’s Equation in the Middle Layer
In this work we consider the variable permeability distribution in the Brinkman layer to be given by the following expression that satisfies 


Using (6) in (2) reduces Equation (2) to the form

where


Now, letting

and

then

and

Equation (7) then becomes:

Equation (14) is Airy’s inhomogeneous equation, which admits the following general solution for 

where 



Equation (15) takes the following form in terms of the original variable y:

and the following form in terms of the original velocity

It is convenient at this stage to introduce the following dimensionless variables with respect to a characteristic length M, in which the quantities identified by an asterisk (*) are dimensionless:

Dropping the asterisk (*), we obtain the following dimensionless equations:
Permeability distribution in Brinkman’s layer:

Velocity distribution in Brinkman’s layer:

Shear stress distribution in Brinkman’s layer:

where prime notation denotes differentiation with respect to the respective arguments.
Velocity at the interfaces between layers:


where in:







3.2. Darcy Expressions in the Bounding Layers
Solution to Brinkman’s equation, obtained above is predicated upon 



4. Results and Analysis
The dimensionless forms of linear, quadratic and exponential permeability distributions and associated velocity distributions for the Darcy layers, together with the shear stress terms, summarized in Table 1, above, are used to generate Table 2, which lists the values of permeability, velocity and shear stress term at the lower and upper interfaces between layers in terms of the permeability at the lower interface



Dependence of permeability profiles on the thickness of the porous layers is illustrated in Table 3 by taking D = 0.1, L = 0.9 and H = 1 for a thick middle layer, and in Table 4 with D = 0.4, L = 0.6 and H = 1 for a thin middle layer. Permeability distributions in the lower and upper bounding Darcy layers are given in Table 3 and Table 4, as functions of y, and permeability distribution in the middle, Brinkman layer is calculated by the dimensionless expression of equation (20) and given in Table 3 and Table 4 for chosen values of 

Tables 5-10 document the values of velocities and shear stresses at the interfaces between the porous layers, and list values of parameters involved in velocity computations. It should be emphasized here that some of the computed values of velocity and shear stresses become inaccurate or extremely large for small values Da, hence not listed in this work. This may be attributed to inaccuracy in computations and approximations of Airy’s functions when Da is small (that is, when Da < 0.001).
Graphs illustrating linear, quadratic, and exponential permeability profiles are illustrated in Figures 2(a)-(c). These figures show the relatives shapes of the permeability distribution in each of the layers, and the decreasing permeability in the middle layer. How the permeability distributions affects the velocity profiles across the layers is illustrated in Figures 3(a)-(e). These figures show regions of expected increase and decrease in the velocity across the layers in a manner that is reflective of the increase and decrease in the permeability profiles.
5. Conclusion
In this work we considered flow through composite porous layers of variable permeability. The problem considered is that of a porous core the flow through is governed by Brinkman’s equation for variable permeability media, while the core is bounded by two Darcy layers of variable permeability. Various types of variable Darcy
Table 1. Dimensionless permeability, velocity, and shear stress terms for darcy layers.



Figure 2. (a) Permeability distribution for linear permeability functions, kmax1 = 1, D = 1/3, L = 2/3, and different values of kmax2. (b) Permeability distribution for quadratic permeability functions, kmax1 = 1, D = 1/3, L = 2/3, and different values of kmax2. (c) Permeability distribution for exponential permeability functions, kmax1 = 1, D = 1/3, L = 2/3, and different values of kmax2.
Table 2. Dimensionless permeability, velocity, and shear stress terms at the lower and upper interfaces.
Table 3. Dependence of permeability profiles on the thickness of the porous layers: thick layer.
Table 4. Dependence of permeability profiles on the thickness of the porous layers: thin layer.
Table 5. Values of dimensionless α, β, U1, and U2 for D = 1/3, L = 2/3 and different values of 

Table 6. Values of dimensionless



Table 7. Values of dimensionless 



Table 8. Value of 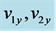







Figure 3. (a) Velocity profiles for linear permeability function, θ = 1, D = 1/3, L = 2/3, kmax = 1, and different values of kmax2. (b) Velocity profiles for linear permeability function, θ = 1, kmax = 0.1, D = 1/3, L = 2/3, and different values of kmax2. (c) Velocity profiles for quadratic permeability functions, θ = 1, kmax = 1, D = 0.1, L = 0.9, and different values of kmax2. (d) Velocity profiles for quadratic permeability functions, θ = 1, kmax = 0.1, D = 0.25, L = 0.75, and different values of kmax2. (e) Velocity profiles for exponential permeability functions, θ = 1, kmax = 1, D = 0.25, L = 0.75, and different values of kmax2.
Table 9. Value of 


Table 10. Values of 


permeability have been considered and solution to flow through the Brinkman layer is cast in terms of Airy’s and the Nield-Koznetsov functions.
Cite this paper
M. S. Abu Zaytoon,T. L. Alderson,M. H. Hamdan, (2016) Flow through a Variable Permeability Brinkman Porous Core. Journal of Applied Mathematics and Physics,04,766-778. doi: 10.4236/jamp.2016.44087
References
- 1. Alazmi, B. and Vafai, K. (2001) Analysis of Fluid Flow and Heat Transfer Interfacial Conditions between a Porous Medium and a Fluid Layer. International Journal of Heat and Mass Transfer, 44, 1735-1749.
http://dx.doi.org/10.1016/S0017-9310(00)00217-9 - 2. Alazmi, B. and Vafai, K. (2000) Analysis of Variants within the Porous Media Transport Models. Journal of Heat Transfer, 122, 303-326.
- 3. AbuZaytoon, M.S. (2015) Flow through and over Porous Layers of Variable Thicknesses and Variable Permeability. PhD Thesis, University of New Brunswick, Saint John, Canada.
- 4. Vafai, K. and Thiyagaraja, R. (1987) Analysis of Flow and Heat Transfer at the Interface Region of a Porous Medium. International Journal of Heat and Mass Transfer, 30, 1391-1405.
http://dx.doi.org/10.1016/0017-9310(87)90171-2 - 5. Vafai, K. and Tien, C.L. (1981) Boundary and Inertia Effects on Flow and Heat Transfer in Porous Media. International Journal of Heat and Mass Transfer, 24, 195-203.
http://dx.doi.org/10.1016/0017-9310(81)90027-2 - 6. Beavers, G.S. and Joseph, D.D. (1967) Boundary Conditions at a Naturally Permeable Wall. Journal of Fluid Mechanics, 30, 197-207.
http://dx.doi.org/10.1017/S0022112067001375 - 7. Ochoa-Tapia, J.A. and Whitaker, S. (1995) Momentum Transfer at the Boundary between a Porous Medium and a Homogeneous Fluid: I) Theoretical Development. International Journal of Heat and Mass Transfer, 3, 2635-2646.
http://dx.doi.org/10.1016/0017-9310(94)00346-W - 8. Ochoa-Tapia, J.A. and Whitaker, S. (1995) Momentum Transfer at the Boundary between a Porous Medium and a Homogeneous Fluid: II) Comparison with Experiment. International Journal of Heat and Mass Transfer, 3, 2647-2655.
http://dx.doi.org/10.1016/0017-9310(94)00347-X - 9. Vafai, K. and Kim, S.J. (1990) Fluid Mechanics of the Interface Region between a Porous Medium and a Fluid Layer: An Exact Solution. International Journal of Heat and Fluid Flow, 11, 254-256.
http://dx.doi.org/10.1016/0142-727X(90)90045-D - 10. Parvazinia, M., Nassehi, V., Wakeman, R.J. and Ghoreishy, M.H.R. (2006) Finite Element Modelling of Flow through a Porous Medium between Two Parallel Plates Using the Brinkman Equation. Transport in Porous Media, 63, 71-90.
http://dx.doi.org/10.1007/s11242-005-2721-2 - 11. Joseph, D.D., Nield, D.A. and Papanicolaou, G. (1982) Non-linear Equation Governing Flow in a Saturated Porous Medium. Water Resources Research, 18, 1049-1052.
http://dx.doi.org/10.1029/WR018i004p01049 - 12. Chandesris, M. and Jamet, D. (2006) Boundary Conditions at a Planar Fluid-Porous Interface for a Poisueille Flow. International Journal of Heat and Mass Transfer, 49, 2137-2150.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2005.12.010 - 13. Sahraoui, M. and Kaviany, M. (1992) Slip and No-slip Velocity Boundary Conditions at Interface of Porous, Plain Media. International Journal of Heat and Mass Transfer, 35, 927-943.
http://dx.doi.org/10.1016/0017-9310(92)90258-T - 14. Nield, D.A. and Kuznetsov, A.V. (2009) The Effect of a Transition Layer between a Fluid and a Porous Medium: Shear Flow in a Channel. Transport in Porous Media, 87, 477-487.
http://dx.doi.org/10.1007/s11242-009-9342-0 - 15. Hamdan, M.H. and Kamel, M.T. (2011) On the Ni(x) Integral Function and Its Application to the Airy’s Non-Homogeneous Equation. Applied Mathematics and Computation, 217, 7349-7360.
http://dx.doi.org/10.1016/j.amc.2011.02.025
NOTES
*Corresponding author.




