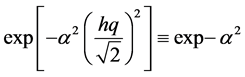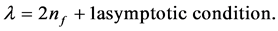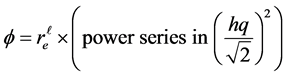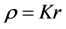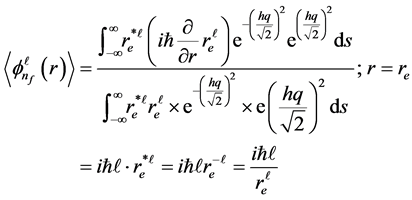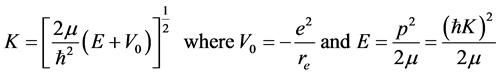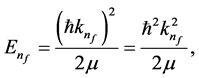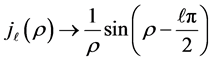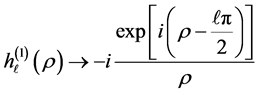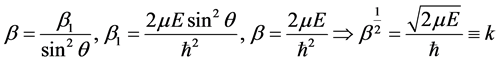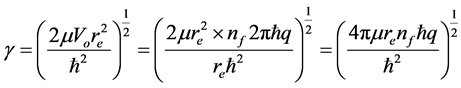Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63802,8 pages
10.4236/jamp.2016.42039
Eigenfunctions for a Quantum Wire on a Single Electron at Its Surface and in the Quantum Well with Beaded Fractional Quantized States for the Fractional Charges
Saleem Iqbal1, Farhana Sarwar1,2, Syed Mohsin Raza3
1Department of Mathematics, University of Balochistan, Quetta, Pakistan
2Department of Mathematics, F. G. Girls Degree College, Quetta, Pakistan
3Department of Physics, University of Balochistan, Quetta, Pakistan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 January 2016; accepted 22 February 2016; published 25 February 2016
ABSTRACT
We developed energy profiles for the fractional quantized states both on the surface of electron due to overwhelming centrifugal potentials and inside the electron at different locations of the quantum well due to overwhelming attractive electrodynamic potentials. The charge as a physical constant and single entity is taken as density and segments on their respective sub-quanta (floats on sub quanta) and hence the fractional charge quantiz at in. There is an integrated oscillatory effect which ties all fractional quantized states both on the surface and in the interior of the volume of an electron. The eigenfunctions, i.e., the energy profiles for the electron show the shape of a string or a quantum wire in which fractional quantized states are beaded. We followed an entirely different approach and indeed thesis to reproducing the eigenfunctions for the fractional quantized states for a single electron. We produced very fascinating mathematical formulas for all such cases by using Hermite and Laguerre polynomials, spherical based and Neumann functions and indeed asymptotic behavior of Bessel and Neumann functions. Our quantization theory is dealt in the momentum space.
Keywords:
Fractional Charge Quantization, Fractional Fourier Transform, Hermite Polynomials, Sub Quanta of Electron, Spherical Bessel and Neumann Functions, Lagueree Polynomials

1. Introduction
The inside of the electron is treated like a potential well with its depth equivalent to radius 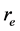 and that the charge above it is fractionally quantized. The bounded electron having orbit angular and rotational momentum will have a continuous change of its surface, as a consequence of which, charges as a constant entity will rearrange in its fragmented form and hence the fractional quantized states above its surface. Each fractional quantized state is a manifestation of sub quanta due to change in mass distribution. This happens in the momentum space just like the Compton and Photoelectric effects. We are refereing to momentum space because some kind of external momentum, may be due to photons, will cause the charge on an electron to become degenerate, of course, only above the surface. The fractional charge floats on the surface of sub quanta (energy becomes oscillatory due to segmented masses of electron but coupled with a string or a quanta wire). The question why and how this happens could be answered by considering that the centrifugal potential is dominating over the electrodynamic potential, as a consequence of which,quantum well with a depth
and that the charge above it is fractionally quantized. The bounded electron having orbit angular and rotational momentum will have a continuous change of its surface, as a consequence of which, charges as a constant entity will rearrange in its fragmented form and hence the fractional quantized states above its surface. Each fractional quantized state is a manifestation of sub quanta due to change in mass distribution. This happens in the momentum space just like the Compton and Photoelectric effects. We are refereing to momentum space because some kind of external momentum, may be due to photons, will cause the charge on an electron to become degenerate, of course, only above the surface. The fractional charge floats on the surface of sub quanta (energy becomes oscillatory due to segmented masses of electron but coupled with a string or a quanta wire). The question why and how this happens could be answered by considering that the centrifugal potential is dominating over the electrodynamic potential, as a consequence of which,quantum well with a depth 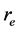 is becoming shallow and that the segmented masses of electron are shifting on the surface but coupled with a
is becoming shallow and that the segmented masses of electron are shifting on the surface but coupled with a
string. This coupling, in fact, is due to gyroscopic behaviour of an electron. The coupling constant 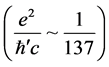 is overwhelmed by the gyroscopic constant,
is overwhelmed by the gyroscopic constant,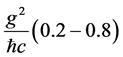 . The gyroscopic behaviour of an electron causes the
. The gyroscopic behaviour of an electron causes the
constant entity of charge to become degenerate and fractionally quantized above its surface (of course due to segmented mass distribution but coupled with a string at different locations just above the surface).
The radial eigen function 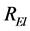 inside the quantum well (with depth equivalent to radius of an electron) follows strips of whirling pool as a manifestation of competing centrifugal force and attractive electrodynamic potentials. The charges always reside either on the surface of the electron or on the surface of a quanta.With this competing behaviour the shape of the surface of an electron is changed preferably due to the shallowing of quantum well. The brim of quantum well becomes effective due to overwhelming behaviour of the centrifugal potential over the attractive electrodynamic potential and hence the spitting of the segmented masses (sub quanta) above the surface. But all the erupted segmented masses are coupled with a central force and indeed with a string. Each segmented mass of an electron is equivalent to its sub quanta. These sub quanta of electrons are tied with each other with a gyroscopic behaviour. The charge is also fragmented and floats on their respective sub quanta.
inside the quantum well (with depth equivalent to radius of an electron) follows strips of whirling pool as a manifestation of competing centrifugal force and attractive electrodynamic potentials. The charges always reside either on the surface of the electron or on the surface of a quanta.With this competing behaviour the shape of the surface of an electron is changed preferably due to the shallowing of quantum well. The brim of quantum well becomes effective due to overwhelming behaviour of the centrifugal potential over the attractive electrodynamic potential and hence the spitting of the segmented masses (sub quanta) above the surface. But all the erupted segmented masses are coupled with a central force and indeed with a string. Each segmented mass of an electron is equivalent to its sub quanta. These sub quanta of electrons are tied with each other with a gyroscopic behaviour. The charge is also fragmented and floats on their respective sub quanta.
2. Theory
For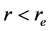 , i.e..,less than the radius or depth of the quantum well of an electron, the radial eigen function follows the equation [1] - [3] .
, i.e..,less than the radius or depth of the quantum well of an electron, the radial eigen function follows the equation [1] - [3] .
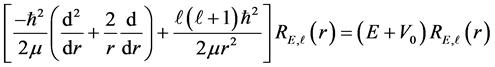
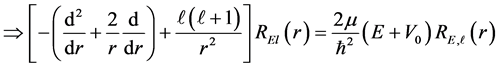 (1)
(1)
where 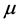 is the reduced or segmented masses,
is the reduced or segmented masses, 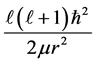 the centrifugal potential on each strip of the whirling pool inside the electron (quantum well),
the centrifugal potential on each strip of the whirling pool inside the electron (quantum well),  the electrodynamic potential and l the azimuthal
the electrodynamic potential and l the azimuthal
quantum number (determines the shape of the whirling strips in the quantum well). We roughly estimated the radius or depth of the quantum well of an electron by considering the charge as density of electron
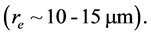 Our assumption for treating the charge as density is due to very small volume of the electron.
Our assumption for treating the charge as density is due to very small volume of the electron.
Each of the broken sub quanta are woven in a string due to whirling and swirling effects (electro weak interactions) on an electron and is manifestation of gyroscopic behaviour. Equation (1) can be rewritten as
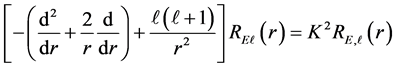 (2)
(2)
where
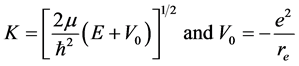 (3)
(3)
When broken sub quanta above the surface of an electron are woven in a string, they should have an integrated oscillatory effects.
Writing
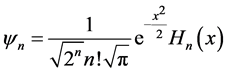 (4)
(4)
The exponent n of 2 will have fractional quantization, 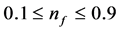
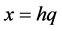
where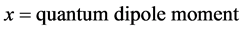
The matter energy such as of an electron exists in the form of transverse wave.This is oscillatory (quantum action) and configures a space called a wave packet or “quanta”. We consider that the charge on an electron is treated as its density which is not only smeared on the surface but also inside the volume despite the fact that charges always reside on the surface. This is the reason that fractional charges float on their respective segmented masses above the surface of an electron. Considering the symmetry of the harmonic oscillator potential,solution for eigen function exists in the form
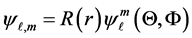
in which the differential equation for the radial eigen function (on the surface of an electron) 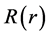
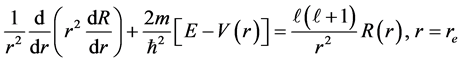
Modifying Equation (4) with Equation (5) for fractional charge quantized states having an integrated oscillatory effect at the surface of an electron.
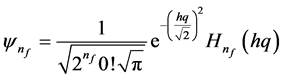
We have calculated 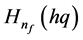
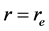
2.1. Case I (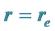
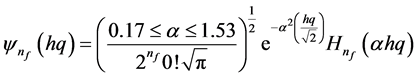
where 
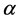
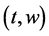
found 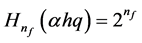
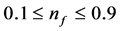
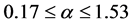
tends to unity and is valid for Equation (8). The reason for the convergence in the above expression is explained in [8] . The eigenfunction 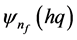
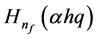
shows the energy profile as a straight line with fractional quantum states and that the profile is a tangent on the surface of an electron. The fractional quantum states 
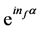
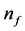
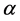
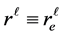
Writing the series for Equation (10), i.e..,
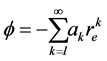
Using this series Equation (11) and making it to terminate with asymptotic condition, we have the recurrence relation (to reproduce the more appropriate shape of the string on the surface of an electron).
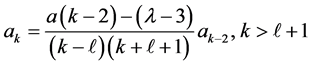
and Ultimately,we get the series in the form
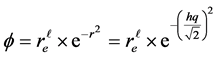
When centrifugal potential dominates over the attractive electrodynamic potential in the quantum well with its depth equal to radius of an electron swirling causes the strips of the whirlpool to change into elliptic orbits with enhanced Eulerian angles. Thus we have
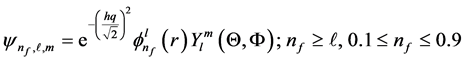
With Equation (14), 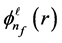
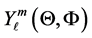
and
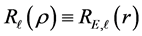
With Equation (15) and 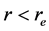
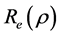
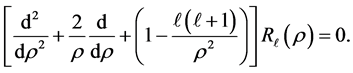
The particular solutions of Equation (16) are spherical Bessel functions
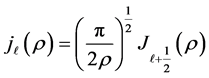
and the spherical Neumann functions
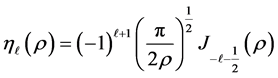
Just as in the case of the free particle the condition that 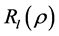
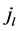
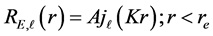
where A is complex constant and can be determined by normalizing the eigen functions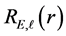
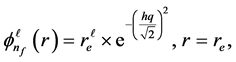
by using momentum operator for fractional charge quantization
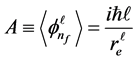
Putting Equation (20) in Equation (19), we have
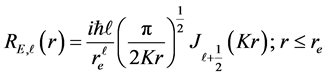
Equation (21) represents the eigenfunction of the swirling strips of the whirl pool in the quantum well. Using Equation (15) in Equation (17) and modifying Equation (21), we have
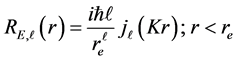
For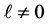
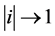
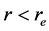
2.2. Case II (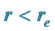
The value of K expressed in Equation (3) will further be modified for Equation (23)
For fractional charge quantization,
we have
We consider 
Thus the logarithmic derivative 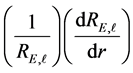
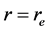
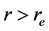
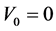
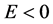
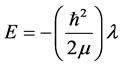
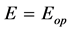
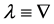
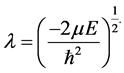
Equation (1) with 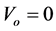
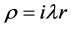
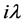
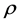
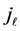
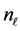
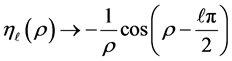
The asymptotic behaviour of the spherical Hankel functions of first and second kind with 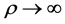
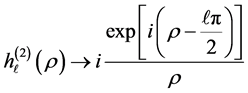
With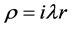
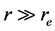
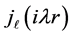
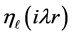
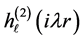
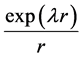
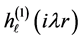
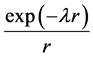
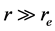
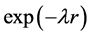
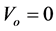
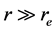
2.3. Case III (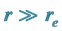
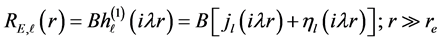
where B is a complex constant and can be determined by normalizing the eigenfunction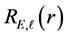
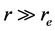
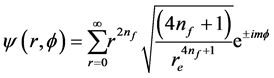
with theoretical eigenvalues
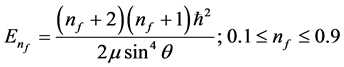
The complex constant B in Equation (28) at 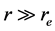
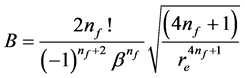
with
(for a free particle).
Remember
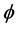
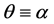
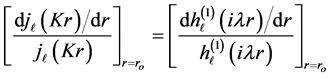
Equation (32) is the transcendental equation for arbitrary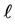
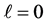
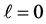
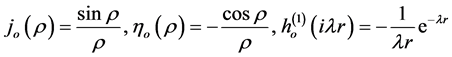
and
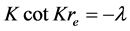
Equation (34) refers to odd parity solution to quantum potential well. Thus, setting 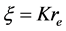
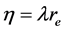
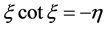
with
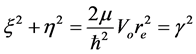
where 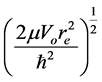
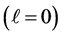
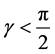
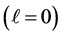
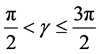
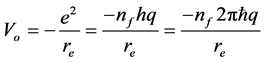
(by ignoring the negative sign because it shows attractive electrodynamic potential) in
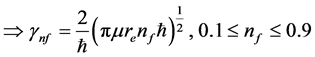
Equation (38) shows the strength of the quantum well at different depths for whirling strips corresponding to fractional quantized states inside the electron.
3. Conclusion
The energy profile (eigenfunctions) of the quasi particle nature of electron quanta is obtained. These energy profiles of stretched electron quanta with sub-quanta (twiggs) on the lateral surface in the momentum space due to twisting (gyroscopic behaviour) will pave a new dimension in theoretical physics to let us know about how particles and sub particles settle in the lowest energy state. With our conjuncture of fractional charge quantization, the shape of the energy profile and energy eigenvalues above the surface of quasi particle nature of an electron quanta in chromotized water sample (confirmed with absorption and Fourier transform inferred (FTIR) spectroscopies) is verified. The other results of energy profiles such as on the surface and inside the surface of quasi particle behaviour of an electron quanta will decipher new physics for understanding the complex nature of exchange energy fields, may be the intermediatory nature of strong forces in the nucleus of the atom due to quarks.
Cite this paper
SaleemIqbal,FarhanaSarwar,Syed MohsinRaza, (2016) Eigenfunctions for a Quantum Wire on a Single Electron at Its Surface and in the Quantum Well with Beaded Fractional Quantized States for the Fractional Charges. Journal of Applied Mathematics and Physics,04,320-327. doi: 10.4236/jamp.2016.42039
References
- 1. Griffths, D.J. (2005) Introduction to Quantum Mechanics. 2/e, Pearson Education.
- 2. Liboff, R.L. (2003) Introduction to Quantum Mechanics. 4/e, Pearson Education.
- 3. Gasiorowicz, S. (2003) Quantum Mechanics. 3/e, John Wiley, New York.
- 4. Gormani, M., Rehman, F., Ahmed, M.A. and Raza, S.M. (2006) Quantum Behaviour of Dielectric in Dolomite of Balochistan, Pakistan. Journal of the Chemical Society of Pakistan, 28, 414-416.
- 5. Yousaf, S., Raza, S.M., Masoom, Y. and Mujeeb, U.R. (2008) Absorption of Radiant Energy in Water: A New Conjecture and Theory of Charge Quantization in Chromotized Water Samples. Science International Lahore. Pakistan, 20, 189-195.
- 6. Yousaf, S., Raza, S.M. and Ahmed, M.A. (2008) Newly Developed Recursive Relationship for Fractional Quantum States and Associated Energy Eigen Values. Science International Lahore. Pakistan, 20, 255-260.
- 7. Yousaf, S., Raza, S.M., Masoom, Y. and Mujeeb, U.R. (2009) Quantum Theory of Dielectric and Its Applications to Dolomite of Balochistan, Pakistan. Science International Lahore. Pakistan, 21, 29-32.
- 8. Iqbal, S., Sarwar, F., Raza, S.M. and Rehman, A. (2015) How Fractional Charge on an Electron in the Momentum Space Is Quantized? ASRJETS, 14, 265-272.
- 9. Iqbal, S. (2012) PhD Thesis Analysis and Applications of Fractional Fourier Transform. Unpublished, University of Balochistan, Quetta.