Received 10 December 2015; accepted 24 January 2016; published 27 January 2016

ABSTRACT

In this paper, pursuing a new advised method called Delta method which is basically similar to variational method, we find the ground and excited states, according to a typical quantum Hamiltonian. Moreover, applying this method, the upper bound values for the eigenenergies of the so- called ground and excited states are estimated. We will show that this new method, is as beneficial as the traditional variational method which is common in deriving eigenenergies of some of the quantum Hamiltonians. This method helps physics students to broaden their knowledge about the possible mathematical ways; they can use to obtain eigenenergies of some quantum Hamiltonians. The advantage of Delta method to variational method is in its simplicity and reduction of the calculation procedures.

Keywords:

Quantum Mechanics, Eigenenergies, Alternative Methods, Delta Method

1. Introduction

Most problems encountered in quantum mechanics cannot be solved exactly. Exact solutions of the Schrodinger equation exist only for a few idealized systems. So, in order to solve general problems, one must resort to approximation methods. Up to now, a variety of such methods have been developed, and each has its own area of applicability. There are many methods for solving Schrodinger equation, i.e. perturbation theory [1] , the variational method [1] , and the WKB method [1] , Supersymmetry quantum mechanics [2] - [6] , Nikivorov-Uvarov method [7] - [9] , Romanovski polynomials in quantum mechanics [10] - [12] , etc. [12] - [23] .

Three conventional approximation methods for studying the stationary states corresponding to time-indepen- dent Hamiltonians, are: perturbation theory, the variational method, and the WKB method. Perturbation theory is based on the assumption that the problem we wish to solve is, in some sense, only slightly different from a problem that can be solved exactly. In the case where the deviation between the two problems is small, perturbation theory is suitable for calculating the contribution associated with this deviation; this contribution is then added as a correction to the energy and the wave function of the exactly solvable Hamiltonians. So perturbation theory builds on the known exact solutions to obtain approximate solutions.

But, about those systems whose Hamiltonians cannot be reduced to an exactly solvable part plus a small correction, the variational method or the WKB approximation are considered. The variational method is particularly useful in estimating the energy eigenvalues of the ground state and the first few excited states of a system for which one has only a qualitative idea about the form of the wave function. The WKB method is useful for finding the energy eigenvalues and wave functions of systems for which the classical limit is valid. Unlike perturbation theory, the variational and WKB methods do not require the existence of a closely related Hamiltonian that can be solved exactly [1] .

The application of the approximation methods to the study of stationary states consists of finding the energy eigenvalues 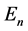and the eigenfunctions 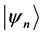of a time-independent Hamiltonian 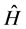that does not have exact solutions:

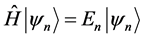
Depending on the structure of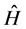, we can use any of the three methods mentioned above to find the approximate solutions to this eigenvalue problem.

In this paper, we will use a new approximation method called Delta method for finding the ground and excited energy state of stationary states. This method, with a difference in the way of calculation, is somehow similar to the variational method at the beginning. Like the variational method, we first find the time-independent Hamiltonian 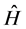that does not have exact solution, using a supposed trial function and calculating the value of energy 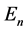in terms of a parameter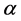. Then, we will estimate the upper bound values for the eigenenergies of ground and excited states applying the Delta conditions 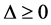and 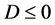on the second and third order equations, respectively. The difference between Delta and variational methods is that in variational method the derivative of E to 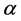is calculated and the solution for 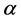is obtained with affecting the conditions on E. But, in Delta method, we obtain the physical solutions with writing 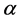in terms of E in the form of a two or three order equation and applying the mathematical Delta conditions. Moreover, in variational method, after calculating the derivative of E to 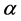and equating it with zero to find the 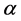which minimizes, i.e. in Hydrogen atom, sometimes one of the solutions for is infinite which is an unphysical solution, since it leads to a zero value for the ground or excited state energy. While, in delta method, only the physical solution is attained.

It should be noted that Delta method could be applied to all of the problems to be solved through variational method and exactly give the same result. However, the advantage of Delta method is first in its simplicity, and then in reduction of the calculation procedures.

In Section 2, we will have a review on the variational method [1] . In Section 3, we will explain Delta method and in Section 4, we will show the applicability and simplicity of Delta method with some examples.

2. Variational Method

There exist systems whose Hamiltonians are known, but they cannot be solved exactly or by a perturbative treatment. That is, there is no closely related Hamiltonian that can be solved exactly or approximately by perturbation theory because the first order is not sufficiently accurate. One of the approximation methods that are suitable for solving such problems is the variational method, which is also called the Rayleigh-Ritz method. This method does not require knowledge of simpler Hamiltonians that can be solved exactly. The variational method is useful for determining upper bound values for the eigenenergies of a system whose Hamiltonian is known whereas its eigenvalues and eigenstates are not known. It is particularly useful for determining the ground state. It becomes quite cumbersome to determine the energy levels of the excited states.

In the context of the variational method, one does not attempt to solve the eigenvalue problem:

(1)

But rather one uses a variational scheme to find the approximate eigenenergies and eigenfunctions from the variational equation:

(2)

where is the expectation value of the energy in the state:

(3)

If depends on a parameter, will also depend on. The variational ansatz (2) enables us to vary so as to minimize. The minimum value of provides an upper limit approximation for

the true energy of the system. The variational method is particularly useful for determining the ground state energy and its eigenstate without explicitly solving the Schrodinger equation. Not that for any (arbitrary) trial function we choose, the energy E as given by (3) is always larger than the exact energy:

(4)

The equality condition occurs only when is proportional to the true ground state. Because, expanding the trial function in terms of the exact eigenstates of:

(5)

with

(6)

and since for nondegenerate one-dimensional bound systems, we have:

(7)

which proves (4).

To calculate the ground state energy, we need to carry out the following four steps:

・ First, based on physical intuition, make an educated guess of a trial function that takes into account all the physical properties of the ground state (symmetries, number of nodes, smoothness, behavior at infinity, etc.). For

the properties we are not sure about, they can be included in the trial function adjustable parameters (i.e.,) which will account for the various possibilities of these unknown properties.

・ Second, using (3), calculate the energy; this yields an expression which depends on the parameters :

(8)

In most cases will be assumed to be normalized; hence the denominator of this expression is equal to 1.

・ Third, using (8) search for the minimum of by varying the adjustable parameters until is minimized. That is, minimize with respect to :

(9)

with. This gives the values of that minimize.

・ Fourth, substitute these values of into (8) to obtain the approximate value of the energy. The value of thus obtained, provides an upper bound for the exact ground state energy. The exact ground state eigenstate will then be approximated by the state.

About the energies of the excited states, it should be said that the variational method can also be used to find the approximate values for the energies of the first few exited states. For instance, to find the energy and eigenstate of the first excited state that will approximate and, we need to choose a trial function that must be orthogonal to:

(10)

Then proceed as we did in the case of the ground state. That is, solve the variational Equation (2) for:

(11)

Similarly, to evaluate the second excited state, we solve (2) for and take into account the following two conditions:

(12)

These conditions can be included in the variational problem by means of Lagrange multipliers, that is, by means of a constrained variational principle.

In this way, we can in principle evaluate any other excited state. However, the variational procedure becomes increasingly complicated as we deal with higher excited states. As a result, the method is mainly used to determine the ground state.

3. Delta Method

In this section, we obtain the expectation value of energy in a supposed state, like the variational method, depends on a parameter, and finally will depend on, too. Then, instead of minimizing leading to a minimum value of as an upper approximate limit for the real energy of system, we use a new method in which we write the expectation value of energy in a supposed state in the form of a second order equation in terms of, i.e., and using the method of finding the solution of a second order equation, we calculate and then, write in terms of, so that we have:

(13)

where are constants and the term will be a function of E. For having a solution for in terms of E, we should have:

(14)

Then, using this inequality, just like the variational method, an upper limit for energy is obtained that leads to finding the approximate value of ground or excited state energy.

In some of the problems, the expectation value of energy in terms of leads to a third order equation in terms of E in the form of using which by writing the required conditions for having real roots of in terms of E, one can find the desired solutions, i.e. the ground or excited state energy. Writing the required conditions for solving third order equation, we first write the parameters as the following:

(15)

(16)

(17)

Now, according the sign of, the solutions for the third order equation are obtained as:

(18)

(19)

Then, three distinct real solutions are obtained for in terms of E. Moreover:

(20)

(21)

then, one real solution and two complex solutions are obtained [24] . Of course, since in physical problems is a real scale factor, so without the need for calculating in terms of E, it is sufficient to apply the Delta conditions and on the second and third order equations respectively, and estimate the ground or excited state energies. It should be noted that the reason for using the condition is to ensure the real solutions. This method can be applied for higher order equations in terms of, too.

In the next section, we will consider a few examples of quantum mechanics and estimate their upper limit of the ground or excited state energies, using Delta method. We remark that this method can be applied as another approach to approximate solutions for all the problems of quantum mechanics to be solved through the variational method. In the case of selecting a suitable trial function, Delta method can be applied to a complex problem such as Poschl-Teller, Rosen-Morse, or another shape invariant potential in quantum mechanics, too. However, the main point is that proposing and guessing the suitable trial function which is based on physical intuition, is very important. For example, it can be shown that with some proposal trial wave functions and applying some simplification, exactly the same result could be achieved for Poschl-Teller and Rosen-Morse potentials through both variational and Delta methods. Of course, it should be noted that up to now, a variety of approximation methods have been developed, and each has its own area of applicability. However, the main purpose of introducing Delta method is to show that this new method, is as beneficial as the traditional variational method which is common in deriving eigenenergies of some of the quantum Hamiltonians, and to help physics students to broaden their knowledge about the possible mathematical ways to obtain eigenenergies of some quantum Hamiltonians with a simpler method than the conventional variational method.

4. Examples

In this section, using Delta method, we estimate the upper limit of the ground or excited state energies for a few examples of quantum mechanics that are obtained from the variational method, before.

Exp. 1

Calculating the ground and excited state energies of a one-dimensional harmonic oscillator using Delta method.

Choosing the trial function for ground state in the form of and writing the expectation value of E₀ in terms of:

Neglecting the calculations, we get:

In Delta method there is no need for obtaining the derivative of to. It is just sufficient to form the second order equation for in terms of E:

Using the Delta method, the solutions for will be:

As it can be seen, is an upper limit for which is the value of the ground state energy. For obtaining the excited state energy, writing the trial function in the form of, we have:

Again, forming the second order equation of in terms of, we get:

and then,

which is the same value obtained from the variational method.

Exp. 2

Estimating the ground state energy of the Hydrogen atom using Delta method.

Choosing the trial function in the form of, where is a scale factor, energy is obtained as:

Now, using Delta method we have:

that is the same estimated value for the ground state energy of the Hydrogen atom obtained from the variational method.

We should note that if we find for Hydrogen atom through variational method with the same trial function:

we find that one of the solutions for is infinite which is an unphysical solution, since it leads to a zero value for the ground or excited state energy. While, in Delta method, only the physical solution is attained.

Exp. 3

Estimation of the ground state energy of a one-dimensional harmonic oscillator by making use of Delta method with the following two trial functions:

(a)

(b)

where is a positive real number and A is the normalization constant.

(a) We have:

The final solution is:

or

,

which is the ground state energy of a one-dimensional harmonic oscillator with the above defined trial function and is the same result obtained from the variational method.

(b) We have:

therefore

Again, it is quite in accordance with the resulted solution of variational method.

Exp. 4

Applying Delta method, we calculate the ground state energy for a particle of mass m which is bouncing vertically and elastically on a reflecting hard floor where and g is the gravitational constant.

Choosing the trial function, where is a parameter and A is the normalization constant, we can show and therefore:

.

In the above third order equation of in terms of, using Equations (2) to (8) we have:

The third order equation has some defined solutions due to or or. The physical solution is obtained for as:

which is consistent with the solution obtained from variational method, i.e.

.

Exp. 5

Estimation of the ground state energy and the corresponding wave function of a system consisting of two identical particles of spin that are confined to an isotropic three-dimensional harmonic oscillator potential of frequency , using delta method, when the two particles do not interact.

Choosing the trial function in the form of, we have:

Applying Delta method, we get:

which with

we will encounter the following condition:

,

that is the same energy of the ground state obtained from the variational method.

5. Conclusion

In this paper, we used an alternative method of finding the ground and excited energies state of stationary states. Basically, it is the same as the variational method, where a time-independent Hamiltonian with no exact solution is exploited, however, in this new method, we used a trial function and calculated the value of energy in terms of a defined parameter. Therefore, the estimation of the upper bound values and the excited state energies, is based on applying the Delta conditions and, which are included respectively, in appropriate second and third order equations. Presenting some examples, we showed that the corresponding results which have been obtained within this new method are in consistence with those derived from the traditional variational method. It is remarkable that all the problems to be solved through variational method, could be solved through Delta method and lead to exactly the same result with the difference that Delta method is simpler and the calculation procedures are less than that of the variational method.

Cite this paper

FarrinPayandeh,TourajMohammadpour, (2016) Calculation of the Approximate Energy of Ground and Excited Stationary States in Quantum Mechanics Using Delta Method. Journal of Applied Mathematics and Physics,04,130-139. doi: 10.4236/jamp.2016.41016

References