Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61503,11 pages
10.4236/jamp.2015.311172
Exact Solution of Second Grade Fluid in a Rotating Frame through Porous Media Using Hodograph Transformation Method
Sayantan Sil1, Manoj Kumar2
1Department of Physics, S.S.L.N.T. Mahila College, Dhanbad, India
2Post Graduate Department of Physics, Ranchi College, Ranchi, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 7 October 2015; accepted 23 November 2015; published 26 November 2015

ABSTRACT
In this paper exact solution for a homogenous incompressible, second grade fluid in a rotating frame through porous media has been provided using hodograph-Legendre transformation method. Results are summarised in the form of theorems. Two examples have been taken and streamline patterns are shown for the solutions.
Keywords:
Non-Newtonian Fluid, Rotating Frame, Hodograph Transformation, Porous Media, Exact Solution

1. Introduction
Many phenomena which are closer to our daily lives like atmospheric or oceanic circulations, hurricanes and tornados, bath tub vorticities, stirring tea in a cup are all examples of rotating fluids. The theory of rotating fluids has become very important because of its occurrence in many natural phenomena for its application in various technological solutions which are directly governed by the action of Coriolis forces due to earth’s rotation. Many studies have been made on the rotating fluid and several investigations have been carried out on various types of flows both non-MHD and MHD in a rotating system. Jana and Dutta [1] studied “Couette flow” in a rotating system. Vidyanidhu and Nigam [2] analyzed the “Poiseuille flow” in a rotating system. Soundalgekar and Pop [3] and Gupta [4] studied injection/suction effects for the case of rotating horizontal porous plates. Bagewadi and Siddabassapa [5] [6] , Singh, Singh and Rambabu [7] , Singh and Tripathi [8] , Singh and Singh [9] , Thakur and Manoj Kumar [10] studied rotating MHD flow and found out exact solutions. Krishan Dev Singh [11] studied unsteady MHD Poiseuille flow in a rotating system. M.A. Imran et al. [12] found out exact solutions for the MHD second grade fluid in a porous medium using integral transformation technique. A.M. Rashid [13] studied unsteady MHD flow of a rotating fluid from stretching surface in porous medium and effects of radiation and variable viscosity on it. Sayantan Sil and Manoj Kumar [14] studied rotating orthogonal plane MHD flow through porous media using complex variable technique.
The role of non-Newtonian fluids has become very important these days due to modern technological and industrial applications. Increasing emergence of non-Newtonian fluids such as molten plastic pulp, emulsions, raw materials in great varieties of industries like petroleum and chemical processes has stimulated a considerable amount of interest in the study of behaviour of such fluids in motion. Also the flow of non-Newtonian fluids has various technological applications including plastic manufacture, performance of lubricants, applications of paints, processing of food and movement of biological fluids. In the studies of non-Newtonian fluids not only the non-linearities increase considerably, in comparison to the non-linearities occurring in the inertia part of the Navier-Stokes equations, but in certain cases the order of differential equation also increase. In case of a homogenous incompressible fluid of second grade, it is found that the governing equations are, in general, of third order, as compared to the second order Navier-Stokes equations [15] [16] . For obtaining exact solutions transformation techniques involving inverse or semi-inverse methods are used for reformulation of equations in solvable form. Following Martin’s formulation [17] some researchers have used hodograph transformation [18] in order to linearise the system of governing equations and got some exact solutions. This method has been widely used and W.F. Ames [18] has given an excellent survey to this method together with applications to various other fields. Hodograph transformation method is used in various fields of research such as gas dynamics [19] [20] , linear viscous fluids [21] , non-Newtonian fluids [22] [23] and MHD Newtonian and non-Newto- nian fluid flows [15] [24] . Chandna, Barron and Smith [21] applied hodograph transformation in steady plane flow. Chandna and Garg [16] used this technique to study viscous incompressible orthogonal flow. Baron and Chandna [25] used this method to study constantly inclined incompressible plane flows. Chandna, Barron and Chew [26] used this method to study variably inclined incompressible MHD plane flow. Chandna and Nguyen [15] used this approach to study non-Newtonian MHD transverse fluid flows. Siddiqui, Kaloni and Chandna [22] used this method to study incompressible second grade fluid. Singh and Mishra [27] used this technique to study steady plane MHD flows. Thakur and Mishra [28] applied this method to rotating hydromagnetic flows. Singh and Tripathi [29] used hodograph transformation to find exact solutions for plane rotating MHD flow with orthogonal magnetic and velocity field. Siddiqui, Hayat, Siddiqui and Asghar [30] used this technique to study unsteady plane viscous flow. Mishra and Mishra [31] used hodograph transformation in unsteady MHD transverse flows. Sayantan Sil, Manoj Kumar and Thakur [32] applied hodograph transformation to MHD transverse fluid flows through porous media. Recently Manoj Kumar [33] studied non-Newtonian fluid flows through porous media applying hodograph transformation method.
Flow of fluid through porous medium is of interest to a wide range of engineers and and scientists, in addition to economists who recognise the importance of ground water flows and variety of tertiary oil recovery processes. There are numbers of practical applications of fluid flow through porous medium, including filtration flow in packed column, permeation of water or oil within matrix of porous rock etc. Many researchers have studied the flow of various fluids through porous media. Ram and Mishra [34] have studied unsteady MHD flow through a porous medium in a circular pipe under action of constant pressure gradient. Singh and Singh [8] discussed the problem of steady plane MHD flow through porous media. Thakur and Singh [35] studied steady plane variably inclined MHD flows through porous media applying magnetograph transformations. Thakur, Manoj Kumar and Mahan [36] studied steady MHD orthogonal plane fluid flows through porous media. Also Bhatt and Shirley [37] applied hodograph transformation method in plane viscous flow in porous media.
2. Basic Equations
The basic equations governing the motion of homogenous, incompressible, second-grade fluid in a rotating frame through porous media are
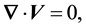 (1)
(1)
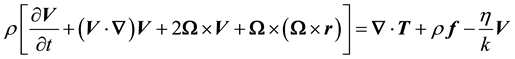 , (2)
, (2)
and the constitutive equation for the Cauchy stress T,
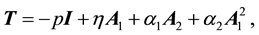 (3)
(3)
where V = velocity field vector, p = dynamic pressure function,
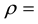 the constant fluid field density,
the constant fluid field density,
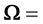 angular velocity vector, r = radius vector,
angular velocity vector, r = radius vector,
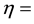 coefficient of dynamic viscosity,
coefficient of dynamic viscosity,
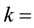 permeability of the medium and
permeability of the medium and
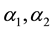 are the normal stress moduli. ?pI denotes the deterninate spherical stress,
are the normal stress moduli. ?pI denotes the deterninate spherical stress,
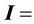 isotropic tensor, so that
isotropic tensor, so that
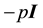 becomes
becomes
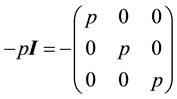 .
.
The Rivlin-Ericksen tensors A1 and A2 are defined as
 ,
,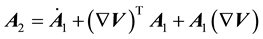 , (4)
, (4)
where a dot over A1 denotes the material time derivative.
If we substitute (3) in (2) and make use of (4) we get
 (5)
(5)
where
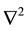 denotes the Laplacian ,
denotes the Laplacian ,
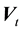 denotes the partial derivative of
denotes the partial derivative of





In the case of steady plane flow in a rotating frame through porous media when body forces are absent, (1) and (5) reduce to



Equations (6)-(8) form three partial differential equations for three unknowns u, v,
Let us define the two-dimensional vorticity function



where

Employing (9) and (10) in (7) and (8) we obtain the following system of equations:




The above system of four partial differential equations in four unknown functions u, v,


3. Equations in Hodograph Plane
Letting the function



we may consider x and y as functions of u and v. By means of


We also obtain the relations

where


Employing these transformation relations for the first order partial derivatives and the transformation equations for the functions

the system of Equations (11) is replaced by the following system in the hodograph plane (u, v):




where,

System of Equations (16) to (19) is a system of four equations for the four unknown functions



The equation of continuity implies the existence of a stream-function


Likewise Equation (16) implies the existence of a function L(u, v) , called the Legendre transform function of the stream-function

and the two functions

Introducing L(u, v) in the system (16)-(19), with j, w1, w2, given by (15), (20) respectively, it follows that (16) is identically satisfied and the system may be replaced by



where

By using the integrability condition
i.e.



where j, w1, w2 are given in (26) and (27) . Summing up we have the following theorem:
THEOREM I: If





4. Application I
Let

be the Legendre-transform function, where A, B are arbitrary non zero constants and

Now employing (29) and (30) in Equation (27), we find that


The above Equation (31) is satisfied only for

Using


Using




mined to be

where

Figure 1 shows that the streamlines of the flow equations are concentric hyperbolas.
THEOREM II: If

Figure 1. Concentric hyperbolic streamlines.
plane, incompressible, second-grade fluid flows in a rotating frame through porous media, then the flow in the physical plane is a flow with concentric hyperbolic streamlines with flow variables given by (33) and (34).
5. Application II
Let

be the Legendre- transform function with

Using (35) in (26) and (27), we find that

On substituting (36) in (28), we find that


The above equation (37) is satisfied if

On proceeding as in Application I, we get

and

where

Figure 2 shows that the streamlines of the flow equations are rectangular hyperbolae.
Figure 2. Rectangular hyperbolae streamlines.
THEOREM III: If

In the absence of rotating reference frame i.e.

when porous media is absent i.e. the term

O.P Chandna [22] .
6. Conclusion
In this paper, the analytical solution of nonlinear equations governing the flow of second grade fluid in a rotating frame through porous media is obtained using transformation technique. Illustrations have been made taking different forms of Legendre transform function. The expressions for velocity profile, streamline and pressure distribution are constructed in each case. Streamline patterns are also plotted. Our results indicate that pressures are dependent upon material parameters α1 and α2 of the second grade fluid. Also, the present analysis is more general and several results of various authors (as already mentioned in the text) can be recovered in the limiting cases.
Cite this paper
SayantanSil,ManojKumar, (2015) Exact Solution of Second Grade Fluid in a Rotating Frame through Porous Media Using Hodograph Transformation Method. Journal of Applied Mathematics and Physics,03,1443-1453. doi: 10.4236/jamp.2015.311172
References
- 1. Jana, R.N. and Dutta, N. (1977) Couette Flow and Heat Transfer in a Rotating System. Acta Mechanica, 26, 301-306.
http://dx.doi.org/10.1007/BF01177152 - 2. Vidyanidhu, V. and Nigam, S.D. (1967) Secondary Flow in a Rotating Channel. Journal of Mathematical and Physical Sciences, 1, 85-100.
- 3. Soundalgekar, V.M. and Pop, I. (1973) On Hydromagnetic Flow in a Rotating Fluid Past an Infinite Porous Wall. Journal of Applied Mathematics and Mechanics, ZAMM, 53, 718-719.
http://dx.doi.org/10.1002/zamm.19730531012 - 4. Gupta, A.S. (1972) Ekman Layer on a Porous Plate. Physics of Fluids, 15, 930-931.
http://dx.doi.org/10.1063/1.1694002 - 5. Bagewadi, C.S. and Siddabasappa (1993) Study of Variably Inclined Rotating MHD Flows in Magnetograph Plane. Bulletin of the Calcutta Mathematical Society, 85, 93-106.
- 6. Bagewadi, C.S. and Siddabasappa (1993) The Plane Rotating Viscous MHD Flows. Bulletin of the Calcutta Mathematical Society, 85, 513-520.
- 7. Singh, S.N., Singh, H.P. and Rambabu (1984) Hodograph Transformations in Steady Plane Rotating Hydromagnetic Flow. Astrophysics and Space Science, 106, 231-243.
http://dx.doi.org/10.1007/BF00650351 - 8. Singh, K.K. and Singh, D.P. (1993) Steady Plane MHD Flows through Porous Media with Constant Speed along Each Stream Line. Bulletin of the Calcutta Mathematical Society, 85, 255-262.
- 9. Thakur, C. and Kumar, M. (2008) Plane Rotating Viscous MHD Flows through Porous Media. Pure and Applied Mathematika Sciences, LXVII, 113-124.
- 10. Singh, H.P. and Tripathi, D.D. (1988) A Class of Exact Solutions in Plane Rotating MHD Flows. Indian Journal of Pure and Applied Mathematics, 19, 677-687.
- 11. Singh, K.D. (2013) Rotating Oscillatory MHD Poisseuille Flow: An Exact Solution. Kragujevac Journal of Science, 35, 15-25.
- 12. Imran, M.A., Imran, M. and Fetecau, C. (2014) MHD OSCILLATING Flows of a Rotating Second Grade Fluid in Porous Medium. Communication in Numerical Analysis, 2014, Article ID: cna-00196.
www.ispacs.com/journals/cna/2014/cna-00196/article.pdf - 13. Rashid, A.M. (2014) Effects of Radiation and Variable Viscosity on Unsteady MHD Flow of a Rotating Fluid from Stretching Surface in Porous Media. Journal of Egyptian Mathematical Society, 2, 134-142.
http://dx.doi.org/10.1016/j.joems.2013.05.008 - 14. Sil, S. and Kumar, M. (2014) A Class of Solution of Orthogonal Plane MHD Flow through Porous Media in a Rotating Frame. Global Journal of Science Frontier Research: A Physics and Space Science, 14, 17-26.
https://globaljournals.org/GJSFR_Volume14/E-Journal_GJSFR_%28A%29_Vol_14_Issue_7.pdf - 15. Chandna, O.P. and Nguyen, P.V. (1989) Hodograph Method in Non-Newtonian MHD Transverse Fluid Flows. Journal of Engineering Mathematics, 23, 119-139.
http://dx.doi.org/10.1007/BF00128864 - 16. Chandna, O.P. and. Garg, M.R (1979) On Steady Plane Magnetohydrodynamic Flows with Orthogonal Magnetic and Velocity Field. International Journal of Engineering Science, 17, 251-257.
http://dx.doi.org/10.1016/0020-7225(79)90088-0 - 17. Martin, M.H. (1971) The Flow of Viscous Fluid. Archive for Rational Mechanics and Analysis, 41, 266-286.
http://dx.doi.org/10.1007/BF00250530 - 18. Ames, W.F. (1965) Non-Linear Partial Differential Equations in Engineering. Academic Press, New York.
- 19. Ghaffari, A.G. (1950) The Hodograph Method in Gas Dynamics. Tehran Taban Press, Tehran.
- 20. Cherry, T.M. (1961) Trans-Sonic Nozzle Flows Found by the Hodograph Method. In: Langer, R.E., Ed., Partial Differential Equations and Continuum Mechanics, University of Wisconsin Press, Madison, 216-232.
- 21. Chandna, O.P., Barron, R.M. and Smith, A.C. (1982) Rotational Plane Steady Flows of a Viscous Fluid. SIAM Journal on Applied Mathematics, 42, 1323-1336.
http://dx.doi.org/10.1137/0142092 - 22. Siddiqui, A.M., Kaloni, P.N. and Chandna, O.P. (1985) Hodograph Transformation Methods in Non-Newtonian Fluids. Journal of Engineering Mathematics, 19, 203-216.
http://dx.doi.org/10.1007/BF00042534 - 23. Moro, L., Siddiqui, A.M. and Kaloni, P.N. (1990) Steady Flows of a Third-Grade Fluid by Transformation Methods. ZAMM, 70, 189-198.
http://dx.doi.org/10.1002/zamm.19900700309 - 24. Swaminathan, M.K., Chandna, O.P. and Sridhar, K. (1983) Hodograph Study of Transverse MHD Flows. Canadian Journal of Physics, 61, 1323-1336.
http://dx.doi.org/10.1139/p83-134 - 25. Barron, R.M. and Chandna, O.P. (1981) Hodograph Transformation and Solutions in Constantly Inclined Plane Flows. Journal of Engineering Mathematics, 15, 211-220.
http://dx.doi.org/10.1007/BF00042781 - 26. Chandna, O.P., Barron, R.M. and Chew, K.T. (1982) Hodograph Transformations and Solutions in Variably Inclined MHD Plane Flows. Journal of Engineering Mathematics, 16, 223-243.
http://dx.doi.org/10.1007/BF00042718 - 27. Singh, H.P. and Mishra, R.B. (1987) Legendre Transformation in Steady Plane MHD Flows of a Viscous Fluid. Indian Journal of Pure and Applied Mathematics, 18, 100-109.
- 28. Thakur, C. and Mishra, R.B. (1988) On Steady Plane Rotating Hydromagnetic Flows. Astrophysics and Space Science, 146, 89-97.
http://dx.doi.org/10.1007/BF00656985 - 29. Singh, S.N. and Tripathi, D.D. (1987) Hodograph Transformations in Steady Plane Rotating MHD Flows. Applied Scientific Research, 43, 347-353.
http://dx.doi.org/10.1007/BF00540568 - 30. Siddiqui, A.M., Hayat, T., Siddiqui, J. and Asghar, S. (2008) Exact Solutions of Time-Dependent Navier-Stokes Equations by Hodograph-Legendre Transformation Method. Tamsui Oxford Journal of Mathematical Sciences, 24, 257-268.
- 31. Mishra, P. and Mishra, R.B. (2010) Hodograph Transformations in Unsteady MHD Transverse Flows. Applied Mathematical Sciences, 56, 2781-2795.
- 32. Sil, S., Kumar, M. and Thakur, C. (2012) Solutions of Non-Newtonian MHD Transverse Fluid Flows through Porous Media. Proceedings of the 57th Congress of ISTAM, Defence Institute of Advanced Technology, Pune, 17-20 December 2012, 13-21.
- 33. Kumar, M. (2014) Solution of Non-Newtonian Fluid Flows through Porous Media by Hodograph Transformation Method. Bulletin of Calcutta Mathematical Society, 106, 239-250.
- 34. Ram, G. and Mishra, R.S. (1977) Unsteady MHD Flow of Fluid through Porous Medium in a Circular Pipe. Indian Journal of Pure and Applied Mathematics, 8, 637-647.
- 35. Thakur, C. and Singh, B. (2000) Study of Variably Inclined MHD Flows through Porous Media in Magnetograph Plane. Bulletin of Calcutta Mathematical Society, 92, 39-50.
- 36. Thakur, C., Kumar, M. and Mahan, M.K. (2006) Exact Solution of Steady MHD Orthogonal Plane Fluid Flows through Porous Media. Bulletin of Calcutta Mathematical Society, 98, 583-596.
- 37. Bhatt, B. and Shirley, A. (2008) Plane Viscous Flows in Porous Medium. Matematicas: Ensenanza Universitaria, XVI, 51-62.










