Journal of Applied Mathematics and Physics
Vol.03 No.10(2015), Article ID:60743,7 pages
10.4236/jamp.2015.310159
Finite Temperature Asymmetric Nuclear Matter Using Pion Dressing
Saroj Kumar Sahu
Department of Physics, Banki College (Autonomous), Cuttack, India
Email: saroj9a@yahoo.co.in
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 September 2015; accepted 26 October 2015; published 29 October 2015
ABSTRACT
We study the asymmetric nuclear matter in a nonperturvative manner at finite temperatures using thermofield dynamics method. The nucleon-meson interaction is taken to examine the binding energy (EB), pressure (P) for various proton fractions.
Keywords:
Binding Energy, Equation of State, Pion Dressing, Hot Dense Nuclear Matter

1. Introduction
The properties of hot dense nuclear matter are very important in the context of neutron stars [1] as well as in high-energy heavy-ion collisions experiments. In those experiments, nuclei undergo collisions [2] and produce states of nuclear matter at different temperatures at conditions far from those normally encountered in low energy collisions. At low temperatures, this can be attained in medium energy heavy-ion reactions; no such exotic state can be produced but there is the possibility of interesting liquid-gas phase transitions leading to the breakup of heated nuclei into small clusters or droplets of nucleons [3] .
Such phase transitions have been identified in multifragmentation experiments and in the crusts of neutron stars [4] [5] . The possibilities of such phase transitions were previously considered by several authors using different approaches [6] - [8] . Walecka [9] in a attempt, developed a method consisting of interactions of nucleons with a neutral scalar field σ and ρ mesons as well as neutral vector meson ω. Variations of the same model have also been considered including cubic and quartic terms in the σ fields to reproduce correct bulk modulus of nuclear matter [10] . These calculations however use meson fields as classical, and use a σ-field which is not observed.
A model for infinite nuclear matter consisting of interacting nucleons and pions was considered in [11] . The Pion Nucleon interaction was taken with off mass shell of pion. The scalar isoscalar pion condensates simulated the effects of σ mesons [12] with the short distance repulsion arising from composite structure of nucleons and/or through vector meson exchanges. This appeals aesthetically as classical σ fields arise from quantum mechanical structures and also has a stronger phenomenological appeal as σ mesons have not been found in nature. With a similar approach we shall reconsider nuclear matter at finite temperatures with pion dressing [13] with off mass shell. The methods of thermofield dynamics [14] fit naturally for this purpose because here statistical average is done through an expectation value over a “thermal vacuum” [11] in an extended Hilbert space.
The article is organised as follows. In Section 2, we review the thermofield dynamics to consider hot and dense nuclear matter and obtain expressions for temperature-dependant pressure P, binding energy B and nuclear density ρ. In Section 3, we evaluate numerically the above applying variational technique, study their characteristics and discuss the results so obtained.
2. Formalism
We consider the effective Hamiltonian for pion nucleon interaction at zero temperature [15] -[17] as
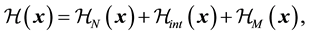 (1)
(1)
where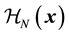 ,
,
 and
and
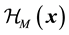 are the Hamiltonians for the free nucleon part, the pion-interaction part and the free meson part respectively. Here
are the Hamiltonians for the free nucleon part, the pion-interaction part and the free meson part respectively. Here
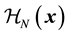 is given by
is given by
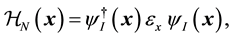 (2)
(2)
and the effective Hamiltonian
 for pion nucleon
for pion nucleon
 interaction
interaction
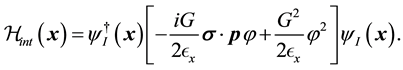 (3)
(3)
We have taken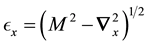 , with M as the mass of the nucleon. The free meson part of the Hamiltonian is given by
, with M as the mass of the nucleon. The free meson part of the Hamiltonian is given by
 (4)
(4)
where
 denotes the mass of the meson and
denotes the mass of the meson and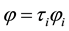 . The pion field expansion in Equation (4) in terms of annihilation and creation operators is given by
. The pion field expansion in Equation (4) in terms of annihilation and creation operators is given by
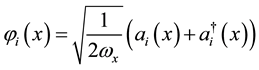
 (5)
(5)
with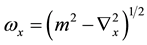 . We now study asymmetric nuclear matter at finite temperature using thermofield dynamics method. Here the thermal average of a quantum operator
. We now study asymmetric nuclear matter at finite temperature using thermofield dynamics method. Here the thermal average of a quantum operator



The above reduces to ground state expectation, in zero temperature limit value for the operator

where



where




where



where
For zero chemical potential and for free fields, extremization of the free energy then yields

with Hamiltonian density as

If we substitute this value the free energy density becomes
Similarly for the fermionic sector the thermal vacuum is

where

and


where



with

and

In the above,

In nucleon sector for fermions

with

where


Here the thermodynamic potential [18] is given by

where









The temperature dependent kinetic energy due to the mesons is given by

where



where

we shall now assume a phenomenological term corresponding to meson repulsion due to composite structure of mesons given as

Finally, the nucleon repulsion term given as

where


where
as before.
The thermodynamic potential density Ω is given by

where the last term corresponds to nucleon number conservation with





and similarly the meson sector contribution

Thus the thermodynamic potential density now is a functional of




which is of the same form as [16] for zero temperature. Similarly minimising the thermodynamic potential with respect to


where

Once we substitute the optimised dressing as in Equation (30), the above simplifies to

which is different from



with

where J is given in Equation (25). We may note that the change in


3. Results and Discussions
The parameters a,




compressibility K of the symmetric nuclear matter i.e.


The fourth parameter


The pion-nucleon coupling constant




In Figure 1 we study the nature of variation of EB with different baryon densities at different temperatures. The saturation binding energy increases from −16 MeV at zero temperature to higher values with rise of temperature. This clearly shows that the temperature has a significant effect on symmetric nuclear matter.
In Figure 2, the variation of pressure P with nucleon densities have been studied at different temperatures (T = 0, 4, 8, 12, 16, 20 MeV). It shows that at the saturation density, the pressure is zero for zero temperature as usual. But pressure becomes negative if one goes towards lower density and it becomes zero at zero nuclear density. This peculear behaviour is first order phase transition. This trend disappears at higher temperatures.
In Figure 3, the variation of pressure with nucleon densities for different Proton fraction at different temperatures. It shows that at Proton fraction

Figure 1. The binding energy EB as a function of nucleon density ρ.
Figure 2. The pressure P as a function of nucleon density ρ at different temperature.
asymmetric nuclear matter behaves differently at different nucleon densities.
In Figure 4, the slope


temperatures for different proton fractions. It shows that the slope becomes negative as the relative nucleon densities increases to a certain value and then increases at higher values. The trend is same at different higher temperatures but terminates to a certain value of slope at certain lower densities.
4. Summary
In this paper, we study the warm equation of state (EOS) of asymmetric nuclear matter taking pion-nucleon interaction with repulsive effect due to ρ and ω mesons. We observe here that our results are comparable with the Non-Linear Walecka (NLWM) and Quark Meson Coupling (QMC) model [20] . The binding energy changes from negative to positive value with increase of temperature around saturation density. The profile of pressure variation with density at different temperatures shows that there is a liquid-gas phase transition and the transition
Figure 3. The pressure P as a function of nucleon density ρ for different proton fraction.
Figure 4. The pressure variation


is continuous above the critical temperature Tc at which
Cite this paper
Saroj KumarSahu, (2015) Finite Temperature Asymmetric Nuclear Matter Using Pion Dressing. Journal of Applied Mathematics and Physics,03,1308-1315. doi: 10.4236/jamp.2015.310159
References
- 1. Prakash, M., Bombaci, I., Prakash, M., Ellis, P.J., Lattimer, J.M. and Knorren, R. (1977) Composition and Structure of Protoneutron Stars. Physics Report, 280, 1-77.
http://dx.doi.org/10.1016/S0370-1573(96)00023-3 - 2. Abreu, M.C., et al. (2000) Evidence for Deconfinement of Quarks and Gluons from the J/ψ Suppression Pattern Measured in Pb-Pb Collisions at the CERN-SPS. Physics Letters B, 477, 28-36.
http://dx.doi.org/10.1016/S0370-2693(00)00237-9 - 3. Hauger, J.A., et al. (1996) Dynamics of the Multifragmentation of 1A GeV Gold on Carbon. Physical Review Letters, 77, 235.
http://dx.doi.org/10.1103/PhysRevLett.77.235 - 4. Pethick, C.J., Ravenhall, D.G. and Lorenz, C.P. (1995) The Inner Boundary of a Neutron-Star Crust. Nuclear Physics A, 584, 675-703.
http://dx.doi.org/10.1103/PhysRevLett.77.235 - 5. Lorenz, C.P., Ravenhall, D.G. and Pethick, C.J. (1993) Neutron Star Crusts. Physical Review Letters, 70, 379.
http://dx.doi.org/10.1103/PhysRevLett.70.379 - 6. Barranco, M. and Buchler, J.R. (1980) Thermodynamic Properties of Hot Nucleonic Matter. Physical Review C, 22, 1729. http://dx.doi.org/10.1103/PhysRevC.22.1729
- 7. Müller, H. and Serot, B.D. (1995) Phase Transitions in Warm, Asymmetric Nuclear Matter. Physical Review C, 52, 2072.
http://dx.doi.org/10.1103/PhysRevC.52.2072 - 8. Menezes, D.P. and Providencia, C. (1999) Droplet Formation in Cold Asymmetric Nuclear Matter. Nuclear Physics A, 650, 283-198.
http://dx.doi.org/10.1016/S0375-9474(99)00109-8Menezes, D.P. and Providencia, C. (1999) Nucleation Process in Asymmetric Hot Nuclear Matter. Physical Review C, 60, Article ID: 024313http://dx.doi.org/10.1103/physrevc.60.024313.
- 9. Walecka, J.D. (1974) A Theory of Highly Condensed Matter. Annals of Physics, 83, 491-529.
http://dx.doi.org/10.1016/0003-4916(74)90208-5
Serot, B.D. and Walecka, J.D. (1986) Advances in Nuclear Physics, 16, 1. Gmuca, S. (1991) Relativistic Mean-Field Fit to Microscopic Results in Nuclear Matter. Journal of Physics G, 17, 1115.
http://dx.doi.org/10.1088/0954-3899/17/7/010 - 10. Gambhir, Y.K. and Ring, P. (1988) Relativistic Description of Deformed Rare Earth Nuclei. Physics Letters B, 202, 5-9.
http://dx.doi.org/10.1016/0370-2693(88)90843-X - 11. Mishra, A., Mishra, H. and Misra, S.P. (1990) Nuclear Matter with Constituent Meson Quanta. International Journal of Modern Physics A, 5, 3391-3399.
http://dx.doi.org/10.1142/S0217751X90001483 - 12. Eisenberg, J.M. (1981) A Heuristic Model for Nucleon Effective Mass Features in the Presence of Pion Condensation. Physics Letters B, 104, 353-356.
http://dx.doi.org/10.1016/0370-2693(81)90696-1
Jung, H., Beck, F. and Miller, G.A. (1989) Relativistic Pion-Ring Series for Nuclear Matter. Physical Review Letters, 62, 2357-2360.
http://dx.doi.org/10.1103/PhysRevLett.62.2357 - 13. Mishra, H., Misra, S.P., Panda, P.K. and Parida, B.K. (1992) Hot Nuclear Matter: A Variational Approach. International Journal of Modern Physics E, 1, 405-419.
http://dx.doi.org/10.1142/S0218301392000229 - 14. Umezawa, H., Matsumoto, H. and Tachiki, M. (1982) Thermo Field Dynamics and Condensed States. North Holand, Amsterdam.
- 15. Sarangi, S., Panda, P.K., Sahu, S.K. and Maharana, L. (2008) Asymmetric Nuclear Matter: A Variational Approach. International Journal of Modern Physics B, 22, 4524-4537.
http://dx.doi.org/10.1142/S0217979208050279 - 16. Sarangi, S., Panda, P.K., Sahu, S.K. and Maharana, L. (2010) Study of the Asymmetric Nuclear Matter with Pion Dressing. Indian Journal of Physics, 84, 431-447.
http://dx.doi.org/10.1007/s12648-010-0028-9 - 17. Sahu, S.K. (2015) Low Density Instability in Asymmetric Nuclear Matter Using Pion Dressing. Journal of Modern Physics, 6, 1350-1359.
http://dx.doi.org/10.4236/jmp.2015.69140 - 18. Fetter, A.L. and Walecka, J.D. (1971) Quantum Theory of Many Particle System. McGraw-Hill Book Company, New York, 34.
- 19. Steiner, A.W., Prakash, M., Lattimer, J.M. and Ellis, P.J. (2005) Isospin Asymmetry in Nuclei and Neutron Stars. Physics Reports, 441, 325-375.
http://dx.doi.org/10.1016/j.physrep.2005.02.004 - 20. Santos, A.M., Providecia, C. and Panda, P.K. (2009) Low Density Instabilities in Asymmetric Nuclear Matter within the Quark-Meson Coupling (QMC) Model with the δ Meson. Physical Review C, 79, Article ID: 045805.
http://dx.doi.org/10.1103/PhysRevC.79.045805













