Journal of Applied Mathematics and Physics
Vol.03 No.09(2015), Article ID:59718,7 pages
10.4236/jamp.2015.39142
Generalization of the Global Error Minimization for Constructing Analytical Solutions to Nonlinear Evolution Equations
Serge Bruno Yamgoué, Bonaventure Nana
Department of Physics, Higher Teacher Training College-Bambili, The University of Bamenda, Bamenda, Cameroon
Email: sergebruno@yahoo.fr, na1bo@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 August 2015; accepted 15 September 2015; published 18 September 2015
ABSTRACT
The global error minimization is a variational method for obtaining approximate analytical solutions to nonlinear oscillator equations which works as follows. Given an ordinary differential equation, a trial solution containing unknowns is selected. The method then converts the problem to an equivalent minimization problem by averaging the squared residual of the differential equation for the selected trial solution. Clearly, the method fails if the integral which defines the average is undefined or infinite for the selected trial. This is precisely the case for such non-periodic solutions as heteroclinic (front or kink) and some homoclinic (dark-solitons) solutions. Based on the fact that these types of solutions have vanishing velocity at infinity, we propose to remedy to this shortcoming of the method by averaging the product of the residual and the derivative of the trial solution. In this way, the method can apply for the approximation of all relevant type of solutions of nonlinear evolution equations. The approach is simple, straightforward and accurate as its original formulation. Its effectiveness is demonstrated using a Helmholtz-Duffing oscillator.
Keywords:
Global Error, Minimization, Heteroclinic Solution, Homoclinic Solution, Front/Kink, Dark/Anti-Dark Soliton

1. Introduction
In the last four decades or so, a great deal of scientific research work has been devoted to constructing analytical solutions to nonlinear evolution equations (NEEs) which model problems encounter in the fields of applied mathematics, physics and engineering sciences. Among these NEEs, ordinary differential equations (ODEs) deserve a special attention. In effect, techniques originally developed for solving ODEs are usually applicable to many other types of NEEs by means of appropriate transformations. For instance, partial differential equations (PDE) are commonly turned into ODEs by using the uniform traveling wave transformation [1] . A variant of it, called fractional complex transformation [2] has recently been introduced and enables to transform fractional ODEs into ordinary (i.e., non-fractional) ones. Solving ODEs is therefore an important step for solving NEEs in general.
The solutions of a given ODE can be divided into two groups. The first group comprises unbounded solutions which are of little interest from the viewpoint of applications. The second group is formed of all bounded solutions. It may be further divided into three classes: constant solutions also called fixed points or equilibrium points, periodic (including quasi-periodic) solutions, and bounded non-periodic solutions. Constant solutions are usually considered as trivial solutions and are less interesting than the other two classes of solutions. The bounded non-periodic solutions are constituted mainly of heteroclinic and homoclinic solutions. They are solutions with the specific property of being backward and forward asymptotic to two distinct or the same fixed points (see (4), (5) and (6) below), respectively. In the case of ODEs resulting from wave equations through the uniform travelling wave transformation, they are called soliton and are the most important for the corresponding field of applications.
While exact and closed-form analytical expressions for the solutions of interest are the eventual targets of the continuing research work, it has long been recognized that such solutions are in general impossible, or at best very difficult to obtain. Thus, the efforts dedicated to constructing analytical solutions to nonlinear ODEs are dominated by the development of approximate methods, that is, methods leading to approximate analytical solutions. Numerous approximate analytical techniques are now available in the literature as the results of these efforts. They include: the Newton harmonic balance [3] -[8] , the linear-delta expansion [9] , the Homotopy analysis method [10] , the method of cubication [11] -[13] , the rational harmonic balance method [14] , the global error minimization [15] , the recent method of quintication [16] , to name just a few. Although some of these techniques are very competitive with respect to accuracy, rate of convergence and ease of use, there is always a room for some improvements.
We observe for instance that in the expositions as well as the subsequent applications of all the techniques mentioned above, only periodic motions and their periods are concerned. In fact, a search through the relevant literature indicates, to the best of our knowledge, that most of the approximate methods published so far are designed to deal only with periodic solutions. Non-periodic solutions such as heteroclinic or homoclinic solutions are largely neglected in spite of their well-recognized importance for wave propagation. The development of methods that are also applicable to these types of solutions is undoubtedly desirable. This is our purpose in this paper where this task is tackled through the generalization of an existing method, namely the global error minimization.
The organization of this paper is as follows. In the next section, we revisit the global error minimization method and generalize so as to make it applicable both to periodic and bounded non-periodic solutions. In Section 3, we illustrate the proposed generalization by applying it to the determination of non-periodic solutions of an ODE. We end with our conclusions in Section 4.
2. Revisiting the Global Error Minimization
In this section, the global error minimization [15] for constructing analytical solutions to ODEs is briefly revisited. For the sake of clarity of the presentation, we consider a general second order ODE of the
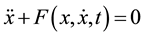 (1)
(1)
which governs the time (t) evolution of the state (x) of a conservative single degree-of-freedom system. Here, an overdot denotes differentiation with respect to time t. Thus, 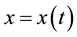 is a real scalar function. In general, (1) is supplemented with initial conditions of the form
is a real scalar function. In general, (1) is supplemented with initial conditions of the form
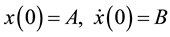 (2)
(2)
where A, B are real constants. Depending on the combination values of these constants and on the function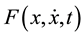 , the solutions of (1) may be periodic, heteroclinic or homoclinic. It was put forth in [15] that excellent approximations to periodic solutions of (1) with (2) can be obtained as functions satisfying (2) which minimize the functional
, the solutions of (1) may be periodic, heteroclinic or homoclinic. It was put forth in [15] that excellent approximations to periodic solutions of (1) with (2) can be obtained as functions satisfying (2) which minimize the functional
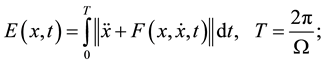 (3)
(3)
where 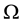 is the unknown angular pulsation of the approximated periodic solution and the “norm” here is defined by
is the unknown angular pulsation of the approximated periodic solution and the “norm” here is defined by . This is the principle of the global error minimization. See [15] for the details.
. This is the principle of the global error minimization. See [15] for the details.
For bounded non-periodic motions, the integration range in (3) should obviously be modified to cover the whole real domain, i.e., it should span from 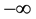 to
to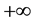 . Now, as pointed out in the introduction, heteroclinic or homoclinic orbits are backward and forward asymptotic to fixed points. In other words, they verify the boundary conditions
. Now, as pointed out in the introduction, heteroclinic or homoclinic orbits are backward and forward asymptotic to fixed points. In other words, they verify the boundary conditions
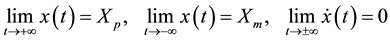 (4)
(4)
with
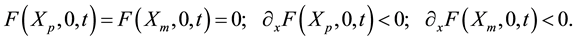 (5)
(5)
The symbol  means partial derivative with respect to x, the first argument of F. Equation (5) is the simplest case of non-degenerate fixed points. It may be replaced for a degenerate fixed point
means partial derivative with respect to x, the first argument of F. Equation (5) is the simplest case of non-degenerate fixed points. It may be replaced for a degenerate fixed point 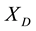 by
by
 (6)
(6)
for some positive integer n. If either of 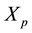 or
or  is different from zero, which is the case for all heteroclinic orbits (characterized by
is different from zero, which is the case for all heteroclinic orbits (characterized by



In this new formulation where the integrand is essentially the product of the original integrand by the velocity, one has to use 



where 



which is a constant of motion. However, since it is not the energy itself which is minimized but its time derivative, the present method is different from energy minimization methods available in the literature [17] [18] .
An important point in methods of minimization is the determination of the trial function. The quality of the approximation depends crucially on how good the trial solution captures the properties of the exact solution. For periodic solutions of angular pulsation

For conservative autonomous problems, it has been shown that the magnitude 

monic decreases exponentially as k increases. If the problem additionally possesses the odd-parity property, then its solutions contain only odd harmonics [19] . The information enables to construct good approximations to the periodic solutions by truncating the expansion in (10) to some finite order and eventually retaining only the appropriate harmonics.
Contrarily to the case of periodic solutions, little is known on how to construct good approximate trial for non-periodic solutions. Here we propose the following ansatze [20]

and

for solutions of the homoclinic type or heteroclinic type, respectively. In principle, all of the fixed points 








Each of the summations in (11) and (12) must obviously be truncated conveniently to keep the analysis manageable, as it is the case when one deals with periodic solutions. Very often, the nonlinear function F in (1) is polynomial. In this case, we suggest the principle of homogeneous balance [20] as a first hand rule for determining the truncation orders, i.e. the highest degrees




est degree of nonlinearity balance each other.
3. Illustrative Example
This section is devoted to the illustration of the revisited formulation of the global error minimization presented above. Our focus is the approximation of homoclinic and heteroclinic orbits for which the classical formulation of the method cannot apply. The model problem chosen for this purpose is described by the Helmholtz-Duffing equation given by

This is an autonomous conservative system for which the restoring force function is the gradient of the potential

When the two coefficients 


equilibrium points including the trivial stable one

and

The point 



We now embark on approximating the homoclinic orbits identified above using the generalized formulation of the global error minimization proposed in this paper. We shall restrict ourselves to solutions which contain only the sech function. By applying the principle of homogeneous balance, we determine the truncation order to be

with

The sole unknown here is



The coefficients of the polynomial Equation (18) are given by:



Figure 1. Profiles of the potential ((a) and (c)) and the corresponding homoclinic orbits ((b) and (d)) for Equation (13). ?α2 < 4β < 0 for (a)-(b) and 0 < β for (c)-(d).


Equations (18)-(19) can be solved exactly analytically. But, it is more convenient to analyze them using numerical simulations.
First, we choose

and

are the value which approximate, respectively, the right and left homoclinic orbits of Figure 1(b). Next, we take


approximates the homoclinic solution of Figure 1(d). We provide a comparison between these approximate solutions to the exact ones in Figure 2. The latter are obtained numerically by using the ode45 function of the Matlab software. One can observe that the accuracy is very satisfactory in spite of the low order of the approximation.
4. Discussion and Conclusions
In this paper, we have proposed a generalization of the method of global error minimization for solving nonlinear ODEs. It consists of establishing the nonlinear algebraic equations verified by the parameters of an ansatz, intended to approximate the solution of a given ODE, by minimizing the averaged product of the derivative of the ansatz with the residual of the ODE for this ansatz. The proposed generalization targets specifically heteroclinic and non-vanishing tails homoclinic solutions for which the original formulation of the method could not apply. The non-suitability of the original formulation is due to the fact that the residual alone is generally not square integrable for arbitrary trial solutions. This is also true for other variational methods, including Hamiltonian and Lagrangian techniques; although the case of homoclinic solutions can be managed by translating the origin to the fixed
An example has been given to illustrate the effectiveness of the approach. For two different sets of parameters values, we have observed that it yields satisfactory results with, however, varying degree of accuracy; as for all
Figure 2. Comparison of approximate analytical solutions (magenta color) to exact numerical ones (blue color) for the Helmholtz-Duffing Equation (13) for


approximate methods. Being a variational method, the quality of the results will depend on how good the trial solutions fit the exact ones. We have proposed some general formulae in terms of hyperbolic tangent and secant for constructing such trial solutions for the two specific types of solutions which have been the focus of this work. However other forms, including exponential, algebraic, rational or gaussian can equally be used.
We have concentrated on the case of a scalar variable in our presentation in this paper. But the method can easily be applied to the case of system of coupled ODEs. For, it suffices to consider




Cite this paper
Serge BrunoYamgoué,BonaventureNana, (2015) Generalization of the Global Error Minimization for Constructing Analytical Solutions to Nonlinear Evolution Equations. Journal of Applied Mathematics and Physics,03,1151-1158. doi: 10.4236/jamp.2015.39142
References
- 1. Griffiths, G.W. and Schiesser, W.E. (2012) Traveling Wave Analysis of Partial Differential Equations: Numerical and Analytical Methods with Matlab and Maple. Academic Press, New York.
- 2. Li, Z.B. and He, J.H. (2010) Fractional Complex Transformation for Fractional Differential Equations. Computer and Mathematics with Applications, 15, 970-973.
- 3. Wu, B.S. and Li, P.S. (2001) A Method for Obtaining Approximate Analytical Periods for a Class of Nonlinear Oscillators. Meccanica, 36, 167-176.
http://dx.doi.org/10.1023/A:1013067311749 - 4. Wu, B.S. and Lim, C.W. (2004) Large Amplitude Non-Linear Oscillations of a General Conservative System. International Journal of Non-Linear Mechanics, 39, 859-870.
http://dx.doi.org/10.1016/S0020-7462(03)00071-4 - 5. Wu, B.S., Sun, W.P. and Lim, C.W. (2006) An Analytical Technique for a Class of Strongly Non-Linear Oscillators. International Journal of Non-Linear Mechanics, 41, 766-774.
http://dx.doi.org/10.1016/j.ijnonlinmec.2006.01.006 - 6. Yamgoué, S.B. and Kofané, T.C. (2008) Linearized Harmonic Balance Based Derivation of the Slow Flow for Some Class of Autonomous Single Degree of Freedom Oscillators. International Journal of Non-Linear Mechanics, 43, 993-999.
http://dx.doi.org/10.1016/j.ijnonlinmec.2008.05.001 - 7. Yamgoué, S.B. (2012) On the Harmonic Balance with Linearization for Asymmetric Single Degree of Freedom Non-Linear Oscillators. Nonlinear Dynamics, 69, 1051-1062.
http://dx.doi.org/10.1007/s11071-012-0326-1 - 8. Yamgoué, S.B., Nana, B. and Lekeufack, O.T. (2015) Improvement of Harmonic Balance Using Jacobian Elliptic Functions. Journal of Applied Mathematics and Physics, 3, 680-690.
http://dx.doi.org/10.4236/jamp.2015.36081 - 9. Amore, P. and Aranda, A. (2003) Presenting a New Method for the Solution of Nonlinear Problems. Physics Letters A, 316, 218-225.
http://dx.doi.org/10.1016/j.physleta.2003.08.001 - 10. Liao, S.J. (2003) Beyond Perturbation: Introduction to Homotopy Analysis Method. Chapman & Hall/CRC Press, Boca Raton.
http://dx.doi.org/10.1201/9780203491164 - 11. Yuste Bravo, S. (1991) Comments on the Method of Harmonic Balance in Which Jacobian Elliptic Functions Are Used. Journal of Sound Vibration, 145, 381-390.
http://dx.doi.org/10.1016/0022-460X(91)90109-W - 12. Yuste Bravo, S. (1992) “Cubication” of Non-Linear Oscillators Using the Principle of Harmonic Balance. International Journal of Non-Linear Mechanics, 27, 347-356.
http://dx.doi.org/10.1016/0020-7462(92)90004-Q - 13. Beléndez, A., Méndez, D.I., Fernandez, E., Marini, S. and Pascual, I. (2009) An Approximate Solution to the Duffing-Harmonic Oscillator by a Cubication Method. Physics Letters A, 373, 2805-2809.
http://dx.doi.org/10.1016/j.physleta.2009.05.074 - 14. Yamgoué, S.B., Bogning, J.R., Kenfack Jiotsa, A. and Kofané, T.C. (2010) Rational Harmonic Balance-Based Approximate Solutions to Nonlinear Single-Degree-of-Freedom Oscillator Equations. Physica Scripta, 81, Article ID: 035003.
http://dx.doi.org/10.1088/0031-8949/81/03/035003 - 15. Farzaneh, Y. and Tootoonchi, A.A. (2010) Global Error Minimization Method for Solving Strongly Nonlinear Oscillator Differential Equations. Computers and Mathematics with Applications, 59, 2887-2895.
http://dx.doi.org/10.1016/j.camwa.2010.02.006 - 16. Elias-Zuniga, A. (2014) “Quintication” Method to Obtain Approximate Analytical Solutions of Non-Linear Oscillators. Applied Mathematics and Computations, 243, 849-855.
http://dx.doi.org/10.1016/j.amc.2014.05.085 - 17. He, J.H. (2002) Preliminary Report on the Energy Balance for Nonlinear Oscillators. Mechanics Research Communications, 29, 107-111.
http://dx.doi.org/10.1016/S0093-6413(02)00237-9 - 18. He, J.H. (2010) Hamiltonian Approach to Nonlinear Oscillators. Physics Letters A, 374, 2312-2314.
http://dx.doi.org/10.1016/j.physleta.2010.03.064 - 19. Mickens, R.E. (2002) Fourier Representations for Periodic Solutions of Odd-Parity Systems. Journal of Sound and Vibration, 258, 398-401.
http://dx.doi.org/10.1006/jsvi.2002.5200 - 20. Baldwin, D., Göktas, ü., Hereman, W., Hong, L. Martino, R.S. and Miller, J.C. (2004) Symbolic Computation of Exact Solutions Expressible in Hyperbolic and Elliptic Functions for Nonlinear PDEs. Journal of Symbolic Computations, 37, 669-705.
http://dx.doi.org/10.1016/j.jsc.2003.09.004



