Received 21 May 2015; accepted 27 June 2015; published 30 June 2015

ABSTRACT

In this paper, we propose and analyze a non-monotone trust region method with non-monotone line search strategy for unconstrained optimization problems. Unlike the traditional non-mono- tone trust region method, our algorithm utilizes non-monotone Wolfe line search to get the next point if a trial step is not adopted. Thus, it can reduce the number of solving sub-problems. Theo- retical analysis shows that the new proposed method has a global convergence under some mild conditions.

Keywords:

Unconstrained Optimization, Non-Monotone Trust Region Method, Non-Monotone Line Search, Global Convergence

1. Introduction

Consider the following unconstrained optimization problem:

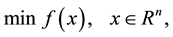(1)

where is a twice continuously differentiable function. Throughout this paper, we use the following notation:

・ is the Euclidean norm.

・ and 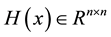are the gradient and Hessian matrix of f evaluated at x, respectively.

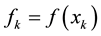・ , , and 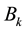is a symmetric matrix which is either 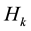or an approximation of.

For solving (1), trust region methods usually compute 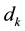by solving the quadratic sub-problem:

(2)

where is a trust region radius. Some criteria are used to determine whether a trial step is accepted. If not, the sub-problem (2) may be computed several times at one iterate until an acceptable step is found. There is no doubt that the repetitive process will increase the cost of solving the problem.

To improve the performance of the algorithm, Nocedal and Yuan [1] put forward an algorithm which combine trust region algorithm and line search method for the first time in 1998, then Gertz [2] proposed a new trust region algorithm that use Wolfe line search at each iteration to obtain a new iteration point regardless of whether 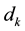is accepted. Both of them improved the computational efficiency by fully using the advantages of two kinds of algorithm.

Algorithms mentioned above are monotonic algorithm. In 1982, Chamberlain et al. in [3] proposed the watchdog technique for constrained optimization to overcome the Maratos effect. Motivated by this idea, Grippo et al. first introduced a non-monotone line search technique for Newton’s method in [4] . In 1993, Deng et al. [5] proposed a non-monotone trust region algorithm in which they combined non-monotone term and trust region method for the first time. Due to the high efficiency of non-monotone techniques, many authors are interested in working on the non-monotone techniques for unconstrained optimization problem [6] - [15] . Especially, some researchers have combined non-monotone trust region method with non-monotone Armijo-type line search method and good numerical results have been achieved [16] [17] . Besides, Zhang and Hager [18] proposed a non-monotone Wolfe-type condition. Inspired by [16] - [18] , we present a non-monotone trust region algorithm with non-monotone Wolfe-type line search strategy. To be specific, the algorithm first solve sub-problem (2) to compute the trial step, if the trial step is accepted, set. Otherwise, the algorithm performs the non-monotone Wolfe-type line search strategy to find an iterative point instead of resolving the sub-prob- lem.

2. Non-Monotone Term and Wolfe-Type Line Search Condition

The general non-monotone form is as follows:

(3)

where, and is an integer constant. Actually, the most common non-monotone ratio is defined as follows:

.

Some researchers showed that utilizing non-monotone techniques may improve both the possibility of finding the global optimum and the rate of convergence [4] [18] . However, although the non-monotone technique has many advantages, it contains some drawbacks [11] [17] [18] . To overcome those disadvantages, Ahookhosh et al. in [11] proposed a new non-monotone technique to replace (3). They define

(4)

where, and. At the same time, they have the new non-monotone ratio:

(5)

In 2004, Zhang and Hager [18] presented a modified non-monotone Wolfe-type condition. In order to keep the consistency of non-monotone term and simplify the form of Wolfe-type condition, we define the new modified non-monotone Wolfe-type condition as follows:

(6)

(7)

The rest of this paper is organized as follows. In Section 3, we introduce the algorithm of non-monotone trust region method with line search strategy. In Section 4, we analyze the new method and prove the global convergence. Some conclusions are given in Section 5.

3. New Algorithm

In this paper, we consider the following assumptions that will be used to analyze the convergence properties of the below algorithm:

(H1) The level set, where is a closed, bounded set.

(H2) The matrix is a uniformly bounded matrix, i.e. there exists a constant such that for all k.

(H3) is a Lipschitz continuous function, i.e. there exists a constant such that .

(H4) has the upper bound.

The new algorithm can be described as follows:

Algorithm 0

Step 1 An initial point and a symmetric positive definite matrix are given. The constants, , , , , , and are also given. Compute and set.

Step 2 Compute. If then stop, else go to Step 3.

Step 3 Similar to [1] , solve (2) inaccurately to determine, satisfying

(8)

(9)

Step 4 Compute, , and. If, go to Step 5. Otherwise, find the step-length satisfying (6) and (7), then set and update, go to step 6.

Step 5 Set, and

.

Step 6 Update the symmetric matrix by a quasi-Newton formula, set, go to step 2.

4. Convergence Analysis

For the convenience of expression, we Let and. Obviously, is an infinite subset of the set.

We need the following lemmas in order to prove the convergence of the new algorithm.

Lemma 1 Assume that Algorithm 0 generates an infinite sequence, (H2), (H3) and (H4) hold, and there is a such that. Then for all, there exists a constant such that.

Proof. From (7) and (H3), we have

. (10)

Thus, we can conclude that

. (11)

This inequality, together with (H2), (H4) and (9), lead us to have

. (12)

Let, we complete the proof.

Lemma 2 (See Lemma 2.1 and Corollary 3.1 in [17] ) Suppose that the sequence is generated by Algorithm 0. Then, we have, is a decreasing sequence and

(13)

Lemma 3 Suppose that (H1) holds, if sequence does not converge to a stationary point, i.e. there exists a constant such that. Then

(14)

where

Proof. We consider two cases:

Case 1.. The proof is similar to Lemma 3.3 in [17] , we can obtain that

.

Case 2.. From (6), (9) and (12), we have

where.

Let, we can conclude

. (15)

Considering Lemma 2 and (15), we get (14).

Lemma 4 Suppose that all conditions of Lemmma 1 and Lemma 3 hold. Then for all sufficiently large k, we have

. (16)

Proof. The proof is similar to Lemma 3.6 and 3.7 in [16] , we omit it for convenience.

Lemma 5 Suppose that (H2) and (H3) hold, if there exists a constant such that, then for a sufficiently large integer, we have.

Proof. Assume that for, (16) holds. Using the fact and (15), we obtain

.

Then, the monotonicity of imply that

Thus, for we have

Using Lemma 2, we get

.

This inequality and the fact that is convergent (see [4] ) show

.

Therefore,. Then we have.

Theorem 6 Suppose that (H1)-(H4) hold, then sequence generated by Algorithm 0 satisfies

. (17)

Proof. Assume that (17) does not hold, then there exists a constant such that. From (H2) and the definition of, we have

.

Obviously, this contradicts Lemma 5. The proof is completed.

5. Conclusion

In this paper, we introduce the algorithm of non-monotone trust region method with non-monotone Wolfe-type line search strategy for unconstrained optimization problems based on (5), (6) and (7). When compared with (3), it is obviously that we fully employ the current objective function value and we can derive the better convergence results by choosing an adaptive. Besides, with the help of line search strategy, new algorithm can reduce the number of solving sub-problems. We analyzed the properties of the algorithm and proved the global convergence theory under some mild conditions.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (61473111) and the Natural Science Foundation of Hebei Province (Grant No. A2014201003, A2014201100).

References

NOTES

^*Corresponding authors.