Journal of Applied Mathematics and Physics Vol.02 No.13(2014),
Article ID:52523,16 pages
10.4236/jamp.2014.213142
Regression-Tensor Modeling of Multivariate Optimization of Process for Applying Metal Coatings
Vyacheslav Anatolievich Rusanov1, Sergey Viktorovich Agafonov2, Sergey Nikolayevich Dumnov3, Aleksey Vasilyevich Daneev3, Sergey Vasilyevich Lyamin3
1Institute for System Dynamics and Control Theory of Siberian Branch of Russian Academy of Sciences (ISDCT SB RAS), Irkutsk, Russia
2Irkutsk State Agricultural Academy (ISAA), Irkutsk, Russia
3Irkutsk State Transport University (ISTU), Irkutsk, Russia
Email: v.rusanov@mail.ru, daneev@mail.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 October 2014; revised 7 November 2014; accepted 21 November 2014
ABSTRACT
A universal regression-tensor approach is developed in the mathematical modeling of optimal parameters of chemical-technological process of complex mechanical products. The testing of developed algorithms was performed on the example of multi-factorial process of low-temperature sulfur-chromium plating of precision mechanical parts.
Keywords:
Covariant Tensors of Final Valence, Identification of Nonlinear Vector Regression, Optimization of Metal Coatings

1. Introduction
Originally regression analysis acquired theoretical and applied interest in problems of optimizing the parameters of linear stationary systems (type “black box”). In most cases, the studies were limited with analysis of finite- dimensional systems [1] [2] ; as a rule, the problem of identification of regression was formulated in terms of computing quadratic-optimal estimation of model parameters using the method of least squares with following application of constructing pseudo-inverse matrix ( [3] p. 186).
In this article regression analysis differs from the traditional presentation [1] [2] because one of the main goals was to present more clearly geometrical (in the language of constructions [4] [5] ) device of multivariate nonlinear regression modeling [6] (with simultaneous reduction of dimension of used pseudo-matrix). According to this applied interpretation of theoretical results of the article [6] is studied in details below; it is interesting in connection with other applications of method of least squares-interpolation where generalizations of algorithmic solutions proposed in [6] can manifest.
The approbation of theoretical apparatus of nonlinear vector regression in the article stands the problem of optimization (as a way of technological calculation) of characteristics of multi-factorial chemical-technological process. Payment of optimization of process of low-temperature sulfur-chromium plating of precised mechanical products is taken as example.
2. The Statement of the Problem of Modeling of Optimal Chemical-Technological Process
Let R-field of real numbers,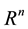 ―n-dimensional vector space over R with Euclidian norm
―n-dimensional vector space over R with Euclidian norm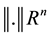 ,
,
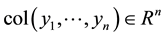 ―column vector
with elements
―column vector
with elements
 and let
and let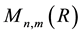 ―space
of all n ´ m-ma- trices with elements from R and Frobenius matrix norm
―space
of all n ´ m-ma- trices with elements from R and Frobenius matrix norm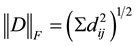 ,
,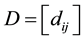 . Further through
. Further through
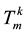 we denote the space of all covariant tensors k-th valence (real multi-linear forms
we denote the space of all covariant tensors k-th valence (real multi-linear forms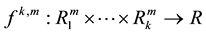 ) with tensor
norm
) with tensor
norm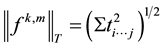 , where
, where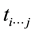 ―coefficients
( [4] p. 61) of a tensor
―coefficients
( [4] p. 61) of a tensor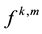 ,
the values of which are
,
the values of which are
relative to the standard algebraic basis ( [7] p. 15) in the Euclidean space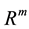 .
.
Let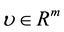 ―vector
of varied physicochemical predictors ( [2] p. 38) of regression of chemical-technological
―vector
of varied physicochemical predictors ( [2] p. 38) of regression of chemical-technological
process with fixed origin in
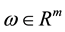 (reference mode), w
(reference mode), w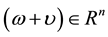 ―vector
of qualitative indexes of
―vector
of qualitative indexes of
chemical-technological process. In this setting we select for consideration a nonlinear system of type “input-output” described by vector-tensor k-valent equation of multiple regression

where






The statement of the problem of optimization of chemical-technological process consists of three steps:
(i) for a fixed index k given





(ii) to build a posteriori estimates c, A,



parametric regression model (1):

here


with respect to “point” of reference mode of chemical-technological process
(iii) for




where
and variables of vector-function

3. Existence of a Model of Multivariate Regression of Chemical-Technological Process
In this section we will examine the analytic properties of nonlinear vector regressions of many variables that look like behavior of holomorphic functions (problem (i) from paragraph 1). In connection with this the presentation will be based on the concept of the Frechet derivative ( [5] p. 48). Last poses the problem of determining the remaining concepts in particular the higher order differentials through the design of these derivatives; it is known ( [5] p. 490), that Frechet k-derivatives can be (and most comfortable) interpreted as mathematical constructions with multi-linear (k-linear) structure that reflects the following:
Proposition 1. Let W―open area in


Proof. Each derivative




Before we take a further step we note that formulation of Proposition 1 essentially imposes on the map w(×) one additional requirement, namely, position of analytical representation of vector-function w(×). In the case of a posteriori modeling w(×) this requirement is not feasible, so above we are limited with the analysis according to the problem (i) less realistic, but more logically verified task of analysis of the properties of mapping w(×).
In next assertion we establish an important property which a vector-function w(×) should have clarifying: when the mapping w(×) satisfies at least under some reasonable assumptions on it one of those special laws from which a concept of tensor regression (1) happened as a natural product of a continuous process of consolidation, abstraction and generalization.
Proposition 2. Let W―open domain in








Proof. By theorem 2 ( [5] p. 491) uniform continuity of the strong derivative w(k)(×)
of mapping


where vector-function e(w,×) of class

Thus, the compilation of this proposal with Formula (4) leads to
where


Remark 1. Everywhere further we believe a priori that the simulated chemical-technological process satisfies the Proposition 2 for some index k ³ 2.
The Proposition 2 provides the most direct way of interpreting the concept of model
complexity because it shows a direct link between the approximate model and the
way the model should be evaluated from experimental data which in the strict sense
refuse it; when we set the maximum allowable inconsistency

4. Identification of Quadratic-Vector Regression Model of Chemical-Technological Process
Let’s start with specification of tensor construction of Equation (1); this specification
has a special character but its use in potential allows not to attract complex computational
algorithms for calculating an optimal vector of variables of chemical-technological
process. We consider (including Remark 1) the case k = 2. We also agree that the
coordinates





where

By Proposition 2 and Theorem 12 ( [8] p. 189) we have an obvious interpretations:
here

We will associate methodologically the parametric identification in multi-criteria vector-matrix-tensor formulation (2) for multiple stationary nonlinear model of type “black box” in class of regressions (5) with the concept of normal pseudo-solution for a finite-dimensional system of linear algebraic equations.
As usual ( [7] p. 501) normal pseudo-solution of system of algebraic equations







note the generalized inverse (pseudo-inverse) matrix of Moore-Penrose ( [7] p. 500) of matrix D; asymptotic construction of pseudo-inverse matrix has the following analytical form of
Then (see Formula (50), [8] p. 35) vector

We assume that during the operation of chemical-technological process there were
conducted q-experiments of type “input-output”. For parameters of quadratic regression
system (5) and q-data (general sample) of conducted experiments we denote through




We call complete matrix of experimental data of input variables of chemical-technological process (6) q ´ m(m + 3)/2-matrix of type
respectively vector
we will call the complete vector of experimental data of i-th output variable.
Further considering that in system (5) each matrix Bi is upper triangular
the structure of i-th equation


It is clear that in view of algebraic structure of Equation (7) the problem of parametric
identification (2) should be solved on some basis of q-experiments with respect
to the next group of vectors (of dimension

it is obvious that this group of vectors completely determines (sets) elements of
matrix



Now we can give the solution to the problem of parametric identification of model of bilinear-tensor regression of chemical-technological process only by a posteriori information on the basis of preliminary passage of q- experiments.
Proposition 3. The problem of identification (2) in terms of parameters (8) of regression model (5) has a solution:
where U―full matrix of experimental data of input actions (6),

Proof. Below we will give a sketch of the proof. Following the standard arguments regression (5) for each l-th experiment according to the relations (6), (7) takes the following compact form:
Thus, if we reformulate according to the last system, optimization problem of parametric
identification (2) applied to the equations of regression in tensor structure (5),
then we arrive to the following multi-criteria formulation with respect to vectors
It is not difficult to establish that this multi-criteria formulation has (according
to Formula (50), [9] p. 35) only one normal pseudo-solution


Corollary 1 ( [10] p. 263). Let

sion model (5) which characterizes the behavior of chemical-technological process
such that

(*)
(**)

Remark 2. Ratings (*), (**) primarily depend on the “volume” of a posteriori information
in the formation of matrix U and vectors


5. Optimization of the Mode of Chemical-Technological Process Based on Quadratic Interpolation of Its Functional Model
An attractive idea to create engineering projects and algorithms that are adapted
to changing conditions of studied (in the frameworks of these projects) chemical-technological
processes, requires the use of nonlinear regression models of class (5) which are
optimal flexible (tunable) during the variety of experimental data. Therefore the
parametric identification of the functional model of chemical-technological process
of class of regressions (5) studied in the previous section was necessary “technological”
requirement in solving the problem of “synthesis control”


Proposition 4. Let



may have an inner extremum (at

where

-if

-if

-if

Remark 3. In the first two cases of definite sign of quadratic form

Proof of Proposition 4. Since
then the necessary conditions of a local extremum have ( [5] p. 500) the form:
that is equivalent to the system of equations (below

which (as it has been easily seen) determine in the space


On the other hand, the definite sign of the second differential
determines sufficient conditions ( [5] p. 503) for a local extremum at the critical point (9). □
Coordinates of the stationary point (9) allow us to answer the question about the
meaning of the functional
Corollary 2. If Di―is a negative definite (similarly positive definite)
matrix, then maximum (or minimum) value of the functional

where ci―i-th coordinate of the vector

The proof is constructed by substituting (9) in (1).
Now we will turn to the study of more complex (task (iii)) variant of the problem
of optimization of characteristics of chemical-technological process which plays
the fundamental role in a more realistic and at the same time more difficult problems
in calculating the optimal technological parameters of the mode of functioning of
chemical-technological process. Its basis is the methodological position―each functional

Proposition 4. Let






while a sufficient condition that v* provides the quality for a chemical-technological process
is the following requirement: stationary point v* has an elliptic type which is equivalent to the position:

where

Proof. Main provisions of the proof repeat the conclusion of Proposition 4 that’s why we are restricted by the scheme of the proof. Necessary conditions of a local extremum have ( [5] p. 500) the form of n equations:
which is equivalent to the system of n equations:
the last system leads to the solution (10). □
If algebraic conditions (11) (equivalent to (12)) don’t meet then the critical point (10) of functional quality of chemical-technological process is either ( [7] p. 288) hyperbolic (i.e. saddle point) or parabolic point and therefore it requires additional geometric analysis of critical controlled variables of chemical-technological process expressed by the formula (10).
Speaking more formally we can quote: the presence of a saddle point warrants a change in at least one (but not all) inequality “<” from (11) (or (12)) on inequality “>”; while a similar change of relation “<” on “£” may causes the structure of parabolic point in the analytical solution of the problem of optimization.
The presented approach methodologically extends the standard procedure of planning
experiment of chemical-technological process. Thus, if the calculated (predicted)
coordinates of the stationary point (10) of any che- mical-technological parameters
are outside the area of adequacy of the identified model (5), it is necessary to
conduct an additional experiment while implement chemical-technological process
with vector
6. Numerical Modeling of the Mode of Chemical-Technological Process
The previous sections have been conceived as an attempt to bring “compactly” together under the same terms and notations large but diverse enough number of rigorous mathematical results that are dedicated to such a broad topic as multivariate regression analysis with emphasis on methods of covariant-tensor representation of functional derivatives (Frechet derivatives) involving the method of the least squares and their practical application to the optimization of complex multivariate processes. Next section is devoted to a detailed study of related concepts while the basic attention is focused on experimental testing of the theoretical results from Paragraphs 1 - 4 on the basis of experimental studies of process of low-temperature sulfur-chromium.
Numerical modeling was carried out in the environment of software package [12] which solves practical issues of regression-tensor modeling of multivariate chemical-technological process. Rigorous analytical interpretations of multiple technical constraints are determined on its base, imposing as complex nonlinear constraints both theoretical and empirical character and ensuring the adequacy of investigated model by a posteriori data―the problem of identification by the method of the least squares of coordinates of covariant tensors (both linear and bilinear) of multidimensional nonlinear regression. At the final step this modeling “connects” algorithms of quadratic optimization of synthesis of optimal technological characteristics of behavior of chemical- technological process.
Without loss of generality as a reference mode of process of low-temperature sulfur-chromium
we can take some point w of space Rm empirically selected from the overall
composition of the experimental data; it is clear that in this case coordinates


Parameters of reference mode: w1 = 125˚C, w2 = 0.92 hour, w3 = 43% NaOH, w4 = 0.5% S, w5 = 1% Na2S, w6 = 2% Na2S2O3, w7 = 10% CrO3.
Multivariate synthesis of sulfur-chromium layer in the series from field experiments q (due to m = 7 and p. (**) of Corollary 1 the number of experiments q £ 35) we will describe with the following chemical-technolo- gical variables:
Input data:








Output data:

The solution of the problem of parametric identification (2) for the regression Equation (5) of process of low- temperature sulfur-chromium presented in Table 1 by Proposition 3 and calculations in the software environment [12] , has the form:

Critical analysis of efficiency of model of the mathematical description of process
of low-temperature sulfur- chromium expressed by Equations (13) gives the comparison
of the last two columns of Table 1; here w1―expe-
riment, ŵ1―forecast according to (13). The graphic illustration of the
index of quality

Figure 1. Dependence of
thickness of sulfur-chromium layer from the temperature and duration of process
of plunger assembly―
Table 1. Process of low-temperature of sulfur-chromium.
Figure 2. Dependence of
thickness of sulfur-chromium layer from concentrations of hydroxide of sodium and
sulfur―
Figure 3. Dependence of
thickness of sulfur-chromium layer from concentrations of sulfur and sulfide of
sodium―
Figure 4. Dependence of
thickness of sulfur-chromium layer from concentrations of sulfide of sodium and
hypsosulfide of sodium―
Figure 5. Dependence of
thickness of sulfur-chromium layer from concentrations of hypophosphite of sodium
and chromium oxide―
Figure 6. Dependence of
thickness of sulfur-chromium layer from concentration of chromium oxide and temperature―
Figure 7. Dependence of
thickness of sulfur-chromium layer from concentrations of chromium oxide and hydroxide
of sodium―
Figure 8. Dependence of
thickness of sulfur-chromium layer from concentrations of chromium oxide and sulfur―
Figure 9. Dependence of
thickness of sulfur-chromium layer from concentrations of chromium oxide and sulfide
of sodium―
7. Optimization of Mode of Chemical-Technological Process
Combining the results of Paragraphs 1 - 4 sulfur-chromium mode providing maximum thickness of physical structure of sulfur-chromium layer of machined surface of precision item we will contact with the solution of the optimization problem of the following form:

Development of new technological methods of processing of metals requires an adequate mathematical model allowing to predict interrelated effect of various factors of physical-chemical environment of the metalworking and mechanical-geometric characteristics of the treated surface of the item on the obtained results. Mathematical model of optimization (14) for a multivariate process of sulfur-chromium gives such an opportunity, namely, to identify the most critical parameters and set determined areas of improvement of used and developed technological plants for obtaining sulfur-chromium layer. Proposition 4 and Formula (9) allowing to calculate geometric coordinates of the stationary point for the problem of optimization determine (in terms of system (13)) the following highly effective technological parameters of the mode of sulfur-chromium: by virtue of system (5) (or that is equivalent to the Equations (13)) a stationary point (9) in the coordinate representation (of a row-vector) has the form:
or the same in the physical dimensions of given “reference” from the mode w:

Mathematical result obtained above (the coordinates of the stationary point of sulfur-chromium
mode (9)) is in accordance with the logic of physical reasoning; illustration

Figure 10. Detail of
the target functional

Figure 11. Detail of
the target functional

Figure 12. Detail of
the target functional

Figure 13. Detail of
the target functional

Figure 14. Detail of
the target functional

Figure 15. Detail of
the target functional

Figure 16. Detail of
the target functional

Figure 17. Detail of
the target functional

Figure 18. Detail of
the target functional

Since own values of the matrix D1 respectively equal

then it speaks about the stationary saddle point of the functional F(v).
According to (12) and (16) in the obtained stationary point v* functional
F(v) reaches its “max” in the variables

The foregoing discussion can be summarized in one sentence: if there is w7 = 9.917% CrO3, then it is necessary to fulfill the conditions
if the position w7 = b ¹ 9.917% CrO is implemented, then it is necessary to decide the correction of the problem (3), (14) of the form in full capacity including the identification (2)
This rule is of course largely engineering (not mathematical); from a purely mathematical
point of view it only specifies the behavior of chemical-technological process stating
that in any case it is necessary to describe (to explain in a heuristic level) the
original choice of the percentage in the solution of three chromium oxide CrO3.
In this connection we will mention another unexpected result: the first six parameters

8. Conclusions
The problem of the analytical description of the a posteriori set of data occurs in many sections of science and technology associated with the modeling and/or identification of cognitive systems. In this context the article discusses theoretical issues of regression-tensor modeling of multivariate chemical-technological process in the class of systems (1) and on its basis rigorous analytical interpretations are given which were imposed as nonlinear constraints of theoretical nature as providing the optimal mode of chemical-technological process.
In Paragraph 2a detailed mathematical study of the question of existence of regression model while particular attention was paid to the role of differential calculation (in the constructions of strong Frechet derivatives) in finite-dimensional Euclidean spaces for receiving qualitative conditions (Proposition 2) in the solution of the task of “satisfactory” modeling. In this regard we will note that the description of chemical-technological process by regression system (1) and differential models [13] is adequate considering assertion ( [5] p. 495) about differential dependence of the solution of differential equation from initial-boundary conditions and parameters as well as Proposition 2.
The problem of identification of the method of least squares of coordinates of covariant tensors of both linear and bilinear is considered in Paragraph 3 of common positions formalized by criterion (2). In the large extent in this part of work the confirmation of algorithmic theory of nonlinear regression-tensor modeling of chemical- technological process in terms of designing rules for calculating parameters (8) by conditions suitable for the application of the optimal estimation (2) of operators of the regression model (1) was received in terms of Proposition 3.
In Paragraph 4 the importance of the theory of a posteriori mathematical modeling of chemical-technological process outlined in previous sections is confirmed by the fact that it is not only analytical (which is important itself) but the fact that it leads to efficient algorithms for synthesis of the optimal chemical-technological process. In this context the formula (9) for calculating geometric coordinates of the stationary point of the optimal mode of chemical-technological process was obtained according to the target criterion (3) as well as sufficient conditions are given to guarantee maximum quality of chemical-technological process in practice.
Paragraphs 5, 6 show the results of the numerical solution based on the experimental data of the problem of identification of bilinear tensors of nonlinear regression model of sulfur-chromium coating layer having the optimal thickness of sulfur-chromium layer. The stages of the numerical solution of the problem of parametric identification were considered while the detected deviations of calculated (predicted) values of synthesized sulfur-chromium layer and experimental data aren’t of fundamental nature in consequence of which effective mathematical method (finite chain of algebraic operations (9)) of calculating the optimal coating thickness providing the parameters of nonlinear multivariate mode of sulfur-chromium space of precision item was investigated and confirmed.
For a more complex chemical-technological process, a broader “dictionary of modeling” and the best knowledge of the theory of multivariate regression-tensor modeling are necessary to describe the structure of the functional (3) and use its properties due to additional research (in the spirit of [14] ) of factors of nonlinearity of models (1):
on identification and algorithmization of procedure of selection of weighted coefficients

on the expansion of the linear-quadratic form of equations of regression (5) of “Taylor decomposition” of vector-function of regression of higher order;
on registration of additional parameters-coordinates of vector-function of regression model such physical- mathematical parameters of chemical-technological process as surface hardness, wear resistance, coefficient of dry friction of treated surface as well as fragility of the resulting metal plating;
on the development of nano-metric indicators of chemical-technological process and their qualitative account in the structure of nonlinear-tensor multidimensional regression model (1).
Acknowledgements
This work was supported by the Program “Leading Scientific Schools” (project no. NSh-5007.2014.09).
References
- Adler, Y.P., Markova, E.V. and Granovsky, Y.V. (1976) Planning of Experiment in Finding the Optimal Conditions. Nauka, Moscow, 255 p. (In Russian)
- Draper, N.R. and Smith, H. (1998) Applied Regression Analysis. John Wiley & Sons Ltd., New York. [(2007) Vilyms, Moscow, 912 p. (In Russian)] http://dx.doi.org/10.1002/9781118625590
- Andrievskiy, B.R. and Fradkov, A.L. (2001) Elements of Mathematical Modeling in Software Environments MAT- LAB and SCILAB. Nauka, Saint-Petersburg, 288 p. (In Russian)
- Akivis, M.A. and Goldberg, V.V. (1972) Tensor Calculation. Nauka, Moscow, 352 p. (In Russian)
- Kolmogorov, A.N. and Fomin, S.V. (1976) Elements of the Theory of Functions and Functional Analysis. Nauka, Moscow, 544 p. (In Russian)
- Rusanov, V.A., Agafonov, S.V., Daneev, A.V. and Lyamin, S.V. (2013) Multivariable Regression Analysis of Optimal Conditions for a Physics-Chemical Process. International Journal of Materials Engineering and Technology, 10, 19-44.
- Horn, P. and Johnson, C. (1989) Matrix Analysis. Mir, Moscow, 656 p. (In Russian)
- Banach, S. (1972) Differential and Integral Calculus. Nauka, Moscow, 424 p. (In Russian)
- Gantmacher, F.R. (1988) Theory of Matrices. Nauka, Moscow, 552 p. (In Russian)
- Lankaster, P. (1982) Theory of Matrices. Nauka, Moscow, 272 p. (In Russian)
- Makarova, I.M., Vinogradskaya, T.M., Rubchinskiy, A.A. and Sokolova, V.B. (1982) Theory of Choice and Decision-Making. Nauka, Moscow, 328 p. (In Russian)
- Agafonov, S.V., Sharpinskiy, D.Y., Rusanov, V.A. and Udilov, T.V. (2008) Hybrid Regression Complex “GREEK”. Certificate of the Federal Service for Intellectual Property, Patents and Trademarks of the Registration of a Computer Program, № 2008614737.
- Kärger, J., Grinberg, F. and Heitjans, P. (2005) Diffusion Fundamentals. Leipziger Univ., Leipzig, 615 p.
- Ross, G.J. (1990) Nonlinear Estimation. Springer-Verlag, New York, 237 p. http://dx.doi.org/10.1007/978-1-4612-3412-8













































