Journal of Applied Mathematics and Physics
Vol.02 No.07(2014), Article ID:46815,5 pages
10.4236/jamp.2014.27064
Steffensen-Type method of super Third-order Convergence for Solving Nonlinear equations
Zhongli Liu*, Hong Zhang
College of Biochemical Engineering, Beijing Union University, Beijing, China
Email: *liuzhongli2@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 March 2014; revised 5 April 2014; accepted 12 April 2014
ABSTRACT
In this paper, a one-step Steffensen-type method with super-cubic convergence for solving nonli- near equations is suggested. The convergence order 3.383 is proved theoretically and demon- strated numerically. This super-cubic convergence is obtained by self-accelerating second-order Steffensen’s method twice with memory, but without any new function evaluations. The proposed method is very efficient and convenient, since it is still a derivative-free two-point method. Its theoretical results and high computational efficiency is confirmed by Numerical examples.
Keywords:
Newton’s Method, Steffensen’s Method, Derivative free, Super-cubic Convergence, Nonlinear Equation

1. Introduction
Finding the root of a nonlinear equation
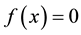 (1)
(1)
is a classical problem. It is well-known in scientific computation that Newton’s method (NM, see [1] ):
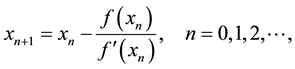 (2)
(2)
is widely used for root-finding, where  is an initial guess of the root. However, when the derivative
is an initial guess of the root. However, when the derivative  is unavailable or is expensive to be obtained, the derivative-free method is necessary. If the derivative
is unavailable or is expensive to be obtained, the derivative-free method is necessary. If the derivative 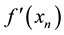 is replaced by the divided difference in (2), Steffensen’s method (SM, see [1] ) is obtained as follows:
is replaced by the divided difference in (2), Steffensen’s method (SM, see [1] ) is obtained as follows:
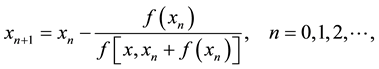 (3)
(3)
NM/SM converges quadratically and requires two function evaluations per iteration. The efficiency index of them is .
.
Besides H.T. Kung and J.F. Traub conjectured that an iterative method based on 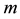 evaluations per iteration without memory would arrive at the optimal convergence of order
evaluations per iteration without memory would arrive at the optimal convergence of order 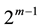 (see [2] ), Traub proposed a self-acce- lerating two-point method of order 2.414 with memory (see [3] ):
(see [2] ), Traub proposed a self-acce- lerating two-point method of order 2.414 with memory (see [3] ):
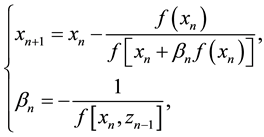 (4)
(4)
where , and
, and  or
or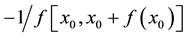 , etc.
, etc.
A lot of self-accelerating Steffensen-type methods were derived in the literature (see [1] - [7] ). Steffensen-type methods and their applications in the solution of nonlinear systems and nonlinear differential equations were discussed in [1] [4] [5] [8] . Recently, by a new self-accelerating technique based on the second-order Newtonian
interpolatory polynomial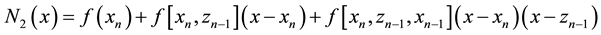 , J. Džunića
, J. Džunića
and M.S. Petkovića proposed a cubically convergent Steffensen-like method (see [7] ):
 (5)
(5)
In this study, a one-step Steffensen-type method is proposed by doubly-self-accelerating in Section 2, its super-cubic convergence is proved in Section 3, and numerical examples are demonstrated in Section 4.
2. The Method of Steffensen-Type
By the first-order Newtonian interpolatory polynomial  and
and

we have
where

So, with some

should be better than 

Therefore, we suggest 

where





vanish the asymptotic convergence constant, we establish a self-accelerating Steffensen’s method with super quadratic convergence as follows:

Furthermore, we propose a one-step Steffensen-type method with super cubic convergence by doubly-self- accelerating as follows:
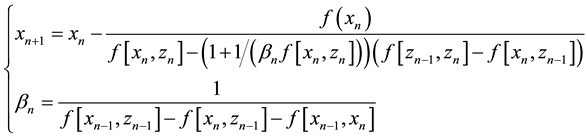
3. Its Super Third-order Convergence
Lemma 3.1 


Proof. By Taylor formula, we have
So,
Then, the proof can be completed.
Theorem 3.2 Let 




Proof. If 


and if 


Then
By Taylor formula and Lemma 3.1, we also have

So, comparing the exponents of 


From its non-trivial solution 

As the efficiency index is
and (9) are 

4. Numerical examples
Related one-step methods only using two function evaluations per iteration are showed in the following numeri- cal examples. The proposed method is a derivative-free two-point method with high computational efficiency.
Example 1. The numerical results of NM, SM, (4), (5) and (9) in Table 1 agree with the theoretical analysis. The computational order of convergence is defined by
Example 2. The numerical results of NM, SM, (4), (5) and (9) are in Table 2 for the following nonlinear functions:
Table 1.
Table 2. Numerical results for solving
5. Conclusion
By theoretical analysis and numerical experiments, we confirm that the proposed method which is a derivative- free two-point method has high computational efficiency. Its convergence order is 3.383 and its efficiency index is 1.839. We can see that the suggested method is suitable to solve nonlinear equations and can also be used for solving boundary-value problems of nonlinear ordinary differential equations.
References
- Ortega, J.M. and Rheinboldt, W.G. (1970) Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, New York.
- Kung, H.T. and Traub, J.F. (1974) Optimal Order of One-Point and Multipoint Iteration. Journal of the ACM, 21, 634-651. http://dx.doi.org/10.1145/321850.321860
- Traub, J.F. (1964) Iterative Methods for the Solution of Equations. Prentice-Hall, Englewood Cliffs.
- Zheng, Q., Wang, J., Zhao, P. and Zhang, L. (2009) A Steffensen-Like Method and Its Higher-Order Variants. Applied Mathematics and Computation, 214, 10-16. http://dx.doi.org/10.1016/j.amc.2009.03.053
- Zheng, Q., Zhao, P., Zhang, L. and Ma, W. (2010) Variants of Steffensen-Secant Method and Applications. Applied Mathematics and Computation, 216, 3486-3496. http://dx.doi.org/10.1016/j.amc.2010.04.058
- Petković, M.S., Ilić, S. and Džunić, J. (2010) Derivative Free Two-Point Methods with and without Memory for Solv- ing Nonlinear Equations. Applied Mathematics and Computation, 217, 1887-1895. http://dx.doi.org/10.1016/j.amc.2010.06.043
- Džunić, J. and Petković, M.S. (2012) A Cubically Convergent Steffensen-Like Method for Solving Nonlinear Equa- tions. Applied Mathematics Letters, 25, 1881-1886.
- Alarcón, V., Amat, S., Busquier, S. and López, D.J. (2008) A Steffensen’s Type Method in Banach Spaces with Appli- cations on Boundary-Value Problems. Journal of Computational and Applied Mathematics, 216, 243-250. http://dx.doi.org/10.1016/j.cam.2007.05.008
NOTES
*Corresponding author.




















