Open Journal of Philosophy
Vol.04 No.01(2014), Article ID:43302,6 pages
10.4236/ojpp.2014.41010
Pythagoras and the Creation of Knowledge
Jose R. Parada-Daza1, Miguel I. Parada-Contzen2
1Universidad de Concepcion, Concepcion, Chile
2Technische Universität Berlin, Berlin, Germany
Email: rparada@udec.cl, miguelparadacontzen@gmail.com
Copyright © 2014 Jose R. Parada-Daza, Miguel I. Parada-Contzen. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Jose R. Parada-Daza, Miguel I. Parada-Contzen. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
In this paper, an approach to Pythagoras’ Theorem is presented within the historical context in which it was developed and from the underlying intellectual outline of the Pythagorean School. This was analyzed from a rationalism standpoint. An experiment is presented to the reader so that they, through direct observation, can analyze Pythagoras’ Theorem and its relation to the creation of knowledge. The theory of knowledge conceptualization is used.
Keywords: Theorem; Pythagoras; Rationalism; Empiricism; Knowledge
Introduction
This paper discusses the creation of scientific knowledge and focuses primarily on the Pythagorean Theorem, which is an un- questioning development from rationalism. The main argument of this paper is that the creation of scientific knowledge has dif- ferent philosophical bases such as rationalism, empiricism, ap- riorism and intellectualism which should coexist when the phe- nomenon is analyzed by the knower.
The particular historical development of Pythagoras’ Theorem as well as that of mathematics in general is addressed, ana- lyzing their approach from a rationalist standpoint but without neglecting other aspects which are evident in said development. Subsequently, the theorem is subjected to direct visual observation by the reader, as an example of empiricism. This is pre- sented to the reader as a practical experiment inciting them to observe the Pythagorean Theorem while briefly abstracting from rational logic. This experiment is an invitation to reflect on how apparent doubts about the validity of knowledge can be genera- ted based solely on the observation of a phenomenon. It should be clarified that the aim of this experiment is not to refute the compliance of such a theorem, but to exemplify how science and, in particular, social sciences which are essentially subject to partial observation, by analyzing differences arising from va- rious philosophical schools, that support the scientific, can hin- der the synthesis of scientific laws with universal validity.
The aforementioned implies that scientific methodology is strongly influenced by the way in which the phenomenon is observed when only direct observation is implemented. That is, in this process the subject is more important than the object of the investigation. The aim of the experiment regarding the Pytha- gorean Theorem is precisely to put the subject over the object in order to ponder its active observation and deliberate on how to defend its perception. It is therefore an invitation to reflection.
From this experiment, the reader is left with conclusions and
observation analysis, even though ideas for discussion are crea- ted by the authors.
The historical development of Pythagoras and the Pythagorean School is outlined within this paper and the different underlying theoretical approaches to the creation of scientific knowledge are also focused upon. Under the latter approach the Pythagoras Theorem is analyzed and the reader is subsequently exposed to a visual observation of the theorem. Some observations from the authors’ stand point are given regarding the experiment.
Pythagoras and the Pythagorean School
The History of Pythagoras and His School
Pythagoras is one of the most well recognized mathematicians, although his figure and influence transcend the strictly ma- thematical. Knowledge of his life and work is not clear howev- er and Boyer (1968) argues that this is due to the fact that many biographies on Pythagoras were written in the distant past and have only partially been preserved up to today. However, the main reason for these doubts is that Pythagoras established an associ- ation based on secrecy among his followers. There are even doubts about what were his direct contributions and what were those by his followers. This is also valid for Pythagoras’ Theorem.
Pythagoras formed a politically conservative school of thought with a strict code of conduct. In this school mathematics, ethics, religion and music were mixed. Pythagoras had differing influences as a consequence of his many travels carried out from the island of Samos, where he was born in 570 AD. He travelled throughout Greece and Egypt and in 520 AD returned to Samos. During one of these trips, he received the influence of the philosopher, scientist, mathematician, and engineer Thales of Miletus. The Pythagorean School was founded in Crotona, today Italy, Boyer (1968). This school was not only an institution where philosophy, mathematics, and natural sci- ences were taught, but also a brotherhood where its members were united for life. In the words of Cajori (1909), “this brotherhood had observances approaching masonic peculiarity”.
Pythagoras and his disciples developed a religious-math- ematic way of thinking of different aspects of their lives from an abstract view point. Mathematics and numbers were central to their interest, and were considered abstract entities, manifested in facts of reality. This approach was followed by Socrates and Plato. In Pythagoras’ school, mathematics, in addition to being the main reason for study, took on a scientific sta- tus.
Pythagoras’ Theorem
Although the theorem is assigned to Pythagoras, there is no record that confirms it was developed directly by him and not by members of his school. The theorem indicates that the square of the hypotenuse of a right triangle equals the sum of the squares of the lengths of the other two sides each one of them called cathetus.
According to Cajori (1909), Pythagoras probably learned the truth of this theorem directly from the Egyptians and the special case of a right angled triangle with sides 3, 4 and 5. Willers (2010), also attributes the theorem to the Babylonians and Indians and indicates that Pythagoras or one of his disciples was the first to encounter a demonstration of this theorem. The de- monstration was developed for strictly geometric concepts that were the basis of mathematics in this period. This is relevant because the demonstration is based solely on the existence of rational (measurable) numbers, which provoked one of the first polemic reactions towards the theorem.
In effect Hippasus of Metapontum, a member the Pythagorean School and a disciple of Pythagoras, showed in parallel that the square root of the number two is an irrational (immeasurable) number, that is, it does not have an exact measure1. According to Pythagoras’ theorem, this is the case of a right triangle with unitary catheti and hypotenuse equal to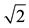 . This could have caused Hippasus of Metapontum to be condemned to death by the Pythagoreans as they could not accept that a number could not be exactly measured. In the ancient concept of Mathematics, numbers were only thought of as positive rational sets and quantities verifiable in physical reality. The con- cept of irrational numbers was developed after geometry through algebra.
. This could have caused Hippasus of Metapontum to be condemned to death by the Pythagoreans as they could not accept that a number could not be exactly measured. In the ancient concept of Mathematics, numbers were only thought of as positive rational sets and quantities verifiable in physical reality. The con- cept of irrational numbers was developed after geometry through algebra.
1To measure means to compare the physical quantity to be measured with a standard canon or “unit” measurement. This is, make the division between the physical quantity and the unit, answering the question “How many times does this unit fit into this quantity?” In this way, if an athletic track has 100 meters, it means that the by making the division between the distance that the athlete runs and a canon known as “meter”, the result is exactly 100. Then, a “measurable” quantity can always be expressed as a rational number (i.e., the quotient between two integers), it is only necessary to consider a small enough standard canon. By definition, an irrational quantity cannot be expressed as the quotient of two integers. Then, as there is not an infinitely precise canon (an infinitely small ruler), there is place to the question: Are irrational quantities representable in our reality?
Rationalism and Empiricism
Hessen’s (1926) perspective is followed in order to analyze the concepts of rationalism and empiricism, which sustains that the production of new knowledge can be found in two opposing viewpoints: rationalism and empiricism. An analysis is also carried out for two intermediate streams between both: apriorism and intellectualism as a mixture of rationalism and empiricism, with a higher influence whatever the case may be.
From a rationalism point of view, the origin of knowledge is in the use of reasoning. As reason has a logical necessity and the creation of knowledge only has origins in thought which implies that knowledge is an idea which generates the concept of idealism. Thus, it is posited that a prior idea exists. It is assumed that Plato was one of the first rationalists. An explanation of this approach is that the world of experiences is in constant change, which implies that real knowledge cannot be produced and have, at the same time, universal validity.
Hessen poses that rationalism arises from mathematics but, on the other hand argues that empiricists would come from na- tural sciences because in said science, experience is the determining factor which generates new knowledge. Empiricism and intellectualism are the basis for methodology and investigation in social and in some natural sciences.
From an empirical perspective, the only root cause of new knowledge is experience without prior influence of reason. Thus, experience prevails over reason in the creation of knowledge. Therefore, all concepts, whether general or abstract, are rooted in experience and not reason. This means that people are not born with prior knowledge and all knowledge is the product of experience and observation of facts.
Between rationalism and empiricism, two other intermediates exist: apriorism and intellectualism.
Intellectualism refers to a school of thought where knowledge comes from the joint use of both reason and experience. In this context, reason creates images of awareness and experi- ence gives rise to concepts. Therefore, intellectualism implies that consciousness extracts from experience and from this, forms concepts. In this combination of rationalism and empiricism, the main emphasis is that there is greater influence from empiricism than rationalism, in the understanding that it is accepted there are logical, universally valid judgments but it is also acknowledged that these judgments come from experience.
On the other hand, another combination of rationalism and empiricism is apriorism in which, it is postulated, that the creation of knowledge comes together with reason and experience, but with greater influence from rationalism than empiricism. It is argued that knowledge has a priori elements which are independent of experience.
This issue has also been discussed in philosophy. Valor-Yé- benes (2001) indicates the presence of absolute objectivism and within the thesis that he proposes as a definition notes: “the identity between the field of being and the field of knowing. Descartes has shown that the whole of what is, does not show more than what is present is as it present”, Valor-Yébenes makes a distinction between fact and necessity, noting that the latter grows from facts, or rather is based in the factual.
Hjørland (2005) states “that it is not a trivial matter to define those epistemologies (empiricism, rationalism and positivism) and to characterize their influence”.
Rationalism, Empiricism and the Pythagorean School
Pythagoras’ way of thinking, not as a person but as the Pythagorean School, within the above scheme has specific aspects of rationalism because, as noted, the Pythagorean way of think- ing is broader than his famous theorem and is related to the conceptual transcendence over the factual. Regarding the latter, it may also be compared to a pure empirical approach for the case of the Pythagorean triple, which is the name given to the numbers three, four and five when they are the sides of a right triangle. These numbers and their representation in a plane can be reproduced and displayed as part of reality, without abstraction or dogma, as the precise reality observed by the senses.
As previously stated, this representation is mistaken for the case of a right triangle whose catheti, each measure a unit. Here, the hypotenuse is an irrational number (immeasurable), as the square root of two is an irrational number. Thus, this issue is not directly observable by the measurement process. Historical literature, sometimes transformed into legend says it was Hippasus of Metapontum, a disciple of Pythagoras, who developed the first geometric proof of the irrationality of the square root of the number two which would have led to him being killed by other sect followers. There are other versions of how he died, but his departure from the school is not discussed, Willers (2010). Michaelides (2008) develops the theme regarding the death of Hippasus of Metapontum.
Thus, Pythagoras’ Theorem also observes an intersection between dogmatism and rationalism, which cannot be excluded as the Pythagorean School was not only mathematical but mix- ed religion and mathematics, thereby generating a cult.
The discovery of Hippasus of Metapontum has important implications for the development of Pythagorean and later Platonic thinking. The physical reality of facts is distanced from the reality of numbers, in finding relationships that could not be expressed in observable physical reality. A triangle with unit catheti has a hypotenuse, which under Hellenic criteria, simply cannot exist. Thus, there was concrete evidence that physical reality is distanced from the ideality of mathematics and that the second does not need the first in order to exist. From here, then, appears an implicit relationship between rationalism and empiricism, almost as a contradiction that bothered the Pythagoreans.
This apparent contradiction is still present in everyday acts. Any electrical engineer (or similar), safely asserts that the voltage tension is an outlet is 220Vac (or 110Vac, depending on the country). This amount would probably be measured with a volt meter. However, the value of 220Vac RMS (Root Mean Square) which is used in engineering is, for sine waves which are theoretically found in an alternating current,
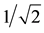 times the value of the wave amplitude. That is, an irrational number which, however, the engineer can measure with an electronic device at a very low market price of around 10 USD. This apparent contradiction is explained rationally, based on the idea that every physical measurement involves an error of both the instrument and measurement process. This fact, accepted as such in the natural sciences, from both an empiricist and rationalist viewpoint does not invalidate a hypothesis. However, when extrapolating the same measurement phenomenon to the human behavioral sciences, where error is difficult to quantify, a gap is left that is not easy to explain from either a rational or an empi- rical standpoint.
times the value of the wave amplitude. That is, an irrational number which, however, the engineer can measure with an electronic device at a very low market price of around 10 USD. This apparent contradiction is explained rationally, based on the idea that every physical measurement involves an error of both the instrument and measurement process. This fact, accepted as such in the natural sciences, from both an empiricist and rationalist viewpoint does not invalidate a hypothesis. However, when extrapolating the same measurement phenomenon to the human behavioral sciences, where error is difficult to quantify, a gap is left that is not easy to explain from either a rational or an empi- rical standpoint.
Received December 30th, 2013; revised January 30th, 2014; accepted February 7th, 2014
While Hippasus of Metapontum’s proof of incommensurability of the root of two is geometric, in continuation a demonstration of the irrationality of that amount is presented which is commonly studied in a basic freshman year algebra course, as it represents a good example of the method of reductio ad absurdum, Vance (1965: pp. 15-16). Let p and q two co-prime integers. That is, two integers that have no common divisor apart from the whole. It is defined that:
 then:
then:
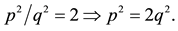 Thus p2 is an even number. With this, p is also an even number, as every square even number has an even root number. Then p = 2n can be written and:
Thus p2 is an even number. With this, p is also an even number, as every square even number has an even root number. Then p = 2n can be written and:
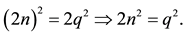 Thus, q2 is also an even number, and consequently, q is an even number.
Thus, q2 is also an even number, and consequently, q is an even number.
This is a contradiction since it is said that both numbers were co-prime integers and we have shown that both are also even numbers. From this contradiction it follows that the root of two cannot be obtained from any two integers when implementing the ratio between them. This result is generalizable to any other non-quadratic value under the root and allows the understanding of the gap between Greek geometry (Pythagorean and Euclidean) and modern analytic geometry and algebra.
There are other notable commonly accepted cases of irrational numbers. For example, the ratio between the diameter and circumference of a circle is irrational and is represented by π ≈ 3.1415926535897932... Also, in The Vitruvian Man by Da Vinci, there is a ratio that is an irrational number, known as the Golden Ratio, Gorman (2002). The ratio between the total height of the Vitruvian Man and the height of his naval results on the irrational number:
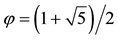 Wilkers (2010). This ratio is associated with the work of the Italian mathematician Fibonacci as the use of the sequence, which bears his name, is a way of obtaining the Golden Ratio by calculating limits of such a se- quence when the number of its terms tends to infinity, Spiegel (1963). This number has had different interpretations in art, ar- chitecture and for example in measuring female beauty, Tahan (1993).
Wilkers (2010). This ratio is associated with the work of the Italian mathematician Fibonacci as the use of the sequence, which bears his name, is a way of obtaining the Golden Ratio by calculating limits of such a se- quence when the number of its terms tends to infinity, Spiegel (1963). This number has had different interpretations in art, ar- chitecture and for example in measuring female beauty, Tahan (1993).
A third case of irrational numbers corresponds to the napierian base of the exponential and logarithmic function, e ≈ 2.71828182846 ... used to model increasing behavior of different types and in different areas of knowledge (demography, economics, statistics, physics and others).
Contemporary notation, in ancient Greece would probably have hindered the compression of the demonstration of irratio- nal numbers as shown above. Indeed, the Indo-Arabic positional numbering of base 10 was developed several centuries (almost a millennium) after Hellenic ascension and was not introduced to Europe until the thirteenth century by the Italian mathematician Fibonacci. The standard algebraic notation for its part, crystallized recently thanks to René Descartes in the seventeenth century. These dates show the slow evolution of human thought and intellectual resistance to changes that occur in society.
Another example of the aforementioned is Zeno of Elea’s dichotomy paradox. The Greek thinker, with a biography as uncertain as that of Pythagoras, dedicated his life to defending the work of his teacher, Parmenides. There are two contributions to the evolution of thought by him and the Eleatic school. The first refers to the dialectical process of contrasting two op- posite versions of the same event and from them build a truth. This is 2300 years before the philosopher GWF Hegel would present his Thesis, Antithesis and Synthesis methodology. The second contribution of the school refers to the first known mention of the idea that would prevail in the coming millennia on infinitesimal calculus. Indeed, Zeno is the first philosopher to describe the physical world in terms of infinitely small time or space. Thus, intending to show it was impossible that physical reality was a reflection of the reality of the numbers, contradic- ting the Pythagorean sect.
Zeno of Elea, faithful to his style of dialect and intent on embarrassing Pythagoras’ followers, posed a series of paradoxes. One is that of Achilles, son of Peleus and the goddess Thetis, Trojan hero and traitor, murderer of Hector and the fastest of men, and a turtle. Zeno argues that not even Achilles could reach a turtle, the slowest animal in the world, if it were given a head start in a race. This was because when Achilles reached the position where the turtle was at the start of the hero’s race, it would have already advanced a certain distance. Then Achilles would reach the turtle’s new position, but it would have moved a further distance again obtaining the lead and thus extending the procedure infinitely, with increasingly smaller distances and Achilles always finding himself behind the turtle. This paradox is not very complex in the scheme of current thinking, but it was a puzzle to the Hellenic world. This paradox is an example of generating knowledge by direct observation.
The second of Zeno’s paradoxes is a variation of the aforementioned called the dichotomy paradox. If a stone is thrown from one point to another, it first must travel half of the distance, leaving the second half still to be travelled. Secondly, the stone must then travel half of the remaining distance or a quarter of the initial distance, still leaving half of the distance previously travelled. Then, the stone must again travel half of the remaining distance or an eighth of the initial distance, and there would still be remaining half of the new distance to be travelled. In this way the stone would never reach its destination thus making any type of movement impossible. With this, Zeno tried to show that the physical world does not exist as such and was just a projection from within each individual and not an abstract reality like Pythagorean numbers. There is also a higher incidence of empiricism, or observation of reality.
While Archimedes worked in the Third Century, BC with the idea of infinite sums similar to those which comprise modern calculus, Cajori (1909: 35), the mathematical language that en- ables efficient and thorough dissemination of the solution to Zeno’s paradox was not decided until the XVII century with the formal discovery of infinitesimal calculus. According to Cajori (Op.Cit.), Archimedes, in regards to infinitesimals, indicates that: “infinitesimals (infinitely small constants) were not used in rigorous demonstrations” Furthermore, it is stated that Archimedes “considered infinitesimals sufficiently scientific to suggest the truths of theorems, but not to furnish rigorous proofs”. One of the authors of this paper, working as a mathematics Teachers Assistant to freshman year engineering students, presented this exercise with excitement and enthusiasm, thus in just one line giving evidence of two millennia of mankind’s intellectual evolution. Unfortunately, none of the students were as interested or motivated as the Teacher Assistant.
The solution posited in continuation as the finite sum of a geometric progression with the first term
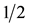 and also with the ratio
and also with the ratio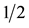 . The distance traveled by the stone thrown by Zeno is represented by l. This is exhibited in the next expres- sion:
. The distance traveled by the stone thrown by Zeno is represented by l. This is exhibited in the next expres- sion:
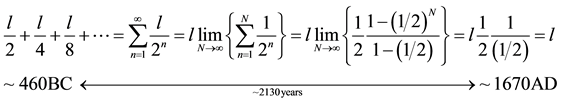
Taking the process to infinity, the stone would finally travel the desired distance l invalidating Zeno’s thesis. This simple exercise is a fairly elegant way of introducing the concept of limit and takes advantage of the formula for the sum of the first N terms of a geometric progression. However, from Zeno’s original approach, circa 460 BC, through Archimedes’ numerical approximation methods, until it was possible a formal approach, rigorous and universal solution to the paradox, after 1670 AD, it took at least 2130 years, which shows the long pe- riod of creation and consolidation of knowledge, for this particular case.
The slow pace with which societies recognize intellectual changes that lead to abstraction as the basis of thought not only ended Hippasus of Metapontum’s life 2500 years ago but interestingly also had consequences for James A. Garfield, the twentieth president of USA and amateur mathematician. Garfield was the second US president assassinated while in office after Abraham Lincoln. Prior to his tenure, he developed and published one of the many proofs of Pythagoras’ Theorem, available in basic math texts. This was done through the formation of a trapezoid, within three rectangle triangles inscribe and using an area calculus exercise and algebra to prove the theorem.
A proof of the theorem similar to that of President Garfield, is the following, Wilkers (2010): Consider the square in Figure 1 which consists of four right triangles with legs a and b and hypotenuse h joined at their vertices. The area of said square
corresponds to the square of one side, namely: A = (a + b)2. Moreover, the area of the square also corresponds to the sum of the area of each of the four right triangles that comprise the square of side h formed in the center of the figure. That is: . Equating both expressions and reducing terms, we have the following:
. Equating both expressions and reducing terms, we have the following: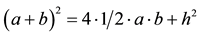 , then: a2 + 2ab + b2 = 2ab + h2, then: a2 + b2 = h2.
, then: a2 + 2ab + b2 = 2ab + h2, then: a2 + b2 = h2.
With this, the validity of a theorem discovered more than two millennia ago is proved.
Square constructed with 4 triangles.
The cause of Garfield’s assassination goes beyond strictly political reasons and is related to the personal revenge of a North American lawyer whom was denied (unjustly in his opinion) a diplomatic post in Paris. As a product of his strange and incoherent reasoning as well as his erratic and aggressive behavior, it is speculated that Garfield’s murderer suffered from a major mental illness that led him to commit the crime. Paradoxically, it is possible that the two bullets that Garfield recei- ved could not have caused his death in the absence of assistance from multiple physicians. In the late nineteenth century, surgical equipment sterilization was not a common practice in medicine and was not fully accepted by the specialized society. Moreover, in the case of bullets, priority was given to extracting the projectile as soon as possible and at any cost. Therefore, during the seventy days that Garfield agonized, many doctors introduced their unsterilized fingers into the president’s wound trying to remove the foreign body. In this way, a relatively small wound became a fatal infection which finally killed the president on September 19, 1881.
Garfield’s death also shows the resistance to accept new ideas that occurs in society that break with established thought patterns, in this case in regards to medical ideas. In mathematics, this first occurred with irrational numbers, with zero (absurd in the Euclidean geometric design), with negative numbers and finally with imaginary and complex numbers. In other disciplines, such as the physics of Copernicus, Newton and Einstein, philosophical debates forced humanity to completely change its view of things. However, this resistance is often justified and grounded.
As shown above, the cited theorem is a truth in itself. Pythagoras’ Theorem, as any geometry freshman knows, is an irrefutable truth and universally accepted as such. Could there be any doubt? Respect to empiricism and its relation with Pythagoras’ theorem, Hessen’s work warrants mentioning. This indicates that Hume, who developed Locke’s empiricism, recognizes that mathematical knowledge is independent from experience and therefore universally valid. However the relationships between mathematical concepts are valid, independent of all experience. It is indicated that “the propositions that these relationships express, i.e., Pythagoras’ Theorem can be discovered purely through the activity of thought and do not depend on anything that exists in this world. Even if a triangle had never existed, the truths demonstrated by Euclid would al- ways conserve their certainty and proof”, Hessen (1993: pp. 64-65).
In the following, the theorem is subjected to an empirical experiment so that each observer obtains its conclusions according to their own perception of the facts.
An Experiment on Pythagoras’ Theorem
Pythagoras’ Theorem, from a theory of knowledge point of view, is primarily based on a strand of rationalism and therefore can be considered a universal law whose compliance is irrefutable by rational methods. This paper addresses the facts relating to the theorem through observation of reality, or rather, the use of empiricism where knowledge is obtained through direct observation of a phenomenon, captured by the sensory organs of the experimenter. Therefore, this is an experiment principally supported by fact.
The proof discussed below indicates that there are some points of the theorem that are difficult to understand when only the visual perception of the observer is relied upon. The aim of this experiment is not to create direct knowledge, but to present that an example of the fact that the truth about a given phenomenon depends on “the eye of the beholder” which is a typical situation in human behavioral sciences. The following exercise is intended to create research questions regarding the Theorem and also on how knowledge is generated based solely on direct process observation.
The proposed experiment consists of taking two rectangular sheets of paper of the same size (two sheets of printer paper). (see Figure 2).
The experiment involves the following steps:
Step 1. Take two rectangular sheets of paper of the same size (two sheets of printer paper) as shown in Figure 3, placing sheet No 1 onto sheet No 2.
Step 2. Verify, superimposing one page onto the other, that they are the same length (or width), as shown in Figure 4. This means that:
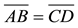 on Figure 2.
on Figure 2.
Step 3. Join the corners, making them coincide so that the sheets of paper overlap exactly and that there seems to be single sheet of paper, as shown in Figure 5.
Step 4. With your fingers, slowly and carefully rotate the top sheet of paper, using corners
 as a pivot (see Figure 6). Figure 2 shows that with the displacement, an ABH or CDH right triangle is made.
as a pivot (see Figure 6). Figure 2 shows that with the displacement, an ABH or CDH right triangle is made.
Step 5. Measure with a ruler the segments
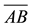 y
y .
.
Sheets No 1 and No 2 with their respective vertices.
Step 1 of the exercise.
Step 2 of the exercise.
Step 3 of the exercise.
Step 4 of the exercise.
Once familiar with the experiment, answer the following questions:
1. Are you familiar with the following mathematical expression: c2 = a2 + b2?
- Yes - No
2. The mathematical expression above represents:
1) Pythagoras’ Theorem, where “a” and “b” are the catheti of a right triangle and “c” is the hypotenuse
2) The square of the binomial
3) An equation whose unknown is “c”.
3. Have you ever doubted the compliance of the expression in question 1?
- Yes - No
4. In the proposed experiment, have you visually checked that the upper widths of the two sheets are exactly the same? That is:
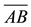

- Yes - No
5. In the proposed experiment with the sheets of printer paper, moving vertex B of the top sheet from D, downward from the lower sheet. Do you observe the following?
1) Vertex B remains precisely fixed to the vertex edge of the other sheet D to a point where vertex B inclines toward the left side (where B = H) and away from the edge of the second sheet (whose vertices are C and D).
2) Vertex B is never attached to the edge of the second sheet (with vertexs C and D).
3) Moving point B from point D of the bottom sheet, this (Vertex B) continues in the same direction as an inscribed circle whose radius is equal to the width of both sheets.
6. If in the previous answer (5), you accept the affirmation 1), according to your vision, the following should be present- ed:
1) Something absurd because, according to Pythagoras’ Theorem, this is an impossible situation.
2) That your vision is impaired and you cannot see the lines precisely. Should you go to an ophthalmologist?
3) You have visual doubts about Pythagoras’ Theorem
4) You should repeat the experiment several times because you have doubts about what you see.
7. If you repeat the experiment several times, do you see the same thing?
- Yes - No - Sometimes yes and sometimes no
8. If your answer was Number 7: “Sometimes yes and sometimes no,” What is the most predominant in your visual perception?
- Yes - No
Author’s Comments about the Experiment
Repeating Step 4 the following observations arise, depending on the point of view of the experiment. This exposes some ideas about the experiment and obviously invites the reader to analyze the discussion of knowledge generation. It is not intended, through these observations, to influence the reader’s vision and their conclusions.
It can be observed that a very acute ABH or CDH triangle is generated. The rectangle displayed in Figure 2 shows that from a point on the right side of the two sheets (Vertex H), the vertex of the top sheet starts to move away from point H on the right side of the sheet below and remains fixed. If this figure is observed, it would indicate that the upper side of both sheets have the same length
sheet, the side

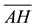
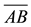
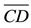
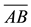
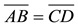
If this is observed it gives rise to a central question: Is Pythagoras’ theorem only valid for some cases and would not be a general rule but a particular case when verified with a direct observation method based on empiricism? From a rationalism stand point, the test shown here does not have validity, however from an empiricism standpoint doubt arises for those who observe the presence of this triangle. In effect, visual observation would have a concrete answer through the concept of measurement error. The latter can be quantified using the theorem and the ratio between the height and the base of the triangle, allowing an empirical explanation as an observation of an imprecise measurement process.
Following the empirical method it would be necessary to repeat this case with many people and analyze the view of each one. This is the challenge that is posited in this paper. Obviously in order to respond to this empiricist concern the use of rationalist dogma is not necessary.
Some considerations could be given to the above explanations such as: imperfections in the sheets of printer paper, impressions caused by using a vertex as a pivot, measurement error, trigonometric errors when working with very small angles. Myopia, astigmatism and other variables that affect the observer’ senses could also be influences.
Conclusion
The answer to the proposed problem is not simple, because it is the basis of how knowledge is generated, if through what the observer brings incorporated in their mind and reasoning a pri- ori or processed in their brain what their sensory organs capture. This paper is not intended to generate an answer but to plant a doubt about the proposed problem as any observer could see a distinct reality.
The observations invite reflection on some scenarios. One position is that the Pythagorean result, from rationalism, is re- affirmed and another position could create a hypothesis in the sense that proof could be seen that physical reality does not necessarily behave in the same way as mathematical abstraction. Therefore, it could be contemplated. For some, the exercise po- sited, could also generate, among others, a doubt with respect to irrefutability of Pythagoras’ Theorem. From this the following questions arise: Is it reality perhaps that we can and want to observe? Does the empiricist method leave everything up to the perception of the researcher, the main problem of social and experimental sciences that complicate the validity of universal and irrefutable scientific law.
From a rationalist point of view, whether in mathematics or engineering, as in the aforementioned examples, what is proposed herein as a visual experiment of a theorem, does not pre- sent doubts because the differences can be satisfactorily explain- ed by measurement error. However, with behavioral sciences such as economics, sociology, psychology, such error is difficult to perceive quantitatively when the phenomenon is directly observed by the researcher, even when mathematical formality is used to describe the phenomenon. Thus, in these sciences the performance and perception of the subject studied, i.e., the observer, has a major influence on the creation of knowledge. In these latter sciences, the external perception of the phenome- non becomes crucial for the creation of knowledge.
References
- Boyer, C. B. (1968). A history of mathematics. New York, London, Sy- dney: John Wiley & Sons, Inc.
- Cajori, F. (1909). A history of mathematics. London: The MacMillan Company, Macmillan & Co. Ltd.
- Gorman, M. J. (2002). Leonardo’s vitruvian man. This site was created as a final project for Michael John Gorman’s STS 102: “Leonardo: Science, Technology, and Art” at Stanford University, Fall. http://leonardodavinci.stanford.edu/submissions/clabaugh/history/leonardo.html
- Hessen, J. (1993). Teoría del conocimiento. Editores Unidos, México. Original Text in German: Erkenntnistheorie, Ferd. Dümmlers Ver- lagsbuchhandlung, 1926, Berlin.
- Hjørland, B. (2005). Empiricism, rationalism and positivism in library and information science. Journal of Documentation, 61, 130-155. http://dx.doi.org/10.1108/00220410510578050
- Michaelides, T. (2008). Pythagorean crimes. Las Vegas: Parmenides Publishing.
- Spiegel, M. R. (1963). Advanced calculus. New York: Schaum Publish- ing, McGraw-Hill Book Company. 55.
- Valor Yébenes, J. A. (2001). Empirismo y Objetividad. Thémata. Re- vista de Filosofía, Número 26, 123-156, España.
- Vance, E. P. (1965). Modern college algebra. Addison-Wesley, 15-16.
- Willers, M. (2010). The bedside book of algebra. London: Quid Publi- shing.
- Tahan, M. (1993). The man who counted. New York: W.W. Norton & Company, Inc.







