Received 5 November 2015; accepted 12 February 2016; published 16 February 2016

ABSTRACT

The worship places in India are usually situated in and around the hilly regions and/or mountainous area and a number of devotees used to visit the holy places in every area for worship. The stability slopes upon which these worship places are located in the hilly and mountainous region are always a major concern. Moreover, heavy precipitation, weathering conditions, seismic disturbances and human activities could cause problem to the stability of such slopes. The effect of slope instability could cause delay in traffic, loss of life of the devotees at pilgrim sites and the loss of the properties. The Saptashrungi gad temple (SGT) situated on basaltic hills belongs to Deccan volcanic and is one among the 51 Shakti Peeths and the most holy place for pilgrims. In this research, the slope stability analysis at SGT hill is assessed using Phase 2, a finite element program along the two parikrama paths: Parikrama Path 1 (or the Badi Parikrama Path “BPP”), and Parikrama Path 2 (or the Chhoti Parikrama Path “CPP”). On the basis of extensive field work, topographic survey, complex geology, orientations of joint sets, hill slope faces and geotechnical conditions, the study area has been divided into eight zones (Zone#01 to Zone#08), and eighteen topographic profiles (AA′ to RR′) are taken from these eight zones for detailed slope stability analysis. The analysis helps to identify the potentially vulnerable slope and zone of instability.

Keywords:

Saptashrungi Gad, Stability, Phase 2, Finite Element

1. Introduction

Natural slopes are omnipresent on earth surfaces with slope inclination varying from near zero to almost vertical. Also, man-made slopes can be created by excavation activities such as building, roadways, railways and highways. The failure of these slopes occurs whenever an imbalance takes place between shear strength and shear stress in the ground and causes enormous loss of life as well as properties. The triggering factors for slope failure could be linked to heavy precipitation, weathering conditions, seismic disturbances and human activities [1] - [5] .

Stability analysis of rock slopes is carried out to assess the safe and economical design of slopes and/or to assess the equilibrium conditions of the slopes. The method selected for stability analysis depends on site condition and potential mode of failure with special consideration given to strength, weakness and limitation of each methodology. The main objectives of these stability analyses are: 1) to investigate the potential failure mode; 2) to determine slope stability conditions; and 3) to design safe and economical slopes. In present time, n-number of slope stability analysis tools are available for rock slope as well as rock-soil mixed slopes; these range from limit equilibrium technique (simple infinite slope) to sophisticated couple finite distinct codes or couple distinct element codes. However, these slope stability methods can be discussed under three categories such as conventional, numerical and probabilistic [1] [2] [6] - [10] .

Kinematic analysis and limit equilibrium techniques come under conventional slope stability methods. Numerical methods of analysis for rock slope stability investigation can be divided into three methods: 1) continuum modeling; 2) discontinuum modeling; and 3) hybrid modeling. Continuum method used in stability analysis includes finite element methods (FEM) and finite difference method (FDM), which is applicable for the slopes comprised of massive to soil-like or heavily fractured rock masses. In discontinuum modelling, rock slope is considered as discontinuous rockmass by considering it as an assemblage of rigid or deformable blocks with discontinuities represented explicitly (having specific attitude and position). Several variations of the discrete-element methodology exist as: 1) distinct element method (DEM); 2) discontinuous deformation analysis (DDA); and 3) particle flow codes (PFC) [11] . Nowaday’s hybrid approaches are very popular for rock slope stability as adopted in the GEO-SLOPE program. The techniques combined analyses such as limit equilibrium stability analysis, finite-element groundwater flow and stress analysis. The latest advancement of the use of hybrid technique includes coupled particle flow and finite-difference analyses that used in program like FLAC2D and PFC3D [12] .

In this research, the slope stability analysis at SGT hill is assessed using Phase 2 [13] , a finite element program along the two parikrama paths, i.e. Parikrama Path 1 (or the Badi Parikrama Path “BPP”) located at the toe of the SGT hill, and Parikrama Path 2 (or the Chhoti Parikrama Path “CPP”) located 200 m above the BPP (Figure 1). On the basis of extensive field work, topographic survey, complex geology, orientations of joint sets,

hill slope faces and geotechnical conditions, the study area has been divided into eight zones (Zone#01 to Zone#08), and eighteen topographic profiles (AA′ to RR′) are taken from these eight zones for detail slope stability analysis (Figure 1).

Representative rocks samples have been collected from the study area and the samples have beed tested in the laboratory as per the established standard procedures. The experiments were done to estimate the essential input parameters for slope stability analysis (point load strength index, uniaxial compressive strength, tensile strength, slake durability index, young modulus, Poisson’s ratio, density and porosity) of rocks.

The study helps to identify the stability of the slopes using FEM method at SGT hill that is further used to define economical protection measures.

2. Location and Geology of the Area

The Saptashrungi Gad Temple (SGT) lies in Vani village of Nashik district, Maharashtra, India. The SGT hill situated on the top of the hill range known as Saptashrungi. SGT is a holy place for the pilgrims and every year large number of devotee used to come for Devi Darshan and to perform parikrama along both the parikrama paths. The study area is located between latitude 20˚23'05" - 20˚23'55" and longitude 73˚54'05" - 73˚54'30" and comes within the topo-sheet no. 46H/15 allocated by the Survey of India (SOI). The study area can assess through the National Highway (NH)-3 and then by a State Highway (SH)-17 to reach SGT hill located near the village of Vani (Figure 2). The topographic survey revealed that the highest elevation is 412 m (M.S.L.) for the SG hill and the lowest elevations in the study area is 500 m (M.S.L.) for “para” river course. The annual rainfall is 98.1 mm to 146.1 mm in the month of June to September with maximum of 206.4 mm in July [14] .

The residual hill ranges and the intermediate valleys are well developed on a tableland surface, forming the main geomorphic element of the landscape in the area. About, 60 million years ago, the outpouring of basic lava through fissures formed horizontally bedded basalt over large regions. Variations in their composition and structure have resulted in massive, well-jointed steel-grey cliff faces alternating with structural benches of vesicular amygdaloid lava, all of which contribute to the pyramidal-shaped hills and crest level plateau or mesas. The area exposes thick pile of basaltic flows with a number of basic and rare acid intrusive belongs to Deccan Volcanic of Upper Cretaceous to Lower Eocene age of Sahyadri Group. The entire lava flow has been separated into three formations viz. Salher Formation, Lower Ratangarh Formation and Upper Ratangarh Formation in ascending order of the Sahyadri group (Figure 3). The lower most, Salher Formation, is conspicuously dominant in the lower reaches and mainly consists of compound flows. The overlying thick pile of largely compound flows known as Lower Ratnagarh Formation and the next overlying group of compound flows exposed is called as Upper Ratnagarh Formation [15] - [17] .

The SGT hill is extensively investigated for structural parameters and found that the study area has multi- oriented joint patterns with three sets plus random orientations at the majority of the locations. In addition,

wedge failures were noticed throughout the hill as shown in shown in Figure 4(b)-(c). References [14] [17] reported a rockfall hazard analysis and risk assessment respectively. The authors have identified rockfall prone zone(s) and suggested some valuable protection measures.

3. Field Observations and Slope Stability Analysis

Field observations help to identify the geological conditions of the study area along with the degree of weathering, joint orientations and slope stability problems. Also, representative rock samples collected during field investigations for the determination of physico-mechanical properties in the laboratory as per the methods suggested by ISRM [18] . A detail scan line survey revealed number of discontinuities at different locations. Also, the discontinuity surfaces are rough in nature and no water seepage has been observed in the study area.

Finite element models are computer based program, tries to characterize the mechanical behavior of a rockmass with a set of initial conditions, i.e. boundary, in-situ stresses and water conditions. The models divide the rockmass into zones and each zone comprising material model and properties. The role of material model is to describe how the material behaves (stress/strain relations). The factor of safety (FOS) defined as the ratio of actual shear strength to the minimum shear strength required to prevent slope failure. The logical way to compute FOS with finite element method is to reduce the shear strength until the collapse occurs and termed as shear strength reduction (SSR) technique first introduced by Reference [19] . The advantage to use the SSR technique

over limit equilibrium slope stability is two folds: i) SSR automatically identify the critical slip surface and no need to specify the shape of the sliding surface, and ii) SSR technique automatically satisfy translational and rotational equilibrium, which has not available in some of the limit equilibrium techniques.

Moreover, it is required to artificially truncating the infinite extent of a real problem domain to include the immediate area of interest in slope stability analysis. To overcome this difficulty Reference [20] introduced a recommendation shown in Figure 5 for artificial far field boundary condition, as it does not significantly affect the stability results. The second most important parameter in slope stability analysis is the presence of discontinuities. Also, in a large slope, it is practically impossible to incorporate all discontinuities. So, to overcome this difficulty, discontinuities are introduced by the reduction of intact rock elastic properties such as rockmass strength (σ_cm), the rockmass deformation modulus (E_m) and the rockmass constants (m_b, s and a) using Roclab program based on generalized Hoek-Brown failure criterion [21] [22] . The equation for the generalized Hoek Brown criterion for jointed rockmass is expressed by the equation below:

(1)

where 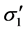= minimum effective principle stress at failure, = maximum effective principle stress at failure, = uniaxial compressive strength of the intact rockmass, m_b = value of the Hoek-Brown constant m_i for the rockmass, given by,

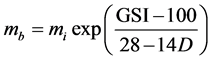(2)

s and a = constant factors, depending on the rock mass properties, given by:

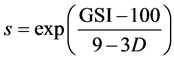(3)

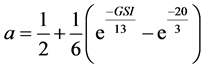(4)

Geological strength index (GSI) value can be obtained by comparing the quantitative GSI chart with the condition of the exposed rock mass identified by visual inspection [23] . Also, rockmass constants are evaluated using equations 2, 3 and 4 with the value of basaltic material constant (mi) and the value of D, a factor that depends upon the degree of disturbance to which the rockmass is subjected to by blast damage and stress relaxation tests is considered as zero, indicating absence of blasting. Lastly, equivalent Mohr-Coulomb parameters for the basaltic rockmass were calculated using the Hoek-Brown failure envelope and tabulated in Table 1.

4. Results and Discussion

During the extensive field visit, it has been found that the SGT hill was highly jointed and deformed with more than three joint sets (Figure 4). These joints were closely spaced and persistence. Moreover, heavy rainfall during June to September also serves as a triggering agent for slope instability [14] .

Slope stability for SGT hill was performed along 18 profiles (AA′ to RR′) distributed in eight zones. The Phase 2 program has been used to do the FEM simulations. Uniform mesh with 6 node triangular and approximately 1500 mesh elements was constructed to divide the slope geometry. Also, plain strain analysis type with Gaussian elimination solver has been used with maximum number of iterations as 500 and tolerance as 0.001. Phase 2 can allow the user to choose if the material can behave like an elastic and/or plastic material for slope stability analysis. So, for the present study plastic material type has been chosen, indicating that the material can yield/fail. Initial element loading is set to gravity field stress and body force (both in-situ stress and material self-weight is applied). Table 1 lists all input parameters used for Phase 2 numerical modelling and detail analyses for each zone discussed below:

A) Zone#01

The zone#01 comprises of four profiles EE′, FF′, GG′ and HH′. The profile HH′ is along the temple. The FEM analyses have been shown in Figure 6(P1)-(P4). The SSR indicates that the slope is stable with maximum FOS 4.84 for profile GG′ and a minimum 1.75 for profile EE′. The temple profile HH′ has a maximum total displacement and strain value (Figure 6(P4c&d)), whereas, minimum total displacement and strain value is for profile GG′ (Figure 6(P3c&d)).

B) Zone#02

Profiles CC′ and DD′ come in zone#02 with FOS > 2.0, suggested stable slopes respectively. The maximum total displacement is >1.0 cm for CC′, whereas, for DD′, greater than 1.5 cm. Figure 7(P5c) for profile CC′ shows the development of displacement above the CPP; however, decreases below CPP due to gentle slope and also, the same results were observed for profile DD′ (Figure 7(P6c)).

C) Zone#03, Zone#04 and Zone#05

Each zone comprises of a single profile, i.e. profiles BB′, AA′ and RR′ respectively. The analyses indicate a stable slope condition with FOS 2.36 for profile BB′, 1.75 for profile AA′ and 1.59 for profile RR′ respectively. In addition, among the three profiles, BB′ has least maximum total displacement with value less than 0.001 mm (Figure 8(P7c)). Furthermore, profile AA′ and RR′ has a maximum total displacement with 0.30 cm and 0.95 cm respectively (Figure 8(P8c) and Figure 8(P9c)). The development of strain in these three zones is above the stable limit and causing no harm to slope stability.

D) Zone#06

The results of the numerical analysis for profile PP′ and QQ′ are shown in Figure 9(P10)-(P11). Profiles PP′ and QQ′ has FOS 3.06 and 2.20 respectively, and as per FOS values, the slope is highly stable; however, for profile QQ′, the maximum total displacement is >2.0 cm (Figure 9(P11c)), concentrated at the top of the hill. Although, the value of maximum total displacement for profile PP′ has a value of 0.67 cm (Figure 9(P10c)),

concentrated at the top portion of the hill (only 35% of the total slope height), suggested no sign of instability.

E) Zone#07

This zone comprises of profiles MM′, NN′ and OO′ and the results shown in Figure 10(P12)-(P14). Based on numerical analysis, it has been observed that FOS is >2.5 for slope MM′ and OO′, whereas, >2.0 for slope NN′ and signifying safe slope. However, slope NN′ has the least value of FOS, causing higher value of maximum total displacement.

F) Zone#08

The left zone of SGT hill has profiles II′, JJ′, KK′ and LL′. Among the four profiles, two profiles II′ and JJ′ has FOS >2.5 (Figure 11(P15b&P16b)), whereas, other two profiles KK′ and LL′ has FOS values >3.0 (Figure 11(P17b&P18b)). In addition, only one profile II′ shows maximum total displacement of the order of 1.24 cm (Figure 11(P15c)) and the rest of the profiles have the value equal to or greater than 0.30 cm.

The FEM analyses provide the FOS, shear strain and total displacement pattern along the slope profiles. Magnitude of above parameters has been on the safe side, with FOS values range from 1.59 to 4.84, the maximum shear strain varies from 0.0003 to 0.0017 and the maximum total displacement varies from 0.0008 cm to 2.40 cm (Table 2). The variations in output parameters indicate that the stability of the slopes was not uniform throughout the SGT hill and can be divided into three categories as per FOS and visual observations during field investigations. In this regard, FOS between 1.50 and 2.00 is categorized as safe with requirement of minor slope protection; the FOS between 2.00 to 2.50 is safer with requirement of few local slope protections and FOS more than 2.50 FOS is categorized as very safe.

The critical slope profiles have been identified as EE′ and FF′ of Zone#01, AA′ of Zone#04 and RR′ of Zone#05. The FOS of these profiles was in between 1.50 - 2.00, indicates safer slope conditions with the minor requirement of repairment of the slopes. However, profile RR′ shows maximum total displacement of about 1.0 cm, indicating a chance of failure if the strength of the material further decreases.

The FOS between 2.00 to 2.5 were obtained for profile HH′ of Zone#01, CC′ of Zone#02, BB′ of Zone#03, QQ′ of Zone#06 and NN′ of Zone#07. As per visual observations during field survey and numerical analysis, these slopes were safe. However, numerical analysis of section HH′ of Zone#01 showed the maximum total displacement >1.0 cm which indicates a chance of failure, if strength of material decreases. Other slopes such as DD′, II′, JJ′, MM′, OO′, SS′, KK′, LL′ and PP′ of respected zones were identified as very safe as per numerical analysis.

Although finite element analyses provide majority of slopes are stable in nature; however, given that rockfall is a frequent happening at the SGT hill, 2D and 3D rockfall studies have been performed at SGT hill [14] [17] .

5. Conclusions

The present study deals with the study of the slope stability using the FEM method at SGT hill. It is concluded

The color code is based on the values of maximum total displacement for less than and greater than 1.

that the advertently field investigation/survey is the foremost and very important exercise to understand the conditions and the nature of the slopes. Keep this in mind during field observations; every location has been carefully investigations. Vulnerable slopes were identified using lithological nature and characteristics of the discontinuities in different parts of the SGT hill that helps to categorize the study area into eight zones. The FEM analysis indicates that FOS varies from 1.59 to 4.84 representing stable slope. The maximum shear strain varies from 0.0003 to 0.0017. The maximum total displacement varies from 0.0008 cm to 2.40 cm. However, for section CC′, DD′, HH′, II′ and QQ′, the maximum total displacement is greater than 1.0 cm and any local or global disturbance may cause decrease in material strength, ultimately resulting in localized slope failures.

The fracture pattern identified during the field visit indicated the problem of rockfall, which had been reported by References [14] [17] and some of the protection measures had been proposed. Also, the proposed protection measures have already been installed in some part of the SGT hill and it has stopped/minimized the falling of rocks.

Cite this paper

Mohammad KhalidAnsari,MashudAhmad,RajeshSingh,Trilok NathSingh, (2016) Slope Stability Assessment of Saptashrungi Gad Temple, Vani, Nashik, Maharashtra, India—A Numerical Approach. World Journal of Engineering and Technology,04,103-115. doi: 10.4236/wjet.2016.41010

References