World Journal of Engineering and Technology
Vol.2 No.2(2014), Article
ID:46330,18
pages
DOI:10.4236/wjet.2014.22015
Numerical Study of Slip Effect of Unsteady MHD Pulsatile Flow through Porous Medium in an Artery Using Generalized Differential Quadrature Method (Comparative Study)
Islam M. Eldesoky1, Mohamed H. Kamel2, Ramzy M. Abumandour1*
1Department of Basic Engineering Sciences, Faculty of Engineering, Menofia University, Shebien El-Kom, Egypt
2Department of Engineering Mathematics and Physics, Faculty of Engineering, Cairo University, Giza, Egypt
Email: *ramzy_0000@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2014; revised 13 May 2014; accepted 20 May 2014
Abstract
The unsteady pulsatile flow of blood through porous medium in an artery has been studied under the influence of periodic body acceleration and slip condition by considering blood as incompressible Newtonian electrically conducting fluid in the presence of magnetic field. In this paper, a new technique of differential quadrature method is introduced to find numerical solution of nonlinear partial differential equations such as the equation of motion of this problem “Navier-Stokes equation”. The presence of the nonlinearity in the problem leads to severe difficulties in the solution approximation. In construction of the numerical scheme “a new algorithm” a generalized differential quadrature method (GDQM) is to use for derivatives with respect to space variables of differential equations and for the time derivative applying fourth order Runge-Kutta Method (RKM). The GDQM changed the nonlinear partial differential equations into a system of nonlinear ordinary differential equations (ODEs). The obtained system of ODEs is solved by 4th order RKM. This combination of DQM and 4th order RKM gives a very good numerical technique for solving time dependent problems. The algorithm is coded in Matlab 7.14.0.739 and the simulations are run on a Pentium 4 CPU 900 MHz with 1 GB memory capacity. The effects of slip condition, magnetic field, porous medium, and body acceleration have been discussed. The numerical results show that the proposed method is more accurate and convergent than other numerical methods in literature. The method is illustrated and compared with the exact and analytical solutions and it is found that the proposed method gives a better accuracy and is quite easy to implement.
Keywords:Pulsatile Blood Flow Magnetic Field, Body Acceleration, Porous Medium, Differential Quadrature Method, Runge-Kutta Method

1. Introduction
Numerical approximation methods for solving partial differential equations have been widely used in many fields of science, particularly in physics, engineering, chemistry and finance, and are fundamental for the mathematical formulation of continuum models. Most numerical simulations of engineering problems can be currently carried out by conventional low order, classical techniques, such as finite element and finite difference methods are well developed and well known. These methods can provide very accurate results by using a large number of grid points. However, in some practical applications, the numerical solutions of partial differential equations are required at only a few specified points in the physical domain. For acceptable accuracy, the conventional low order technique still required the use of a large number of grid points to obtain accurate solutions at these specified points. In seeking a more efficient method using just a few grid points to obtain accurate numerical results, the technique of differential quadrature method (DQM) was proposed by Bellman [1] [2] . The DQM is a numerical solution technique for initial and/or boundary value problems. The DQM is an easy and efficient numerical method for the rapid solution of various linear and nonlinear differential and integro-differential equations. The DQM circumvents the above difficulties by computing a moderately accurate solution from only a few points. For more details see [3] . The DQM follows the concepts of classical integral quadrature. The DQM discretizes any derivative at a point by a weighted linear sum of functional values at its neighboring points. The key to DQ is to determine the weighting coefficient for any order derivative discretization. Bellman et al. [2] suggested two methods to determine the weighting coefficients of the first order derivative. The first method used a simple function as test functions to solve an algebraic equation system. The second method is similar to the first one with the exception, but with the coordinates of grid points chosen as the roots of the shifted Legendre polynomial. Most pervious application of DQ in engineering use Bellman’s first method to obtain the weighting coefficients because it lets the coordinates of grid points be chosen arbitrarily. Unfortunately, when the order of the algebraic equation system is large, its matrix is ill-conditioned. Thus it is very difficult to obtain the weighting coefficients for a large number of grid points using this method. To overcome the drawbacks of the above methods, Quan and Chang [4] , Shu and Richards [5] and Wen and Yu [6] derived a recursive formula to obtain these coefficients directly and irrespective of the number and positions of the sampling points. In their approach, they used the Lagrange polynomials as the test functions and found a simple recurrence formula for the weighting coefficients for the first and second order derivatives discretization. More generally, Shu and Richards [7] , and Shu [8] present the generalized differential quadrature (GDQ). In GDQ, the weighting coefficients of the first order derivative are determined by a simple algebraic formulation without any restriction on choice of grid points, and the weighting coefficient of the second and higher order derivatives are determined by a recurrence relationship. The major advantage of GDQ over DQ is its ease of the computation of the weighting coefficients without any restriction on the choice of grid points. The pioneer works for the applications of the DQM to the general area of structural mechanics and fluid mechanics. To solve these equations, the boundary conditions have to be implemented appropriately. For the case where there is only one boundary condition at each boundary, the implementation is very simple and can be done in a straightforward way. However, in some cases, there is more than one boundary condition, which could result in difficulties in the numerical implementation of the boundary conditions. One example is the solution of Navier-Stokes equations in fluid mechanics. Another example is the flexural vibration analysis of a thin beam or a plate. Like some other numerical methods, the GDQM discretizes the spatial derivatives and, therefore, reduces the partial differential equations into a set of algebraic equations. To solve these equations, the boundary conditions have to be implemented appropriately. The details of the DQM and its applications can be found in [3] [9] -[16] . AL-SAIF and Zheng-You [17] presented improve to the traditional DQM by using the upwind difference scheme for the convective terms to solve the coupled two-dimensional incompressible Navier-stokes equations and heat equation. The results show that the new method is more accurate, and has better convergence than the conventional DQM for numerically computing the steady-state solution. AL-SAIF and Zheng-You [18] studied the two-dimensional steady flow of an incompressible second-order viscoelastic fluid between two parallel plates. By using the DQM with only a few grid points, the high-accurate numerical results were obtained.
The investigations of blood flow through arteries are of considerable importance in many cardiovascular diseases particularly atherosclerosis. Under normal conditions, blood flow in the human circulatory system depends upon the pumping action of the heart and this produces a pressure gradient throughout the arterial network. During recent years, the effect of magnetic field on the flow has been studied. MHD viscous flow though pipes plays significant role in different areas of science and technology such as Petroleum industry, Biomechanics, Drainage and Irrigation engineering and so on. The electromagnetic force (Lorentz force) acts on the blood and this force opposes the motion of blood and there by flow of blood is impeded, so that the external magnetic field can be used in the treatment of some kinds of diseases like cardiovascular diseases and in the diseases with accelerated blood circulation such as hemorrhages and hypertension. Earlier studies in flow in porous media have revealed the Darcy law which relates linearly the flow velocity to the pressure gradient across the porous medium. An important characteristic for the combination of the fluid and the porous medium is the tortuosity which represents the hindrance to flow diffusion imposed by local boundaries or local viscosity.
No slip boundary conditions are a convenient idealization of the behavior of viscous fluids near walls. The inadequacy of the no-slip condition is quite evident in polymer melts which often exhibit microscopic wall slip. The slip condition plays an important role in shear skin, spurt, and hysteresis effects. The boundary conditions relevant to flowing fluids are very important in predicting fluid flows in many applications. The fluids that exhibit boundary slip have important technological applications such as in polishing valves of artificial heart and internal cavities.
In situations like travel in vehicles, aircraft, operating jackhammer, and sudden movements of body during sports activities, the human body experiences external body acceleration. Prolonged exposure of a healthy human body to external acceleration may cause serious health problem like headache, increase in pulse rate and loss of vision on account of disturbances in blood flow.
Many mathematical models have already been investigated by several research workers to study the unsteady pulsatile blood flow through porous medium under the influence of periodic body acceleration in the presence of magnetic field with slip boundary condition numerically and analytically. El-Shehawey et al. [19] -[22] studied the effect of body acceleration in different situations. They studied the effect of MHD flow of blood under body acceleration and the Womersley problem for pulsatile flow of blood through a porous medium. The blood flow through porous medium under periodic body acceleration has been studied. The analytical solutions of all above cases are obtained by using Laplace and finite Hankel transforms. El-Shehawey et al. [23] studied the pulsatile flow through a porous medium under the influence of body acceleration. An analytical solution is obtained by using Laplace and finite Hankel transforms. El-Shahed [24] studied pulsatile flow of blood through a stenosed porous medium under the influence of periodic body acceleration. Analytical solution is obtained by using Laplace and finite Hankel transforms. El-Shehawey et al. [25] studied the slip effects on the peristaltic flow of a non-Newtonian Maxwellian fluid. The Navier-Stokes equations are solved by using a perturbation analysis. Sanyal and Debnath [26] presented a mathematical model for studying the effect of magnetic field on pulsatile blood flow through an inclined circular tube with periodic body acceleration. The analytical solution is obtained by using Finite Hankel and Laplace transforms. Das and Saha [27] studied the arterial MHD pulsatile blood flow through a stenosed porous medium with periodic body acceleration. An analytical solution is obtained using Finite Hankel and Laplace transforms. Sanyal and Biswas [28] studied the effect of uniform transverse magnetic field on its pulsatile motion through an axisymmetric tube by assuming blood as incompressible biviscous fluid. The problem is solved by Perturbation technique with small amplitude of pulsation. Mathur and Jain [29] studied the pulsatile flow of blood through stenosed arteries, including the effects of body acceleration and a magnetic field. An analytical solution is obtained by using Hankel and Laplace transforms. Misra et al. [30] presented a mathematical modeling of blood flow in porous vessel having double stenosis in the presence of an external magnetic. This model is consistent with the principles of ferro-hydrodynamics and magnetohydrodynamics. Eldesoky [31] presented a mathematical analysis of unsteady blood flow through parallel plate channel under the action of an applied constant transverse magnetic field. Eldesoky [32] studied the slip effects on the unsteady MHD pulsatile blood flow through porous medium in an artery under the influence of body acceleration. An analytical solution is obtained by applying the Laplace transform. Mohan et al. [33] investigated the effect of magnetic field on blood flow in cylindrical artery through porous medium. An analytical solution is obtained by applying Laplace transforms and Finite Hankel Transforms. Tzirtzilakis [34] studied a mathematical model of biomagnetic fluid dynamics (BFD) under the action of magnetic field. The numerical results are obtained using a Finite Differences technique based on a pressure-linked pseudotransient method on a collocated grid. Mokhtar et al. [35] study the unsteady motion of the magneto-hydrodynamic biviscosity fluid with heat and mass transfer through a uniform porous medium between two permeable parallel walls, taking into account pulsation of the pressure gradient. A numerical solution of governing equations is obtained using a matching technique of a Runge-Kutta-Merson method and Newton iteration in a shooting. Malekzadeh [36] studied the influence of a magnetic field on the skin friction factor of steady fully-developed laminar flow through a pipe. A numerical solution of the governing equations is obtained by applying Finite Difference scheme. Sankar and Lee [37] developed a computational model to analyze the effects of magnetic field in a pulsatile flow of blood through narrow arteries with mild stenosis. Finite Difference method is employed to solve the simplified nonlinear partial differential equation. Amira et al. [38] presented a mathematical model of Newtonian blood flow through the irregular stenosis to study the effect of body acceleration. The radial coordinate transformation is used to solve the governing equations and the numerical results are obtained by using Finite Difference method. Eldesoky et al. [39] studied the unsteady MHD pulsatile blood flow through porous medium under the influence of periodic body acceleration. A numerical solution of the equation of motion is obtained by applying a combination of a generalized differential quadrature method and 4th order Runge-Kutta method. Wang [40] presented exact solution of the Navier-Stokes equations of stagnation flows with slip.
In this paper, numerical solution using a new technique is applied to time dependent problem Navier-Stokes equations. Derivatives with respect to space variables are discretized using GDQM giving a system of ordinary differential equations for the time derivative, and time derivatives are discretized using 4th order RKM. A new technique gives a very good numerical solution for solving time dependent problems. Stability of 4th order RKM criteria is controlled with several values of time increment Δt and number of grid points N in space region. In this paper, GDQM used for studying the effect of slip condition on unsteady pulsatile blood flow through a porous medium under the influence of periodic body acceleration in the presence of magnetic field.
2. Mathematical Formulation
Consider the flow as shown in [32] , blood is supposed to be as an electrically conducting, Newtonian, incompressible, and viscous fluid in the presence of magnetic field in an axisymmetric cylindrical artery of radius R through porous medium with body acceleration. The fluid subjected to a constant magnetic field acts perpendicular to the artery. The slip boundary conditions are also taken into account. We assume that the magnetic Reynolds number of the flow is taken to be small enough, so that the induced magnetic and electric field can be neglected. We consider the flow as axially symmetric, pulsatile. The pressure gradient and body acceleration G are given by:
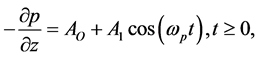 (1)
(1)
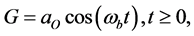 (2)
(2)
where AO and A1 are pressure gradient of steady flow and amplitude of oscillatory part respectively, aO is the amplitude of the body acceleration, 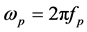 ,
, 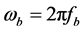 with fp is the pulse frequency, and fb is the body acceleration frequency and t is time.
with fp is the pulse frequency, and fb is the body acceleration frequency and t is time.
The governing equation of the motion for flow in cylindrical polar coordinates is given by
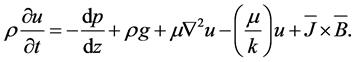 (3)
(3)
Maxwell’s equations are
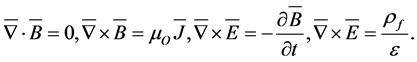 (4)
(4)
Ohm’s law is
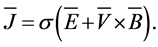 (5)
(5)
where 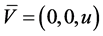 is the velocity distribution, ρ the blood density, μ the dynamic viscosity of the blood, μO magnetic permeability,
is the velocity distribution, ρ the blood density, μ the dynamic viscosity of the blood, μO magnetic permeability, 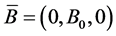 the magnetic field,
the magnetic field, 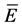 the electric field,
the electric field, 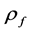 the volumetric free charge density,
the volumetric free charge density,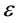 is the dielectric constant,
is the dielectric constant, 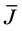 the current density, k is the permeability parameter of porous medium, and σ the electric conductivity of the blood. For small magnetic Reynolds number, the linearlized magnetohydrodynamic force
the current density, k is the permeability parameter of porous medium, and σ the electric conductivity of the blood. For small magnetic Reynolds number, the linearlized magnetohydrodynamic force 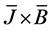 can be put into the following form:
can be put into the following form:
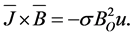 (6)
(6)
where 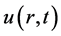 represents the axial velocity of the blood.
represents the axial velocity of the blood.
Under the above mentioned assumption, the equation of motion is:
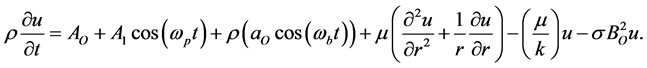 (7)
(7)
The boundary conditions that must be satisfied by the blood on the wall of artery are the slip conditions. For slip flow the blood still obeys the Navier-Stokes equation, but the no-slip condition is replaced by the slip condition 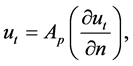 where ut is the tangential velocity, n is normal to the surface, and Ap is a coefficient close to the mean free path of the molecules of the blood [40] and then the boundary conditions on the wall of the artery are:
where ut is the tangential velocity, n is normal to the surface, and Ap is a coefficient close to the mean free path of the molecules of the blood [40] and then the boundary conditions on the wall of the artery are:
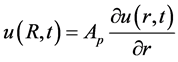 at
at 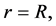
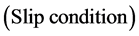 (8a)
(8a)
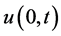 is finite at
is finite at 
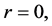 (8b)
(8b)
Let us introduce the following dimensionless quantities:
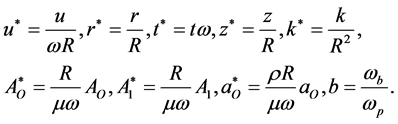 (9)
(9)
The Hartmann number, Ha, the Womersley parameter, α and the Knudsen number, kn are defined respectively by:
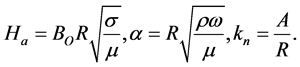 (10)
(10)
In terms of these variables, Equations (7) and (8) can be rewritten in the non-dimensional form after dropping the stars becomes:
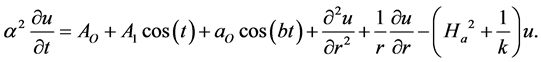 (11)
(11)
Also the boundary conditions are:
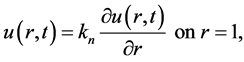 (12a)
(12a)
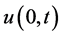 is finite (axis of the pipe) (12b)
is finite (axis of the pipe) (12b)
And the initial condition is:
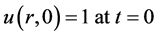 (12c)
(12c)
3. Generalized Differential Quadrature Method (GDQM)
The DQM is a numerical solution technique for initial and/or boundary value problems. This technique has been successfully employed in a variety of problems in engineering and physical sciences. The DQM approximates the derivative of a function at any location by a linear summation of all the functional values along a mesh (grid) line. The GDQM is systematically employed to solve problems in Fluid mechanics, Vibration analysis and Structural analysis. The technique of GDQM for the solution of partial differential equations extended and generalized. Numerical examples have shown the super accuracy, efficiency, convenience and the great potential of this method. A GDQM, which was recently proposed by Shu and Richards [7] [8] for solving partial differential equations in fluid mechanics. For the discretization of the first and higher order derivatives, the following linear constrained relationships are applied
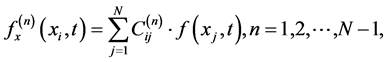 (13)
(13)
For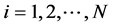 ; where
; where 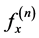 indicate nth order derivatives of
indicate nth order derivatives of 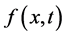 with respect to x at
with respect to x at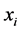 , N is the number of grid points in the whole dominant
, N is the number of grid points in the whole dominant 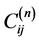 are the weighting coefficients. The key to DQ is to determine the weighting coefficients for the discretization of a derivative of any order. In order to find a simple algebraic expression for calculating the weighting coefficients without restricting the choice of grid meshes, Shu choose Lagrange interpolated polynomials as the tests functions. Shu and Richards [7] [8] gave a convenient and recurrent formula for determining the derivative weighting coefficients.
are the weighting coefficients. The key to DQ is to determine the weighting coefficients for the discretization of a derivative of any order. In order to find a simple algebraic expression for calculating the weighting coefficients without restricting the choice of grid meshes, Shu choose Lagrange interpolated polynomials as the tests functions. Shu and Richards [7] [8] gave a convenient and recurrent formula for determining the derivative weighting coefficients.
To determine the weighting coefficients of the GDQ method as:
Weighting coefficients for the first order derivative
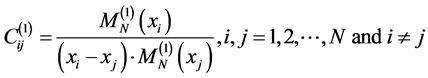 (14)
(14)
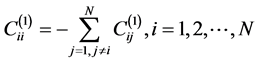 (15)
(15)
where
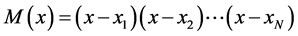 (16.1)
(16.1)
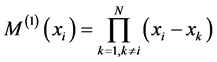 (16.2)
(16.2)
Weighting coefficients for the second and higher order derivatives
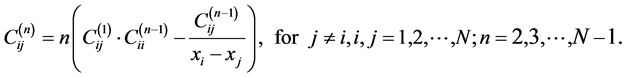 (17)
(17)
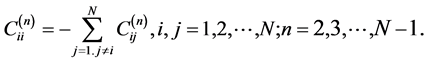 (18)
(18)
where 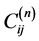 and
and 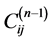 are the weighting coefficients of the nth and the (n−1)th derivatives. The
are the weighting coefficients of the nth and the (n−1)th derivatives. The 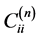 can be obtained from a relationship similar to Equation (15). Thus Equations (17) and (18) together with Equations (14) and (15) give a convenient and general form for determining the weighting coefficients for the derivatives of orders one through N – 1.
can be obtained from a relationship similar to Equation (15). Thus Equations (17) and (18) together with Equations (14) and (15) give a convenient and general form for determining the weighting coefficients for the derivatives of orders one through N – 1.
4. Numerical Discretization and Stability of the Scheme
In the present study, substituting the GDQ derivative approximations given in Equation (13) in the governing Equation (11). The coordinates of the grid points are chosen according to Chebyshev-Gauss-Lobatto by using N sampling as:

The GDQM is applied for the discretization of space derivatives of the unknown function u, we obtain the ordinary differential equation
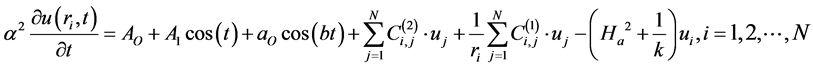 (19)
(19)
where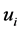 ,
, 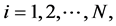 is the velocity value at the grid
is the velocity value at the grid 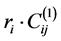 and
and 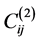 are the weighting coefficient matrixes of the first and second order derivatives.
are the weighting coefficient matrixes of the first and second order derivatives.
Similarly, the derivatives in the boundary conditions can be discretized by the GDQM. As a result, the numerical boundary conditions can be written as:
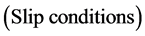
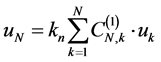 (20a)
(20a)
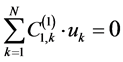 (20b)
(20b)
Equation (20) can’t be easily substituted into the governing equation. However, we can give solutions, 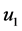 and
and 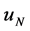 as:
as:
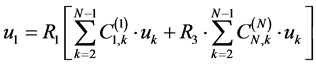 (21a)
(21a)
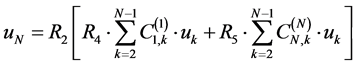 (21b)
(21b)
According to Equation (21), u1 and uN are expressed in terms of 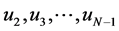 and can be easily substituted into the governing Equation (19). In total we have N unknowns
and can be easily substituted into the governing Equation (19). In total we have N unknowns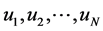 . In order to close the system, the discretized governing Equation (19) has to be applied at
. In order to close the system, the discretized governing Equation (19) has to be applied at ![]() mesh points. This can be done by applying Equation (19) at grid points
mesh points. This can be done by applying Equation (19) at grid points 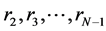 Substituting Equation (21) into Equation (19) gives:
Substituting Equation (21) into Equation (19) gives:
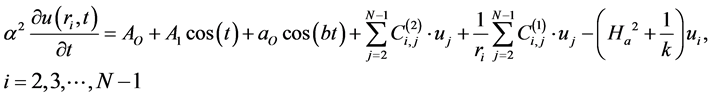 (22)
(22)
It is noted that Equation (22) has ![]() equations with
equations with ![]() unknowns.
unknowns.
Now, the discretization for time derivative will be performed by using Runge-Kutta Method. Now, 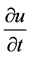 is also considered discretized as
is also considered discretized as 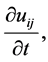 thus Equation (22) is a set of DQ algebraic equations which can be written in a matrix form
thus Equation (22) is a set of DQ algebraic equations which can be written in a matrix form
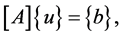 (23)
(23)
where 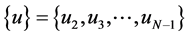 is a vector of unknown
is a vector of unknown ![]() functional values at all discretized points of the region, [A] is the
functional values at all discretized points of the region, [A] is the 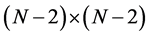 coefficient matrix, and the right hand side vector
coefficient matrix, and the right hand side vector 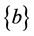 of size
of size 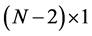 contains first order time derivatives of the function u at the same discretized points. Therefore a numerical scheme is necessary for handling these time derivatives. Equation (23) can be solved by several time integration schemes such as Euler, Modified Euler, and Runge-Kutta Methods. Here, Runge-Kutta Method is going to be used since it is a one step method obtained from the Taylor series expansion of u up to and including the terms involving
contains first order time derivatives of the function u at the same discretized points. Therefore a numerical scheme is necessary for handling these time derivatives. Equation (23) can be solved by several time integration schemes such as Euler, Modified Euler, and Runge-Kutta Methods. Here, Runge-Kutta Method is going to be used since it is a one step method obtained from the Taylor series expansion of u up to and including the terms involving 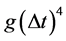 where
where ![]() is the step size with respect to time. The 4th order RKM since its stability region is larger comparing to the other time integration methods and simple for the computations.
is the step size with respect to time. The 4th order RKM since its stability region is larger comparing to the other time integration methods and simple for the computations.
The 4th order RKM is applied to discretized time derivatives in the resulting system of algebraic Equation (23). RKM is a one step method for solving initial value problems. Therefore the resulting algebraic system of Equation (23) can originally be considered as an initial value problem in the form (a set of ordinary differential equations in time)
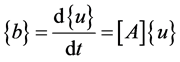 (24)
(24)
Thus the 4th order RKM gives for the governing equation the following vector equation
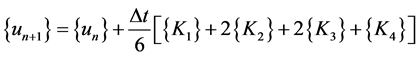 (25)
(25)
where;
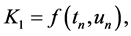
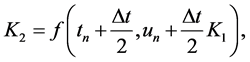
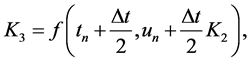
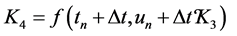
Applying 4th order RKM Equation (25) in Equation (24). Thus, we can easily write by taking 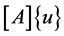 as the vector function
as the vector function 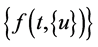 in the sample initial value problem
in the sample initial value problem 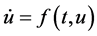 So,
So,
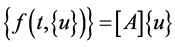 (26)
(26)
The Matlab program has been used to solve this problem and get the velocity distribution.
5. Numerical Results and Discussion
In this paper, numerical solution (Comparative Study) using a new technique is applied to study slip effect of unsteady MHD pulsatile flow through porous medium in an artery under the influence of periodic body acceleration using GDQM. A new technique gives a very good numerical solution for solving time dependent problems. The present approach of GDQM used the method of directly Substitutes the Boundary Conditions into the Governing Equations is referred to as (SBCGE); this method overcomes the drawbacks of the δ-technique in implementing the derivative conditions. The problem is reduced by using GDQM to a system of ODEs that is solved by the 4th order RKM. Numerical results of the problem is obtained and compared with available data in the literature and found that the present numerical schemes give better solutions.
A numerical code has been written to calculate the axial velocity according to Equation (23). In order to check our code and to discuss the stability and accuracy of the new technique, comparison the results with the exact solution [41] , we run it for the parameters related to a realistic physical problem similar to [41] . Figure 1, Figure 2 for steady MHD flow through a porous medium with constant pressure gradient, for instance, for Ao = 1, Ha = 1, k = 0.5, kn = 0.0, t = ∞ and r = 0.5, we obtain the axial velocity u = 0.12374654323755, which equals (if we keep 15 digits after the decimal point) to the result of [41] .
Also comparison the results of the new technique with [32] [39] [42] -[44] . Also comparison the results of the new technique with the analytical solution [45] , we run it for the parameters related to a realistic physical problem
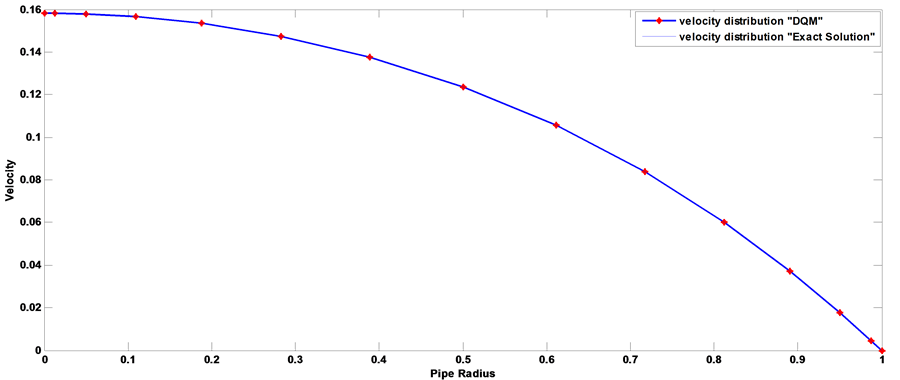
Figure 1. Comparisons between exact and numerical solution of velocity with the pipe radius [kn = 0, AO = 1, A1 = 0, aO = 0, b = 0, Ha = 1, k = 0.5, t→∞].
similar to [45] , for unsteady MHD pulsatile flow through porous medium in an artery under the effect of body acceleration, for instance, for α = 3, Ao = 2, A1 = 4, ao = 3, b = 2, Ha = 1, k = 0.5, kn = 0.0, t = 1 and r = 0.5, we obtain the axial velocity u = 0.60950 (if we keep five digits after the decimal point), which compared with the analytical solution [45] .
In this paper, Slip effects on the unsteady MHD pulsatile blood flow through porous medium in an artery under the influence of periodic body acceleration have been studied. Figures 2-10 show effects of slip condition on the axial velocity with time. Figures 2-4 show the relation between the axial velocity with time on the steady
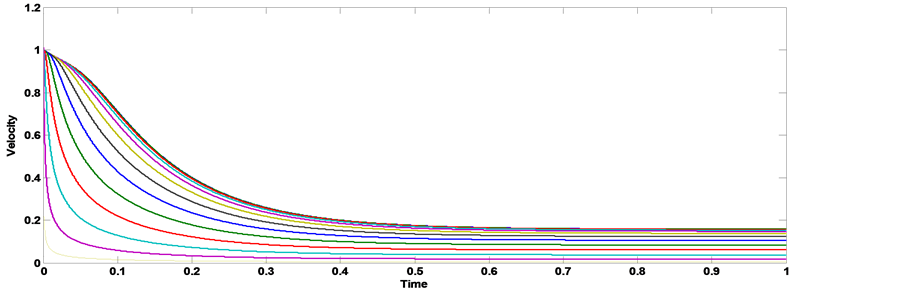
Figure 2. Comparisons between exact and numerical solution of velocity with the pipe radius [kn = 0, AO = 1, A1 = 0, aO = 0, b = 0, Ha = 1, k = 0.5, t→∞].
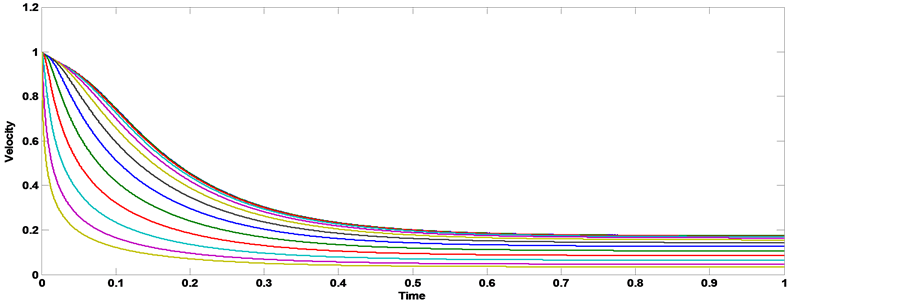
Figure 3. Comparisons between exact and numerical solution of velocity with the pipe radius [kn = 0.09, AO = 1, A1 = 0, aO = 0, b = 0, Ha = 1, k = 0.5, t→∞].
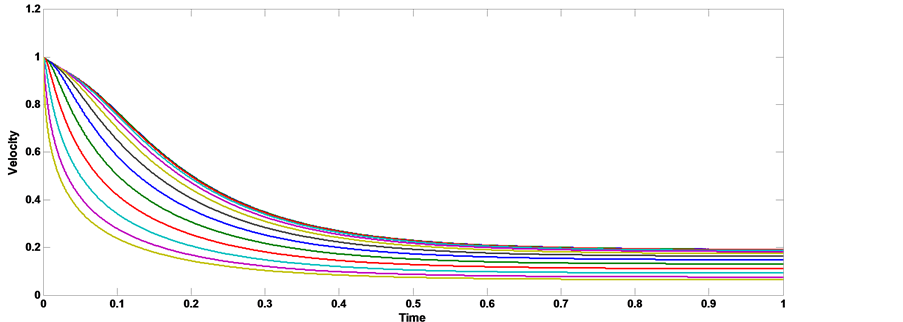
Figure 4. Comparisons between exact and numerical solution of velocity with the pipe radius [kn = 0.2, AO = 1, A1 = 0, aO = 0, b = 0, Ha = 1, k = 0.5, t→∞].
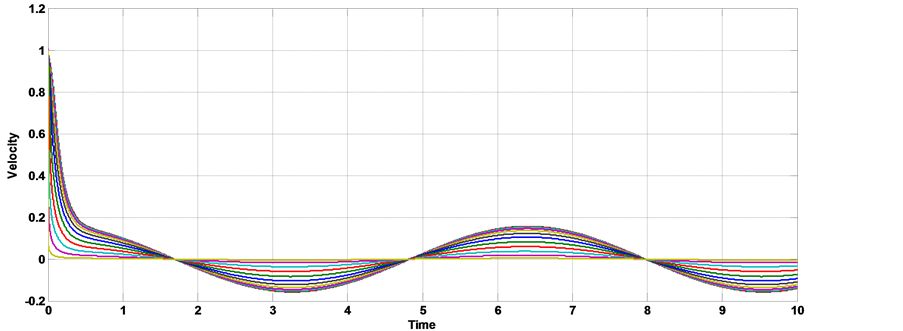
Figure 5. The velocity distribution with time [α = 1, kn = 0, AO = 1, A1 = 1, aO = 0, b = 0, Ha = 1, k = 0.5].
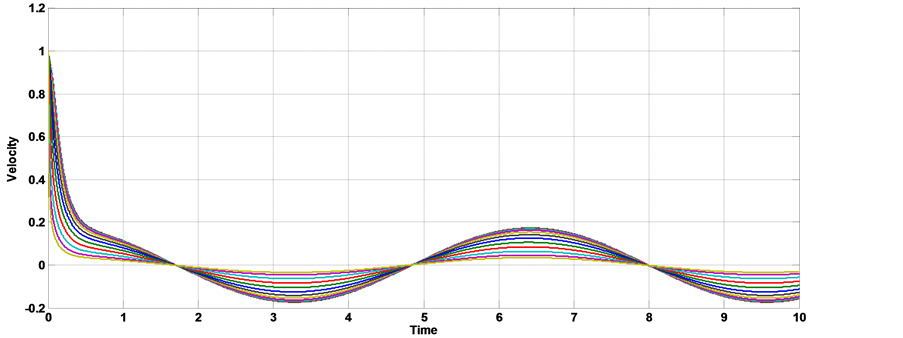
Figure 6. The velocity distribution with time [α = 1, kn = 0.09, AO = 1, A1 = 1, aO = 0, b = 0, Ha = 1, k = 0.5].
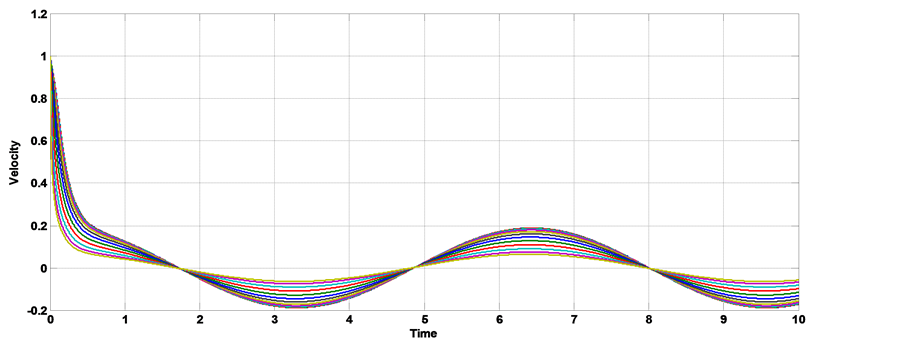
Figure 7. The velocity distribution with time [α = 1, kn = 0.2, AO = 1, A1 = 1, aO = 0, b = 0, Ha = 1, k = 0.5].
MHD blood flow through a porous medium with constant pressure gradient, we show from the figures that the presence of slip condition delay the time that the axial velocity need to reaches the steady state, when kn = 0.0, the axial velocity reaches to steady state at t = 0.45 sec., when kn = 0.09, the axial velocity reaches to steady state at t = 0.55 sec. and when kn = 0.2, The axial velocity reaches to steady state at t = 0.65 sec. Figures 5-7
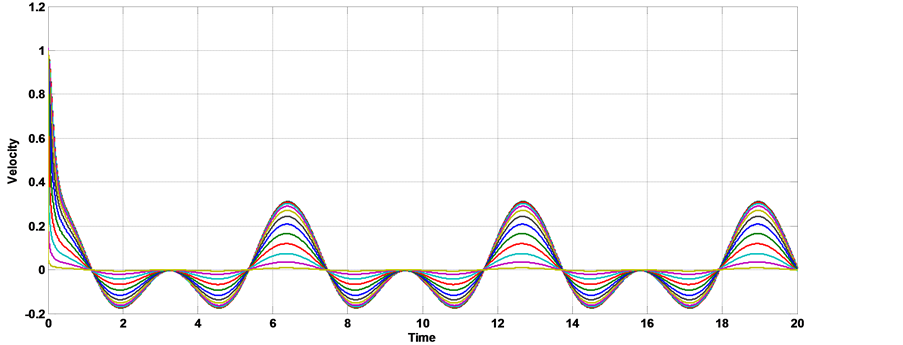
Figure 8. The velocity distribution with time [α = 1, kn = 0, AO = 1, A1 = 1, aO = 1, b = 2, Ha = 1, k = 0.5].
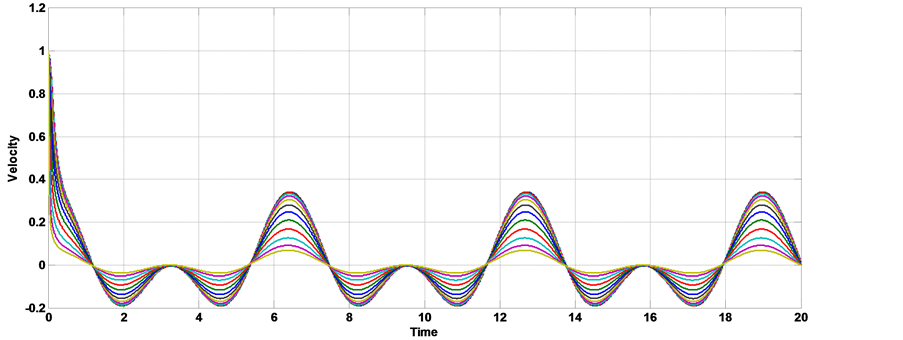
Figure 9. The velocity distribution with time [α = 1, kn = 0.09, AO = 1, A1 = 1, aO = 1, b = 2, Ha = 1, k = 0.5].
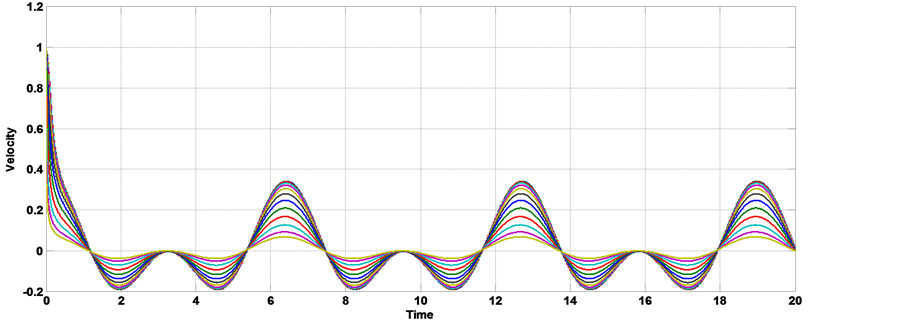
Figure 10. The velocity distribution with time [α = 1, kn = 0.2, AO = 1, A1 = 1, aO = 1, b = 2, Ha = 1, k = 0.5].
show the relation between the axial velocity with time on the unsteady MHD blood flow through a porous medium, we show from the figures that the presence of slip condition let to increase the amplitude of velocity oscillation at the peak. Figures 8-10 show the relation between the axial velocity with time on the unsteady MHD pulsatile blood flow through a porous medium under the effect of body acceleration, we show from the figures that the presence of slip condition let to increase the amplitude of velocity oscillation at the peak. Comparison between Figures 5-7 and Figures 8-10 to study the effect of body acceleration we note that the velocity profile in the presence of body acceleration make two peak down and one beak above and the magnitude of the velocity increase at the peak.
The axial velocity profile computed by using the velocity (23) for different values of Hartmann number Ha, Knudsen number kn, Womersley parameter α, frequency of body acceleration b, the parameter of porous medium k and have been shown through Figures 11-20. Thereby, we can be controlling the process of flow. It is observed from Figures 11, Figure 12, that as the Hartmann number increases the axial velocity of the blood decreases. Figure 13, Figure 14 show the effect of the Knudsen number on the axial velocity distribution, we note that the axial velocity of the blood increases with increasing Knudsen number. Figure 15, Figure 16 the axial velocity of the blood increases with increasing the permeability parameter of porous medium. Figure 17, Figure 18 the axial velocity of the blood decreases with increasing the frequency of body acceleration. Figure 19, Figure 20 the axial velocity of the blood increases with increasing Womersley parameter.
6. Conclusions
In this paper, a GDQM is presented to obtain numerical solutions of Navier-Stokes equations. The problem is reduced to a system of ODEs that is solved by fourth order Runge-Kutta method. Numerical results of the unsteady pulsatile blood flow through porous medium in the presence of magnetic field with periodic body acceleration and slip condition through a rigid straight circular tube (artery) have been studied. It is of interest to note
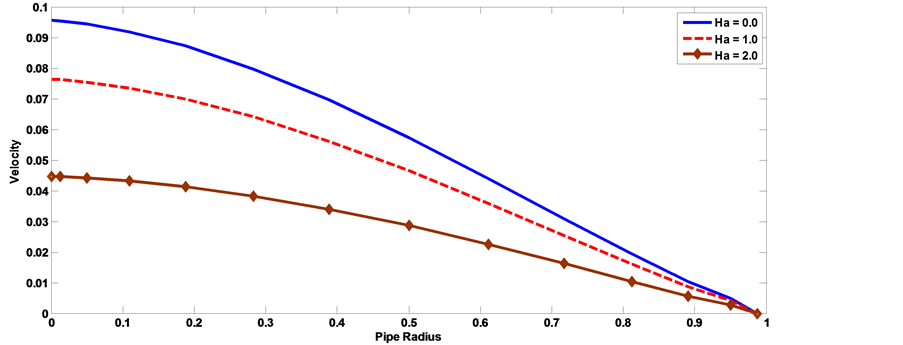
Figure 11. The effect of Hartman number on velocity distribution with the pipe radius [α = 1, kn = 0.02, AO = 1, A1 = 1, aO = 1, b = 2, k = 0.5, t = 1].
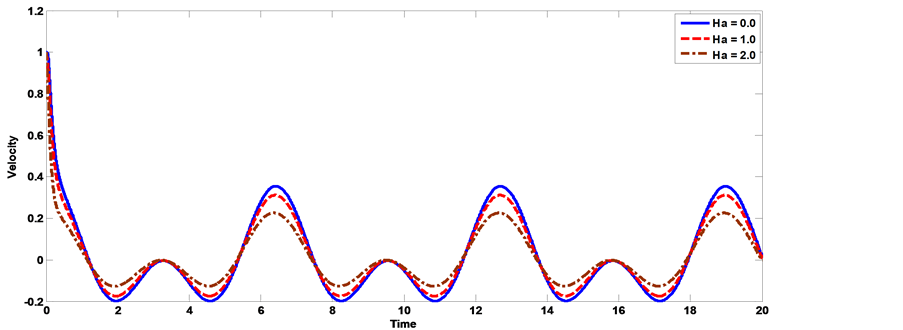
Figure 12. The effect of Hartman number on velocity distribution with time [α = 1, kn = 0.02, AO = 1, A1 = 1, aO = 1, b = 2, k = 0.5].
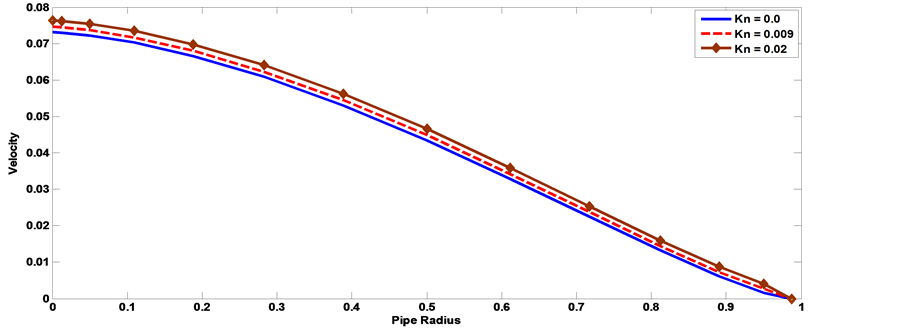
Figure 13. The effect of Knudsen number on velocity distribution with the pipe radius [α = 1, Ha = 1, AO = 1, A1 = 1, aO = 1, b = 2, k = 0.5, t = 1].
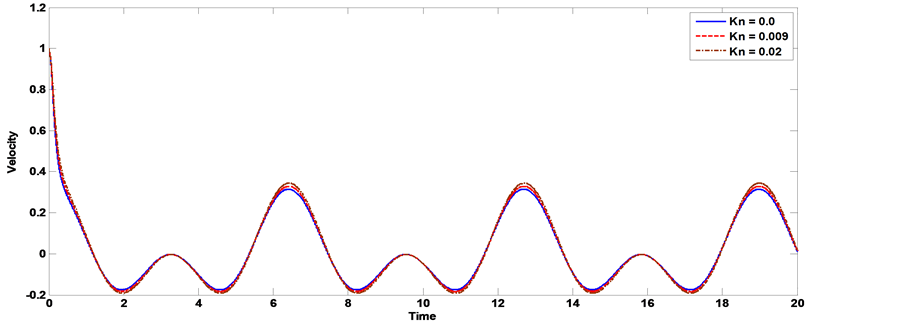
Figure 14. The effect of Knudsen number on velocity distribution with the pipe radius [α = 1, Ha = 1, AO = 1, A1 = 1, aO = 1, b = 2, k = 0.5, t = 1].
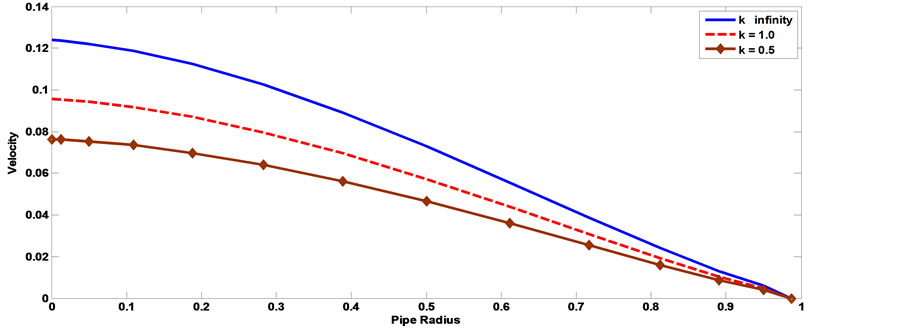
Figure 15. The effect of porosity number on velocity distribution with the pipe radius [α = 1, kn = 0.02, AO = 1, A1 = 1, aO = 1, b = 2, Ha = 1, t = 1].
that the axial velocity increases with increasing of the permeability parameter of porous medium, Womersley parameter and Knudsen number whereas it decreases with increasing the Hartmann number and frequency of body acceleration.
The present model gives a numerical solution of velocity distribution with pipe radius and time. It is of inter-
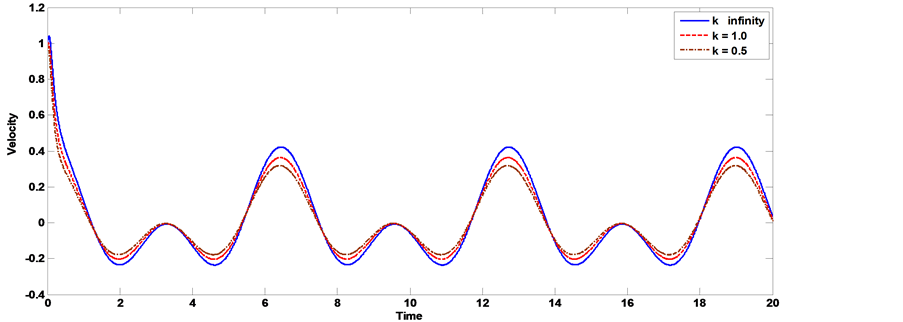
Figure 16. The effect of porosity number on velocity distribution with the pipe radius [α = 1, kn = 0.02, AO = 1, A1 = 1, aO = 1, b = 2, Ha = 1].
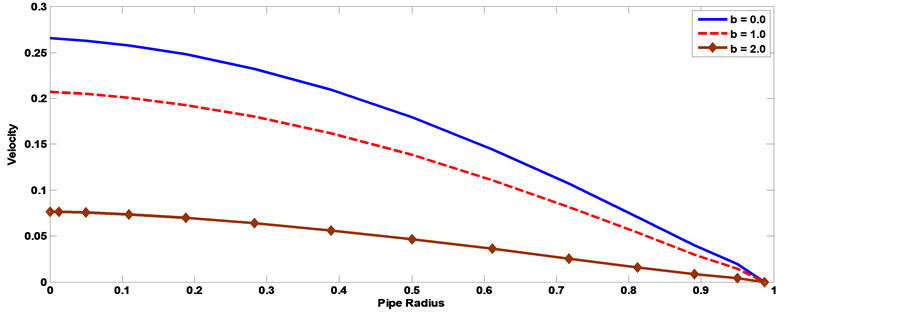
Figure 17. The effect of frequency of body acceleration on velocity distribution with the pipe radius [α = 1, kn = 0.02, AO = 1, A1 = 1, aO = 1, Ha = 1, k = 0.5 t = 1].
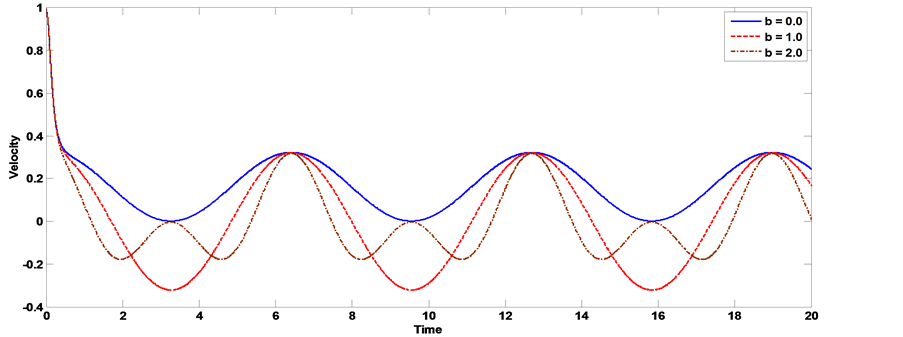
Figure 18. The effect of frequency of body acceleration on velocity distribution with time [α = 1, kn = 0.02, AO = 1, A1 = 1, aO = 1, Ha = 1, k = 0.5].
est to note that the result of the present model includes results of different mathematical models such as:
¾ The results of Eldesoky [32] have been recovered¾ The results of Eldesoky, Kamel, Reda, and Abumandour [39] have been recovered by taking Knudsen number kn = 0.0 (no slip condition),
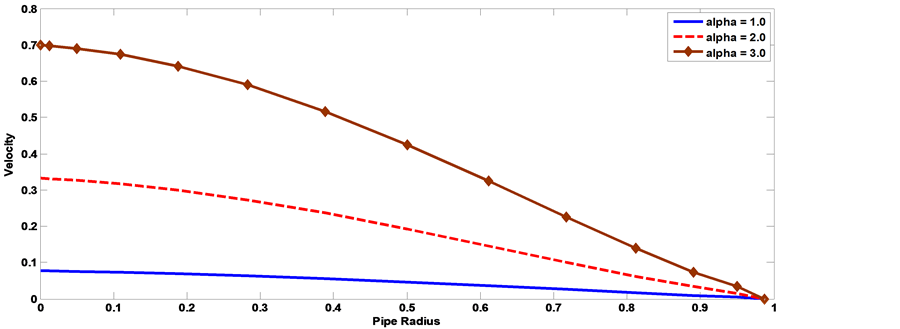
Figure 19. The effect of Womersley parameter on velocity distribution with the pipe radius [kn = 0.02, AO = 1, A1 = 1, aO = 1, b = 2, Ha = 1, k = 0.5, t = 1].
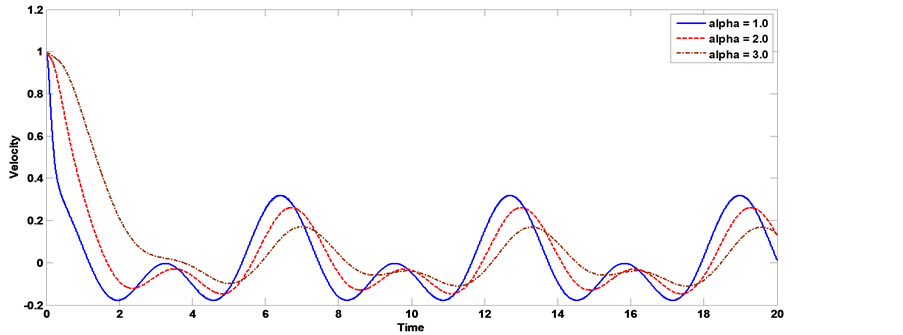
Figure 20. The effect of Womersley parameter velocity distribution with time [kn = 0.02, AO = 1, A1 = 1, aO = 1, b = 2, Ha = 1, k = 0.5].
¾ The results of Megahed et al. [45] , have been recovered by taking Knudsen number kn = 0.0 (no slip condition)¾ the results of Kamel and El-Tawil [43] have been recovered by taking Knudsen number kn = 0.0 (no slip condition), the permeability of porous medium k → ∞ without stochastic and nobody acceleration¾ The results of El-Shahed [44] have been recovered by taking Knudsen number kn = 0.0 (no slip condition) and Hartmann number Ha = 0.0 (no magnetic field)¾ The results of Chaturani and Palanisamy [42] have been recovered by taking Knudsen number kn = 0.0 (no slip condition), the permeability of porous medium k → ∞ and Hartmann number Ha = 0.0 (no magnetic field).
It is possible that a proper understanding of interactions of body acceleration with blood flow may lead to a therapeutic use of controlled body acceleration. It is therefore desirable to analyze the effects of different types of vibrations on different parts of the body. Such knowledge of body acceleration could be useful in the diagnosis and therapeutic treatment of some health problems (joint pain, vision loss, and vascular disorder), to better design of protective pads and machines.
By using an appropriate magnetic field it is possible to control blood pressure and also it is effective for conditions such as poor circulation, travel sickness, pain, headaches, muscle sprains, strains, and joint pains. The slip condition plays an important role in shear skin, spurt and hysteresis effects. The fluids that exhibit boundary slip have important technological applications such as in polishing valves of artificial heart and internal cavities.
Hoping that this investigation may have for further studies in the field of medical research, the application of magnetic field for the treatment of certain cardiovascular diseases, and also the results of this analysis can be applied to the pathological situations of blood flow in coronary arteries when fatty plaques of cholesterol and artery clogging blood clots are formed in the lumen of the coronary artery. The study is useful for evaluating the role of porosity when the body is subjected to magnetic resonance imaging (MRI).
References
- Bellman, R.E. and Casti, J. (1971) Differential Quadrature and Long-Term Integration. Journal of Mathematical Analysis and Applications, 34, 235-238. http://dx.doi.org/10.1016/0022-247X(71)90110-7
- Bellman, R.E., Kashef, B.G. and Casti, J. (1972) Differential Quadrature: A Technique for the Rapid Solution of Non-Linear Partial Differential Equations. Journal of computational Physics, 10, 40-52. http://dx.doi.org/10.1016/0021-9991(72)90089-7
- Shu, C. (2000) Differential Quadrature and Its Application in Engineering. Springer-Verlag, London. http://dx.doi.org/10.1007/978-1-4471-0407-0
- Quan, J.R. and Chang, C.T. (1989) New Insights in Solving Distributed System Equations by the Quadrature method-I, Analysis. Journal of Computers and Chemical Engineering, 13, 779-788. http://dx.doi.org/10.1016/0098-1354(89)85051-3
- Shu, C. and Richards, B. (1992) Application of Generalized Differential Quadrature to Solve Two-Dimensional Incompressible Navier-Stokes Equations. International Journal for Numerical Methods in Fluids, 15, 791-798. http://dx.doi.org/10.1002/fld.1650150704
- Wen, D. and Yu, Y. (1993) Calculation and Analysis of Weighting Coefficient Matrices in Differential Quadrature Method. Computational Engineering, Elsevier Oxford, 157-162.
- Shu, C. and Richards, B.E. (1990) High Resolution of Natural Convection in a Square Cavity by Generalized Differential Quadrature. Proceedings of 3rd International Conference on Advanced in numerical Methods in Engineering: Theory and Applications, Swansea, Vol. 2, 978-985.
- Shu, C. (1991) Generalized Differential-Integral Quadrature and Application to the Simulation of Incompressible Viscous Flows Including Parallel Computation. Ph.D. Thesis, University of Glasgow, Glasgow.
- Wen, D. and Yu, Y. (1993) Differential Quadrature Method for High Order Boundary Value Problems. Computational Engineering, 163-168.
- Tanaka, M. and Chen, W. (2001) Coupling Dual Reciprocity Boundary Element Method and Differential Quadrature Method for Time Dependent Diffusion Problems. Applied Mathematical Modelling, 25, 257-268. http://dx.doi.org/10.1016/S0307-904X(00)00052-4
- Pu, J.-P. and Zheng, J.-J. (2006) Structural Dynamic Responses Analysis Applying Differential Quadrature Method. Journal of Zhejiang University Science, 7, 1831-1838. http://dx.doi.org/10.1631/jzus.2006.A1831
- Zong, Z. and Zhang, Y.Y. (2009) Advanced Differential Quadrature Methods. Chapman & Hall/CRC Applied Mathematics and Nonlinear Science Series.
- Korkmaz, A., Aksoy, A.M. and Dag, I. (2011) Quartic B-Spline Differential Quadrature Method. International Journal of Nonlinear Science, 11, 403-411.
- Krowiak, A. (2008) Methods Based on the Differential Quadrature in Vibration Analysis of Plates. Journal of Theoretical and Applied Mechanics, 46, 123-139.
- Meral, G. (2013) Differential Quadrature Solution of Heat-and Mass-Transfer Equations. Applied Mathematical Modelling, 37, 4350-3459. http://dx.doi.org/10.1016/j.apm.2012.09.012
- Ramezani, M., Shahrezaee, M., Kharazi, H. and Kashany, L.H. (2012) Numerical Solutions of Differential Algebraic Equation by Differential Quadrature Method. Journal of Basic and Applied Scientific Research, 2, 11821-11828.
- Al-Saif, A.S.J. and Zhu, Z.Y. (2003) Application of Mixed Differential Quadrature Method for Solving the Coupled Two-Dimensional Incompressible Navier-Stokes Equation and Heat Equation. Journal of Shanghai University, 7, 343-351. http://dx.doi.org/10.1007/s11741-003-0007-x
- Al-Saif, A.S.J. and Zhu, Z.Y. (2006) Differential Quadrature Method for Steady Flow of an Incompressible Second-Order Viscoelastic Fluid and Heat Transfer Model. Journal of Shanghai University, 9, 298-306.
- Elshehawey, E.F., Elbarbary, E.M.E., Elsoud, A.S.N. and Elshahed, M. (1999) Blood Flow through a Porous Medium under Periodic Body Acceleration. Mathematical Sciences Research Hot-Line, 11, 27-31.
- Elshehawey, E.F., Elbarbary, E.M.E., Elsoud, A.S.N. and Elshahed, M. (1999) Womersley Problem for Pulsatile Flow of Blood through a Porous Medium. Proceedings of the 6th Conference on Theoretical and Applied Mechanics, Cairo, March 1999, 115-122.
- Elshehawey, E.F., Elbarbary, E.M.E., Afifi, N.A.S. and El-Shahed, M. (2001) MHD Flow of Blood under Body Acceleration. Integral Transforms and Special Functions, 12, 1-6. http://dx.doi.org/10.1080/10652460108819329
- El-Shehawey, E.F., Elbarbary, E.M.E., Afifi, N.A.S. and Elshahed, M. (2000) MHD Flow of an Elastico-Viscous Fluid under Periodic Body Acceleration. International Journal of Mathematics and Mathematical Sciences, 23, 795-799. http://dx.doi.org/10.1155/S0161171200002817
- Elshehawey, E.F., Elbarbary, E.M.E., Afifi, N.A.S. and El-Shahed, M. (2000) Pulsatile Flow of Blood through a Porous Mediumunder Periodic Body Acceleration. International Journal of Theoretical Physics, 39, 183-188. http://dx.doi.org/10.1023/A:1003611604207
- El-Shahed, M. (2003) Pulsatile Flow of Blood through a Stenosed Porous Medium under Periodic Body Acceleration. Applied Mathematics and Computation, 138, 479-488. http://dx.doi.org/10.1016/S0096-3003(02)00164-9
- El-Shehawy, E.F., El-Dabe, N.T. andEl-Desoky, I.M. (2006) Slip Effects on the Peristaltic Flow of a Non-Newtonian Maxwellian Fluid. Acta Mechanica, 186, 141-159. http://dx.doi.org/10.1007/s00707-006-0343-6
- Sanyal, D.C., Das, K. and Debnath, S. (2007) Effect of Magnetic Field on Pulsatile Blood Flow through an Inclined Circular Tube with Periodic Body Acceleration. Journal of Physical Science, 11, 43-56.
- Das, K. and Saha, G.C. (2009) Arterial MHD Pulsatile Flow of Blood under Periodic Body Acceleration. Bulletin of Society of Mathematicians Banja Luka, 16, 21-42.
- Sanyal, D.C. and Biswas, A. (2010) Pulsatile Motion through an Axi-Symmetric Artery in Presence of Magnetic Field. Assam University Journal of Science and Technology: Physical Science and Technology, 5, 12-20.
- Mathur, P. and Jain, S. (2011) Pulsatile Flow of Blood through a Stenosed Tube: Effect of Periodic Body Acceleration and a Magnetic Field. Journal of Biorheology, 25, 71-77. http://dx.doi.org/10.1007/s12573-011-0040-5
- Misra, J.C., Sinha, A. and Shit, G.C. (2011) Mathematical Modeling of Blood Flow in a Porous Vessel Having Double Stenoses in the Presence of an External Magnetic Field. International Journal of Biomathematics, 4, 207-225. http://dx.doi.org/10.1142/S1793524511001428
- Eldesoky, I.M. (2012) Mathematical Analysis of Unsteady MHD Blood Flow through Parallel Plate Channel with Heat Source. World Journal of Mechanics, 2, 131-137. http://www.SciRP.org/journal/wjm.
- Eldesoky, I.M. (2010) Slip Effects on the Unsteady MHD Pulsatile Blood Flow through Porous Medium in an Artery under the Effect of Body Acceleration. International Journal of Mathematics and Mathematical Sciences, 2012, Article ID 860239. http://dx.doi.org/10.1155/2012/860239
- Mohan, V., Prasad, V., Varshney, N.K. and Gupta, P.K. (2013) Effect of Magnetic Field on Blood Flow (Elastico-Viscous) Under Periodic Body Acceleration in Porous Medium. IOSR Journal of Mathematics, 6, 43-48.http://dx.doi.org/10.9790/5728-0644348
- Tzirtzilakis, E.E. (2005) A Mathematical Model for Blood Flow in Magnetic Field. Physics of Fluids, 17, Article ID: 077103.
- Abdelnaby, M.A., Eldabe, N.T.M. and Abouzeid, M.Y. (2006) Numerical Study of Pulsatile MHD Non-Newtonian Fluid Flow with Heat and Mass Transfer through a Porous Medium between Two Permeable Parallel Plates. Jour. Mech. Cont. & Math. Sci., 1, 1-15.
- Malekzadeh, A., Heydarinasab, A. and Dabir, B. (2011) Magnetic Field Effect on Fluid Flow Characteristics in a Pipe for Laminar Flow. Journal of Mechanical Science and Technology, 25, 333-339.
- Sankar, D.S. and Lee, U. (2011) FDM Analysis for MHD Flow of a Non-Newtonian Fluid for Blood Flow in Stenosed Arteries. Journal of Mechanical Science and Technology, 25, 2573-2581.http://dx.doi.org/10.1007/s12206-011-0728-x
- Amira, H.T., Ilyani, A. and Izzati, C.M.S.S.N. (2012) Effects of Body Acceleration on the Blood Flow through Irregular Stenosis. UMT 11th International Annual Symposium on Sustainability Science and Management, Terengganu, 9-11 July 2012, 735-744.
- Eldesoky, I.M., Kamel, M.H., Hussien, R.M. and Abumandour, R.M. (2013) Numerical Study of Unsteady MHD Pulsatile Flow through Porous Medium in an Artery Using Generalized Differential Quadrature Method (GDQM). International Journal of Materials, Mechanics and Manufacturing, 1, 200-206.
- Wang, C.Y. (2003) Stagnation Flows with Slip: Exact Solutions of the Navier-Stokes Equations. Zeitschrift fur Angewandte Mathematik und Physik, 54, 184-189. http://dx.doi.org/10.1007/PL00012632
- Megahed, A.A. and Kamel, M.H. (1988) Unsteady Motion of a Conducting Fluid through a Porous Medium in a Circular Pipe with Heat Transfer. Proceedings of 5th International Conference of Multiphase Transfer Phenomena, Miami, 1988.
- Chaturani, P. and Palanisamy, V. (1991) Pulsatile Flow of Blood with Periodic Body Acceleration. International Journal of Engineering Science, 29, 113-121. http://dx.doi.org/10.1016/0020-7225(91)90081-D
- Kamel, M.H. and El-Tawil, M.A. (2001) Stochastic Blood Flow through an Overlapping Arterial Stenosis. Journal of Engineering and Applied Science, 48, 623-635.
- El-Shahed, M. (2003) Pulsatile Flow of Blood through a Stenosed Porous Medium under Periodic Body Acceleration. Applied Mathematics and Computation, 138, 479-488. http://dx.doi.org/10.1016/S0096-3003(02)00164-9
- Megahed, A.A., Maher, B.M. and Eldesoky, I.M. (2004) Unsteady MHD Pulsatile Flow through Porous Medium in an Infinite Circular Pipe under the Effect of the Body Acceleration. Scientific Bulletin of the Faculty of Engineering, Ain Shams University, 39, 715-735.
NOTES

*Corresponding author.

