Advances in Materials Physics and Chemistry
Vol.3 No.1(2013), Article ID:29287,9 pages DOI:10.4236/ampc.2013.31010
Synthesis and Analysis of PZT Using Impedance Method of Reactance Estimation
1Department of Intelligent Mechanical Engineering, Faculty of Engineering, Fukuoka Institute of Technology, Fukuoka, Japan
2Faculty of Engineering, Ramkhamhaeng University, Bangkok, Thailand
Email: kswitsar@kmitl.ac.th, murayama@fit.ac.jp, lerdlekha@eng.ru.ac.th
Received January 28, 2013; revised February 16, 2013; accepted February 25, 2013
Keywords: BVD; Capacitance; Force; Frequency; Impedance; Inductance; PZT; Temperature
ABSTRACT
This study presents an analysis of equivalent circuit namely Butterworth Van Dyke (BVD) [1,2] by using impedance method to stimulate Zirconate Titanate (Piezoelectric ceramic) which is initially synthesized from Lead Oxide (PbO), Zirconium Dioxide (ZrO2) and Titanium Dioxide (TiO2) and vibrated in thickness mode. The reactance was estimated in the frequency range lower than the resonance frequency and then compared to the impedance obtained from measurement using impedance analysis machine model HP4192A and HP4194 [3]. The results from HP4194 were analyzed for BVD parameters: Motional resistance (R1), Inductor (L1), Capacitor (C1), and Capacitor corresponds to the electrostatic capacitance (Co). Another accuracy analysis was compared by the calculation results using the method of IEEE 176-1987 [4] to the impedance values measured by HP4192A. In this study, there were two conditions for experiment and consideration of parameter variation in BVD equivalent circuit: variation of temperature and mechanical force. These parameters are evaluated to design the efficient circuit for PZT utilization to obtain the optimal efficiency.
1. Introduction
Electronic circuit using BVD analysis for effectively stimulating PZT can be designed by adopting, for example, IEEE Standard [4,5], Smits [6], Sherrit [7], and Xu [8]. Smith’s method and Sherrit’s method would consider those parameters as complex numbers. Xu’s method would be similar to Smith’s method which considers the impedance of piezoelectric measured at the frequency values ranging from resonance frequency (fr) and antiresonance frequency (fa) as well as under mechanical force i.e. elastic, piezoelectric constant and coupling coefficient. In this study, five pieces of PZT, namely O01, N01, N02, N03, and N04, were synthesized from ratio of PbO:ZrO2:TiO2 (100:52:48) and burned at 700˚C for 1 hour [9,10] in order to experiment the density (r), PZT constant (d33), dielectric constant (K) at 1 kHz, electromechanical coupling coefficient (kt) and mechanical quality factor (Qm). In addition, the PZT were utilized in an ultrasonic cleaner.
2. Theory and Fundamental Method
2.1. Equivalent Circuit of BVD
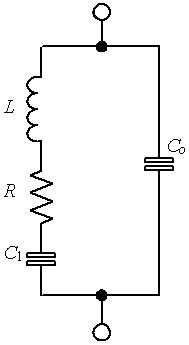
Electrical characteristics in thickness mode of PZT [3] tested in this study were comparable to the BVD equivalent circuit, which consists of R1 connected serially to C1
and L1 then all parallelly connected to Co [1,2,11] as shown in Figure 1(a). The resistance, the capacitance, and the inductance were comparable to the force friction (h), spring constant (k), and mass, respectively as shown in Figure 1(b).
Assuming R1, C1, L1, and Co were constants and independent on frequency and impedance [5] as given in Equation (1), the impedance equation at PZT resonance frequency (Zr), fr and fa, in terms of BVD relating parameters was obtained. In Figure 2, the impedance responding to fr and fa of PZT is shown.
 (a)
(a)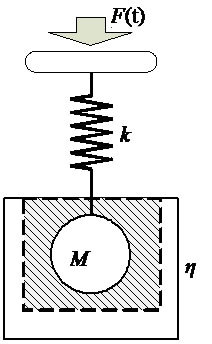 (b)
(b)
Figure 1. Equivalent circuit of PZT compared to mechanical characteristics: (a) The BVD model; (b) Mechanical model.
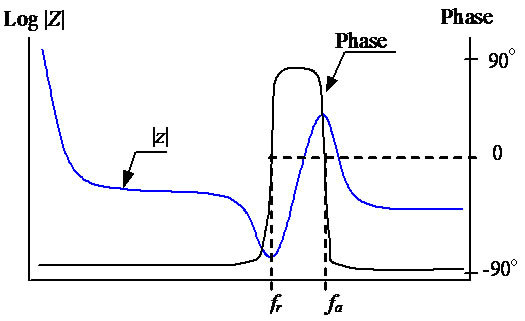
Figure 2. Frequency response characteristic of piezoelectric ceramic.
 (1)
(1)
The calculation of BVD circuit using impedance method by the capacitor ratio (r) is as shown in Equation (2), where wa is the angular velocity of the anti-resonance frequency (2pfa) and wr is the angular velocity of the resonance frequency (2pfr).
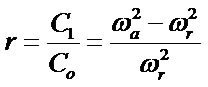 (2)
(2)
The reactance values of C1 and L1 in BVD circuit at low frequency range was observed. It was noted that the reactance of PZT was performed as a capacitor as shown in Equation (3).
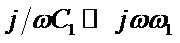 (3)
(3)
Therefore,
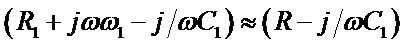 (4)
(4)
Then the impedance equation of PZT can be revised as shown in Equation (5).
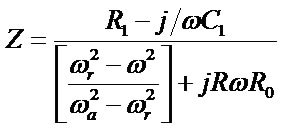 (5)
(5)
C1 can be calculated as given in Equation (6) by choosing the impedance measured at low frequency range where w is the angular velocity of the selected frequency and R is |Z| measured at resonance frequency.
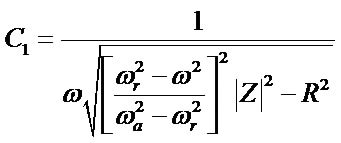 (6)
(6)
2.2. Measurement of Dielectric Constant (K)
Measurement of K or relative permittivity (er) of PZT is to test for the electrical characteristics which can be calculated by using Equation (7), where Cf is the capacitance at 1 kHz, t is the thickness of PZT measured from both metal poles, A is the area of metal pole, and eo is the dielectric constant of vacuum. The dielectric constant can be varied depending on the temperature (T) of substance based on Curie-Weiss Law [12] where Tc is the temperature of PZT with zero polarization, and C is Curie constant (103 to 105) as given in Equation (8).
 (7)
(7)
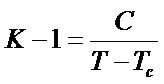 (8)
(8)
Equations (7) and (8) can also be revised as shown in Equation (9).
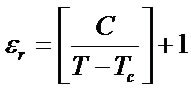 (9)
(9)
2.3. Measurement of PZT Constant (d33)
The value of d33, measured by Piezo-D meter model CADT (Channel Products Inc.), implies the ability to emit the electric charge of PZT when it is stimulated by mechanical force. Number 33 represents the three perpendicular directions of compression force on PZT.
2.4. Measurement of Electromechanical Coupling Coefficient (kt)
Electromechanical coupling coefficient (kt) represents the efficiency of transformation from electrical energy to mechanical force. In Equation (10), Δf is the difference between fr and fa.
 (10)
(10)
2.5. Measurement of Mechanical Quality Factor (Qm)
Qm represents the maximum ability of mechanical vibration in fr range where R1 is the impedance at resonance frequency as given in Equation (11).
 (11)
(11)
3. Analysis of BVD Equivalent Circuit
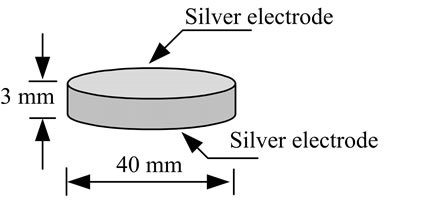
The PZT with 40 mm of diameter and 3 mm of thickness is electrode by silver paste at the top and the bottom as shown in Figure 3, and then connected to the system as
 (a)
(a) (b)
(b)
Figure 3. Physical of PZT sample: (a) Dimension of PZT; (b) Top view.
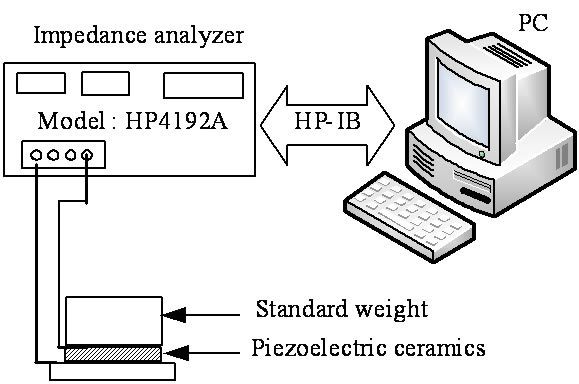
shown in Figure 4. The HP Vee program is applied to control the impedance analyzer model HP4192A via HP-IB interface and collect the impedance at 100 Hz to 1.3 MHz [4]. Then, the resonance frequency and the impedance at resonance frequency and lower resonance frequency will be applied to calculate R, L, and Co. The calculated value will be evaluated and compared with the value calculated by using Equation (1). In this paper, only the fundamental resonance is considered regardless the resonance frequency at harmonic period.
From experiment and measurement of PZT impedance, the calculated parameters from BVD model are as shown in Table 1. Figures 5 and 6 are illustrated the comparison of size (|Z|m) and phase of the impedance at 100 Hz to 100 kHz measured by impedance analyzer model HP4192A and the calculated impedance (|Z|cal and Phase Cal). The impedance at 1 kHz is selected to calculate in Equation (6). To obtain the appropriate value of C, the impedance at lower resonance frequency is suggested such as 100 Hz, 1 kHz, 2 kHz, 3 kHz, 6 kHz, and 14 kHz. The BVD parameters are as shown in Table 2 and the percentage of error is shown in Figure 7.
4. Experiment of PZT under Temperature Control
Physical characteristics of PZT were experimented by considering r, PZT constant (d33), kt, and Qm of electrical charge at 1 kHz. In this study, only the results from N01 and N04 (details are given in Table 3) were compared under room and controlled temperatures. Figure 8 shows
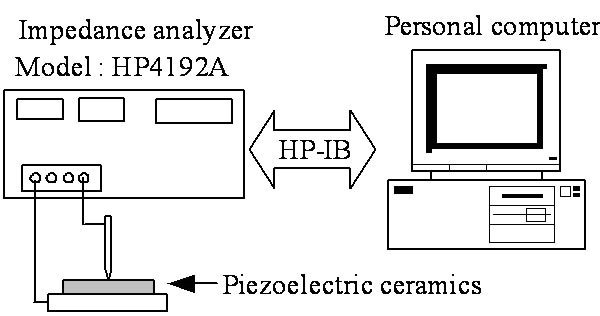
Figure 4. Impedance of PZT measurement diagram.

Figure 5. Gain impedance of PZT measurement at various frequency.
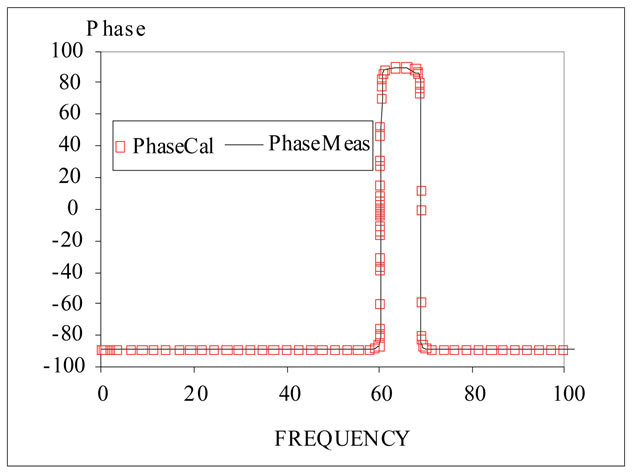
Figure 6. Phase impedance of PZT at various frequency.
the PZT experimental system connected with impedance analysis model HP4192A under temperature conditions.
Measuring the PZT impedance under room temperature was for assessing the influences of temperature on PZT impedance and comparing the results under room temperature and controlled temperature at various frequency. Figures 9 and 10 illustrate the PZT impedance
Table 1. The PZT properties.
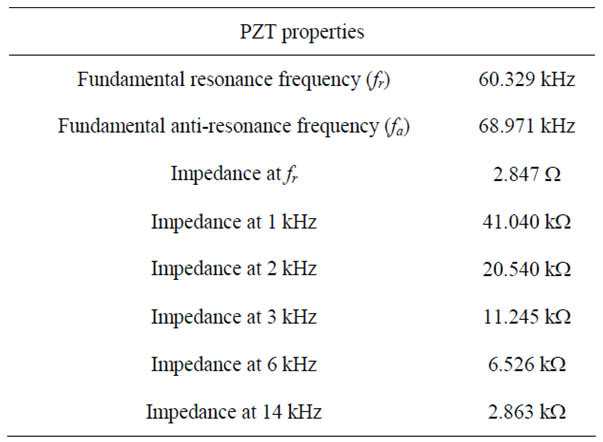
Table 2. Calculated parameters of BVD circuit at 100 Hz, 1 kHz, 2 kHz, 3 kHz, 6 kHz, and 14 kHz.
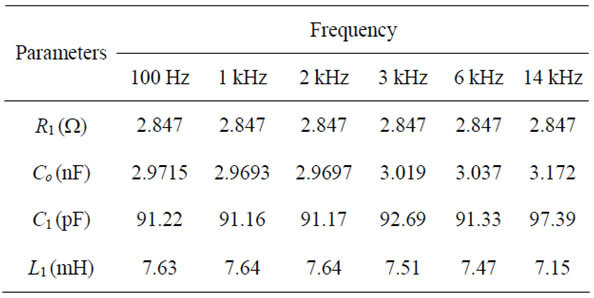
Table 3. Physical and electrical characteristics of PZT (N01 and N04).

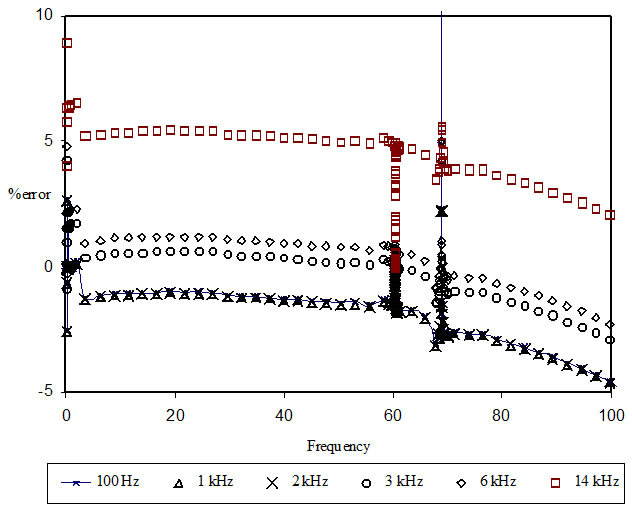
Figure 7. Error percentage of calculated impedance at various frequency.
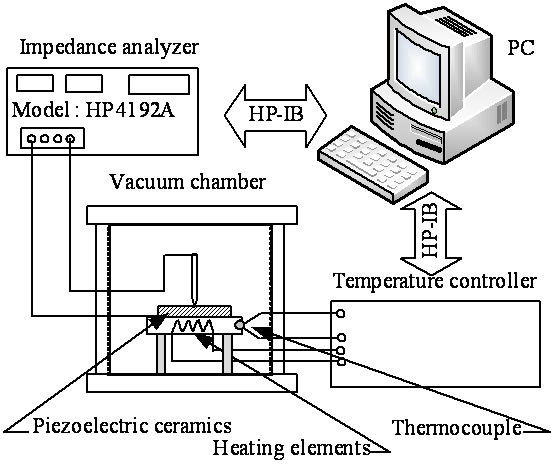
Figure 8. PZT experimental system and impedance analysis model HP4192A.
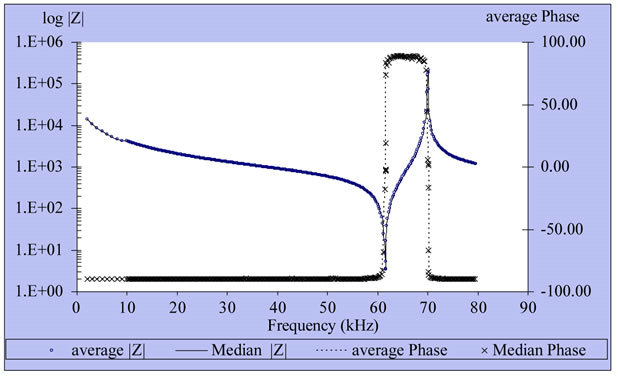
Figure 9. Impedance and phase at the frequency ranging from 100 Hz to 80 kHz of N01.
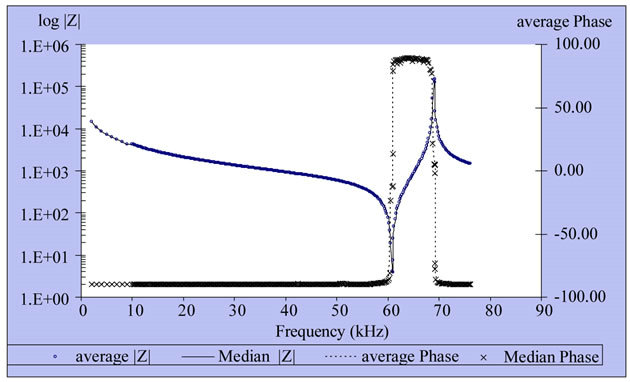
Figure 10. Impedance and phase at the frequency ranging from 100 Hz to 80 kHz of N04.
of N01 and N04 repeatedly measured 5 times by impedance analysis model HP4192A under room temperature at the frequency of 1 kHz to 80 kHz.
PZT was experimented by placing on heater plate in vacuum chamber under controlled temperature. The temperature can be controlled by a program developed on HP Vee via HP-IB port as shown in Figure 11. The temperature was varied from 25˚C to 230˚C with 20˚C

Figure 11. Position of PZT in temperature controlling chamber.
interval of measurement and the frequency was varied from 2 kHz to 80 kHz. Uncertainty of measurement and PZT was estimated by repeating 3 times of measurement.
4.1. Experimental Results under Temperature Conditions
The impedance of PZT in temperature controlled chamber (only N01) under specific temperature was similar to that under room temperature. However, it was observed that fr and fa were drifted. At 230˚C, fr increased about »1.6 kHz while fa decreased about »1 kHz. Therefore, the difference between fr and fa decreased about 2.6 kHz as shown in Figure 12. Moreover, when the temperature was increasing, the impedance at fr was also increasing up until 190˚C and then starting to decrease as illustrated in Figure 13.
4.2. Analysis of Impedance Variation in the Range of 100 Hz to 10 kHz
Experiment of PZT in the range of 100 Hz to 10 kHz was to calculate the impedance of BVD circuit by repeatedly measuring 30 times. An average and standard deviation of impedance are given in Figures 14 and 15, respectively. It can be noted that the standard deviation would increase at low frequency range and decrease as the frequency is rising.
4.3. Calculation of BVD Circuit Using Impedance Method
To calculate BVD circuit, average experimental values of fr, fa, and Zr at selected frequency ranging from 0.1 kHz to 10 kHz were used and then BVD parameters were obtained. The results were ranged as follows: L1 » 0.16 mH to 0.2 mH, C1 » 0.018 nF to 0.040 nF, Co » 0.06 nF to 0.18 nF. However, R1 was uniform due to the identical impedance at fr as shown in Table 4.
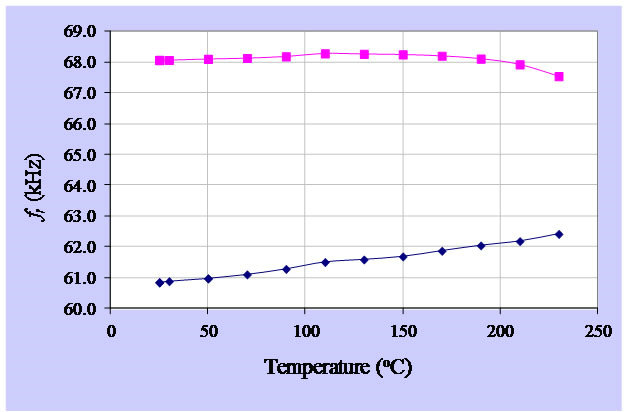
Figure 12. fr of PZT at various temperatures.
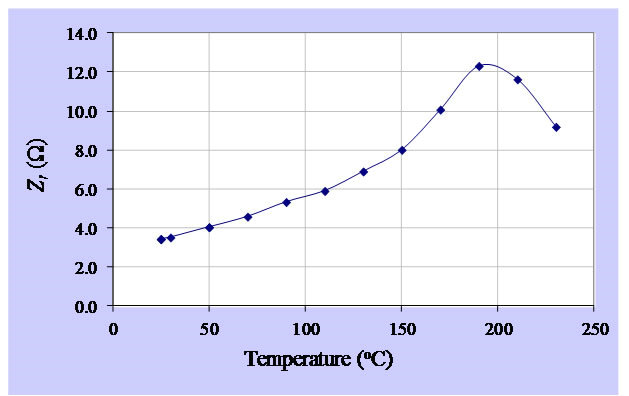
Figure 13. Impedance of PZT at fr at various temperatures.
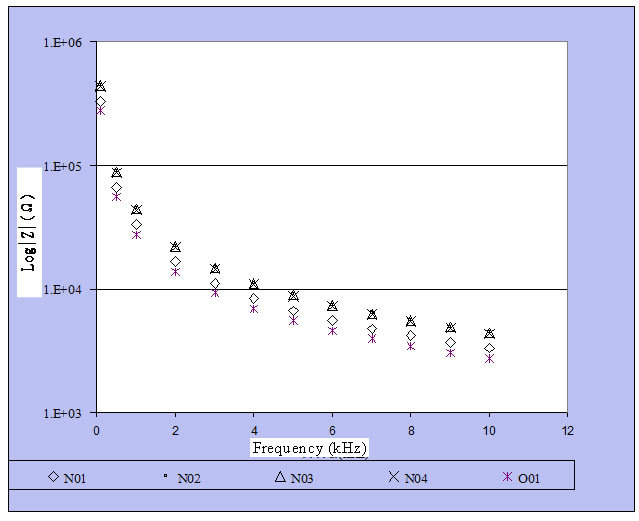
Figure 14. Average values at 100 Hz to 10 kHz of N01, N02, N03, N04, and O01.
4.4. Influences of Temperature Variation on BVD Parameters
When PZT was placed in the temperature controlling chamber at 23˚C, C1 would be decrease by 72% or 0.726%/˚C that leads to 255% of increase in L1. Therefore, the temperature would directly influence the char-
Table 4. BVD calculating parameters of N01 and N04 using impedance method.
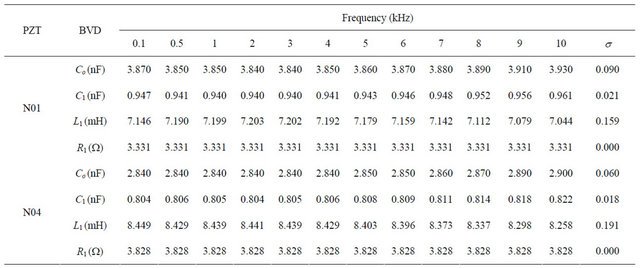
where s is the standard deviation.
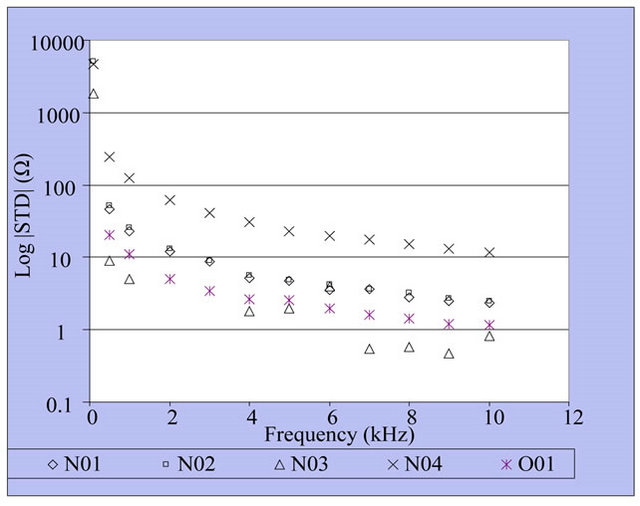
Figure 15. Standard deviation values at 100 Hz to 10 kHz of N01, N02, N03, N04, and O01.
acteristics of PZT as provided in Table 5.
5. Experiment of PZT under Mechanical Force
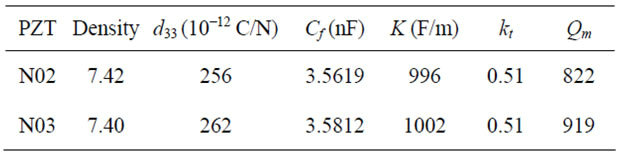
The parameters which was use in consideration of physical and electrical characteristics of PZT consists of r, d33, kt, and Qm at 1 kHz. In this case, comparison of N02 and N03 is as shown in Table 6.
Measurement of Zr under mechanical force was performed by using 0.5 lbs, 1.0 lbs, and 1.5 lbs of brass standard weights at room temperature. Each measurement was varied the frequency starting from 2 kHz to 80 kHz and repeated 30 times for calculating an average value. Figures 16(a) and (b) illustrate the experimental system and the brass standard weights, respectively.
Table 5. Percentage of BVD parameter changes as PZT temperature increasing by 230˚C.
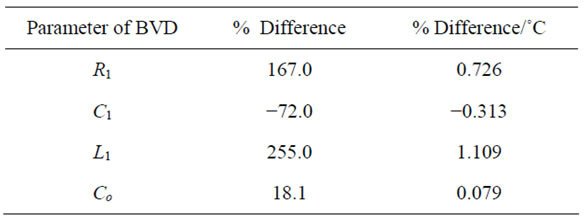
Table 6. Physical and electrical characteristics of PZT (N02 and N03).
5.1. Experiment of PZT at fr
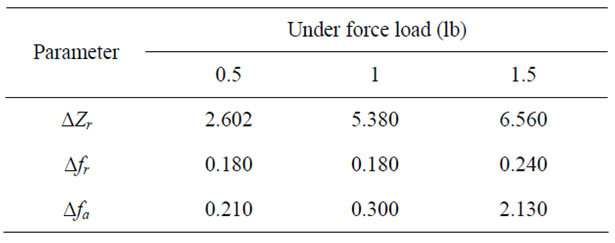
Standard weights (0.5 lbs, 1.0 lbs, and 1.5 lbs) were pressed to estimate fr, fa, and Zr as shown in Table 7 compared to weightless condition. The comparison was shown in Table 8. It can be noted that PZT pressed by 1.5 lbs standard weight would express higher fr and fa by »0.24 kHz and 2 kHz, respectively. However, Zr would be varied by the weight pressing and become stable at »6.5 W.
5.2. Experiment of Zr of PZT Connected Serially with Specific Capacitors
A capacitor (1.097 nF, 1.46 nF, 1.92 nF, 4.48 nF, 5.92 nF, 8.97 nF, and 33.016 nF) was connected serially with a given PZT (N02 and N03) and then, fr, fa, and Zr were
 (a)
(a)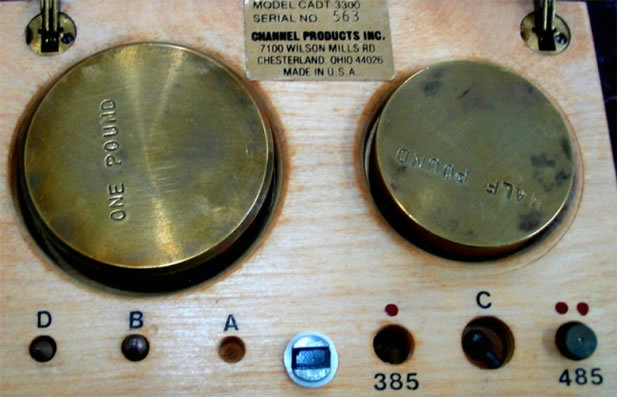 (b)
(b)
Figure 16. Impedance measurement using Impedance analysis model HP4192A and standard weight pressing: (a) System diagram; (b) Brass standard weights.
Table 7. fr, fa, and Zr of PZT under mechanical force loads.

Table 8. Variation of fr, fa, and Zr of PZT under mechanical force loads.
measured. The relationships of fs/2 (fsCL-fs) are as illustrated in Figures 17-20 where fs is the serial resonance frequency based on IEEE method [4,5]. The slope of linear relationship is 1/C1 as shown in Table 9.
5.3. Calculation of BVD Using Impedance Method
The average values of fr, fa, and Zr at resonance frequency obtained from experiments of N02 and N03 were used for analyzing BVD. By selecting the frequency ranging from 0.1 kHz to 10 kHz, it can be observed that
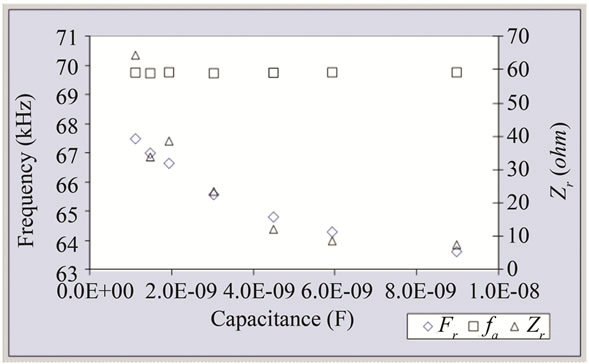
Figure 17. fr, fa, and Zr of N02 connected serially with various capacitors.

Figure 18. fs/2(fsCL-fs) of N02 connected serially with various capacitors.

Figure 19. fr, fa, and Zr of N03 connected serially with various capacitors.

Figure 20. fs/2(fsCL-fs) of N02 connected serially with various capacitors.
Table 9. Slopes of fs/2(fsCL-fs).

Co » 0.06 nF, C1 » 0.018 nF, L1 » 0.184 mH to 0.190 mH while R1 was identical due to the same impedance at fr as given in Table 10. The Table 11 shows the comparison of BVD parameters calculated by using impedance method, IEEE method, and HP4194 where IEEE method is the method of IEEE 176-1987, Δ1 is the percentage of difference between values obtained from impedance and IEEE 176-1987 method, and Δ2 is the percentage of difference between values obtained from impedance and HP4194 method.
5.4. Influences of Temperature on BVD Parameters under Mechanical Force
Variation of fr, fa, and Zr when PZT was pressed by standard weights was calculated for Co, C1, and L1 by impedance method. The differences are given in Table 12.
6. Conclusion
From calculation, it was observed that |Z| and Z(θ) of the impedance ranging from low frequency to fr and fa tended to be equal to the impedance measured by impedance analysis model HP4192A. Selecting low frequency range (100 Hz, 1 kHz, and 2 kHz) for calculating C would cause the error of |Z| by »−1%, On the other hand, selecting the impedance and frequency at 3 kHz the error would be exhibit less than 1%. However, the impedance and frequency at 14 kHz would exhibit the greater error by »5% because wL can much influence the impedance while 1/wL decreases. Therefore, the impedance selected for calculating should have the frequency lower than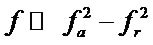 . Considering the percentage of impedance error, it can noted that the impedance at the frequency of 100 Hz, 1 kHz, and 2 kHz would provide the similar results with 20% - 25% of the maximum error of fa. From experiment of the calculated impedance, the accuracy of fr and fa was ±0.0033 kHz with the standard deviation of 0.00129 kHz which would be reliable for calculating BVD circuit. From experiment of accuracy which was compared between Zr of BVD equivalent circuit and Zr from measurement, it can be noted that Zr at fr of BVD circuit calculated by impedance method and IEEE 176-1987 would exhibit the error by »2.37% which was lower than HP4194 method (»4%). It would be because the impedance analysis using impedance analysis model HP4192A is applied the program to estimate fr more accurately. However, R1 was less different as it was a specific resistance at resonance frequency. Considering the influence of temperature on PZT characteristic, it was noted that the increase of temperature would contribute to less difference of fr and fa.
. Considering the percentage of impedance error, it can noted that the impedance at the frequency of 100 Hz, 1 kHz, and 2 kHz would provide the similar results with 20% - 25% of the maximum error of fa. From experiment of the calculated impedance, the accuracy of fr and fa was ±0.0033 kHz with the standard deviation of 0.00129 kHz which would be reliable for calculating BVD circuit. From experiment of accuracy which was compared between Zr of BVD equivalent circuit and Zr from measurement, it can be noted that Zr at fr of BVD circuit calculated by impedance method and IEEE 176-1987 would exhibit the error by »2.37% which was lower than HP4194 method (»4%). It would be because the impedance analysis using impedance analysis model HP4192A is applied the program to estimate fr more accurately. However, R1 was less different as it was a specific resistance at resonance frequency. Considering the influence of temperature on PZT characteristic, it was noted that the increase of temperature would contribute to less difference of fr and fa.
Table 10. Calculation of BVD parameters based on impedance method: a case of N02 and N03.
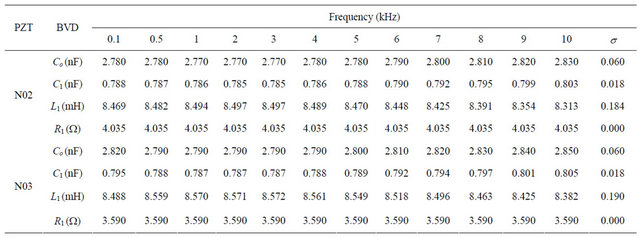
Table 11. Comparison of average BVD parameters from each method.

Table 12. Percentage of BVD parameter variation with 1.5 lbs standard weight pressing.

However, the increase of Zr would cause the variation of BVD calculated parameters such as decrease of C1, increase of R1, L1, and Co. On the other hand, the influences of mechanical force load on PZT parameters would cause fr, fa, and Zr increase that also contribute to R1 and C1 increase while L1 and Co decrease.
REFERENCES
- S. Sherrit, H. D. Wiederick and B. K. Mukherjee, “Accurate Equivalent Circuits for Unloaded Piezoelectric Resonators,” IEEE Ultrasonics Symposium Proceedings, Vol. 2, 1997, pp. 931-935.
- S. Sherrit, H. D. Wiederick, B. K. Mukherjee and M. Sayer, “An Accurate Equivalent Circuits for the Unloaded Piezoelectric Vibrator in the Thickness Mode,” Journal of Physics D: Applied Physics, Vol. 30, No. 16, 1997, pp. 2354-2363. doi:10.1088/0022-3727/30/16/014
- C. Jeerapan, W. Sriratana, P. Julsereewong and S. Kummool, “Analysis of Appropriate Parameters for Piezoelectric Ceramic Utilization by Using BVD Model,” ICCAS 2005, International Conference on Control, Automation and System, Gyeonggi-Do, 2-5 June 2005, pp. 2067-2070.
- “An American National Standard IEEE Standard on Piezoelectricity,” IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society, New York, 1988, ANSI/IEEE Std 176-1987.
- “Standard Definitions and Method of Measurement for Piezoelectric Vibrators,” The Institute of Electrical and Electronics Engineers Inc., New York, 1966, IEEE No. 177.
- J. G. Smits, “Iterative Method for Accurate Determination of Real and Imaginary Parts of the Materials Coefficients of Piezoelectric Ceramics,” IEEE Transactions on Sonics and Ultrasonics, Vol. 23, No. 6, 1976, pp. 393-402. doi:10.1109/T-SU.1976.30898
- S. Sherrit, H. D. Wiederick and B. K. Mukherjee, “NonIterative Evaluation of the Real and Imaginary Material Constants of Piezoelectric Resonators,” Ferroelectrics, Vol. 134, No. 1-4, 1992, pp. 111-119. doi:10.1080/00150199208015574
- Q. C. Xu, A. R. Ramachandran and R. E. Newnham, “Resonance Measuring Technique for Complex Coefficients of Piezoelectric Composites,” Journal of Wave-Material Interaction, Vol. 2, 1987, pp. 105-122.
- B. Jaffe, W. R. Cook Jr and H. Jaffe, “Piezoelectric Ceramics,” Journal of Sound and Vibration, Vol. 20, No. 4, 1972, pp. 562-563.
- T. Ikeda, “Fundamentals of Piezoelectricity,” 19th Edition, Oxford University Press, New York, 1990.
- S. Fujishima, K. Togawa and S. Ohta, “Analysis and Design of the Piezoelectric Ceramic Resonator Osillators,” 41st Annual Symposium on Frequency Control, Pennsylvania, 27-29 May 1987, pp. 391-397. doi:10.1109/FREQ.1987.201052
- M. Trainer, “Ferroelectrics and the Curie-Weiss Law,” European Journal of Physics, Vol. 21, No. 5, 2000, pp. 459-469. doi:10.1088/0143-0807/21/5/312

