Advances in Materials Physics and Chemistry
Vol.2 No.4(2012), Article ID:26026,8 pages DOI:10.4236/ampc.2012.24039
Electronic Structure of Gallium Phosphide Nanocrystals Core and (001)-(1 × 1) Oxidized Surface
1Ministry of Science and Technology, Baghdad, Iraq
2Department of Physics, College of Science, University of Baghdad, Baghdad, Iraq
Email: mudarahmed3@yahoo.com, Mohamed.Taqee@yahoo.com, raiedkamel@yahoo.com, thekra_alani@yahoo.com
Received September 21, 2012; revised October 25, 2012; accepted November 5, 2012
Keywords: Electronic Structure; GaP Nanocrystals; Oxidized Surface
ABSTRACT
The electronic structure of III-V zinc blend Gallium Phosphide nanocrystals is investigated using ab-initio density functional theory coupled with large unit cell for the core and surface parts. Two kinds of cells are investigated: multiple Bravais and multiple primitive cells. The results show that both energy gap and valence band width depend on the shape of the nanocrystal. Results also revealed that most electronic properties converge to some limit as the size of the large unit cell increases. Furthermore, the results have shown that the cohesive energy is decreasing with increasing size of nanocrystals. The core part is more degenerate, with larger energy gap and smaller valance and conduction bands than the surface.
1. Introduction
Gallium Phosphide is a compound semiconductor material with an indirect band gap of 2.2 eV at (300 K) [1,2]. It is zinc blend structured possess strong visible emission around 700 nm at room temperature and it is used in the manufacture of low-case red, orange and green light emitting diodes (LEDs) and semiconductor lasers can be made that emit in the visible spectrum, or even produce ultraviolet emission [3]. It has a relatively short life at higher current and its lifetime is sensitive to temperature. It is used standalone or together with GaAsP. The higher energy gap gives devices the ability to operate at higher temperatures, also used in power switching application semiconductor nanocrystals are tiny crystalline particles that exhibit size dependent optical and electronic properties. These particles also span the transition between small molecules and bulk crystal [4-6].
The large unit cell (LUC) method is used for the simulation of the band structure of semiconductor and other materials [7-11]. The multiples of Bravais and primitive cell will be used as the LUC. The two atom primitive cell is unacceptable central cell for LUC calculations since the interaction range (one Bravais lattice cell constant) is greater than the dimension of the primitive cell [12]. The aim of this research is to study the electronic structure of Gallium Phosphide nanocrystats core and oxidized surface.
2. Theory
The large unit cell (LUC) was used in the evaluation of the electronic structure of GaP nanocrystals using density functional theory (DFT). In this method, the number of atoms in the central cell (at k = 0) (k is the reciprocal lattice vector) is increased to match the real number of nanocrystal atoms. The large unit cell method is a supercell method that was suggested and first applied for the investigation of the electronic band structure of semiconductors [7-11]. This method differs from other supercell methods. Instead of adding additional k points to the reciprocal space, the number of atoms in the central cell (k = 0) is increased and a larger central unit cell is formed [7]. k = 0 is an essential part of the theory of LUC because it uses only one point in the reciprocal space that means only one cluster of atoms exist which is the features of quantum dots [13].
In the large unit cell method, only the lattice constant is optimized for the core part. However, the surface part bond lengths and angles still need to be optimized because of surface reconstruction. The oxidized surface contains the surface oxygen and outer four layers of GaP atoms whereas the core includes the remaining GaP atoms. The calculations were carried out for the core and surface geometries as shown in Figures 1 and 2.
Gaussian 03 program [14] is used to perform the core LUC and the oxygenated (001)-(1 × 1) surface that can be added to obtain a complete electronic structure view. The
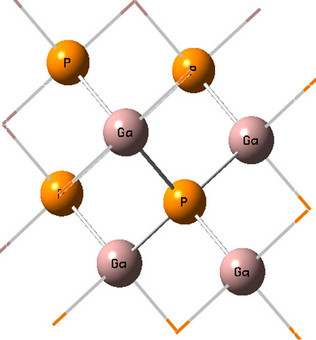
Figure 1. (Color online) GaP 8 atoms core LUC.

Figure 2. (Color online) Ga8P8O4 atoms oxidized surface LUC.
periodic boundary condition (PBC) method available in Gausssian 03 program is used to perform the present tasks [15]. Two multiple primitive parallelepiped cell cores 16 and 54 atoms and two multiple Bravais cubic cell cores 8 and 64 atoms are investigated as shown in Figures 3 and 4. The PBC utility are also used to calculate (001)-(1 × 1) GaP nanocrystal oxidized surface using slab geometry Ga8P8O4. Computational time and resources was the main obstacle in investigating bigger
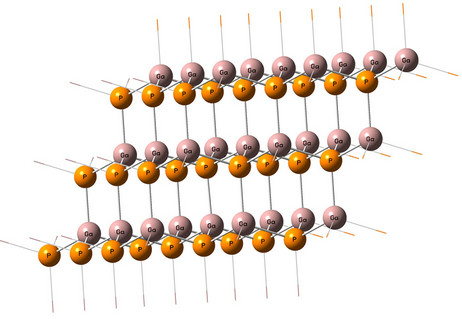
Figure 3. (Color online) GaP 54 atoms core LUC (parallelepiped shape primitive cell multiple).

Figure 4. (Color online) GaP 64 atoms core LUC (cubic Bravais cell multiple).
lattices or surfaces.
We shall use the density functional theory at the generalized gradient approximation (GGA) method level [16].
Kohn-Sham density theory [17-19] is widely used for self consistent—field electronic structure calculations of the ground state properties of atoms, molecules, and solids. In this theory, only exchange—correlation energy 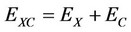 as a functional of the electron spin densities
as a functional of the electron spin densities 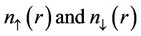 must be approximated.
must be approximated.
The local spin density (LSD) approximation:
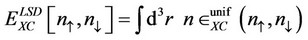 (1)
(1)
where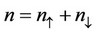 , and the generalized gradient approximation (GGA) [20-23]
, and the generalized gradient approximation (GGA) [20-23]
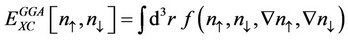 (2)
(2)
In comparison with LSD, GGA’s tend to improve total energy, atomization energies, energy barriers and structural energy differences.
To facilitate particle calculations,  and f must be parameterized analytic functions. The exchange correlation energy per particle of a uniform electron gas,
and f must be parameterized analytic functions. The exchange correlation energy per particle of a uniform electron gas, 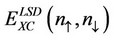 , is well established [24], but the best choice for
, is well established [24], but the best choice for 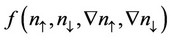 is still a matter of debate.
is still a matter of debate.
3. Calculations and Results
The nanocrystal core 3D periodic boundary condition (PBC) of GaP nanocrystalls calculations has been studied and using 2D (PBC) with particular regard to the oxygenated (001)-(1 × 1) surface is added to obtain a complete electronic structure view. Figure 5-6 shows the total energy as a function of the lattice constant optimization of 8 and 64 atom core LUC respectively. Figure 7 shows the total energy variation with lattice constant for 8 atoms of the surface part. These curves and similar curves for other LUCs are used to obtain equilibrium lattice constants for these cells. Figure 8 shows the variation of the energy gap with the variation of the number of core atoms, while the variation of both valance and conduction band widths with the variation of the number of core atoms are shown in Figure 9. Figure 10 displays the cohesive energy as a function of number of core atoms.
Density of states of core and surface LUC as a function of energy levels are shown in Figures 11 and 12. Figure 13 shows the atomic charge of oxidized Ga8P8O4 surface as a function of layer depth using the slap geometry method.
4. Discussion
In order to obtain equilibrium lattice constant, the total energy of 8 and 64 GaP atoms nanocrystal core is used, and the obtained results are shown in Figure 5-6. The results show that the minimum at the bottom represents the equilibrium lattice constant of this cell, while the equilibrium lattice constant occurred at a point in which the attraction forces between the atoms equals to the repulsion forces. Figure 7 represents total energy versus lattice constant of 8 atoms surface, at equilibrium lattice constant the total energy is too small compare with 8 atoms core nanocrystal.
Figures 8 and 9 show the variation of the energy gap, valance and conduction bands of GaP nanocrystals with
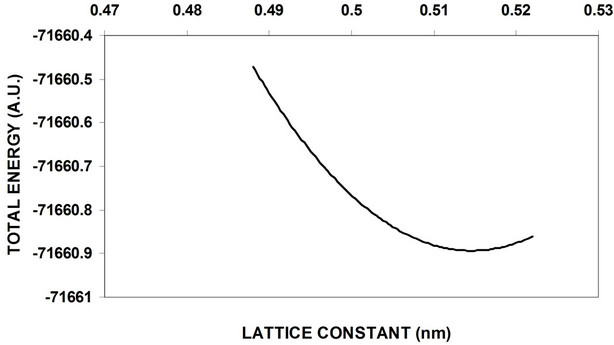
Figure 5. Optimization of 64-atom core lattice constant of GaP nanocrystals.
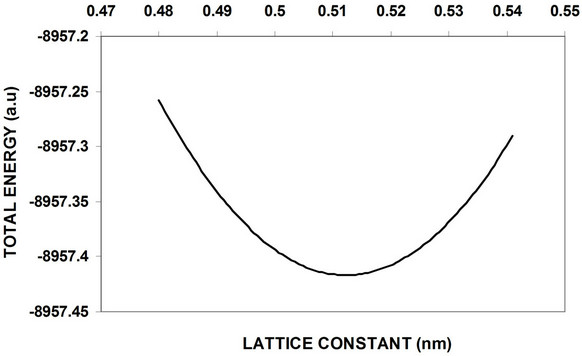
Figure 6. Total energy versus lattice constant of 8-atom core (LUC) of GaP nanocrystalls.
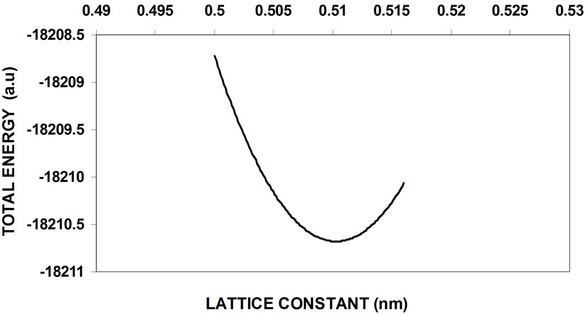
Figure 7. Total energy versus lattice constant of 8-atom oxygenated (001)-(1 × 1) surface of GaP.

Figure 8. Energy gap variation with the number of core atoms of GaP nanocrystals.

Figure 9. Valence and conduction bands variation with the number of core atoms of GaP nanocrystals.
the number of core atoms. Cubic cells (8, 64 atoms) have wider bands than parallelepiped cells (16, 54 atoms). This effect was in agreement with previous studies [8,9, 12,14]. From Figure 10, we can notice that the value of cohesive energy decreases with increasing of the number of atoms per LUC reflecting the strong contribution of atoms. The cohesive energy increment is not linear and the rate of change of larger crystals sizes decreases and tends to be a constant value. This behavior shows the shape effect which appears because of shape conversion from cubic cell (8, 64) to the parallelepiped cell (16, 54) [10,25,26].
The results of density of states of core 8 atoms LUC and surface 8 atom as a function of energy levels are

Figure 10. Cohesive energy variation with the number of core atoms of GaP nanocrystals.

Figure 11. Density of states of 8 core atoms of GaP. Valence bands are shown with bold lines while conduction bands are shown with ordinary lines. The energy gap is shown between the two bands, where Eg = 1.6 eV.
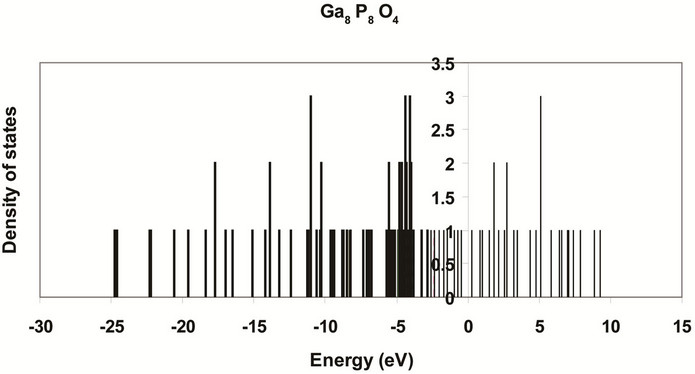
Figure 12. Surface density of states of 8-atom oxygenated (001)-(1 × 1) for a2. Valence bands are shown with bold lines while conduction bands are shown with ordinary lines. The energy gap is shown between the two bands, where Eg = 0.22 eV.
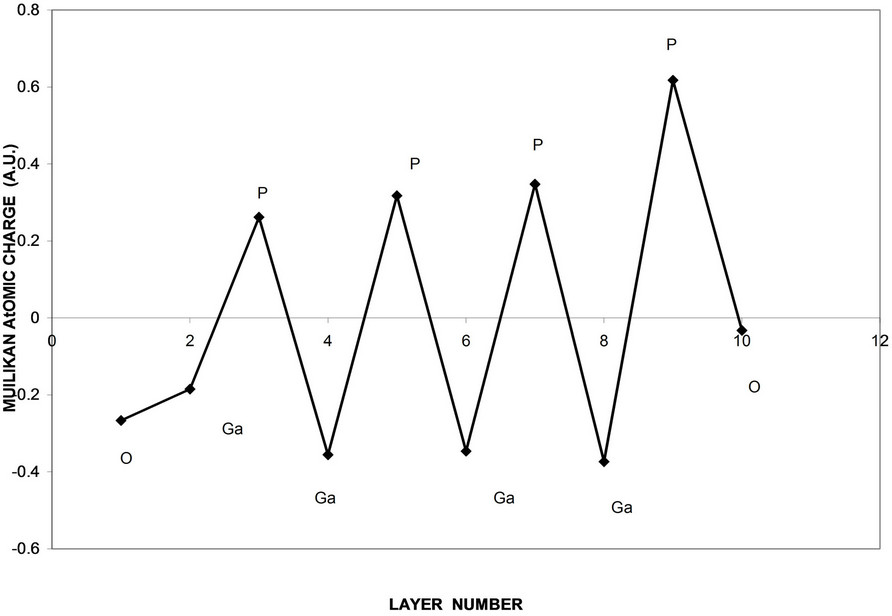
Figure 13. Atomic charges as a function of layers depth of oxidized GaP nanocrystal surface using slap geometry.
shown in Figures 11 and 12. The results that the core states show larger energy gap and smaller valence and conduction bands. Owing to perfect symmetry of the core, the core states are more degenerate. As we move to the surface we see low degenerate and small energy gap and wider valance and conduction bands. This reflects the broken symmetry and discontinuity at the surface and existence of new kind of atoms (oxygen atoms), and the variation of bond lengths and angles [27,28]. Figure 13 shows the atomic charges of oxidized Ga8P8O4 surface as a function of layer depth using the slab geometry method. The first and the last negative charged atoms in the figure are oxygen atoms. These atoms are neighboring the outermost surface P atoms that have positive charges. The Ga atoms have negative charges. This trend of charges is consistent with our previous assumptions of thickness of surface reconstruction effects. These charges are triggered by the high electron affinity of oxygen surface atoms [9,10,29].
5. Conclusion
The obtained results show the shape and bounding surface of nanocrystal are important factors for energy gap, as well as the valence and conduction bands. Surface and core parts have approximately the same lattice constant and this fact reflects the good adherent of oxide layer at the surface. Moreover the cohesive energy decreases with number of core atoms in LUC. The value of the energy gap is extremely lower for the surface than the core this reflecting the fact that core part is more degenerate and smaller valence and conduction bands are encountered than the surface part. This may be attributed to the shape and kind of surfaces which have a pronounced effect on the electronic structure of the core of nanocrystals. The atomic charges are triggered by the higher electron affinity of oxygen surface. The surface has damping oscillatory successive negative and positive layer charges.
REFERENCES
- D. W. Plamer, “Semiconductors Information,” 2006. http://www.semiconductors.co.uk
- L. T. Fu, H.-T. Cong, et al., “Fabrication and Visible Emission of Single-Crystal Diameter-Modulated Gallium Phosphide Nanochains,” Journal of Applied Physics, Vol. 107, No. 12, 2010, Article ID: 124321.
- R. Kirshcman, “High Temerature Electronics,” Wiley, Hoboken, 1999.
- L. E. Brus, “Electron-Electron and Electron-Hole Interactions in Small Semiconductor Crystallites: The Size Dependence of the Lowest Excited Electronic State,” Journal of Chemical Physics, Vol. 80, No. 9, 1984, pp. 4403- 4409. doi:10.1063/1.447218
- M. G. Bawendi, M. L. Steigherwald and L. E. Brus, “The Quantum Mechanics of Larger Semiconductor Clusters,” Annual Review of Physical Chemistry, Vol. 41, 1990, pp. 477-496.
- A. P. Alivisatos, “Perspectives on the Physical Chemistry of Semiconductor Nanocrystals,” Journal of Physical Chemistry B, Vol. 100, No. 31, 1996, pp. 13226-13239. doi:10.1021/jp9535506
- R. Evarestov, M. Petrashen and E. Lodovskaya, “The Translational Symmetry in the Molecular Models of Solids,” Physica Status Solidi B, Vol. 68, No. 1, 1975, pp. 453-461.
- A. Harker and F. Larkins, “A Large Unit Cell Semiempirical Molecular Orbital Approach to the Properties of Solids. I. General Theory,” Journal of Physics C: Solid State Physics, Vol. 12, No. 13, 1979, pp. 2487-2495.
- I. O. Radi, M. A. Abdulsattar and A. M. Abdul-Lettif, “Semiempirical LUC-INDO Calculations on the Effect of Pressure on the Electronic Structure of Diamond,” Physica Status Solidi (b), Vol. 244, 2007, pp. 1304-1317.
- N. H. Aysa, M. A. Abdulsattar and A. M. Abdul-Lettif, “Electronic Structure of Germanium Nanocrystals Core and (001)-(1 × 1) Oxidised Surface,” Micro & Nano Letters, Vol. 6, No. 3, 2011, pp. 137-140. doi:10.1049/mnl.2010.0154
- M. A. Abdulsattar, “Mesoscopic Fluctuations of Electronic Structure Properties of Boron Phosphide Nanocrystals,” Electronic Materials Letters, Vol. 6, No. 3, 2010, pp. 97-101. doi:10.3365/eml.2010.09.097
- M. H. Sanni, et al., Physical Review B, Vol. 76, 2007, Article ID: 035417.
- H. M. Abduljalil, M. A. Abdulsattar and S. R. Al-Mansoury,” SiGe Nanocrystals Core and Surface Electronic Structure from ab Initio Large Unit Cell Calculations,” Micro & Nano Letters, Vol. 6, No. 6, 2011, p. 386. doi:10.1049/mnl.2011.0115
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, et al., “Gaussian 03,” Revision B. 01, Gaussian, Inc., Pittsburgh, 2003.
- M. A. Abdulsattar, “Ab Initio Large Unit Cell Calculations of the Electronic Structure of Diamond Nanocrystals,” Solid State Sciences, Vol. 13, No. 5, 2011, pp. 843- 849. doi:10.1016/j.solidstatesciences.2011.03.009
- J. P. Perdew, K. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996, pp. 3865-3868.
- W. Kohn and I. J. Sham, “Self-Consistent Equations Including Exchange and Correlation Effects,” Physical Review, Vol. 140, No. 4A, 1965, pp. 1133-1138.
- R. M. Dreizler and E. K. U. Gross, “Density Functional Theory,” Springer-Verlag, Berlin, 1990.
- R. G. Parr and W. Yang, “Density Functional Theory of Atoms and Molecules,” Oxford, New York, 1989.
- D. C. Langreth and M. J. Mehl, “Beyond the Local-Density Approximation in Calculations of Ground-State Electronic Properties,” Physical Review B, Vol. 28, No. 4, 1983, pp. 1809-1834. doi:10.1103/PhysRevB.28.1809
- A. D. Becke, “Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior,” Physical Review A, Vol. 38, No. 6, 1988, pp. 3098-3100. doi:10.1103/PhysRevA.38.3098
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, “Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation,” Physical Review B, Vol. 46, 1992, p. 6671.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Physical Review B, Vol. 48, 1993, p. 4978.
- J. P. Perdew and Y. Wang, Physical Review B, Vol. 45, No. 13, 1992, p. 244.
- N. A. Nama, M. Abdulsattar and A. Abdul-Lettif, “Surface and Core Electronic Structure of Oxidized Silicon Nanocrystals,” Journal of Nanomaterials, Vol. 2010, 2010, Article ID: 952172.
- S. Razaq, MSc. Thesis, University of Babylon, Babylon, 2010.
- H. Sigg, U. Denker, M. Stoffel and O. Schmidt, PSI Scientific Report, Vol. VII, 2002.
- W. C. Butterman and J. D. Jorgenson, “Mineral Commodity Profiles: Germanium,” Open-File Report 2004- 1218, US Geological Survey.
- G. C. McIntosh, M. Yoon, S. Berber and D. Tohmanek, “Diamond Fragments as Building Blocks of Functional Nanostructures,” Physical Review B, Vol. 70, No. 4, 2004, Article ID: 045401. doi:10.1103/PhysRevB.70.045401

