Received 10 May 2016; accepted 3 June 2016; published 6 June 2016

ABSTRACT

In this study, we reconsider the effect of variable transformations on income inequality. Under the assumption that the theorems should hold for all income distributions, earlier given sufficient conditions are also necessary. Different versions of the conditions are compared. Furthermore, one can prove that the assumption of continuity of the transformations can be implicitly included in the necessary and sufficient conditions, and hence, it can be dropped from the assumptions. The effects of two transformations on income inequality are compared.

Keywords:

Discontinuity, Income Distribution, Income Inequality, Lorenz Dominance, Tax Policy, Transfer Policy

1. Introduction

It is a well-known fact that variable transformations are valuable in considering the effect of tax and transfer policies on income inequality. The transformation is usually assumed to be positive, monotone increasing and continuous. Under the assumption that the theorems should hold for all income distributions, conditions given earlier are both necessary and sufficient [1] [2] . Hemming and Keen [3] have given an alternative version of the conditions. Recently, Fellman [2] [4] also discussed discontinuous transformations. One general result is that continuity is a necessary condition if the transformation should preserve or reduce income inequality. If the transformation is considered as a tax or a transfer policy, the transformed variable is either the post-tax or the post- transfer income. In this study, we reconsider the effect of variable transformations on the redistribution of income. Two transformations are studied and their effects on income inequality are compared.

2. Properties of a Transformed Variable

Consider the income X with the cumulative distribution function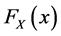, the frequency distribution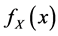, the mean, and the Lorenz curve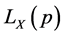. We assume that X is defined for 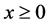and that is continuous. Furthermore, we consider the transformation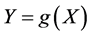, where 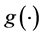is non-negative and monotone increasing. A fundamental theorem concerning the effect of income transformations on Lorenz curves was first given by Fellman [5] , Jakobsson [1] , and Kakwani [6] and later by Fellman [7] [8] . Hemming and Keen [3] gave a new condition for the Lorenz dominance. We have

Theorem 1. Let 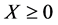be a random variable with an arbitrary continuous frequency distribution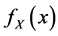, mean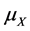, and the Lorenz curve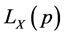. Let 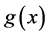be positive, continuous, and monotone increasing, let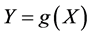, and let 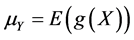exist. Then, the Lorenz curve of Y exists and the following results hold:

1) if is monotone decreasing

2) if is constant

3) if is monotone increasing.

Proof: From the fact that

,

it follows that exists.

The case 2) follows immediately from the fact that the Lorenz curve remains when linear transformation is performed. Consider the difference

(1)

By definition,. First, we assume that is continuous and monotone decreasing for. Then attains zero only once, being first positive and then negative. Hence, the difference and the case 1) is proved.

For the case 3), is monotone increasing for. Also in this case. The difference attains zero only once, being first negative and then positive. Hence, and the case 3) is proved.

If we consider tax policies, x is the pre-tax income and the function is the after-tax income and the ratio is the relative tax. If the ratio is monotonically decreasing, is monotone increasing and the tax policy is progressive. Hence, Theorem 1 1) states the well-known result that progressive taxes reduce income inequality.

In addition, if we consider income increases and that is the increased income and that 1) holds then the income increase reduces the income inequality.

According to Theorem 1, we obtain in 1) a sufficient condition that the transformation g(x) results in a new income distribution, which Lorenz dominates the initial one. What can be said about necessary conditions? If we analyze the proof of Theorem 1, we observe that the difference

(2)

plays a central role. For a transformation for which the quotient is not monotone decreasing for all, an income distribution can be chosen so that the result in the proof holds, i.e. dominance is obtained. We have only to choose and so that is non-negative for all p. For example if the quotient is both increasing and decreasing we choose the distribution so that is positive only in an interval where is monotone decreasing.

The sufficient condition of Hemming and Keen [3] is (with our notations) that for a given distribution the function crosses the line once from above. The Hemming-Keen condition is equivalent with the condition that crosses the level from above, which is easier to compare with ours. We ob-

serve that if their condition holds then the integrand in (2) starts from positive values, changes its sign once, and ends up with negative values.

If we demand necessary conditions, they must be formulated as a condition that holds for all income distributions. The condition of Hemming and Keen must be that must satisfy the condition “crossing once from above for all distributions” [3] . We start with the condition in Theorem 1 1) and prove that it is also necessary. This can be proved in the following way ( [1] [9] , p. 189). Let a transformation satisfy the initial conditions (positive, continuous, and monotone increasing) and let be increasing within some interval (). Now, we prove that there exists an income distribution such that the transformed variable does not Lorenz dominate the initial variable X.

Consider an income distribution

(3)

For the pair, Theorem 1 3) holds and the transformation results in a new variable Y, which is Lorenz dominated by the initial variable X. This result indicates that if is monotone increasing even in a short interval, then there are income distributions such that the transformation cannot result in Lorenz dominance. Hence, if we demand that, for all distributions, the transformed variable shall Lorenz dominate X then the condition in Theorem 1 1) is necessary. In the example considered above, the Hemming-Keen condition is not satisfied. Consequently, if is not monotone decreasing then there are distributions for which the Hemming-Keen condition does not hold. On the other hand, if we assume that is monotone decreasing then satisfies the condition “crossing once from above for every distribution”. Hence, our condition and the Hemming-Keen condition are equivalent as necessary conditions. In a similar way, we can prove that if the other results in Theorem 1 should hold for every income distribution the conditions in 2) and in 3) are also necessary.

Now, we follow [8] and drop the assumption that is continuous and consider discontinuous functions. What can be said about the case that is discontinuous? Assume that is still positive and monotone increasing and satisfies the condition that exists for every stochastic variable X, whose distribution satisfies the general conditions given above, then the discontinuities can only consist of denumerable finite positive jumps. Now we will prove that if there exists one such jump there exists at least one distribution such that the transformation does not Lorenz dominate the initial variable X.

Let a be a discontinuity point such that and where. If should be monotone increasing, we have to assume that. Let and, then

(4)

Hence, we note that the quotient cannot be monotone decreasing within a short interval. Choose so small that the point a is the only discontinuity point within the interval (later we may reduce h even more).

Consider the uniform distribution

(5)

For this variable X, the mean is. For the transformed variable Y = g(X), the mean is

(6)

where and.

If then, , , , and consequently,.

Assume that we choose h so small that. Consider now

(7)

To obtain Lorenz dominance, the integrand must start from positive (non-negative) values and then change its sign once and become negative in such a manner that the difference D (p) starts from zero and then attains positive values, whereupon it decreases back to zero.

The sign of the integrand depends on the factor, which starts from the value

(8)

If we assume that h satisfies the earlier conditions and furthermore, the integrand in (7) starts

from negative values, and consequently, the whole integrand is negative and the difference starts from negative values. For the corresponding income distribution, the transformed variable Y does not Lorenz dominate the initial variable X. Hence, the continuity of is also a necessary condition if we demand that the transformed variable should Lorenz dominate the initial variable irrespectively of the distribution f_x(x). However, we noted already that the continuity is a necessary condition for the monotone decreasing assumption in 1). From this, it follows that the condition in Theorem 1 1) implies continuity, and hence, the explicit assumption of continuity can be dropped. In a similar way, we can obtain the same result if we study the condition in 2). However, in the case 3) the discontinuity does not jeopardize the monotone increasing property of the quotient, and the result in Theorem 1 3) holds even if the function is discontinuous. Therefore, also in this case we can drop the explicit continuity assumption.

Summing up, for arbitrary distributions, , the conditions in Theorem 1 1), 2), and 3) are both necessary and sufficient for the dominance relations and the additional assumption about the continuity of the transformation can be dropped. We obtain a generalized theorem ( [1] [2] [6] - [8] ).

Theorem 2. Let be a random variable with an arbitrary continuous distribution, mean, and the Lorenz curve. Let be a positive, monotone increasing function, let, and let exist. Then the Lorenz curve of Y exists and the following results hold:

1) if and only if is monotone decreasing

2) if and only if is constant

3) if and only if is monotone increasing.

Remark. From the discussion above, it follows that only in the case 3) can the transformation be discontinuous.

If we apply these results on income raise policies and on tax policies the transformed variable is the income after the income raise or after the taxation (cf. e.g. [5] [10] - [12] ). We obtain that only income raise policies that (with respect to the initial income) give decreasing relative salary increments result in a decreased income inequality for all initial income distributions. An analogous result holds for progressive tax policies.

3. Comparison of Two Transformed Variables

Theorem 1 can be used when the effect of a given tax or salary policy is studied. If several policies are to be compared, the following theorems, which are generalizations of Theorem 1 and Theorem 2, will prove valuable. The generalization of Theorem 1 was first presented by Fellman [10] and proved in [13] . Wilfling [14] later regenerated this theorem. The Hemming-Keen theorem was primarily given in this context. Consider two policies (transformations) and. Following Fellman ( [10] [13] ), we have

Theorem 3. Let X be a continuous and non-negative random variable with an arbitrary distribution, mean, and the Lorenz curve. Let and be continuous, non-negative and monotone increasing, let and, and let and exist. If the Lorenz curves of Y and Z are and, respectively, then the following results hold:

1) if is monotone decreasing

2) if is constant

3) if is monotone increasing.

Proof: If (constant), then and the case 2) follows immediately from Theorem 1. If we assume that is monotone decreasing for x > 0, then attains the value zero only once, be-

ing first positive and then negative. Hence, and the case 1) is proved. The case 3) can be proved if we let and exchange their roles and the proof of the case 1) is performed.

Now we study two different salary increase policies.

Example ( [13] )

1. The salary increases are of the same size regardless of the previous salary

In this case, and the ratio is strictly decreasing.

2. The salary increases are of the same size up to a certain salary level, thereafter they are strictly proportional. Now the transformation function is

(9)

The continuity of for demands that and. The ratio is

(10)

and is monotone decreasing.

In both cases, the ratio is monotone decreasing and the policies reduce the income inequality. Now we compare the two policies under the assumption that both give the same increase of the initial mean from to. For the increased means, we obtain

and

(11)

If the two increase means should be identical, we obtain the relation

and.

If we apply Theorem 3 on our two policies, we obtain

(12)

Hence, the ratio is monotone decreasing for all x and the transformation reduces the inequality more than the transformation.

If we assume that the conditions in Theorem 3 should hold for every income distribution, we can drop the condition that and are continuous and we can prove in a similar way as above that the conditions are also necessary. We obtain

Theorem 4. Let X be a continuous and non-negative random variable with an arbitrary distribution, mean, and the Lorenz curve. Let and be non-negative and monotone increasing, let and, and let and exist. If the Lorenz curves of Y and Z are and, respectively, then the following results hold:

1) if and only if is monotone decreasing

2) if and only if is constant

3) if and only if is monotone increasing.

In a similar way as above, we obtain that the discontinuities in and can only be finite positive jumps. If the condition in Theorem 4 1) holds, then can be discontinuous, but can be discontinuous only at such points where is discontinuous, and additionally, the corresponding jumps must

be such that is monotone decreasing. In 2) and can be discontinuous only at the same points, and additionally, the corresponding jumps must be such that remains constant. In 3) can be discontinuous, but can be discontinuous only at such points where is discontinuous, and additionally, the corresponding jumps must be such that is monotone increasing.

Remark. Theorems 3 and 4 are generalized versions of Theorems 1 and 2, respectively. This is clear if we introduce the simplified condition.

4. Conclusions

Redistributions of income have commonly been defined as transformations of the initial income variable. The transformations are mainly considered as tax or transfer policies yielding post-tax or post-transfer incomes, and therefore, the transformations are usually assumed to be positive, monotone increasing, and continuous. Recently, discontinuous transformations have been discussed. Particularly, we were interested in determining if one can drop the assumptions of continuity of the transformations.

In this study, we considered the effect of variable transformations on the redistribution of income. The aim was to compare and generalize the conditions considered in earlier papers. The fundamental concern has been the Lorenz ordering between the initial and transformed income. We have obtained that, if we demand sufficient and necessary conditions, theorems earlier obtained still hold and the continuity assumption can be implicitly included in the general conditions. Especially, we have considered the optimal cases that the transformed variable Lorenz dominates the initial one. In applications, this case is important because it yields policies which reduce income inequality. The main result is that continuity is a necessary condition if income inequality should remain or be reduced.

Empirical applications of the optimal policies of classes of transfer policies and of tax policies considered here have been discussed in Fellman et al. [12] [15] . There we developed “optimal yardsticks” to gauge the effectiveness of given real tax and transfer policies in reducing inequality.

Acknowledgements

This study was supported by grants from the Finnish Society of Sciences and Letters and Magnus Ehrnrooth Foundation.

Cite this paper

Johan Fellman, (2016) Transformations and Lorenz Curves: Sufficient and Necessary Conditions. Theoretical Economics Letters,06,442-449. doi: 10.4236/tel.2016.63050

References