Theoretical Economics Letters
Vol.05 No.02(2015), Article ID:55387,7 pages
10.4236/tel.2015.52028
Directionally Bounded Utility and the Executive Pay Puzzle
Edoh Y. Amiran1, Daniel A. Hagen2
1Department of Mathematics, Western Washington University, Bellingham, USA
2Department of Economics, Western Washington University, Bellingham, USA
Email: edoh.amiran@wwu.edu, dan@hagen.net
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 February 2015; accepted 31 March 2015; published 7 April 2015
ABSTRACT
The pay of CEOs and other top executives has risen disproportionately relative to other earnings. We provide a supply-side explanation based on utility theory using directionally bounded utility functions. As overall income levels have grown, the amount of compensation required to induce top executives to sacrifice a quiet life has risen. We show that directionally bounded utility functions predict a general rise in compensation for stress. More importantly, such utility functions can be used to explain why the CEO pay ratio has risen at an increasing rate, something which other approaches have difficulty explaining.
Keywords:
Executive Pay, Utility Theory, Substitution Effects

1. Introduction
Pay of top executives in the United States has risen relative to average earnings. This rise began during the early 1970s, and accelerated in subsequent years. The general trend has continued, after an adjustment, even following the burst of two prominent asset bubbles. A number of economic models and mechanisms have been proposed as explanations for the drastic rise. The puzzle is that no theoretical model of the market for executives has fully accounted for the nature of the rise. Particularly puzzling is the observed acceleration in the rise. The long-term trend shows the CEO pay ratio rising at a rapidly increasing rate.
Explanations for the rapid rise in executive pay fall into three broad categories. Some explanations focus on the demand for talent. These demand-driven explanations focus on skill-biased technological change and other factors that increase the value of executives to the firm. For example, see Kaplan and Rauh [1] which looked at the compensation of the top 1 percent of US earners.
A second category of explanations considers changes in social customs and in corporate culture and the re- sulting ability of managers to bargain for higher levels of compensation. These managerial power explanations include various mechanisms. Examples include the increasing acceptability of higher rewards in periods with large returns to shareholders and the rigidity of the number of shares included in stock options. See Shue and Townsend [2] and Bebchuk and Grinstein [3] for discussions of this approach, and Snyder [4] for a critique of this view of bargaining. Frydman and Jenter [5] reviews the relationship between pay and firm performance, considering both demand-side explanations and managerial-power explanations, and finds that neither approach is fully consistent with the available evidence.
A final category of explanations focuses on the incentives required to attract executives. These supply-driven explanations include incentives for assuming risks, especially since executives might be averse to risk by com- parison to the firms which might seek the greater rewards associated with greater risks; tournament type in- centives, which may change with the broadening of the international market; and the use of compensation as a signal of confidence in the executives. For examples and discussions of supply-driven arguments see Aggarwal and Samwick [6] and Spatt [7] .
The principal problem with the standard supply-driven arguments and also with managerial-power arguments is that in these theories the executive pay ratio should not rise at a rapidly increasing rate given the steady rise in the underlying economic factors. The principal problem with demand-driven arguments is that they too would predict a rise in executive pay that is proportional to the value generated for the firm.
The explanation we propose falls into the supply-side category. It is different in that we consider the role of directionally bounded utility, and its unique implications for substitution between material consumption and a quiet life. We show how plausible utility functions can explain an increase in the amount of compensation re- quired to maintain interest in stressful jobs as the general level of pay in the economy increases. We also show that this can cause the ratio of CEO pay to rise at an increasing rate.
2. Directionally Bounded Utility
Many commonly used neoclassical utility functions are not directionally bounded. Functions that are not direc- tionally bounded have the property that any level of utility within the range of the function can be obtained by increasing the consumption of any one good (assuming the consumption quantities of the other goods are non- zero). This implies rather extreme behavior regarding substitution. Consider, for example, the familiar Cobb- Douglas utility function, and assume that one of the goods is raisins. Given the functional form, any level of utility can be achieved by increasing the consumption of raisins, regardless of the consumption quantities of the other goods. This implies that there is some additional quantity of raisins that would compensate the consumer for the loss of nearly all other goods, so long as the quantities of those goods remain positive. The consumer would be willing to give up nearly all of her housing, entertainment, and other types of food in exchange for additional raisins. She would also be willing to give up nearly all non-market goods, including air quality and national defense, in exchange for a finite incremental increase in her consumption of raisins. This is referred to as “hypersubstitutability” [8] . The existence of universal hypersubstitutability, implicit in functions such as the Cobb-Douglas, seems highly implausible. While it may appear that this property only has implications at ex- treme levels of consumption, it has been shown to have important implications in contexts where the changes in consumption quantities are not large [8] [9] .
Formalizing this concept for the case of a non-market good, consider a Cobb-Douglas utility function of the form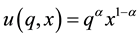 , where
, where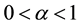 . Assume that x is a composite bundle of market goods and q is a non- market good. Real willingness to accept compensation (WTA) for a decrease in q can be defined as the mi- nimum amount of x that a consumer is willing to receive in exchange for that decrement of q. For any positive initial amount of the goods
. Assume that x is a composite bundle of market goods and q is a non- market good. Real willingness to accept compensation (WTA) for a decrease in q can be defined as the mi- nimum amount of x that a consumer is willing to receive in exchange for that decrement of q. For any positive initial amount of the goods 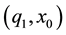 corresponding to the initial level of utility
corresponding to the initial level of utility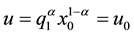 , WTA remains finite for the Cobb-Douglas utility function, even when the amount of the non-market good is decreased to near zero. Moreover, the amount of compensation as a proportion of the initial income depends only on the initial and final amounts of the non-market good. Computationally, for any
, WTA remains finite for the Cobb-Douglas utility function, even when the amount of the non-market good is decreased to near zero. Moreover, the amount of compensation as a proportion of the initial income depends only on the initial and final amounts of the non-market good. Computationally, for any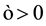 , if q is reduced to
, if q is reduced to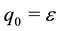 , then
, then 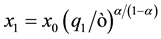 compensates for that reduction, that is
compensates for that reduction, that is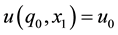 , and
, and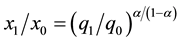 . In com- modity space, all indifference curves for the utility function are asymptotic to the goods’ axes, and hence intersect
. In com- modity space, all indifference curves for the utility function are asymptotic to the goods’ axes, and hence intersect 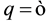 at a finite value of x. In other words, the consumer would be willing to accept the loss of nearly all of the non-market good (leaving only
at a finite value of x. In other words, the consumer would be willing to accept the loss of nearly all of the non-market good (leaving only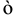 ) in exchange for a sufficiently large increment in market goods. Similarly, for this utility function, the consumer would be willing to forgo nearly all consumption of market goods in exchange for a sufficiently large increment of the non-market good.
) in exchange for a sufficiently large increment in market goods. Similarly, for this utility function, the consumer would be willing to forgo nearly all consumption of market goods in exchange for a sufficiently large increment of the non-market good.
Hypersubstitutability in this case results from the property that there is no bound on the contribution to utility from increasing the consumption of any one good. In contrast, directionally bounded utility functions contain limits on the contributions that individual goods can provide. With directionally bounded functions there are limits on the level of utility that can be obtained by increasing the consumption of any one good. While such functions may be monotonically increasing in every direction, as utility rises due to an increase in a single good the level of utility approaches some asymptotic value rather than increasing without bound. The function is bounded in the direction of each good. Directionally bounded utility functions impose non-local restrictions on substitution, while allowing for continuous substitutability at the margin. It is possible to specify functions of this type that conform to all of the axioms of neoclassical consumer theory.
In what follows we make use of the formal definition of directionally bounded utility first proposed by Amiran and Hagen [9] . Consider a utility function 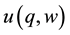 that depends continuously on non-market and market goods whose consumption levels are
that depends continuously on non-market and market goods whose consumption levels are 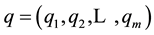 and
and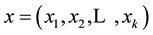 . For what follows we require that the utility function be directionally bounded in the directions of x, although it is also possible (and likely) that the function is directionally bounded in the directions of q.
. For what follows we require that the utility function be directionally bounded in the directions of x, although it is also possible (and likely) that the function is directionally bounded in the directions of q.
Definition 1: Directionally Bounded Utility. The utility function 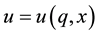 is directionally bounded in the directions of x if the maximum level of utility that can be achieved as the subset of goods x increases is less than the maximum level of utility that can be achieved as all goods increase. In other words, writing
is directionally bounded in the directions of x if the maximum level of utility that can be achieved as the subset of goods x increases is less than the maximum level of utility that can be achieved as all goods increase. In other words, writing 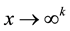 for
for 

In the above definition, we assume that the limits exist but include the possibility that utility approaches in- finity (that is, increases without bound). However, the left hand side in the inequality must be finite.
3. Directionally Bounded Utility and Executive Pay
Modeling the behavior of executives through their utility we derive equilibrium levels of relative compensation. We assume that higher level positions impose additional stress on the executives holding those positions, and that adequate compensation for this added stress is provided in equilibrium. WTA in this context is the mini- mum payment necessary to compensate executives at a particular level for the added stress (loss of a “quiet life”) associated with the position. We assume that there is some base level of stress associated with a low-level job, and that the compensating pay differential is a function of the difference in stress relative to the base level. Executives might be able to bargain for a level of compensation in excess of WTA, the resulting surplus being a function of their bargaining power. In what follows we assume that the bargaining power of executives remains constant over time. This allows us to isolate supply-side effects, however the model can be easily modified to include bargaining effects. In this context, where bargaining power is held constant, changes in executive com- pensation will be directly proportional to changes in WTA.
Our focus is on explaining the sudden and rapid acceleration in the pay of CEOs (and other high-level ex- ecutives) relative to workers as a whole. We claim that this pattern can be explained using utility theory through the dependence of WTA on base income and the variance in stress across positions. It is assumed, in the model, that base income changes over time. We also consider what happens if the differential in stress increases over time.
We describe the executive’s utility in terms of the consumption of two goods, a composite good which measures the executive’s level of material consumption and the “quietness” of the executive’s life, which is inversely related to the level of stress associated with the job. Denote the variable measuring the “quietness” of life by q. Total real compensation is given by x. Suppose that there is a base level


Suppose that the compensation for the job with the base-level of stress is 







In the presence of some bargaining power, the employee would be able to receive greater compensation, and we assume that the increased compensation becomes

We show that with directionally bounded utility, two phenomena may occur. First, as the base level of income 
While similar features appear with any directionally bounded utility function, we illustrate the occurrence of the two phenomena with a specific form of utility. Suppose that the employee’s utility, 





From 

Notice that since




In what follows we consider two employees, an executive with a high level of stress (and a lower level of quietness) and a base-level employee with a lower loss of quietness. Let 








The change in executive pay is captured by the change in the pay ratio


Theorem 1 Suppose that employees have a directionally bounded utility function as specified in Equation (1). Let 

Proof. Since these combinations occur frequently in calculations, define

Direct calculations yield

Now 





Calculating the terms in Equation (5),



Since



Now 









This last expression is independent of 
Theorem 1 examines the ratio of compensations required by two individuals, one with a higher level of stress than the other. Since employees become more reluctant to give up a quiet life as their compensation rises, it follows that the ratio of compensations will rise even as the level of compensation of both workers rises. Or said another way, the compensation required to keep the more stressed worker would grow at a greater proportional rate as a result of general wage increases.
Note that the specific functional form in Equation (1) was used to illustrate the type of utility that leads to the conclusion in the theorem. In fact, any directionally bounded utility function with increasing convexity at higher levels of initial income (keeping the quality variable fixed) would yield similar results. Amiran and Hagen [8] show that for directionally bounded utility functions there is a critical value 



Theorem 2 Suppose that employees have a directionally bounded utility function so that willingness to accept compensation for any predetermined loss of a quiet life, relative to a fixed starting amount of quietness, increases without bound as income reaches a critical value


Proof. It follows from the assumptions that even for the base-level worker, with this worker’s lower value of stress, there is a critical value 








Corollary 1 In the setting of Theorem 2, suppose that the loss of quietness associated with the work of an executive increases over time. Then 
Proof. Denote the values of WTA at the initial time by 






Theorem 2 demonstrates that the executive pay ratio 
4. Casual Empiricism
Many factors affect the relative level of executive pay. A full explanation of the data on executive pay would require separating the different influences on pay and components of compensation, and is beyond the scope of this paper. However, we examine whether the directionally bounded utility model suggested here fits the general shape of the data. In particular, we are interested in discovering whether the underlying trend in the executive pay ratio is consistent with the predictions of our utility model. This imprecise empirical test is based on readily available data and is conducted graphically. The resulting “visual fit” of the model to the data is intended to provide a crude test of the plausibility of our model, rather than a formal statistical test of its sufficiency or accuracy.
The data we use gives the ratio of CEO compensation to average compensation in the corresponding sector as calculated by Mishel and Davis [10] for certain years between 1965 and 2013. (The authors do not calculate the ratio for every year.) This ratio is the observed value of







Figure 1 shows the observed ratio of CEO pay to average pay in the corresponding sector (from [10] ), our base income index (rescaled to match the starting point for the CEO pay ratio), and the “fitted” trend value for 
Our utility model is capable of generating a trend that matches the underlying trend in the observed series, but of course the model cannot explain the temporary deviations from the trend associated with asset market bubbles or other temporary deviations from the trend. Changes in the rate of substitution between executive pay and stress provide a possible explanation for the trend in the executive pay ratio during the period examined. Direc- tionally bounded utility functions can be used to model the changing rate of substitution in a way that represents this behavior.
5. Summary and Conclusions
The above analysis shows that utility theory can provide a missing piece of the executive pay puzzle. Spe- cifically, it helps to explain why the executive pay ratio has been increasing at an increasing rate. Our utility model explains an underlying trend in relative compensation when higher level positions involve a tradeoff between pay and stress. The rate of substitution between material consumption and a quiet life reflects the will- ingness of an employee to accept compensation for an increase in stress. Restrictions on this rate of substitution can be captured by directionally bounded utility functions, providing an explanation for the underlying trend in the pay ratio.
Figure 1. Ratio of CEO pay to average sector pay.
On the other hand, there are important deviations from the trend that cannot be explained by our utility model. A complete explanation for the behavior of the executive pay ratio requires the incorporation of other factors. For example, the mechanism of paying top executives with stock options may help explain the spike in exe- cutive pay during the dot-com boom. Similarly, changes in the behavior of owners and regulators may have also contributed to changes in the pay ratio, whether temporary or more persistent.
In the context of utility theory our findings lead in two directions. First, in choosing a utility model, it is use- ful to consider whether significant restrictions on substitution arise. If significant restrictions on substitution are suspected, then a directionally bounded utility function may explain phenomena that are otherwise difficult to analyze. Directionally bounded utility has the advantage that it does not impose hypersubstitutability. Second, an appropriate utility model may help to explain an underlying trend but leaves room for other explanations of be- havior. As in our example of executive pay, utility theoretic explanations can be viewed as complementary to other explanations, including explanations based on institutional change.
References
- Kaplan, S.N. and Rauh, J. (2013) It’s the Market: The Broad-Based Rise in the Return to Top Talent. Journal of Economic Perspectives, 27, 35-56. http://dx.doi.org/10.1257/jep.27.3.35
- Shue, K. and Townsend, R. (2014) Growth through Rigidity: An Explanation for the Rise in CEO Pay. Tuck School of Business Working Paper No. 2424860, Chicago Booth Research Paper No. 14-22. http://ssrn.com/abstract=2424860 http://dx.doi.org/10.2139/ssrn.2424860 >http://dx.doi.org/10.2139/ssrn.2424860 http://dx.doi.org/10.2139/ssrn.2424860
- Bebchuk, L. and Grinstein, Y. (2005) The Growth of Executive Pay. Oxford Review of Economic Policy, 21, 283-303. http://dx.doi.org/10.1093/oxrep/gri017
- Snyder, F.G. (2003) More Pieces of the CEO Compensation Puzzle. Delaware Journal of Corporate Law, 28, 129- 183.
- Frydman, C. and Jenter, D. (2010) CEO Compensation. Rock Center for Corporate Governance at Stanford University Working Paper No. 77. http://ssrn.com
- Aggarwal, R. and Samwick, A. (1999) The Other Side of the Trade-Off: The Impact of Risk on Executive Compensation. Journal of Political Economy, 107, 65-105. http://dx.doi.org/10.1086/250051
- Spatt, C. (2006) Executive Compensation and Contracting. Working Paper, Tepper School of Business, Carnegie Mellon University, Pittsburgh.
- Amiran, E.Y. and Hagen, D.A. (2003) Willingness to Pay and Willingness to Accept: How Much Can They Differ? Comment. American Economic Review, 93, 458-463. http://dx.doi.org/10.1257/000282803321455430
- Amiran, E.Y. and Hagen, D.A. (2010) The Scope Trials: Variation in Sensitivity to Scope and WTP with Directionally Bounded Utility Functions. Journal of Environmental Economics and Management, 59, 293-301. http://dx.doi.org/10.1016/j.jeem.2009.06.003
- Mishel, L. and Davis, A. (2014) CEO Pay Continues to Rise as Typical Workers are Paid Less. Issue Brief: Economic Policy Research Institute, No. 380.
- US Bureau of Economics Analysis (2015) National Income and Product Accounts Tables, Table 1.12. National Income by Type of Income. http://www.bea.gov/iTable/index.cfm
- US Bureau of Labor Statistics (2015) Current Population Survey, Labor Statistics from the Current Population Survey, Series LNS12000000. http://www.bls.gov/data/



