Theoretical Economics Letters
Vol.04 No.08(2014), Article ID:50725,5 pages
10.4236/tel.2014.48087
A General Criterion of Choice, with Discussion of Borch Paradox
Benito V. Frosini
Department of Statistical Sciences, Catholic University of Milan, Milano, Italy
Email: benito.frosini@unicatt.it
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 August 2014; revised 5 September 2014; accepted 2 October 2014
ABSTRACT
The author resumes a proposal by Frosini of a criterion of choice between probability prospects, which realizes a suggestion by Allais of taking account, beside the expected utility of the dispersion or variability of utilities. The suggested criterion is unidimensional, and is increasing with expected utility, and decreasing, for most people, who are risk averse, with the absolute deviation of utilities; a parameter multiplying this dispersion measure allows for risk-averse or risk-prone behaviour, according to its sign, and also for more or less departure from a certain prospect. This composite criterion shares practically all desirable conditions of rationality, and allows explaining all popular paradoxes in the literature about utility theory. Then the author deals with an apparent, but really false paradox, raised by Borch in connection with the representation of probability prospects in a Markowitz-type plot. This kind of analysis is modified from the traditional reference to points of type (mean, standard deviation) to the reference which replaces the standard deviation with the mean absolute deviation; no essential change is involved. The paper closes with some numerical examples which show the correctness of the suggested criterion, as compared to unaccettable conclusions of the expected utility approach.
Keywords:
Utility models, Paradoxes in expected utility, Risk aversion, Borch paradox, Mean-Variance

1. How to include dispersion of utilities into a unidimensional criterion of choice between prospects
For me it is an utmost and enduring surprise for the fact that many economists and statisticians persist in proposing and defending the so-called Expected Utility (EU) criterion in order to evaluate and compare probabilistic prospects, since the basic criticisms of Allais [1] and many other scholars, who pointed out the fundamental weakness of this theory, which simply disregards the dispersion, or spread, of the same prospects. This happens not withstanding the universal feeling, regularly applied to operational criteria that, between two prospects with equal utility expectation, the prospect with smaller dispersion must be preferred as less risky. The following sentence by Allais [1] clearly displays the problem and its possible solution: “L’erreur fondamentale de toute l’école américaine, c’est de négliger indirectement et inconsciemment, la dispersion des valeurs psycholo- giques”. This error is responsible for the many paradoxes discovered by Allais and other scholars [2] -[4] .
The usual and simplest applications of the choice problem are concerned with monetary outcomes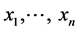 ,
,
associated with respective probabilities 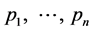
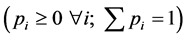 , and a utility
, and a utility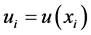 , formally
, formally
defined except for an affine transformation. Let 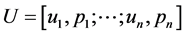 be the random variable which matches
be the random variable which matches
the utilities with their respective probabilities. Continuous distributions could be employed as well, with no essential modification of the theory. With reference to the case of  finite, von Neumann & Morgenstern [5] , starting from a simple set of axioms about economic behavior, obtained the following criterion in order to establish preferences among probability prospects
finite, von Neumann & Morgenstern [5] , starting from a simple set of axioms about economic behavior, obtained the following criterion in order to establish preferences among probability prospects
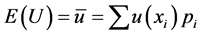 (1)
(1)
where 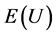 indicates the expected value (or arithmetic mean) of the prospect
indicates the expected value (or arithmetic mean) of the prospect . Among two or more prospects, one should choose the one which maximizes the expected utility [6] .
. Among two or more prospects, one should choose the one which maximizes the expected utility [6] .
As already stressed, complete exclusion from the criterion of choice of any reference to the dispersion of utility values weakens and restricts the possible (reasonable) applications of this criterion. Most scholars express the opinion that other characteristics (e.g. other moments) of the distribution  should enter the appreciation of a prospect, hence the comparison between prospects. As far as other moments (outside the mean) are concerned, the dispersion or variability of
should enter the appreciation of a prospect, hence the comparison between prospects. As far as other moments (outside the mean) are concerned, the dispersion or variability of 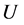 is evaluated of utmost importance; in the framework of Markowitz analysis [7] [8] directly applied to financial assets
is evaluated of utmost importance; in the framework of Markowitz analysis [7] [8] directly applied to financial assets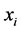 , the mean represents the average return, whereas variance (or its positive square root, the standard deviation) represents the risk; moreover “the mean-variance model may be improved by incorporating higher moments such as skewness and kurtosis” [9] .
, the mean represents the average return, whereas variance (or its positive square root, the standard deviation) represents the risk; moreover “the mean-variance model may be improved by incorporating higher moments such as skewness and kurtosis” [9] .
The mean-variance (MV) approach, following Markowitz and many other scholars, has the advantage of dealing directly with the portfolio values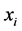 , not subjecting them to problematic utility transformations; how- ever, from the classical viewpoint of utility analysis, this fact entails rough approximations, and/or a neutral behaviour as far as utility is concerned. While most individuals are risk averse, using a linear utility can correctly be adopted in many cases of neutral, or almost neutral behaviour, such as the behaviour of firms. As deemed by Yaari [10] “in studying the behaviour of firms, linearity in payments may in fact be an appealing [and simplifying] feature”. As Yaari himself suggests [10] , and thoroughly shared by this author, “risk aversion and diminishing marginal utility of wealth, which are synonymous under expected utility theory, are horses of different colours”. The fact that practically all individuals have diminishing marginal utility of wealth has nothing to do with their attitude towards risk for any specified prospect; this contraposition mirrors one of the main weaknesses of expected utility theory. For a restatement of risk-neutral, risk-averse and risk-prone behaviour, according to this different approach, see Frosini [4] .
, not subjecting them to problematic utility transformations; how- ever, from the classical viewpoint of utility analysis, this fact entails rough approximations, and/or a neutral behaviour as far as utility is concerned. While most individuals are risk averse, using a linear utility can correctly be adopted in many cases of neutral, or almost neutral behaviour, such as the behaviour of firms. As deemed by Yaari [10] “in studying the behaviour of firms, linearity in payments may in fact be an appealing [and simplifying] feature”. As Yaari himself suggests [10] , and thoroughly shared by this author, “risk aversion and diminishing marginal utility of wealth, which are synonymous under expected utility theory, are horses of different colours”. The fact that practically all individuals have diminishing marginal utility of wealth has nothing to do with their attitude towards risk for any specified prospect; this contraposition mirrors one of the main weaknesses of expected utility theory. For a restatement of risk-neutral, risk-averse and risk-prone behaviour, according to this different approach, see Frosini [4] .
Starting from a utility function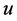 , the easiest way for constructing a unidimensional criterion which is decreasing with increasing risk taking, leads to a function increasing with expected utility and decreasing with a suitable measure of dispersion (or variability); mainly for reasons of simplicity, such a function should depend in a linear way on the expected utility and the chosen measure of dispersion. Frosini [4] [11] [12] suggested the simple criterion
, the easiest way for constructing a unidimensional criterion which is decreasing with increasing risk taking, leads to a function increasing with expected utility and decreasing with a suitable measure of dispersion (or variability); mainly for reasons of simplicity, such a function should depend in a linear way on the expected utility and the chosen measure of dispersion. Frosini [4] [11] [12] suggested the simple criterion
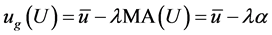 (2)
(2)
where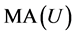 —also indicated with
—also indicated with 
and 



For any rational criterion of behaviour Frosini [4] assumes as absolutely requisite the (first) stochastic dominance, namely that the risky prospect 

tween the distribution function 






inequality for some
Frosini [4] shows that substitution of 




Frosini [4] shows that the criterion 

condition not particularly restrictive in applications). Subject to this same condition on

A reasonable subjective way towards operatively determining the value of 












counted by the factor










2. Some observations about the Borch paradox
An old paper by Borch [15] , concerned with an apparent paradox, proposed an example which seemed in radical contrast with the expected utility theory. This example, reported from Johnstone & Lindley [16] and extensively commented on this same paper, considered two prospects, related to two possible binary assets:
Asset 1 produces payoff 



Asset 2 produces payoff 



With a view to comment on this choice problem between the two assets within the Markowitz MV
(mean-variance) approach, let us summarize the two assets by means of the couples 

with the couples of type (mean, standard deviation). Given these summary statistics, it is possible to go back to the original probability prospects by means of the equations provided by Borch (also reported by Johnstone & Lindley, 2012, p. 6)




According to Markowitz MV approach, a prospect with couple 











from the first to the second prospect both the means and the standard deviations increase, thus showing a non- dominated problem, according to the MV approach. As a consequence, Borch derives that it is possible, for some individual, to be indifferent between the two prospects; however, the indifference condition 





Another opportune observation relates to the generality of the solutions (3)-(6), as far as the Markowitz 













Something like, however with some simplifications, happens by replacing the standard deviation 










Solving the system for the values







Of course, as already observed, translation by a value 










implies 


For the numerical illustration taken above from Johnstone and Lindley [16] , with values






Another numerical illustration, directly applied for a value
Prospect 1: 



Prospect 2: 



The relevant summary statistics are as follows:






Perhaps the most interesting examples are those showing a definite contrast between the 


Prospect 1: 



Prospect 2: 



The relevant summary statistics are:





result is
More generally, the comparison between 


any 
It is not a simple matter of calculations; practically all people would choose the prospect 


such as


3. Conclusion
The suggestion by Allais [1] that a criterion of choice between probability prospects should depend both on the expected utility associated with the prospects and on the dispersion of the same utilities around their means, has been made operative by Frosini [4] [12] by means of a simple linear function which depends on the expected utility and on the mean absolute deviation of the same utilities. Such a criterion satisfies the first stochastic dominance, the independence condition, and allows explaining the most popular paradoxes encountered in the applications of expected utility. This same criterion provides a simple way of discussing the so-called Borch paradox, recently focused by Johnstone and Lindley [16] .
References
- Allais, M. (1953) Le Comportement de l’Homme Rationnel Devant le Risque: Critique des Postulats et Axioms de l’Ecole Américaine. Econometrica, 21, 503-546. http://dx.doi.org/10.2307/1907921
- Ellsberg, D. (1961) Risk, Ambiguity, and the Savage Axioms. Quarterly Journal of Economics, 75, 643-669. http://dx.doi.org/10.2307/1884324
- Kahneman, D. and Tversky, A. (1979) Prospect Theory: An Analysis of Decision under Risk. Econometrica, 47, 263- 291. http://dx.doi.org/10.2307/1914185
- Frosini, B.V. (2012) Realistic Utility versus Game Utility: A Proposal for Dealing with the Spread of Uncertain Prospects. Statistica, 72, 3-22.
- Von Neumann, J. and Morgenstern, O. (1953) Theory of Games and Economic Behavior. 3rd Edition, Princeton University Press, Princeton.
- Lindley, D.V. (1985) Making Decisions. 2nd Edition, Wiley, London.
- Markowitz, H. (1952) The Utility of Wealth. Journal of Political Economy, 60, 151-158. http://dx.doi.org/10.1086/257177
- Markowitz, H. (1959) Portfolio Selection. Wiley, New York.
- Liu, L. (2004) A New Foundation for the Mean-Variance Analysis. European Journal of Operational Research, 158, 229-242.
- Yaari, M.E. (1987) The Dual Theory of Choice Under Risk. Econometrica, 55, 95-115. http://dx.doi.org/10.2307/1911158
- Frosini, B.V. (1997) The Evaluation of Risk Attitudes: A New Proposal. Statistica Applicata, 9, 435-458.
- Frosini, B.V. (2010) Realistic Utility versus Game Utility: A Proposal for Dealing with the Spread of Uncertain Prospects. Dipartimento di Scienze statistiche, Università Cattolica del Sacro Cuore, Serie E.P.N. 140. http://dipartimenti.unicatt.it/scienze statistiche_statistiche_2183.html
- Quiggin, J. (1982) A Theory of Anticipated Utility. Journal of Economic Behavior and Organization, 3, 323-343. http://dx.doi.org/10.1016/0167-2681(82)90008-7
- Quiggin, J. (1993) Generalized Expected Utility Theory. The Rank-Dependent Model, Kluwer, Boston. http://dx.doi.org/10.1007/978-94-011-2182-8
- Borch, K. (1968) Indifference Curves and Uncertainty. The Swedish Journal of Economics, 70, 19-24. http://dx.doi.org/10.2307/3438982
- Johnstone, D. and Lindley, D. (2012) Mean-Variance and Expected Utility: The Borch Paradox. Statistical Science, 28, 223-237. http://dx.doi.org/10.1214/12-STS408
- Levy, H. and Sarnat, M. (1969) A Note on Indifference Curves and Uncertainty. The Swedish Journal of Economics, 71, 206-208. http://dx.doi.org/10.2307/3439370




