Theoretical Economics Letters
Vol.4 No.3(2014), Article ID:44925,6 pages DOI:10.4236/tel.2014.43033
A Theoretical Model of Directional Volume on Acquirer Stock in Cash Mergers
Mark W. Zikiye1, Rebecca Abraham2, Charles Harrington2
1Zikiye Tactic Nutrition, Fort Lauderdale, USA
2Nova Southeastern University, Fort Lauderdale, USA
Email: verdigriebusiness@gmail.com, abraham@nova.edu, charlieh@nova.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 2 February 2014; revised 5 March 2014; accepted 20 March 2014
ABSTRACT
The acquisition of a target firm in a transaction financed by cash is a cash merger. Announcements of cash mergers release the positive signal that the acquirer possesses cash reserves. As stock prices rise, informed traders may obtain abnormal returns by purchasing call options, selling put options or purchasing stock. This paper constructs a theoretical model in which call buy volume forms the upper bound of the final stock price, put sell volume forms the lower bound of the final stock price and stock purchase volume reveals the final stock price.
Keywords:Option Volüme, Informed Trading, Cash Mergers, Signaling, Price Bounds

1. Introduction
The literature on informed trading as presented in Abraham, Harrington and Williams [1] , Easley, O’Hara and Srinivas [2] and Glosten and Milgrom, [3] provides empirical evidence that positive signals lead traders to anticipate stock price increases which in turn, stimulates call option purchases by options traders and purchases of stock by stock traders. In the Mitchell, Pulvino and Stafford [4] classification, such positive signals are released upon announcement of the acquisition of one firm by another in a transaction financed by cash. The financial markets observe that the acquiring firm has sufficient cash indicating financial stability. On the day prior to merger announcement, there is a price run up on the acquirer stock. Informed traders capitalize on the forthcoming price increase by purchasing stock or call options. Their gain is the difference between the final and initial stock prices for stock purchases, or the difference between the final stock price and call exercise price for call option purchases. For those who initially purchased put options to benefit from declining stock prices, losses may be limited by selling these put options. We propose a theoretical model which demonstrates that the upper bound of the stock price in any time interval on the day prior to merger announcement corresponds to call buy volume, the lower bound to put sell volume and the final stock price to stock purchase volume.
We extend the literature on informed trading and portfolio creation. Easley, O’Hara and Srinivas [2] observed that the stock and option markets were alternative venues for trading. We show that such venues can predict final stock prices if viewed as complementing each other. In other words, volumes traded in each market have unique characteristics that support each other in the determination of the final stock price. From a practical standpoint, the accurate forecast of future stock prices facilitates in the estimation of gains from trading. We derive the final stock price based on investor risk preferences. Traditional portfolio theory emphasizes the risk preferences of the risk-averse investor who finds optimal solutions on the mean-variance frontier which minimizes risk for varying levels of return [see Elton and Gruber [5] , for a review]. Our model includes both riskaversion and risk-taking with the recognition that the utility of wealth for the risk-taker lies on a concave utility function in which returns must be maximized regardless of risk.
2. The Theoretical Model
2.1. The Upper Bound
On the day prior to the acquisition of one firm by another using cash, the acquirer firm releases a positive signal that it has excess cash available for acquisitions. This signal stimulates informed traders to purchase call options in varying volumes. We define the existence of two traders. Trader 1 anticipates a modest increase in stock prices suggesting a modest gain of 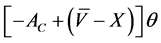 where
where
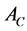 = price of the call option or call premium
= price of the call option or call premium
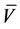 = the anticipated stock price corresponding to trade volume
= the anticipated stock price corresponding to trade volume
![]() = exercise price of the call option
= exercise price of the call option
![]() = the call option trade volume Trader 1 approaches the market maker who offers the call option at a range of ask prices. Trader 1 purchases
= the call option trade volume Trader 1 approaches the market maker who offers the call option at a range of ask prices. Trader 1 purchases ![]() options above the NBBO (National Best Bid and Offer). Trader 1’s gain will be
options above the NBBO (National Best Bid and Offer). Trader 1’s gain will be 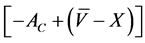
where ![]() = actual stock price corresponding to trade volume.
= actual stock price corresponding to trade volume.
In the second round of trading, the market maker increases the call premium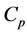 . Trader 1 will purchase more options in the hope that the anticipated stock price will be sufficiently high so that the gain on
. Trader 1 will purchase more options in the hope that the anticipated stock price will be sufficiently high so that the gain on  offsets the increase in the call premium,
offsets the increase in the call premium, . In the second round of trading, the total gain will be equal to
. In the second round of trading, the total gain will be equal to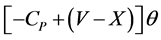 . At this point, given that the call premium will still increase, Trader 1 may feel that
. At this point, given that the call premium will still increase, Trader 1 may feel that 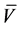 has reached the maximum and that any further increase in premium cannot be offset by the gain on
has reached the maximum and that any further increase in premium cannot be offset by the gain on . At this point, Trader 1 will cease trading. Trader 2 is a risk-taker who will continue to purchase call options in successive rounds believing that
. At this point, Trader 1 will cease trading. Trader 2 is a risk-taker who will continue to purchase call options in successive rounds believing that 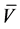 will be sufficiently higher than
will be sufficiently higher than ![]() to offset any increase in call premium. Finally Trader 2 stops trading. Given that Trader 2 is the last purchaser of call options within a certain time interval, the call buy volume of trader 2 in the final transaction will correspond to the upper bound of the call price.
to offset any increase in call premium. Finally Trader 2 stops trading. Given that Trader 2 is the last purchaser of call options within a certain time interval, the call buy volume of trader 2 in the final transaction will correspond to the upper bound of the call price.
Risk (r) is correlated to each anticipated stock price as determined by the number of options available for purchase. Risk is rationally and directly proportional to the anticipated stock price. L designates two different types of hypothetical funds, one being a conservative pension fund and the other being an aggressive hedge fund. Therefore the anticipated stock price may be represented as:
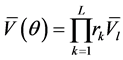 (1)
(1)
such that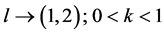 .
.
We first need to show that 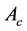 is reducible based on the assumption that a maximal or minimal value exists (accounting for inflections) for which the implicit price infinitesimally approaches the actual price with respect to some duration
is reducible based on the assumption that a maximal or minimal value exists (accounting for inflections) for which the implicit price infinitesimally approaches the actual price with respect to some duration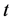 . The zeros of an ordinary differential equation will demonstrate elevations of noise around an inflection point. An inflection occurs when liquidity traders are factored into the pool of informed traders who, together, saturate the options market, therefore prices do not rise in a positive linear trajectory but rather in a curve between 0 and −0.75. The y component of the differential equation describes a separate function where the parts of the other two components f(0) and f(1) are interdependent. The inflections will be omitted in the pursuit of lending transparency to the upper boundary of stock price represented in the last trade of Trader 2.
. The zeros of an ordinary differential equation will demonstrate elevations of noise around an inflection point. An inflection occurs when liquidity traders are factored into the pool of informed traders who, together, saturate the options market, therefore prices do not rise in a positive linear trajectory but rather in a curve between 0 and −0.75. The y component of the differential equation describes a separate function where the parts of the other two components f(0) and f(1) are interdependent. The inflections will be omitted in the pursuit of lending transparency to the upper boundary of stock price represented in the last trade of Trader 2.
This can be done using a simple ordinary differential equation:
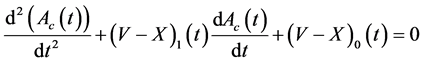 (2)
(2)
where  and
and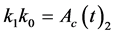 ;
; 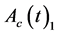 becomes a solution to the equation, we may follow the reduction order to generate:
becomes a solution to the equation, we may follow the reduction order to generate:
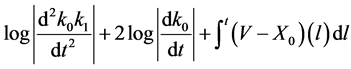 (3)
(3)
where ![]() is an integrable family of functions with the potential to be reduced to one solution. The data should explicitly comply with the integration of the above formula yielding:
is an integrable family of functions with the potential to be reduced to one solution. The data should explicitly comply with the integration of the above formula yielding:
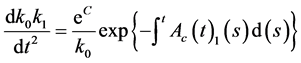 (4)
(4)
2.2. The Lower Bound
Trader 1 purchased put options prior to the cash merger announcement period. The day before the merger announcement, anticipated stock prices on the acquirer stock increase suggesting the unprofitability of a put buying strategy. In order to capitalize on rising stock prices the only course of action for Trader 1 is to sell put options. Trader 1 sells put options at the bid price in a market with rising actual and anticipated stock prices, ![]() and
and 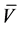 respectively. In successive rounds of trading, Trader 1 earns decreasing amounts of put premiums,
respectively. In successive rounds of trading, Trader 1 earns decreasing amounts of put premiums, 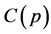 at progressively lower bid prices. In the final round of put selling, Trader 1 receives the minimum premium
at progressively lower bid prices. In the final round of put selling, Trader 1 receives the minimum premium 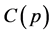 at
at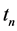 , the final period of trading. In the final round of put selling, Trader 1 receives the minimum premium
, the final period of trading. In the final round of put selling, Trader 1 receives the minimum premium 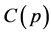 at time
at time 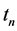 or
or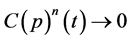 . The incremental time period between the penultimate and final rounds of trading
. The incremental time period between the penultimate and final rounds of trading 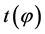 describes the achievement of the minimum put premium. The actual stock price corresponding to the minimum put premium is the lower bound.
describes the achievement of the minimum put premium. The actual stock price corresponding to the minimum put premium is the lower bound.
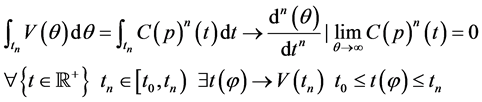 (5)
(5)
where
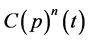 = put premium in the final round of trading, at time
= put premium in the final round of trading, at time 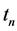
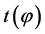 = incremental difference in time between
= incremental difference in time between 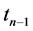 and
and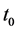 .
.
What is the final stock price? It is the price that is infinitesimally above the exercise price since it is at this price that the put buyer has no incentive to exercise the put option. At this stock price, the put seller sustains minimum loss which is offset by the minimum put premium. The lowest stock price above the exercise price may be described as the lower bound. The orthogonality of the Fourier-Bessel function describes the lower bound of 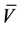 where
where
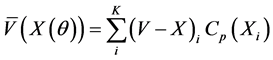 (6)
(6)
and
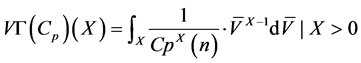
Let 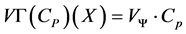 can then be rewritten such that transparency can be lent to
can then be rewritten such that transparency can be lent to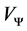 :
:
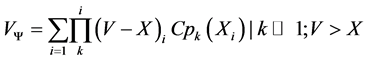 (7)
(7)
and the lower bound is ultimately defined as the solution of the Fourier-Bessel function.
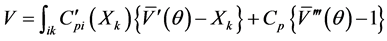 (8)
(8)
3. The Establishment of the Final Stock Price by the Risk-Averse Investor
Trading on the acquirer stock occurs in both the option and stock markets on the day prior to a cash merger announcement. At each round of trading in the stock market, traders purchase acquirer stock and market makers increase ask prices so that the stock is sold at increasingly higher prices. Stock volumes reflect trader expectations of the extent to which the actual stock price exceeds its forecast, or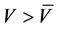 . Why does stock volume represent the final price while option volume represents the bounds? Stocks require a larger investment than options providing an incentive for risk-aversion in trading. Options buyers may seek higher returns by purchasing larger volumes of options while experiencing minimal loss in the event of non-exercise as option premiums are substantially lower than margined stock investments. As larger volumes of call options are purchased, the possibility that a highly optimistic trader exists becomes realistic. This trader’s call buy volume may approach the upper bound. Likewise, as larger volumes of put options are sold, the possibility exists that the least optimistic trader’s put sell volume may approach the lower bound.
. Why does stock volume represent the final price while option volume represents the bounds? Stocks require a larger investment than options providing an incentive for risk-aversion in trading. Options buyers may seek higher returns by purchasing larger volumes of options while experiencing minimal loss in the event of non-exercise as option premiums are substantially lower than margined stock investments. As larger volumes of call options are purchased, the possibility that a highly optimistic trader exists becomes realistic. This trader’s call buy volume may approach the upper bound. Likewise, as larger volumes of put options are sold, the possibility exists that the least optimistic trader’s put sell volume may approach the lower bound.
Risk-averse investor behavior has formed the bases of the Markowitz [6] model, the Capital Asset Pricing model [7] and the Sharp-Lintner [8] model. The implicit assumption of these models is that diversified portfolios are preferred in that they reduce or even theoretically eliminate portfolio risk. In this section, we draw upon the Markowitz [6] model to specify the establishment of the final stock price based upon Trader 1’s aversion to risk. In the next section, we demonstrate investor choices with risk taking as modeled by Trader 2. Trader 1’s actions may approximate those of a risk-averse investor. Such an investor will create portfolios of negatively correlated securities whose movements are in opposite directions so that the standard deviation of the portfolio may be minimized through diversification. This investor ceases trading when he or she perceives that additional return may only be obtained by exceeding his or her threshold of risk. Markowitz [6] identified a collection of optimal portfolios for risk-averse investors termed the mean-variance efficiency frontier. Therefore, the maximum stock price, V, for Trader 1 is the critical point on the mean-variance efficiency frontier at which the standard deviation of returns of the optimal portfolio of risky assets is minimized for a particular return. Given the heterogeneity of expectations among risk-averse traders (Trader 1 is one individual within the universe of risk-averse traders) equity trading volume may cluster at different stock prices, leading to a range of final stock prices. Merton [9] specified the return and standard deviation on a two-asset portfolio. Security i establishes the threshold return for the portfolio so that if a trader wishes to earn higher returns he or she would have to invest in the riskier security j. To achieve the objective of minimizing risk, the portfolio containing securities i and j must be diversified with respect to the sum of all portfolios on the efficient frontier. Merton’s [9] derivation of expected return and risk of the optimal portfolio yields.
Expected return of optimal portfolio containing security
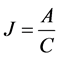 (9)
(9)
Standard deviation (risk) of the optimal portfolio containing security
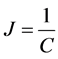 (10)
(10)
where
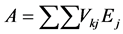 (11)
(11)
and
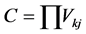 (12)
(12)
such that 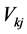 = covariance risk of k portfolios and security j and
= covariance risk of k portfolios and security j and 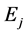 = expected return of security j.
= expected return of security j.
In the context of this paper, security j may be an acquirer stock in a cash merger. The stock is expected to increase in price on the day before the merger announcement. The stock increases the return and risk on the risk-averse investor’s portfolio. The investor minimizes the additional risk by adjusting the proportion of the portfolio invested in security j, purchasing limited amounts of j, computing the risk of the portfolio in each round of trading, finally ceasing trading upon achieving the risk level appropriate to his or her risk preference. The stock price in the final round of trading is the final stock price.
In order to obtain the final stock price, we rewrite the expected return on the optimal portfolio containing security j, i.e. Equation (13),
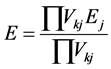 (13)
(13)
The final stock price of security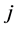 , the acquirer stock in a cash merger is
, the acquirer stock in a cash merger is ![]() or the stock price in the final round of trading at time
or the stock price in the final round of trading at time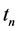 . The stock price of security j in the penultimate round of trading at time
. The stock price of security j in the penultimate round of trading at time 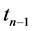 is
is![]() . Substituting in Equation (13),
. Substituting in Equation (13),
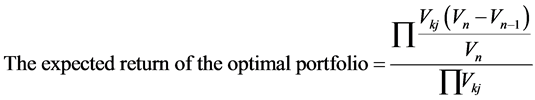 (14)
(14)
The solution of Equation (14) yields the final stock price,![]() .
.
4. The Establishment of the Final Stock Price by the Risk-Taker
Although the aforementioned literature emphasized the actions of the risk-averse investor, it may be possible to envision the existence of alternative investor motivations. The risk taker pursues higher returns regardless of risk. Such an individual has a concave utility function with the value of higher returns continuously increasing with risk. The optimal portfolio may consist of a few positively or negatively correlated securities with high return and potentially high risk. Given the broad array of such combinations of securities, there may be varying stock prices corresponding to the risk tolerance of each risk-taker. There may be little incentive to pursue the goal of diversification presumably as diversification is a risk-reduction strategy. On the day prior to cash merger announcement, the risk-taker, Trader 2, continues to purchase acquirer stock long after the risk-averse trader has ceased trading with the expectation of increasing expected returns as 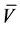 converges to a higher value of
converges to a higher value of![]() . In each round of trading, Trader 2 purchases stock, the market maker increases the ask price followed by further purchase of stock. Trading only ceases when Trader 2 feels that the entire price run up on the stock has occurred and that no further gain from purchasing stock can accrue in the stock market. Alternatively, institutional constraints such as reluctance on the part of the employer to commit more funds to investment in a particular risky portfolio may halt trading. Therefore, Trader 2 remains in the market long after Trader 1 has suspended trading.
. In each round of trading, Trader 2 purchases stock, the market maker increases the ask price followed by further purchase of stock. Trading only ceases when Trader 2 feels that the entire price run up on the stock has occurred and that no further gain from purchasing stock can accrue in the stock market. Alternatively, institutional constraints such as reluctance on the part of the employer to commit more funds to investment in a particular risky portfolio may halt trading. Therefore, Trader 2 remains in the market long after Trader 1 has suspended trading.
We employ a stochastic programming model to state the objective function and constraints for the risk-taker. In empirical tests, multiperiod stochastic programming models for portfolio selection have outperformed value-at-risk models [see Puelz, [10] , for a review]. Such models account for flat-tailed leptokurtic distributions of stock prices, thereby relaxing the assumption of normality [Hiller and Eckstein, [11] ; Mulvey and Vladimirou, [12] ; Zenios, [13] . Thus, they are particularly applicable in our context with trading at extremely high values of stock prices. The utility function is to create wealth by maximizing portfolio returns in a portfolio of high return-high risk stock with each additional stock being added to the portfolio if it meets a threshold rate of return.
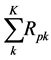 (15)
(15)
ST
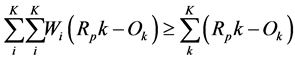 (16)
(16)
Cash flow:
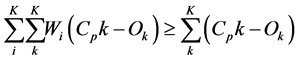 (17)
(17)
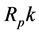 = total return on the portfolio
= total return on the portfolio
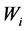 = weight of each asset in portfolio
= weight of each asset in portfolio
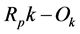 = return on the portfolio that excludes the acquirer stock
= return on the portfolio that excludes the acquirer stock
![]() = last round of trading
= last round of trading
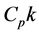 = total dividends on the portfolio
= total dividends on the portfolio
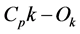 = total dividends on portfolio that excludes the acquirer stock A branch and bound solution procedure may be employed. In the first round of trading, the return and dividends on a portfolio that excludes the acquirer stock is measured. This is the current value of the objective function. Then, acquirer stock, o, is purchased at the initial ask price. The return and dividends of this portfolio form a branch. The total stock price appreciation and dividends before and after the addition of stock o are measured, with the portfolio containing stock o only remaining as an active branch as long as its stock price appreciation and dividends exceeds that of the portfolio that did not contain stock o. In the final round of trading, the return and dividends on the active branch equals the stock price appreciation and dividends on the active branch resulting in suspension of trading. The stock price in the final round of trading is the final stock price.
= total dividends on portfolio that excludes the acquirer stock A branch and bound solution procedure may be employed. In the first round of trading, the return and dividends on a portfolio that excludes the acquirer stock is measured. This is the current value of the objective function. Then, acquirer stock, o, is purchased at the initial ask price. The return and dividends of this portfolio form a branch. The total stock price appreciation and dividends before and after the addition of stock o are measured, with the portfolio containing stock o only remaining as an active branch as long as its stock price appreciation and dividends exceeds that of the portfolio that did not contain stock o. In the final round of trading, the return and dividends on the active branch equals the stock price appreciation and dividends on the active branch resulting in suspension of trading. The stock price in the final round of trading is the final stock price.
This paper has developed a theoretical model in which options and stock act in conjunction in the establishment of stock prices. Thus, we view the option and stock markets not only as alternative venues for trading, but as components of a single trading system with different functions. We extend the literature that examines the establishment of stock prices by the risk-averse investor to include risk-takers. Future research must examine if the exercise price forms an artificial bound that conflicts with the true upper and lower bounds identified in this paper. This model may be adapted to other informed events releasing positive signals. They include dividend announcements and positive earnings surprises.
References
- Abraham, R., Harrington, C.W. and Williams, A.A. (2011) Multimarket Trading at Merger Announcement and Completion. Journal of Derivatives and Hedge Funds, 17, 186-197.
- Easley, D.O., O’Hara, M. and Srinivas, P. (1998) Option Volume and Stock Prices: Evidence on Where Informed Traders Trade. Journal of Finance, 53, 431-465. http://dx.doi.org/10.1111/0022-1082.194060
- Glosten, L.R. and Milgrom, P.R. (1985) Bid, Ask and Transaction Prices in a Specialist Market with Heterogeneously Informed Traders. Journal of Finance, 14, 71-100.
- Mitchell, M., Pulvino, T. and Stafford, E. (2004) Price Pressure around Mergers. Journal of Finance, 59, 31-63. http://dx.doi.org/10.1111/j.1540-6261.2004.00626.x
- Elton, E.J. and Gruber, M.J. (1997). Modern Portfolio Theory, 1950 to Date. Journal of Banking and Finance, 21, 1743-1759. http://dx.doi.org/10.1016/S0378-4266(97)00048-4
- Markowitz, H. (1952) The Utility of Wealth. Journal of Political Economy, 60, 151-158. http://dx.doi.org/10.1086/257177
- Sharpe, W.F. (1964) Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Journal of Finance, 19, 425-442.
- Lintner, J. (1965) The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets. Review of Economics and Statistics, 47, 13-37. http://dx.doi.org/10.2307/1924119
- Merton, R.C. (1972) An Analytic Derivation of the Efficient Portfolio Frontier. Journal of Financial and Quantitative Analysis, 7, 1851-1872. http://dx.doi.org/10.2307/2329621
- Puelz, A.V. (2000) A Stochastic Convergence Model for Portfolio Selection. Operations Research, 50, 462-476. http://dx.doi.org/10.1287/opre.50.3.462.7738
- Hiller, R.S. and Erickson, J. (1993) Stochastic Dedication: Designing Fixed Income Portfolios Using Massively Parallel Benders Decomposition. Management Science, 39, 1422-1438. http://dx.doi.org/10.1287/mnsc.39.11.1422
- Mulvey, J.M. and Vladimirou, R.J. (1992) Stochastic Network Programming for Financial Planning Problems. Management Science, 38, 1642-1664. http://dx.doi.org/10.1287/mnsc.38.11.1642
- Zenios, R.A. (1991) Massively Parallel Computation for Financial Planning Under Uncertainty. In: Mersirov, J.D., Ed., Very Large Scale Computing in the 21st Century, SIAM, Philadelphia, 273-294.

