Theoretical Economics Letters
Vol. 2 No. 5 (2012) , Article ID: 25803 , 6 pages DOI:10.4236/tel.2012.25086
The Multivariate Rational Addiction Model
Department of Agricultural & Resource Economics, North Carolina State University, Raleigh, USA
Email: michaelwhlgnnt@gmail.com
Received July 26, 2012; revised August 27, 2012; accepted September 29, 2012
Keywords: Rational Addiction Model; Dynamic Frisch Demand Functions; Dynamic Consumer Demand; Habit Formation
ABSTRACT
This paper generalizes the model of Becker, Grossman, and Murphy (1994) to the multivariate case. The multivariate model generates Frisch demand functions where current consumption is related to prices of all goods, and lagged and future consumption of all goods. The theoretical restrictions are that current price effects (holding lagged and future consumption constant) are negative definite, and lagged and future consumption are proportional to one another, the proportionality factor being the consumer’s discount rate. The conditions for dynamic stability are derived, and the solution to the matrix difference equation is derived. General formulas for multivariate Frisch price elasticities with respect to different lengths of time are also derived. Finally, alternative econometric specifications are derived, showing how theoretical restrictions can be imposed to test the theory and to reduce the number of estimable parameters. It is also shown how the model can be modified to account for different discount rates by commodity when estimating the model using aggregate data.
1. Introduction
The workhorse of empirical analysis of dynamic demand is the rational addiction model of Becker, Grossman, and Murphy [1]. This model has proved useful in estimating short-run and long-run demand elasticities, but it only allows for one commodity and one composite good. To the author’s knowledge, no one has rigorously formulated and analyzed the multivariate counterpart to the single-equation model. Bask and Melkersson [2] and Pierani and Tiezzi [3] extend the rational addiction model to two goods (and the composite good), but do not analyze the restrictions imposed by theory or derive the dynamic properties of the model. The purpose of this paper is to present the multivariate addiction model and analyze the restrictions imposed by theory as well as the dynamic properties of the solution to the matrix difference equation.
2. The General Rational Addiction Model
The simple rational addiction model is extended by specifying that the consumer’s utility function for period t is given by the strictly concave, twice-differentiable function
 (1)
(1)
where  is an n-vector of quantities of goods consumed in time period t,
is an n-vector of quantities of goods consumed in time period t, 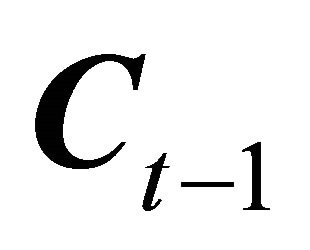 is an n-vector of quantities of goods consumed in the previous time period
is an n-vector of quantities of goods consumed in the previous time period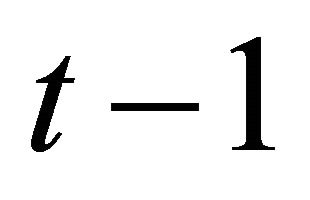 , and
, and  is the quantity of a composite good at time t representing consumption of all other goods1. We shall assume that the individual consumer maximizes the utility of life-time consumption with utility discounted at rate
is the quantity of a composite good at time t representing consumption of all other goods1. We shall assume that the individual consumer maximizes the utility of life-time consumption with utility discounted at rate . With
. With  the vector of prices associated with
the vector of prices associated with , the consumer’s problem is to maximize
, the consumer’s problem is to maximize
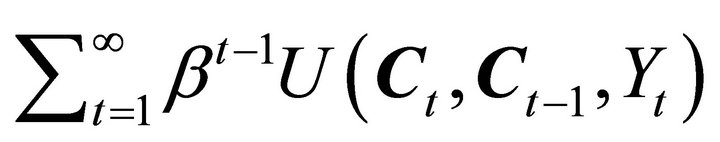 (2)
(2)
subject to the intertemporal budget constraint
 (3)
(3)
where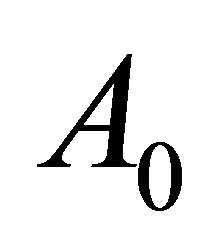 is initial wealth and with initial conditions
is initial wealth and with initial conditions  2.
2.
The first-order conditions (F.O.C.) for utility maximization are
 (4a)
(4a)
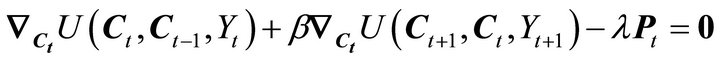 (4b)
(4b)
where is the marginal utility of wealth and
is the marginal utility of wealth and  is the gradient vector with respect to
is the gradient vector with respect to . Equation (4a), as in [1], is the condition that the marginal utility of the composite good equals the marginal utility of wealth. Equation (4b) generalize the univariate case to the multivariate case where the marginal utility of current consumption of each good plus the discounted value of next period’s marginal utility of consumption equals the marginal utility of wealth times the price of the good. As in [1], the model allows for both harmful addiction
. Equation (4a), as in [1], is the condition that the marginal utility of the composite good equals the marginal utility of wealth. Equation (4b) generalize the univariate case to the multivariate case where the marginal utility of current consumption of each good plus the discounted value of next period’s marginal utility of consumption equals the marginal utility of wealth times the price of the good. As in [1], the model allows for both harmful addiction
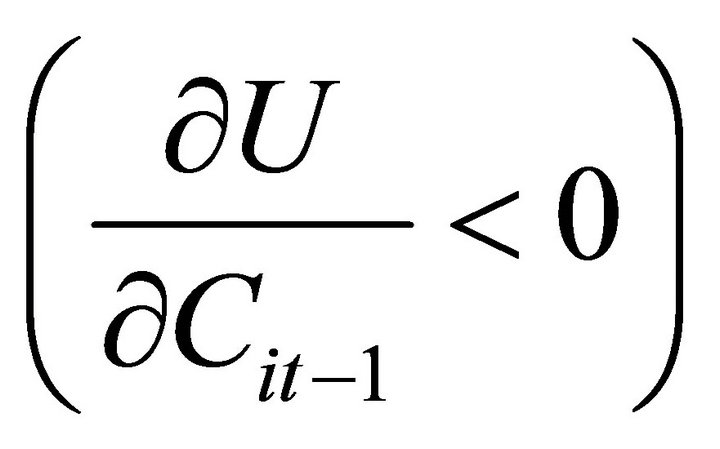
and beneficial addiction 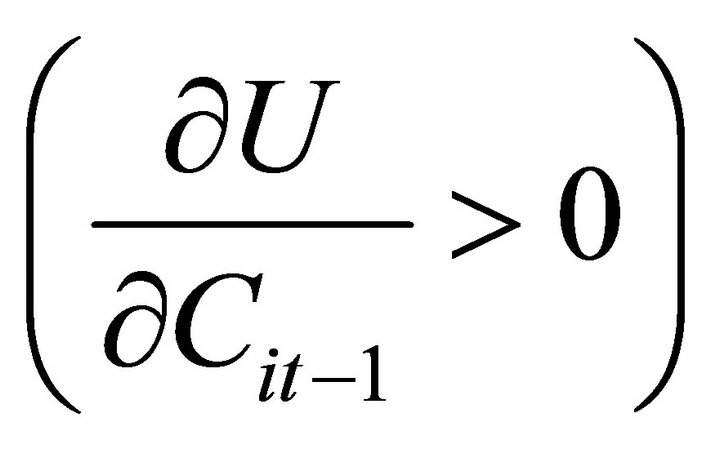
If the consumer takes the marginal utility of wealth constant in formulating decisions for the first-period of his planning horizon, then we can derive marginal utility of wealth constant (Frisch) demand functions showing how current period consumption responds to past, present, and future (expected) prices3. In keeping with a common assumption made when modeling intertermporal demand behavior [4], I assume that the marginal utility of consumption of good i is independent of the quantity of consumption of good j (j ≠ i) of goods consumed in the previous time period
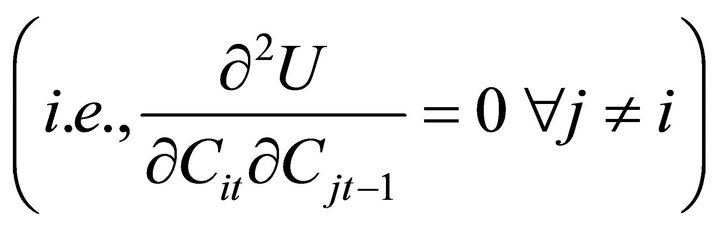 4
4
I also assume that the marginal utility of , while dependent on
, while dependent on  is independent of
is independent of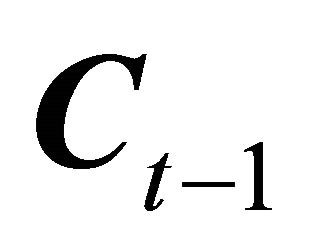 5.
5.
Assume that the current period utility function can be approximated by a quadratic function so that the F.O.C. can be expressed as6
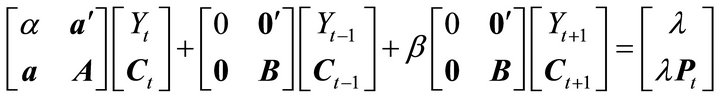 (5)
(5)
Where 
and .
.
The vector 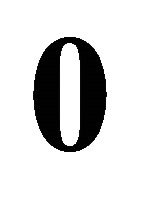 is an n-vector of zeros and
is an n-vector of zeros and 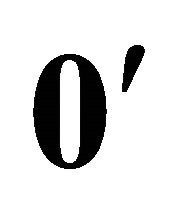 is its transpose. The matrix pre-multiplying
is its transpose. The matrix pre-multiplying
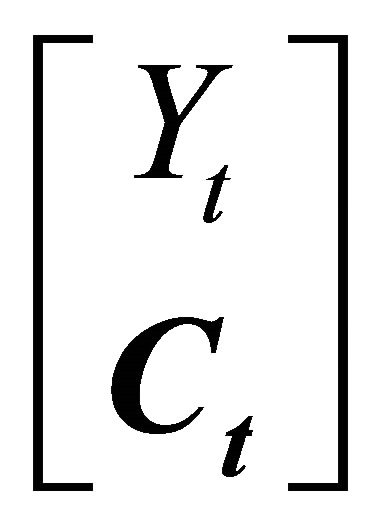
is negative definite. Therefore, its inverse exists and has the following partitioned form:
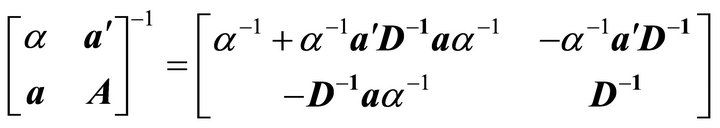 (6)
(6)
where  is a negative definite matrix, because
is a negative definite matrix, because  is the second principal submatrix of
is the second principal submatrix of
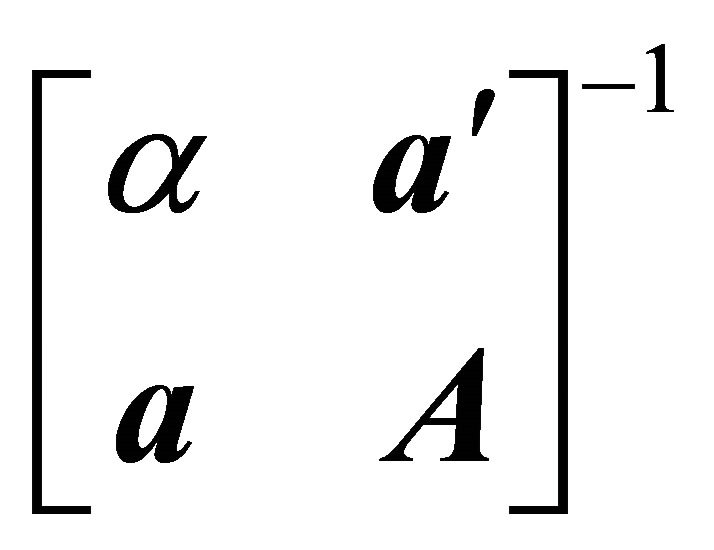
which is negative definite. Given the partitioned inverse (6), the solution to  is
is
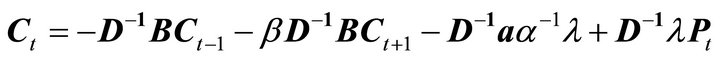 (7)
(7)
In contrast to the univariate rational addiction model, consumption of good i in the current period is related to lagged consumption of good i, as well as lagged values of all other consumption goods. Moreover, current consumption of good i is related to consumption of all consumption goods in period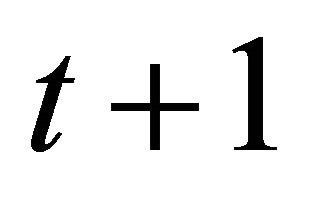 . Because
. Because 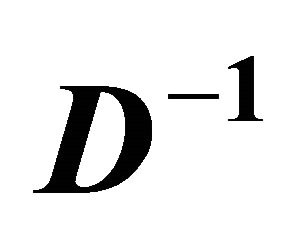 is negative definite, current period price effects (holding future consumption constant) are negative definite. When
is negative definite, current period price effects (holding future consumption constant) are negative definite. When  is diagonal
is diagonal

3. Stability and General Solution of Matrix Difference Equation
Proposition
When  is bounded, the general solution to the matrix difference Equation (7) can be expressed as
is bounded, the general solution to the matrix difference Equation (7) can be expressed as
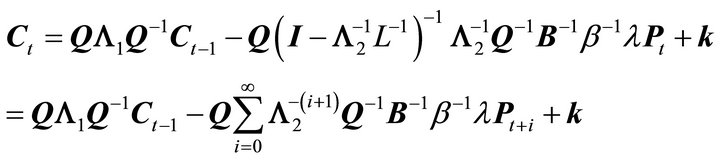
where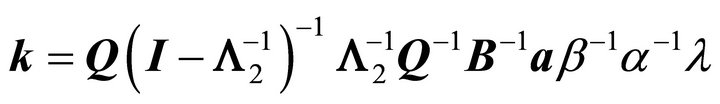 ,
, is the diagonal matrix of positive, real eigenvalues which lie within the unit circle, and
is the diagonal matrix of positive, real eigenvalues which lie within the unit circle, and  is the diagonal matrix of positive, real eigenvalues which lie outside the unit circle.
is the diagonal matrix of positive, real eigenvalues which lie outside the unit circle.
Proof. Rewrite the system of Equation (7) in difference equation form using the lag operator to obtain7:
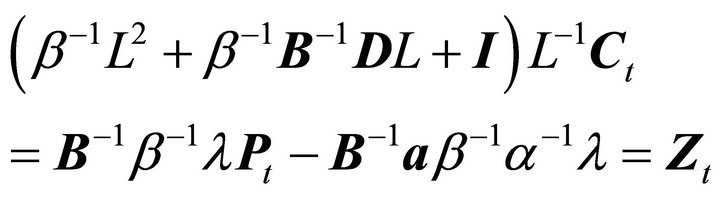 (8)
(8)
When 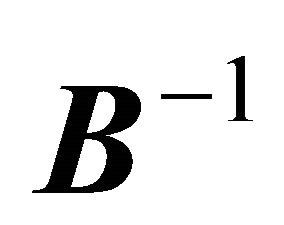 is a diagonal matrix with positive elements,
is a diagonal matrix with positive elements,  is positive definite and symmetric because
is positive definite and symmetric because  is symmetric negative definite8. Therefore, there exists an orthogonal matrix
is symmetric negative definite8. Therefore, there exists an orthogonal matrix  such that
such that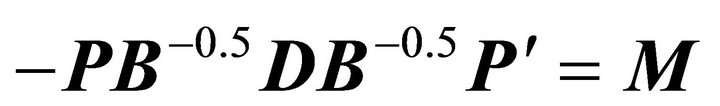 , a diagonal matrix with all distinct, positive elements. Define the transformation
, a diagonal matrix with all distinct, positive elements. Define the transformation 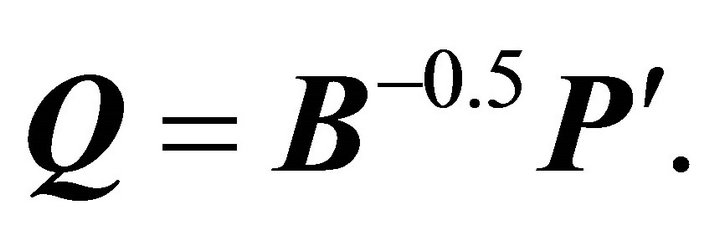 Then
Then 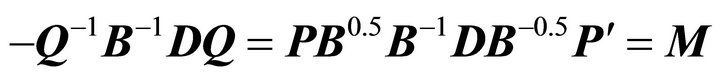 . Therefore,
. Therefore,  and
and 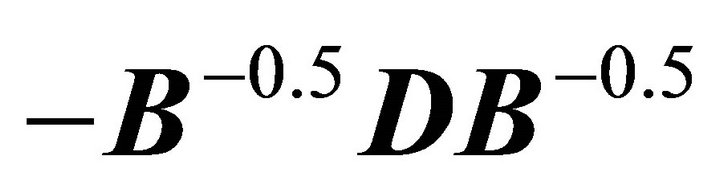 are similar matrices [5]. Multiply both sides of (8) by
are similar matrices [5]. Multiply both sides of (8) by 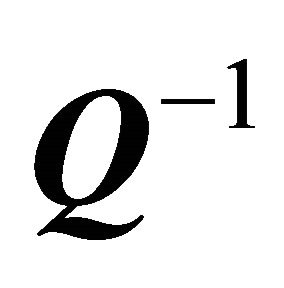 to obtain
to obtain

or

because . Define
. Define  and
and . Then the above equation can be written as
. Then the above equation can be written as
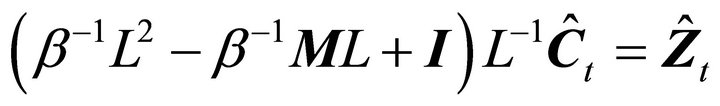 (9)
(9)
The matrix polynomial on the left-hand side of (9) can be written as
 (10)
(10)
The right-hand side of Equation (10) implies that
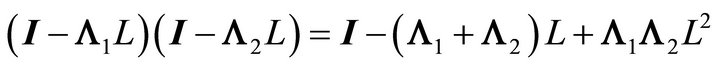 (11)
(11)
where 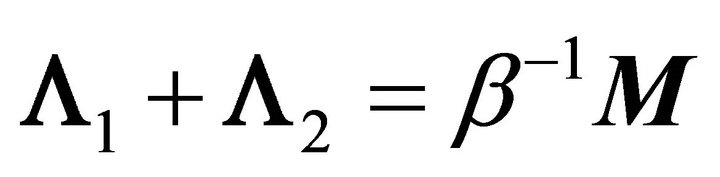 and
and . The matrix polynomial in (11) is a set of single, second-order difference equations of the form
. The matrix polynomial in (11) is a set of single, second-order difference equations of the form
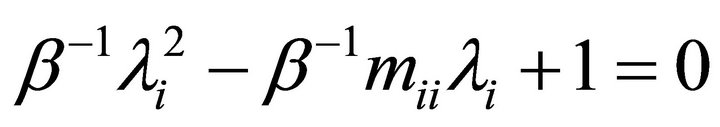
This matrix polynomial consists of individual characteristic equations of the form
 . (12)
. (12)
Because the diagonal elements of  are real, we know that
are real, we know that 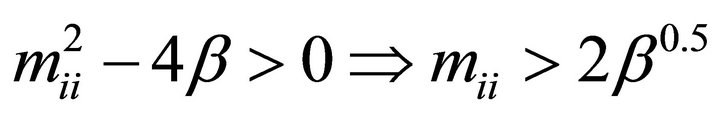 and both roots are real and distinct. For stability,
and both roots are real and distinct. For stability, 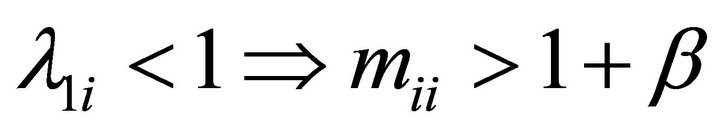 and
and  9. By the relationship among roots,
9. By the relationship among roots, 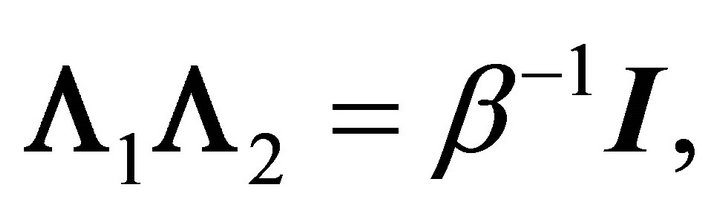 this means
this means 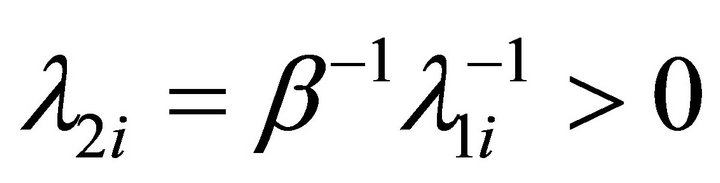 when
when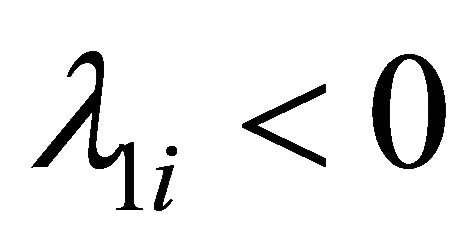 .
.
The matrix  can be expressed as
can be expressed as  . Noting also that
. Noting also that  , the matrix Equation (9) can be written as
, the matrix Equation (9) can be written as
 (13)
(13)
Multiplying both sides by the inverse of  yields
yields
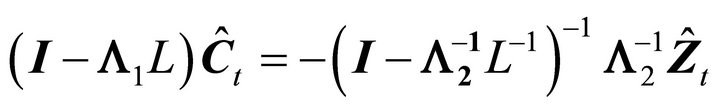
Substituting back in terms of  and
and , and multiplying both sides by
, and multiplying both sides by  we obtain
we obtain
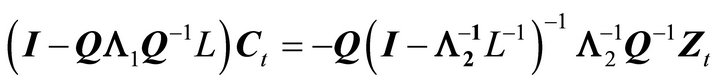 which immediately leads to the desired result.
which immediately leads to the desired result.
4. Elasticities
Short-run and long-run elasticities can be derived from the structural parameter estimates. From the above Proposition we see that the price derivatives of the dynamic demand functions are
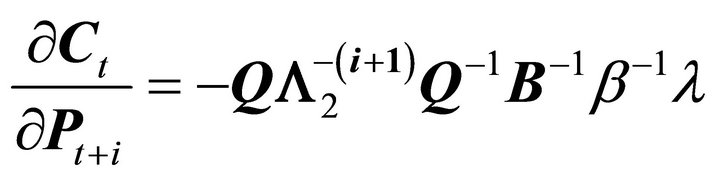 (14a)
(14a)
holding all past prices constant for a temporary price change. For an expected permanent future price change
 (14b)
(14b)
Finally, the long-run price effects are
 (14c)
(14c)
5. An Example
As an example to illustrate the method of calculating the solution to the matrix difference equation and formulas for elasticities consider the two good case which might correspond to two addictive goods such as alcohol and tobacco. Specify the matrices  and
and  as follows
as follows
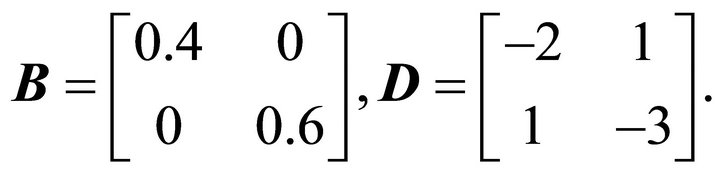
Assuming a discount rate of , the matrices of eigenvalues associated with
, the matrices of eigenvalues associated with  are
are

The matrix consisting of the two eigenvectors associated with the set of eigenvalue is as follows
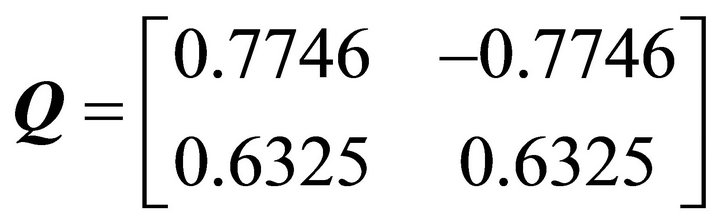
Given these numbers, the solution to the matrix difference equation shown in Proposition is
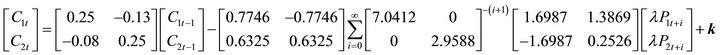
The matrices of price elasticities shown in Equations (14a)-(14c) are as follows:
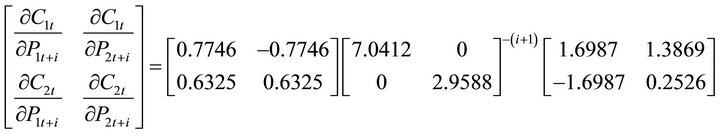 (14a’)
(14a’)
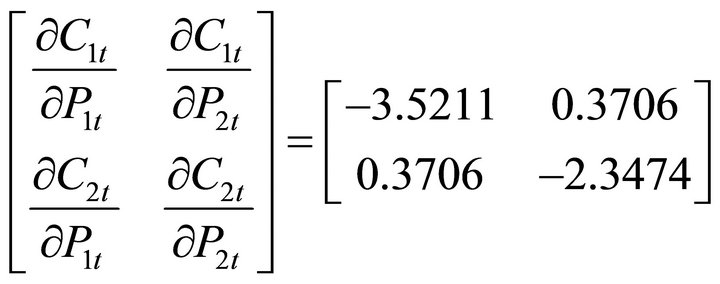 (14b’)
(14b’)
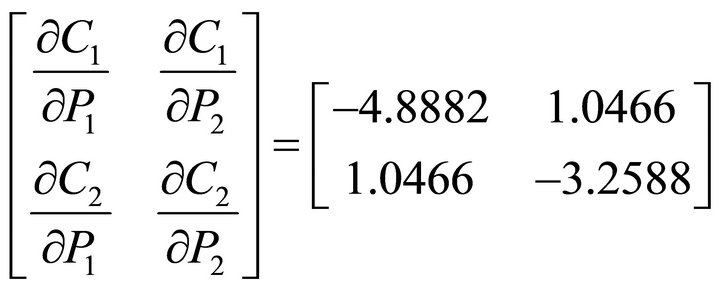 (14c’)
(14c’)
This example shows that the solution to the matrix difference equation is stable because the matrix  consists of positive real roots all within the unit circle, and the matrix
consists of positive real roots all within the unit circle, and the matrix 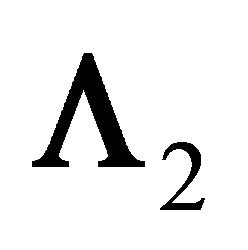 consists of positive real roots all outside the unit circle. The solution also shows that both goods are interrelated in consumption through lagged quantities and current and future prices. Note also that the matrices of price effects as shown in (14a’)-(14c’) indicate that all own-price effects are negative, and all cross-price effects are symmetric and positive. This numerical illustration indicates that we should expect changes in current and future price effects to exhibit complementary effects when both goods exhibit habit formation. In addition, all long-run price effects (in absolute value) should be larger than short-run price effects.
consists of positive real roots all outside the unit circle. The solution also shows that both goods are interrelated in consumption through lagged quantities and current and future prices. Note also that the matrices of price effects as shown in (14a’)-(14c’) indicate that all own-price effects are negative, and all cross-price effects are symmetric and positive. This numerical illustration indicates that we should expect changes in current and future price effects to exhibit complementary effects when both goods exhibit habit formation. In addition, all long-run price effects (in absolute value) should be larger than short-run price effects.
6. Econometric Implications
There is more than one approach to take for quantifying rational addiction behavior. The simplest approach would be to start with the F.O.C. from Equation (5), after eliminating  from the set of equations related to
from the set of equations related to , to obtain
, to obtain
 (15)
(15)
where  is a vector of constants,
is a vector of constants,  is income, and
is income, and  is a vector of disturbance terms10. The advantage of this specification is that it simplifies imposing and testing for the theoretical restrictions. The testable restrictions are that the matrix
is a vector of disturbance terms10. The advantage of this specification is that it simplifies imposing and testing for the theoretical restrictions. The testable restrictions are that the matrix , which represents intra-period substitution among the individual consumption goods, is symmetric and negative definite. Thus, the symmetry restriction
, which represents intra-period substitution among the individual consumption goods, is symmetric and negative definite. Thus, the symmetry restriction 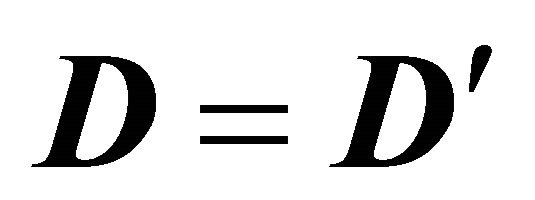 could be imposed linearly and tested. Because
could be imposed linearly and tested. Because  is a matrix of constants, one could also impose negative definiteness on the contemporary substitution matrix using one of the several methods available in the literature (e.g., [7]). The other restriction that one may wish to impose is
is a matrix of constants, one could also impose negative definiteness on the contemporary substitution matrix using one of the several methods available in the literature (e.g., [7]). The other restriction that one may wish to impose is . With diagonal matrices, this means the restriction is
. With diagonal matrices, this means the restriction is  for each equation.
for each equation.
From an econometric point of view, it is straight forward to estimate the model using generalized method of moments by finding instruments such that the orthogonality condition  holds, where
holds, where 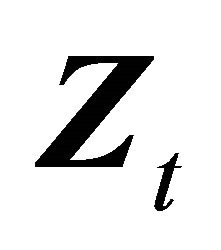 is a vector of instrumental variables. In this case, as in [1], we could use current, lagged, and futures prices as instruments, in addition to income. If it is not reasonable to assume that consumers know future prices with high probability then we could use current and enough lagged prices sufficient enough to identify the parameters of the F.O.C.
is a vector of instrumental variables. In this case, as in [1], we could use current, lagged, and futures prices as instruments, in addition to income. If it is not reasonable to assume that consumers know future prices with high probability then we could use current and enough lagged prices sufficient enough to identify the parameters of the F.O.C.
The few attempts to extend the rational addiction model to more than one good ([2], [3]) specify the model as follows
 (16)
(16)
where 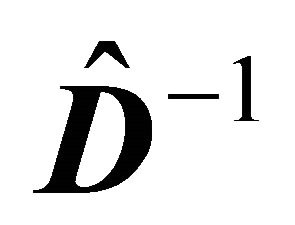 is the diagonal matrix whose diagonal elements are
is the diagonal matrix whose diagonal elements are  so that the ith equation can be written as
so that the ith equation can be written as
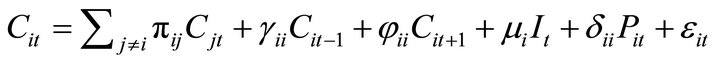 (17)
(17)
In light of (16), the symmetry constraint, which is now nonlinear, would be imposed as follows:
 .
.
The parameter  could then be estimated separately and an estimated value of
could then be estimated separately and an estimated value of  obtained by dividing the estimate of
obtained by dividing the estimate of  by
by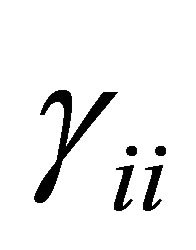 .
.
The other approach to estimation is what [2] and [3] call the reduced-form approach and is indicated by Equation (7), generalized below as follows
 (18)
(18)
where

This set of equations like (16) has nonlinear restricttions. Equation (18), however, is consistent with the view that the consumer chooses quantities of all goods in the current period simultaneously. It is notable that neither [2] or [3] attempted to utilize these restrictions from theory implied by Equation (16) or Equation (18) in their empirical work.
We typically do not have the luxury to work with panel data at the individual household level. Therefore, it is clear that the estimates of the discount factor may differ from one commodity to another. This is particularly true with aggregate data as in [3], where it is shown that the discount rates for alcohol and tobacco are quite different. To see why estimates based on aggregate data could produce divergent estimates by commodity, note that average consumption of good i, when the discount rate is allowed to be different for each consumer, can be written as follows (over-bars denote simple averages over the total population of consumers):
 (19)
(19)
where ,
,
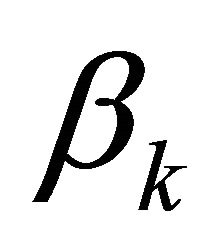 is the discount factor for consumer k,
is the discount factor for consumer k,  is consumption of consumer k for good i at time t+1, and
is consumption of consumer k for good i at time t+1, and  is aggregate consumption of good i. The significant feature of Equation (19) is that the aggregate discount factor
is aggregate consumption of good i. The significant feature of Equation (19) is that the aggregate discount factor  is a weighted average of discount factors, each weighted by consumer k’s consumption relative to total consumption. Clearly these weights need not be the same for all consumers. For example, even with the same utility function, a consumer with a higher income could consume a different mix of all consumption goods than a consumer with a lower income. With different discount rates, the average discount rate
is a weighted average of discount factors, each weighted by consumer k’s consumption relative to total consumption. Clearly these weights need not be the same for all consumers. For example, even with the same utility function, a consumer with a higher income could consume a different mix of all consumption goods than a consumer with a lower income. With different discount rates, the average discount rate  could be different for different goods. Therefore, for aggregate data, Equation (19) should be modified as follows:
could be different for different goods. Therefore, for aggregate data, Equation (19) should be modified as follows:
 (20)
(20)
where  is indexed by the particular good consumed. This means different discount rates can be accommodated by the model, while preserving symmetry and negative definiteness in own quantity effects. Note that all the above results still hold when
is indexed by the particular good consumed. This means different discount rates can be accommodated by the model, while preserving symmetry and negative definiteness in own quantity effects. Note that all the above results still hold when 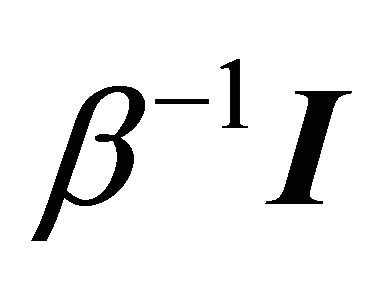 is replaced with
is replaced with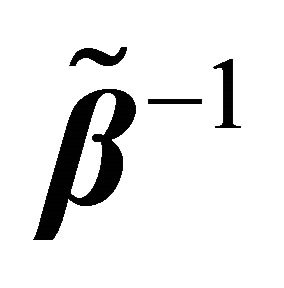 , where
, where  is the diagonal matrix with diagonal elements
is the diagonal matrix with diagonal elements 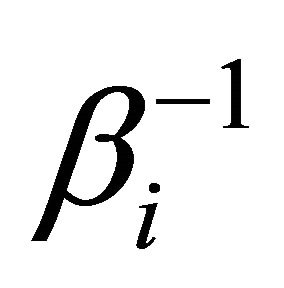 11.
11.
7. Concluding Remarks
This paper formulates and analyzes the multivariate version of the rational addiction model of Becker, Goldman, and Murphy [1]. The multivariate counterpart to the univariate model is that consumption of a specific good in the current period depends on prices of all goods, lagged consumption of all goods, and future consumption of all goods. The theoretical restrictions are that current price effects are negative definite, holding lagged and future consumption constant, and current and past consumption are proportional to one another, the proportionality factor being the consumer’s discount rate. These results indicate that the main restrictions of the univariate model are preserved in the multivariate model.
The conditions in which the model is shown to be dynamically stable are derived. When the model is stable, the solution will have exactly 2n real roots, n of the roots falling within the unit circle and n falling outside the unit circle. The smaller roots can be used to solve the problem backward in time, or to express the current-period solution conditional on the levels of consumption of all goods in the previous period. The set of larger roots are used to express current consumption as a linear function of all future prices. Short-run and Long-run elasticity formulas for the multivariate version are derived and are shown to be generalizations of the univariate version.
Estimation can be undertaken on one of three different forms: 1) The first-order conditions directly, Equation (15); 2) the so-called structural form, Equation (16); or 3) the reduced form, Equation (18). Which of the above approaches to estimation is best can only be determined through further empirical work. Regardless of the approach taken for estimation, the theoretical framework developed in this paper should prove useful to researchers modeling addictive goods that are interrelated in consumption.
8. Acknowledgements
Research supported in part by the North Carolina Agricultural Research Service, Raleigh, North Carolina, 27695.
REFERENCES
- G. Becker., M. Grossman and K. Murphy, “An Empirical Analysis of Cigarette Addiction,” American Economic Review, Vol. 84, No. 3, 1994, pp. 396-418.
- M. Bask and M. Melkersson, “Rationally Addicted to Drinking and Smoking,” Applied Economics, Vol. 36, No. 4, 2004, pp. 373-381. doi:10.1080/00036840410001674295
- P. Pierani and S. Tiezzi, “Addiction and Interaction between Alcohol and Tobacco Consumption,” Empirical Economics, Vol. 37, No. 1, 2009, pp. 1-23. doi:10.1007/s00181-008-0220-3
- L. Phlips, “Applied Consumption Analysis,” North-Holland Publishing Co., Amsterdam, 1983.
- R. Lucas, “Optimal Investment Policy and Flexible Accelerator,” International Economic Review, Vol. 8, No. 1, 1967, pp. 78-85. doi:10.2307/2525383
- T. Sargent, “Macroeconomic Theory,” Academic Press, New York, 1979.
- W. Diewert and T. Wales, “Flexible Functional Forms and Global Curvature Conditions,” Econometrica, Vol. 55, No. 1, 1987, pp. 43-68. doi:10.2307/1911156
NOTES
1Becker, Grossman, and Murphy [1] also include unobserved lifecycle variables in the utility function. These variables could easily be accommodated in the multivariate version but are not included to simplify the model. For econometric implementations, the main implication is that we would need to assume both lagged and future quantities are endogenous variables because inclusion of lifecycle variables would imply the error term would have a moving average structure.
2Because the price of the composite good is 1, each price of the consumption goods is deflated by the price of the composite good.
3The assumption that λ is constant over the planning horizon is precisely what the model implies. With perfect certainty, the consumer would expect to choose life-time consumption allocations holding λ constant.
4In this specification, the effect of a change in lagged consumption of the jth variable on current consumption of the ith good (holding future consumption constant) is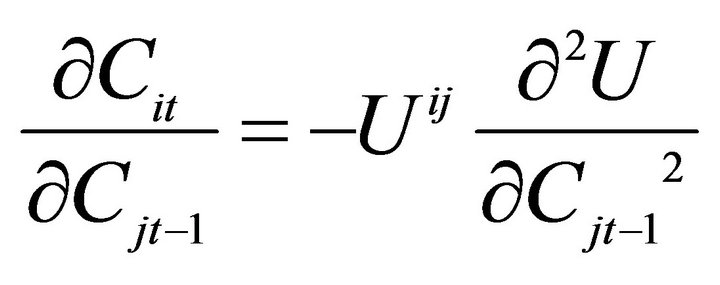 , where
, where  is the i,jth element of the inverse of the matrix
is the i,jth element of the inverse of the matrix . Thus, current and lagged consumption arestill interdependent when expressed in this form.
. Thus, current and lagged consumption arestill interdependent when expressed in this form.
5This specification generalizes [2] and [3], who also make the marginal utility of  independent of
independent of .
.
6The quadratic function is not necessary but is introduced in order to evaluate the stability of the system in the neighborhood of the stationary equilibrium. See [1] for a similar approach in the univariate case.
7The lag operator 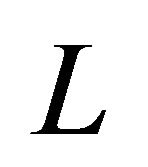 is defined as follows:
is defined as follows: 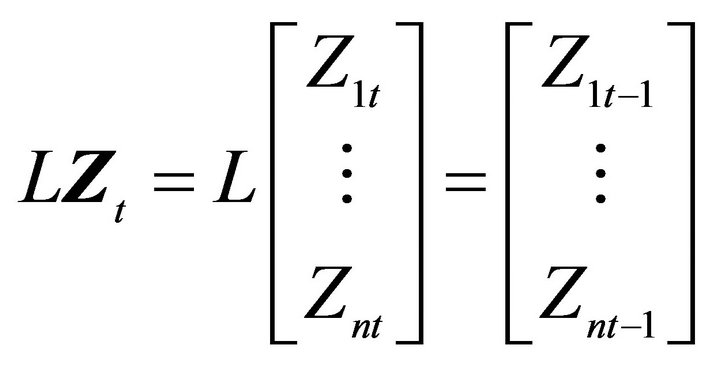 and
and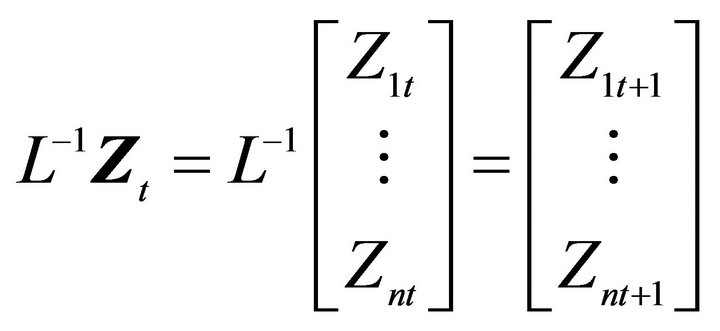 for any arbitrary vector
for any arbitrary vector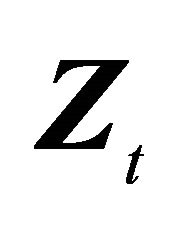 .
.
8The matrix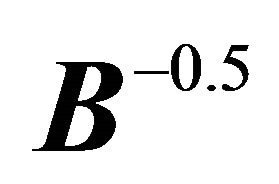 is the diagonal matrix whose elements are the reciprocals of the square roots of the
is the diagonal matrix whose elements are the reciprocals of the square roots of the  ‘s. This means then that the matrix
‘s. This means then that the matrix 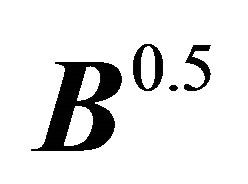 is the diagonal matrix whose elements are the square roots of the
is the diagonal matrix whose elements are the square roots of the 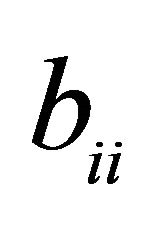 ‘s.
‘s.
9To see this, note that . If
. If  then
then 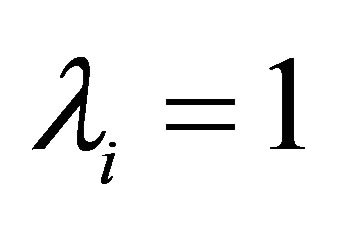 using (12). So because
using (12). So because 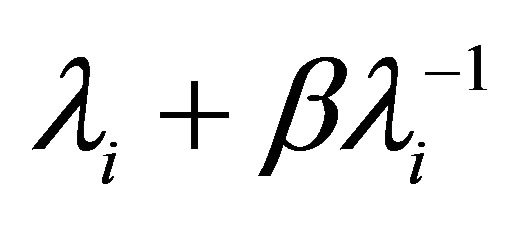 is decreasing in
is decreasing in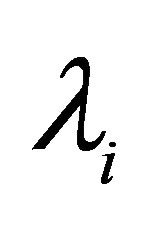 ,
,  in order for
in order for 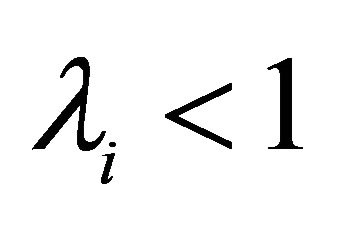 [6].
[6].
10We follow [1] in approximating the product of the marginal utility of income and price by a linear function in income and the price. The fixed marginal utility of wealth multiplying price in the linear approximation is then normalized to unity by dividing both sides of the equation by the fixed constant. Since this constant is the same for all equations, the general forms of the matrices in Equation (15) are unchanged.
11Of course, we assume that distribution of effects across individual consumers is relatively constant over time so that 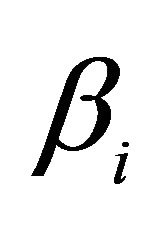 can be taken as constant. Otherwise, we would need to modify the model to make
can be taken as constant. Otherwise, we would need to modify the model to make  a function of variables characterizing changes in the distribution, e.g., proportion of population in different age groups.
a function of variables characterizing changes in the distribution, e.g., proportion of population in different age groups.

