Theoretical Economics Letters
Vol. 2 No. 1 (2012) , Article ID: 17359 , 8 pages DOI:10.4236/tel.2012.21010
Contestability and Collateral in Credit Markets with Adverse Selection
Department for Prime Minister and Cabinet, Rome, Italy
Email: g.cesaroni@governo.it
Received November 4, 2011; revised December 16, 2011; accepted December 22, 2011
Keywords: Adverse Selection; Collateral; Rationing; Contestable Markets
ABSTRACT
The work discusses a basic proposition in the theory of competition in markets with adverse selection. By working out the sequence of market transactions, we show that the effectiveness of collateral in avoiding equilibrium rationing depends on an assumption of uncontestability of the loan market. If contestability is restored to its proper place, the separation of borrower by means of sufficient collateral does not impede the emergence of credit rationing, which results from a coordination failure among risk-neutral banks. As a consequence, even in a risk-neutral environment with suitable endowments, the use of collateral in credit contracts could not be a socially efficient screening-device. Our conclusion on rationing does not stand in contrast with a general result from Gale.
1. Introduction
Since the seminal work of Bester [1], it has been generally taken for granted that in a risk-neutral environment, when sufficient wealth is made available from a borrower’s endowment, the competitive equilibrium of the credit market achieves perfect sorting, thus solving the adverse selection problem posed by Stiglitz and Weiss [2]. In other words, the separation of borrowers, which is accomplished by means of “unlimited” collateral, impedes equilibrium rationing. This conclusion has become a real cornerstone in the literature on credit markets with asymmetric information, as it has been shared by several diverse contributions (e.g., Bester [3], Besanko and Thakor [4], Hellwig [5], Stiglitz and Weiss [6], SchmidtMohr [7]), and it has also been recalled by authors dealing with the more general problem of competition in markets with adverse selection (Gale [8]).
Our paper discusses this proposition by rendering explicit the whole sequence of market transactions, and considering the symmetric incentive-compatible equilibrium of the resulting market game. We point out that Bester’s claim relies on an ad hoc assumption, which removes contestability of the loan market in presence of a rationing equilibrium. In fact, an artificial restriction of the strategies of the incumbent banks is being imposed, while this restriction does not equally hold for the nonrationing equilibrium. Conversely, if the game is correctly specified, in the sense that the same extensive form and the same unrestricted strategy set is being considered for both kinds of possible equilibria (rationing and nonrationing), then Bester’s conclusion is not valid. The result extends easily to the case in which a recourse opening of the credit market is being added. Then, a competitive equilibrium with separation of borrowers can in fact show rationing of their demand for credit, even when they have sufficient collateral. As a direct consequence, one has that collateralization may turn out to be a sociallyinefficient instrument in screening a borrower’s riskiness.
The paper is organized as follows: in Section 2, we illustrate the basic model; in Section 3, we introduce the definition of equilibrium and the extensive form of the game; Section 4 deals with the central issue of the presence of rationing in an equilibrium and Section 5 concludes with a discussion of the results of our analysis and their relationship with the above mentioned strands of literature.
2. The Model
Given his purpose, Bester1 obviously employs a model that reproduces the same basic structure of Stiglitz and Weiss [2] analysis. All agents are risk-neutral and there are two types of entrepreneurs or firms. Each entrepreneur has a fixed-scale investment opportunity, while the random returns of investments of the two classes of firms are ordered according to the mean preserving spread (MPS) criterion2. Banks cannot directly observe the type of borrower they deal with, so adverse selection may arise. The supply of deposits to the banking system is a continuous and strictly increasing function of the rate of interest paid on deposits. In a credit contract, banks may charge collateral as a guarantee for loan repayments when the borrower defaults. Pledging collateral is costly to borrowers, who face a generic and constant unit cost. Moreover, they have a collateral endowment which is more than sufficient to fully guarantee the loan value. Symbols are as follows: I is the fixed scale of investment,  is their random return, taking values in
is their random return, taking values in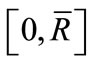 , where
, where 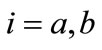 stands for the type of firm we are considering;
stands for the type of firm we are considering; ,
, 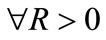 , is the distribution function: assuming that type b entrepreneurs are more risky than type a, in the sense of a mean-preserving spread, we have
, is the distribution function: assuming that type b entrepreneurs are more risky than type a, in the sense of a mean-preserving spread, we have

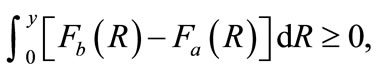 ;
;
W is the initial endowment of monetary wealth each entrepreneur can dispose of (W < I), B = I – W is the amount of funds needed to start any investment project;  is the supply function of deposits; finally C and r denote, respectively, the collateral and the nominal rate of interest charged on a loan, k is the unit cost of collateral and π is the rate of interest banks pay on deposits. There are Ni entrepreneurs of type i. Note that the nonmonetary wealth entrepreneurs can offer as collateral is separated from their monetary holdings. The debt contract the banks use to lend funds to firms declares the borrower to be insolvent anytime the sum of total return on investments and collateral is not sufficient for loan repayment: that is when
is the supply function of deposits; finally C and r denote, respectively, the collateral and the nominal rate of interest charged on a loan, k is the unit cost of collateral and π is the rate of interest banks pay on deposits. There are Ni entrepreneurs of type i. Note that the nonmonetary wealth entrepreneurs can offer as collateral is separated from their monetary holdings. The debt contract the banks use to lend funds to firms declares the borrower to be insolvent anytime the sum of total return on investments and collateral is not sufficient for loan repayment: that is when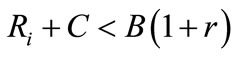 . In this circumstance the bank seizes the whole disposable value
. In this circumstance the bank seizes the whole disposable value 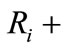
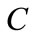 , otherwise it receives the contractual repayment
, otherwise it receives the contractual repayment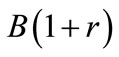 . Bester considers only contracts for which the collateral does not exceed the face value of the loan
. Bester considers only contracts for which the collateral does not exceed the face value of the loan  (otherwise default would be trivially excluded from the model). The bank’s expected rate of return on a loan contract
(otherwise default would be trivially excluded from the model). The bank’s expected rate of return on a loan contract 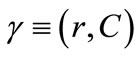 to borrower i is
to borrower i is
 (1)
(1)
From the same contract, entrepreneur i expects to gain a total profit which is given as
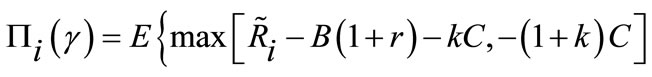 (2)
(2)
For , the MPS ordering implies that
, the MPS ordering implies that
 (3)
(3)
and
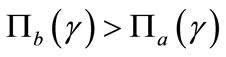 (4)
(4)
For a given contract γ, a bank obtains a higher rate of return on a loan to a less-risky borrower, while the utility of a riskier borrower is higher than that of a safer one. Totally differentiating expressions (1) and (2) with respect to r and C, and simplifying, we get the following marginal rates of substitution
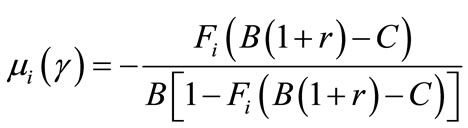 (5)
(5)
and
 (6)
(6)
These ratios clearly indicate that each kind of borrower has an indifference curve which is steeper in absolute value than its isoprofit curve, because 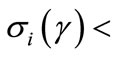
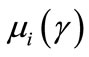 . Moreover, it can easily be shown that both the isoreturn curves are strictly convex, so that functions
. Moreover, it can easily be shown that both the isoreturn curves are strictly convex, so that functions 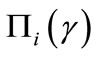 are quasi-convex. The property is not grasped by Bester, who believes these curves not to be concave everywhere3. However, in this model, a sufficient condition to obtain a separating equilibrium is represented by
are quasi-convex. The property is not grasped by Bester, who believes these curves not to be concave everywhere3. However, in this model, a sufficient condition to obtain a separating equilibrium is represented by 
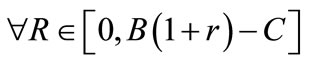 , an assumption which amounts to establishing a single-crossing property for the isoreturn curves. In fact, for any given contract, we immediately get that the indifference curve of riskier investors, those of type b, becomes steeper than that of less risky investors,
, an assumption which amounts to establishing a single-crossing property for the isoreturn curves. In fact, for any given contract, we immediately get that the indifference curve of riskier investors, those of type b, becomes steeper than that of less risky investors,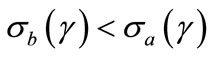 . The same goes for the isoprofit curves. Thus, the separate indifference (or isoprofit) curves will have one intersection point at most. As far as their shape is concerned, it will be more convenient to adopt Bester’s representation here. Finally, two important features of his model have to be emphasized:
. The same goes for the isoprofit curves. Thus, the separate indifference (or isoprofit) curves will have one intersection point at most. As far as their shape is concerned, it will be more convenient to adopt Bester’s representation here. Finally, two important features of his model have to be emphasized:
Assumption 1: banks act as perfect competitors, that is, each bank takes the rate of interest π on deposits and the set of credit offers by competing banks as given and as independent of its own actions;
Assumption 2: an entrepreneur who is rationed at his preferred contract may successively apply for the other contract at the same bank4.
As we shall see later on, assumption 2 is crucial for obtaining Bester’s conclusion on the absence of rationing.
3. Definition of Equilibrium and the Extensive Form of the Market Game
We will now have a preliminary insight into the basic definition of equilibrium and into the sequence of transactions, that are featured by the model we have just presented.
Definition 1
A credit market equilibrium is a situation in which borrowers choose among contracts to maximize expected profits: 1) each contract 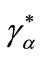 and
and  yields zero profit to the bank; 2) any additional credit offer γ will make no profits; and 3) there is no excess supply of funds5.
yields zero profit to the bank; 2) any additional credit offer γ will make no profits; and 3) there is no excess supply of funds5.
This equilibrium is shortly denoted as a tuple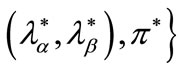
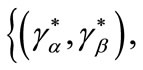 , where
, where ,
, 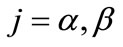
 , is the fraction of firms that receive credit under the terms of
, is the fraction of firms that receive credit under the terms of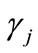 , that is to say each firm’s identical probability of getting credit6; moreover, by requirement 1),
, that is to say each firm’s identical probability of getting credit6; moreover, by requirement 1),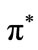
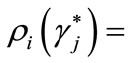 . Credit rationing occurs if some entrepreneur i faces a positive probability of being rejected at contract
. Credit rationing occurs if some entrepreneur i faces a positive probability of being rejected at contract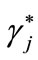 , which he prefers, and at the same time
, which he prefers, and at the same time 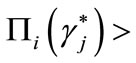
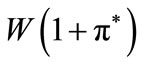 . Notice that the sign of strict inequality comes from the need to satisfy the credit-market participation constraint of entrepreneurs:
. Notice that the sign of strict inequality comes from the need to satisfy the credit-market participation constraint of entrepreneurs:
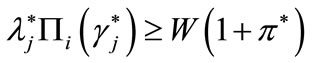 (7)
(7)
where the second term is the alternative return the entrepreneur can obtain from his monetary wealth; this condition is also known as the individual rationality constraint (IR).
In an equilibrium with separation of different borrowers, their incentive-compatibility constraints (IC) must also hold:
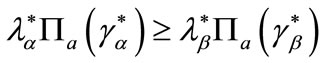 (8)
(8)
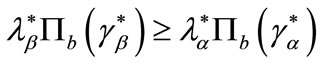 (9)
(9)
The equilibrium is depicted in Figure 1 below, where a and b represent the borrowers’ indifference curves while α and β denote a bank’s isoprofit curve of the corresponding type. As long as the proportion between high-risk and low-risk borrowers is so high as to exclude the existence of a dominating pooling contract7, the competitive equilibrium—a Nash equilibrium—exists, and is given by the separating pair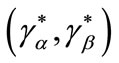 . Bester’s contention is that in this framework there can be no rationing of any type of borrowers at
. Bester’s contention is that in this framework there can be no rationing of any type of borrowers at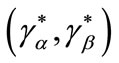 , that is to say
, that is to say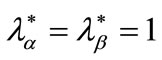 .
.
To address this issue, it will be useful to describe more precisely the sequence of market transactions which is posited by Bester. With regard to the sequence of transactions, the timing of the model can be illustrated as follows (Figure 2).
In the time-line below, we have uninformed agents (banks) moving first: they devise debt contracts to be offered to the informed ones (borrowers) (see Hellwig [5]). But price terms of this contract, i.e.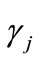 , depend on the rate of interest on deposits, so an equilibrium on this market must be computed before banks can actually offer loans. If so, banks who have decided to enter the loans market must go first on the deposits market, where they demand a quantity of loanable funds corresponding to the credit probabilities they are going to offer and to the expected number of borrowers. The matching of these demands with the supply of funds from savers,
, depend on the rate of interest on deposits, so an equilibrium on this market must be computed before banks can actually offer loans. If so, banks who have decided to enter the loans market must go first on the deposits market, where they demand a quantity of loanable funds corresponding to the credit probabilities they are going to offer and to the expected number of borrowers. The matching of these demands with the supply of funds from savers, 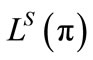 , determines a notional equilibrium rate of interest on deposits,
, determines a notional equilibrium rate of interest on deposits,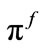 . This, in principle, need not be the actual equilibrium rate as long as trading is not definitively closed (compare however assumption 3 below). On the other hand, when offers are made by banks, a generic borrower can observe this rate and accordingly chooses one of the two alternative options: investing his liquidity on the deposits market or applying for his preferred credit-offer at a single bank. Once credit applications by
. This, in principle, need not be the actual equilibrium rate as long as trading is not definitively closed (compare however assumption 3 below). On the other hand, when offers are made by banks, a generic borrower can observe this rate and accordingly chooses one of the two alternative options: investing his liquidity on the deposits market or applying for his preferred credit-offer at a single bank. Once credit applications by

Figure 1. Bester’s equilibrium.
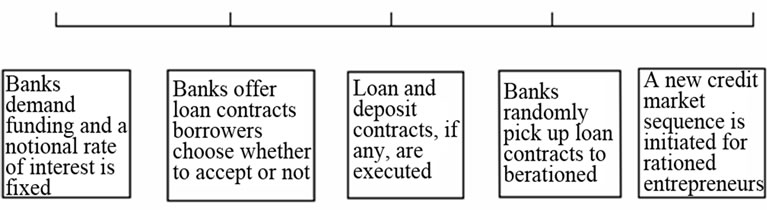
Figure 2. The timing of transactions.
borrowers have been made, banks randomly choose the individual loans which are going to be financed.
We are now in the position to describe in some detail the functioning of markets along with the extensive form of the game which a representative bank plays with a generic borrower of a specified kind. In Bester’s model a symmetric separating-equilibrium is considered, in which different banks and different entrepreneurs of a given risk-class behave the same way. The rate of interest on the market for deposits in a symmetric equilibrium in which banks offer credit with a positive probability, and in which firms demand loans, can be determined as
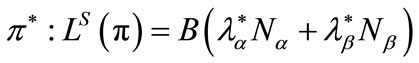 (10)
(10)
where, obviously, the right-hand term of the equation is the banks’ total demand of funds.
There is a large number of banks, E, and the market for loans is contestable. A number of banks H < E that is sufficient to serve the whole market for loans, will enter the credit market, therefore a borrower can be assured that  is the actual probability of receiving a loan. The extensive form of the simple game played by a representtative bank, which plans to enter the credit market, and by a generic borrower of type i may be depicted as in Figure 3 below.
is the actual probability of receiving a loan. The extensive form of the simple game played by a representtative bank, which plans to enter the credit market, and by a generic borrower of type i may be depicted as in Figure 3 below.
Herein, 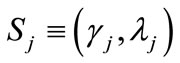 is the loan offer - which probability determines the equilibrium rate of interest on deposits
is the loan offer - which probability determines the equilibrium rate of interest on deposits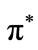 ,
,  and
and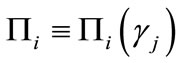 ; while X is the absolute value of the loss that a bank incurs should entrepreneurs refuse its contract offer: i.e. the value of the deposit contracts. Strategy E denotes exit from the credit market, A is the acceptance of the loan offer; L and NL, respectively, stand for according a loan or not, and such strategies are randomly chosen by the bank. As far as trading on the market for deposits is concerned, it must be observed that the following assumption is im-
; while X is the absolute value of the loss that a bank incurs should entrepreneurs refuse its contract offer: i.e. the value of the deposit contracts. Strategy E denotes exit from the credit market, A is the acceptance of the loan offer; L and NL, respectively, stand for according a loan or not, and such strategies are randomly chosen by the bank. As far as trading on the market for deposits is concerned, it must be observed that the following assumption is im-
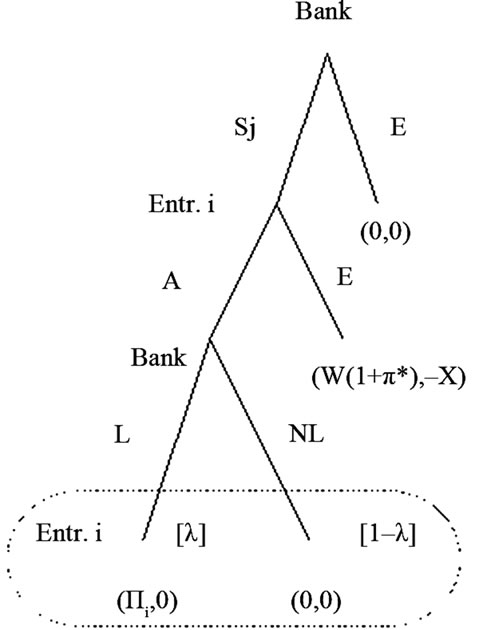
Figure 3. The market-game tree.
plicit in Bester’s model:
Assumption 3: Trading on this market is completed before borrowers accept credit offers, so the deposits market precedes the loans market, i.e. definitive fixing of the rate of interest and execution of the deposit contracts —by banks and savers—take place before the market for loans closes.
Comment. On the contrary, suppose that banks can sign deposit contracts after having observed the entrepreneurs’ decision to accept or refuse the loan offer. Then, when borrowers found it favorable to refuse their preferred credit offer, because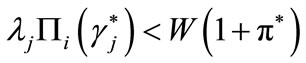 , banks would no longer demand funding on the deposits market and
, banks would no longer demand funding on the deposits market and 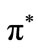 would go to zero. If this occurs, payoffs from the equilibrium sequence
would go to zero. If this occurs, payoffs from the equilibrium sequence 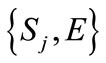 would simply be
would simply be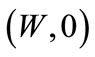 , on this basis it cannot be excluded that
, on this basis it cannot be excluded that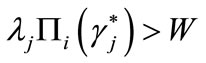 . From this we have an obvious comment on the trading structure: if closure of trade on the deposits and on loans market was simultaneous then, in equilibrium, entrepreneurs could demand a loan even if their participation constraint (IR) to the credit market was violated. This proves the necessity of assumption 3.
. From this we have an obvious comment on the trading structure: if closure of trade on the deposits and on loans market was simultaneous then, in equilibrium, entrepreneurs could demand a loan even if their participation constraint (IR) to the credit market was violated. This proves the necessity of assumption 3.
Now that the basic framework of Bester’s model has been described, let us consider a simple implication of his pivotal Assumption 2.
Lemma 1
Assumption 2 implies a second stage of the credit market, in which banks offer the new set of contracts to rationed borrowers and demand additional funding on the deposits market.
Proof. Suppose not. Then assumption 2 would entail a market in which banks demand funding just once and offer borrowers a lottery over loan contracts , where each lottery yields zero profit to a bank. The lottery is such that a type a firm will be offered contract
, where each lottery yields zero profit to a bank. The lottery is such that a type a firm will be offered contract  and a credit-probability
and a credit-probability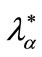 , while in the event that it should be rationed at this contract (an outcome which has probability
, while in the event that it should be rationed at this contract (an outcome which has probability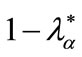 ) this firm will be offered contract
) this firm will be offered contract  and a credit-probability
and a credit-probability . Mutatis mutandum, the same goes for a type b firm. In this market environment, Bester’s IR and IC constraints (7)-(9) and the zero-profit condition
. Mutatis mutandum, the same goes for a type b firm. In this market environment, Bester’s IR and IC constraints (7)-(9) and the zero-profit condition  do not hold anymore, while the proof of his Theorem 1 is inapplicable.
do not hold anymore, while the proof of his Theorem 1 is inapplicable.
Before we go further, another minor—but useful— observation can be advanced in relation to the differential information among banks, which can arise at stage two of the credit market: with a separating equilibrium, at the end of the first credit market an incumbent bank knows the risk features of its customers/borrowers, while a bank which is a potential entrant does not. This shows the feasibility of the pivotal assumption 2. Obviously, it is due to the fact that—in the first credit market—the equilibrium pair of contracts 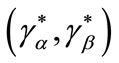 is incentive compatible and self-selection of borrowers is induced. So, Lemma 1 tells us that, in the event of rationing, assumption 2 yields a second stage of the credit market, a stage in which incumbent banks offer a specific contract— namely the one that was designed for the other type—to borrowers they have just rationed. Thus, with regard to the extensive form of the game, the presence of rationing in equilibrium adds a second game tree to the initial one; this new tree has the same general structure of the first (see Figure 3 above) and differs only in the agents’ payoffs. Accordingly, we can point out
is incentive compatible and self-selection of borrowers is induced. So, Lemma 1 tells us that, in the event of rationing, assumption 2 yields a second stage of the credit market, a stage in which incumbent banks offer a specific contract— namely the one that was designed for the other type—to borrowers they have just rationed. Thus, with regard to the extensive form of the game, the presence of rationing in equilibrium adds a second game tree to the initial one; this new tree has the same general structure of the first (see Figure 3 above) and differs only in the agents’ payoffs. Accordingly, we can point out
Remark 1
The extensive form of the whole game is not independent from the type of equilibrium that has to be determined.
4. Equilibrium with Rationing or Not?
We will now discuss the central issue: what credit probabilities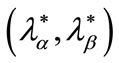 must be assigned to the incentive-compatible equilibrium pair of contracts
must be assigned to the incentive-compatible equilibrium pair of contracts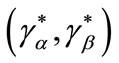 ? Bester’s theorem 1 argues that these probabilities equal one.
? Bester’s theorem 1 argues that these probabilities equal one.
Proposition 1 (Bester’s result)
Let 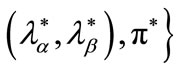
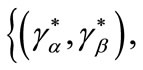 be a credit market equilibrium at stage one, and let both contracts
be a credit market equilibrium at stage one, and let both contracts  and
and  be demanded by entrepreneurs. Moreover these contracts are incentive compatible. Then in a credit market equilibrium there is no rationing at
be demanded by entrepreneurs. Moreover these contracts are incentive compatible. Then in a credit market equilibrium there is no rationing at  or at
or at , i.e.
, i.e.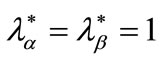 .
.
Proof. See Bester [1], pp. 853-854 Bester’s proof is by contradiction. He denies that credit probabilities equal one in the incentive-compatible equilibrium, and then shows that, in presence of rationing of some fraction of firms, there exists a deviating credit offer which warrants a positive profit to a generic entrant bank. This is a contradiction to requirement 1) of the definition of an equilibrium8, thus the proposition is proven.
Comment. In any case, the deviating offer could be allowed only by way of assumption 2. In fact, this assumption puts, in the second stage of the credit market, a completely arbitrary restriction on the strategy set of the incumbent banks. In the first credit market, these banks can freely determine their credit offers, while in the second market assumption 2 forces their strategy set—for a rationed borrower of a given type—to be made up of the remaining contract offered at stage one: 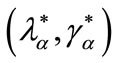 for a type b firm,
for a type b firm, 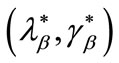 for a type a firm. On the contrary, entrant banks—Bester’s “competing banks”—have access to an unrestricted set of strategies. In this setting, incumbent banks do not actually offer the above contracts to rationed borrowers9, and for this reason the reservation utility of these borrowers falls from
for a type a firm. On the contrary, entrant banks—Bester’s “competing banks”—have access to an unrestricted set of strategies. In this setting, incumbent banks do not actually offer the above contracts to rationed borrowers9, and for this reason the reservation utility of these borrowers falls from  to
to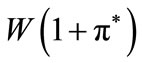 . Thus, trivially, a deviating profitable offer by an entrant bank is allowed to exist. These observations clearly indicate that we may be in presence of a formal fallacy—due to assumption 2—which should invalidate Bester’s result. To check this, the logical problem has to be properly set up, that is:
. Thus, trivially, a deviating profitable offer by an entrant bank is allowed to exist. These observations clearly indicate that we may be in presence of a formal fallacy—due to assumption 2—which should invalidate Bester’s result. To check this, the logical problem has to be properly set up, that is:
a) The strategy set of incumbent banks must not be restricted when there is rationing—as it is actually contemplated for the non-rationing equilibrium;
b) The extensive form of the game tree must be given independently from the type of equilibrium which we are solving for.
These two logical requirements imply the removal of assumption 2. Therefore, we can limit ourselves to ascertaining what happens in a credit market equilibrium whose game tree is entirely described by Figure 3 above, that is, stage one of the credit market. Herein, we derive our main result
Proposition 2
Let 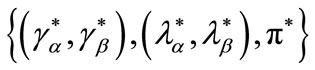 be a credit market equilibrium at stage one, and let both contracts
be a credit market equilibrium at stage one, and let both contracts 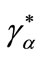 and
and 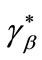 be demanded by entrepreneurs. Moreover these contracts are incentive compatible and assumption 2 does not hold. Then in a credit market equilibrium there can be rationing at
be demanded by entrepreneurs. Moreover these contracts are incentive compatible and assumption 2 does not hold. Then in a credit market equilibrium there can be rationing at 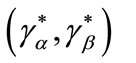 i.e.
i.e.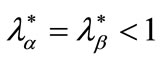 .
.
Proof. See appendix.
Comment. Essentially, we prove the impossibility of constructing a profitable deviating offer in the presence of rationing. It can be even remarked that an identical result is obtained if we are ready to abandon requirement b), thus allowing for a second stage of the credit market10. Nevertheless, note that this recourse opening would have no economic or behavioral justification in this static credit model: banks have already screened and rationed their borrowers, and have no motivation for offering rationed borrowers a new contract. We conclude that Bester’s result on the absence of rationing is a circular reasoning based on the arbitrary restriction of the strategy set which is imposed, in the occurrence of rationing, only upon the incumbent banks.
5. Discussion
In this model, we have argued that an equilibrium with separation of borrowers is compatible with rationing. If banks fix a credit probability of less than one, then equilibrium rationing11 arises as a coordination failure among risk-neutral agents. When the market for loans is contestable12 there is no way for banks to design a profitable deviant contract-pair that satisfies individual rationality of entrepreneurs and enhances their probability of credit. The occurrence of rationing in a separating equilibrium questions the efficiency of collateral as a screening instrument of borrowers’ riskiness. Hitherto, when compared to a pooling equilibrium, the costs associated with the introduction of collateral have been justified by the social gains ensuing from the elimination of rationing in a separating equilibrium, viz. a strict increase in the number of social efficient investment projects undertaken, i.e. projects for which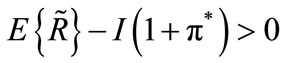 . Conversely, as we have argued, credit rationing can resist the introduction of collateral, in this case the number of these projects is not necessarily higher than that of a pooling equilibrium, while less-risky borrowers have to pay the cost of it out of their collateralizable wealth. In the separating equilibrium we examined, social surplus V is given as:
. Conversely, as we have argued, credit rationing can resist the introduction of collateral, in this case the number of these projects is not necessarily higher than that of a pooling equilibrium, while less-risky borrowers have to pay the cost of it out of their collateralizable wealth. In the separating equilibrium we examined, social surplus V is given as:


where 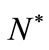 is the number of entrepreneurs who receive a loan, while the second addend represents the cost of pledging collateral, borne by type a entrepreneurs. Clearly, if the increase in the number of financed projects is not sufficient to compensate for collateral costs, social surplus will diminish and the use of collateral in credit contracts will not result in a socially-efficient outcome13.
is the number of entrepreneurs who receive a loan, while the second addend represents the cost of pledging collateral, borne by type a entrepreneurs. Clearly, if the increase in the number of financed projects is not sufficient to compensate for collateral costs, social surplus will diminish and the use of collateral in credit contracts will not result in a socially-efficient outcome13.
Finally, we can discuss the relationship of our analysis to the literature. To our knowledge, the flaws of Bester [1] analysis have never been detected. For this reason, perhaps, it has been generally taken for granted that introduceing collateral in an analytical framework à la Stiglitz and Weiss [2] would have definitely excluded rationing from its credit market equilibrium14. We note that our conclusion offers a substantial, and totally unexpected, extension of the validity of the first Stiglitz and Weiss explanation for rationing, which relied on pooling and on a different concept of equilibrium. Basically, it should be emphasized that rationing in a separating allocation, with risk-neutral entrepreneurs and a solution that is not bound by borrower’s endowment of collateral, can now be achieved. Contrary to Stiglitz and Weiss [6], to explain equilibrium credit-rationing, we show that there is no need to assume the joint presence of adverse selection, moral hazard and entrepreneurs’ risk-aversion. But, most of all, the characteristic that confers generality to our result is the slackness of the collateral constraint. In fact, when indivisible projects are available, a binding constraint has constituted the key assumption for reaching a credit-rationing equilibrium in presence of both collateral and separation of borrowers. This binding condition has been equally shared by models with diverse specifications (see Besanko and Thakor [4], Bester [3], Stiglitz and Weiss [6]15). Not surprisingly, as we have examined Bester’s model, our competitive-equilibrium concept differs from that of Stiglitz and Weiss [2], where banks maximized the depositors’ rate of return as they were monopolistic competitors on the market for loanable funds. Nevertheless, it is identical to the Stiglitz and Weiss [6] concept. As for this point, observe that: a) the Stiglitz and Weiss [2] definition of equilibrium is a more conducive assumption for equilibrium rationing (see Chan and Thakor [15]); b) considering banks that are monopolistic competitors for deposits would easily bring about equilibrium-rationing in Bester’s framework16. Therefore, the use of a different concept of equilibrium adds to the significance of our main conclusion.
Remarkably, our proposition about the coexistence of screening and equilibrium rationing does not stand in contrast with the results of Gale [8]. This general contribution follows a Walrasian approach, in a risk-neutral context where each contract makes up a single market and agents take the probability of being able to exchange any particular contract as given. Price terms are exogenous, i.e. defined only implicitly by contracts which are indeed identified with probability distributions over a set of outcomes, so that markets are to be balanced by adjusting the probability of trade. Herein, Gale proves that equilibrium rationing will not be observed unless agents are indifferent to trade (i.e. borrowers get their reservation utility), the result depending on an assumption which is a generalization of the familiar single-crossing property. Nevertheless, we point out that rationing in our case does not contradict Gale’s theorem, in that it can be easily ascertained that a single-crossing property holds but the first part of Gale’s assumption is clearly violated17. In fact, in a Rothschild and Stiglitz [16] type of analysis, like the one undertaken, we have no finiteness of the space of contracts. This could indeed be a reason for that violation and for the fact that, if put in this different context, Gale’s assumption may reveal itself to be much stronger than the familiar single-crossing property18.
REFERENCES
- H. Bester, “Screening vs. Rationing in Credit Markets with Imperfect Information,” American Economic Review, Vol. 75, No. 4, 1985, pp. 850-855
- J. E. Stiglitz and A. Weiss, “Credit Rationing in Markets with Asymmetric Information,” American Economic Review, Vol. 71, No. 3, 1981, pp. 393-410.
- H. Bester, “The Role of Collateral in Credit Markets with Imperfect Information,” European Economic Review, Vol. 31, No. 4, 1987, pp. 887-889. doi:10.1016/0014-2921(87)90005-5
- D. Besanko and A. V. Thakor, “Collateral and Rationing: Sorting Equilibria in Monopolistic and Competitive Credit Markets,” International Economic Review, Vol. 28, No. 3, 1987, pp. 671-689. doi:10.2307/2526573
- M. Hellwig, “Some Recent Developments in the Theory of Competition in Credit Markets with Adverse Selection,” European Economic Review, Vol. 31, No. 1-2, 1987, pp. 319-325. doi:10.1016/0014-2921(87)90046-8
- J. E. Stiglitz and A. Weiss, “Asymmetric Information in Credit Markets and its Implications for Macroeconomics,” Oxford Economic Papers, Vol. 44, No. 4, 1992, pp. 694-724.
- U. Schmidt-Mohr, “Rationing versus Collateralization in Competitive and Monopolistic Credit Markets with Asymmetric Information,” European Economic Review, Vol. 41, No. 7, 1997, pp.1321-1342. doi:10.1016/S0014-2921(96)00006-2
- D. Gale, “Equilibria and Pareto Optima of Markets with Adverse Selection,” Economic Theory, Vol. 7, No. 2, 1996, pp. 207-235.
- M. Rothschild and J. E. Stiglitz, “Increasing Risk: I. A Definition,” Journal of Economic Theory, Vol. 2, No. 3, 1970, pp. 225-243. doi:10.1016/0022-0531(70)90038-4
- C. A. E. Goodhart, “Money, Information and Uncertainty,” Macmillan, London, 1989.
- X. Freixas and J. C. Rochet, “Microeconomics of Banking,” MIT Press, Cambridge, 1998.
- W. Keeton, “Equilibrium Credit Rationing,” Garland Press, New York, 1979.
- D. M. Jaffee and J. E. Stiglitz J. E, “Credit Rationing,” In: B. M. Friedman and F. Hahn, Eds., Handbook of Monetary Economics, North Holland, Amsterdam, 1990.
- W. Baumol, J. Panzar and R. Willig, “Contestable Markets and the Theory of Industry Structure,” Harcourt Brace Jovanovic, New York, 1982.
- Y. S. Chan and A. V. Thakor, “Collateral and Competitive Equilibria with Moral Hazard and Private Information,” Journal of Finance, Vol. 42, No. 2, 1987, pp. 345- 363. doi:10.2307/2328256
- M. Rothschild and J. E. Stiglitz, “Equilibrium in Competitive Insurance Markets: An Essay on the Economics of Imperfect Information,” Quarterly Journal of Economics, Vol. 90, No. 4, 1976, pp. 629-649. doi:10.2307/1885326
Appendix
Proof of Proposition 2 The only route to prove the possibility of a profitable deviating offer is that of ascertaining—for any arbitrary credit probability 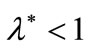 the existence of price terms
the existence of price terms 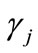
such that 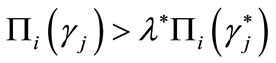 and
and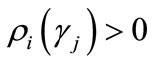 ,
, 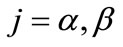
and ; hence,
; hence, . That is to say, the deviating offer we are searching for has credit probability
. That is to say, the deviating offer we are searching for has credit probability  and price terms
and price terms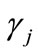 , which are—for borrowers— slightly worse than
, which are—for borrowers— slightly worse than 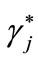 in order to allow for a positive bank-profit. Following Bester, we can think of
in order to allow for a positive bank-profit. Following Bester, we can think of 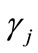 as being different from
as being different from 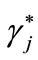 only because of a small increase in the rate of interest
only because of a small increase in the rate of interest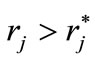 , while collateral stays unchanged, i.e.
, while collateral stays unchanged, i.e. 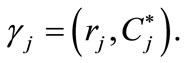 In principle, this problem may appear easy to solve. In fact, expected-utility
In principle, this problem may appear easy to solve. In fact, expected-utility  is a continuous function which is monotone with respect to r, because its partial derivative
is a continuous function which is monotone with respect to r, because its partial derivative 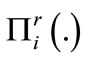 is always negative. Then function
is always negative. Then function 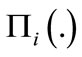 can be inverted and a threshold value
can be inverted and a threshold value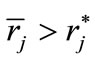 , such that
, such that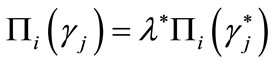 , can be determined. Afterwards, we can choose
, can be determined. Afterwards, we can choose 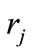 as the highest value that satisfies
as the highest value that satisfies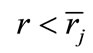 , so that
, so that 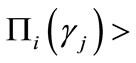
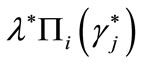 with
with 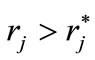 would generally follow. Note, however, that
would generally follow. Note, however, that 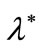 can be arbitrarily near to 1 and, as a consequence,
can be arbitrarily near to 1 and, as a consequence, 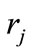 and
and 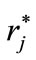 can be practically indistinguishable
can be practically indistinguishable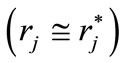 . In practice, it is difficult to affirm that the sought-after deviating offer will exist for any
. In practice, it is difficult to affirm that the sought-after deviating offer will exist for any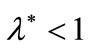 .
.
This is confirmed by a more rigorous analysis.
In an incentive-compatible equilibrium 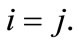 By means of Lagrange’s formula on finite increments, we can express the positive increment in borrowers’ expected utility, which would follow from an increase in the probability of receiving a loan, as
By means of Lagrange’s formula on finite increments, we can express the positive increment in borrowers’ expected utility, which would follow from an increase in the probability of receiving a loan, as
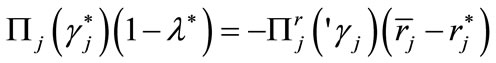 (11)
(11)
where 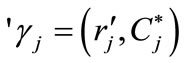 and
and 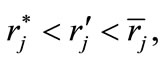

j = a, b, will denote the partial derivative of the type-j utility function with respect to r. Note that 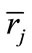 is the level of the rate of interest which absorbs all of the “surplus” ensuing from the increase in the credit probability;
is the level of the rate of interest which absorbs all of the “surplus” ensuing from the increase in the credit probability; 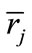 is a decreasing function of
is a decreasing function of 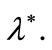
The increment in utility given by (11) will be partly offset by the increase in the rate of interest, which is required to yield a positive profit to a deviating bank. Employing again Lagrange's formula, the decrement in utility can be given as
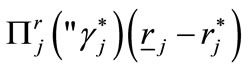 (12)
(12)
where 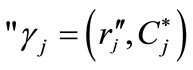 and
and 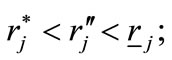
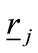 is the rate of interest fixed in the deviating offer. Clearly
is the rate of interest fixed in the deviating offer. Clearly  Then, a necessary condition for the existence of the sought deviating credit-offer is
Then, a necessary condition for the existence of the sought deviating credit-offer is
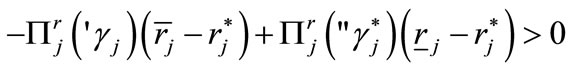 (13)
(13)
which reduces to
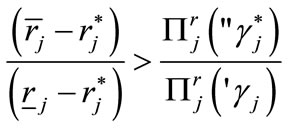 (14)
(14)
Obviously, the condition cannot be satisfied whenever.  However, the required inequality need not be satisfied even in the case of interest, that is when
However, the required inequality need not be satisfied even in the case of interest, that is when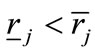 . In fact, the second order derivative of the expected utility with respect to the rate of interest has a uniform sign:
. In fact, the second order derivative of the expected utility with respect to the rate of interest has a uniform sign: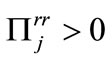 . This implies that
. This implies that 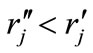 but then both members of inequality (14) are greater than one and we cannot tell whether this inequality is satisfied or not. Moreover, for values of
but then both members of inequality (14) are greater than one and we cannot tell whether this inequality is satisfied or not. Moreover, for values of 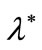 approaching 1 it can be demonstrated that the inequality is certainly violated.
approaching 1 it can be demonstrated that the inequality is certainly violated.
As regards this, consider that 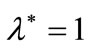 implies
implies  , while from
, while from 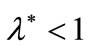 it follows
it follows 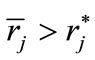 and
and  Moreover, when
Moreover, when 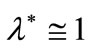 the left and righthand members of the inequality are approximately equal to one, because
the left and righthand members of the inequality are approximately equal to one, because 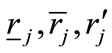 and
and  can be taken to be as practically coincident. Then, the effects of a decrease in
can be taken to be as practically coincident. Then, the effects of a decrease in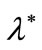 —in the neighborhood of 1—can be reckoned by means of the first-order derivative with respect to
—in the neighborhood of 1—can be reckoned by means of the first-order derivative with respect to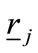 , valued at
, valued at 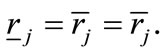 The effects on the left-hand and on the right-hand member of (14) are, respectively:
The effects on the left-hand and on the right-hand member of (14) are, respectively:
 (15)
(15)
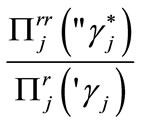 (16)
(16)
Both derivatives are negative, but observe that the modulus of the former is strictly greater than the latter, because 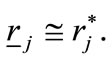 This proves that (14) is violated.
This proves that (14) is violated.
NOTES
1In the following, when we mention Bester without any further indication we imply reference to Bester [1].
2Bester [1], p. 851. On the definition of mean preserving spreads see Rothschild and Stiglitz [9].
3Convexity of the isoreturn curves holds when we consider both a continuous and a discrete random variable. On the contrary, Bester believes these curves to have mainly concave behaviour, which in turn implies that the expected utility is quasiconcave. See Bester [1], note 8, p. 851, and Figures 1 and 2 respectively at p. 852 and following. Standard renditions of this model employ concave isoreturn curves; cf. Goodhart [10] and Freixas and Rochet [11].
4Bester [1], p. 852 (“In the following, it will be assumed...”). Please note that assumption 2 would make no sense if borrowers were allowed to apply to a different bank for the remaining contract. Because they are not known, in this eventuality type a entrepreneurs would rather apply to a new bank for their preferred contract. See Figure 1 below.
5Bester [1], p. 852.
6Bester’s credit rationing is that of type II (see Keeton [12]), because some randomly-chosen borrowers obtain no credit at all, while the remaining ones get the required loan-size.
7The pooling isoprofit must not lie in the region that is delimitated by isoprofit α, indifference curve a, r-axis and contract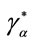 . Bester assumes this condition to be satisfied, see Bester [1], note 12, p. 853.
. Bester assumes this condition to be satisfied, see Bester [1], note 12, p. 853.
8See definition 1 given above, p. 3.
9An incumbent bank would earn a negative profit on type b borrowers. On the contrary, it could earn a positive profit on type a borrowers, but these won't demand this contract. See Bester [1], p. 853.
10In this case it suffices to apply our proof to the subgame consisting of the second stage of the credit market. The equilibrium is a subgame-perfect Nash equilibrium with rationing both at stage one and stage two of the credit market.
11For a definition of equilibrium rationing, see Jaffe and Stiglitz [13], pp. 847-849.
12For a definition of a contestable market see Baumol et al. [14].
13In any case, consider that an increase in N* will be partly offset by the consequent increase in the equilibrium rate of interest on deposits, and in the size of collateral costs as well.
14Stiglitz and Weiss [6] themselves implicitly adhered to Bester’s view, by considerably modifying their model in order to defend the possibility of rationing as an equilibrium phenomenon.
15Besanko and Thakor [4] and Bester [3], diverging partly from Stiglitz and Weiss [2], employ a perfectly elastic supply of deposits along with risk-neutrality. For their part, Stiglitz and Weiss [6] begin from a not-perfectly elastic supply of deposits and risk averse entrepreneurs.
16Here, the increase in the interest rate on deposits, which ensues to the deviant-bank offer, invalidates the proof of proposition 1.
17Part (i) of Assumption 1, see Gale [8], par. 7, pp. 221-223. Compare Figure 1 above.
18See Gale [8], p. 212 on the finite support of the allocation functions. In his environment, Gale claims the first part of his assumption 1 to be quite mild; ibidem, p. 222.

