ABSTRACT

In this paper, we study the optimal level of cash for the firm to hold. We model the cash level with inflows and outflows due to deposits and withdrawals; in between, the cash level is a stochastic process where it signals a time to sell. After modeling the continuous jump, we implemented first step analysis method to find the probability of the event with initial cash and we were able to calculate data driven by set of difference equations. These data are used to determine the length of the period of the investment. Then, we adopt the probabilistic decision model where it goes under mathematical optimization. This model let the investor to maximize the probability of success or to stop on one of the largest fortunes using the equation of the principle of optimality. Finally, to solve these optimal equations, we used the result of positive dynamic programming and we elaborated them by proves.

Keywords:

Cash Management, Markov Chain, Probability, Expected Duration, Mean Length, First-Step Analysis, Principle of Optimality, Positive Dynamic Programming

1. Introduction

Defining cash balance is a classic problem in firm’s financial management. Cash management happens due to the daily inflows and outflows. It has the following responsibilities: To mobilize, manage and plan the financial resources of business. Demand for cash can be positive or negative. Positive demand consists of accounts payable, whereas negative demand is known as account receivables. These funds are available at any moment in time for the firm.

Historically, cash management problem has been studied by various researches by extension of the continuous-review stochastic inventory models. These models were originally presented in Baumol (1952) [1] , whereby the author makes a parallel relation between cash with other firms’ inventories. Later Miller and Orr (1966) [2] presented a model that considers the assumption of random cash flows as the normal distribution. They consider only two assets, cash and an alternative investment. He adopted the uses of upper and lower bounds, and considering the small time gap between the investment of cash and withdrawing it. In this case, with buy and sell bond operations, they calculated the time on an hourly basis and the cost of maintaining the cash balance daily.

Since 1980’s, various authors have worked with the cash optimization problem which is divided into deterministic and stochastic process. In this type of research, Tapiero and Zuckerman (1980) [3] presented a stochastic model based on the premise that cash inflows and outflows have random behavior in a poisson process.

Considering the cash balance problem as a possible use of the general and stationary Markov Model in Hinderer and Waldmann (2001) [4] , the authors use a model for Markov chain processes in random environments that have a stationary process as, for example, low variation over time.

As the reader could notice, this subject is the main focus of many researchers over the past few decades, but because of the uncertainty related to receipts and payments from cash flow resources, what made the result a composition of random variables were implemented models with new approaches, mainly based on stochastic process. Further reading about history and origin of cash management are discussed in [5] .

Recently, a literature review was conducted similar to Newman’s (2002), which presented the Faustmann framework of optimal forest rotation literature in forestry investment decisions. The application of real options in forestry investment decisions developed during the late 1980s from the simple topic of nature preservation employing a quasi-option value. This analysis method has recently been applied to much larger problems of timber cutting contracts employing Monte Carlo simulation approaches. In addition, geometric Brownian motion and mean reversion, two of the most prevalent continuous-time stochastic price models, are discussed. The number of publications slowly but steadily increased from the early 1980s to the late 1990s and has remained steady since the early 2000s, with an average of 2.7 articles annually. The discounted cash flow technique remains the major tool supporting forestry investment decisions.

The study conducted by Yao et al. (2006) [6] presents a different formulation, considering the demand for money according to fuzzy logic concepts, developing a single period model as, for example, without using past data due to historical data not being able to provide a cash demand forecast. Along these lines of stochastic development, Volosov et al. (2005) [7] present a stochastic programming model in two stages, based on scenario trees, which consider not only the problem of cash balance, but also the exposure to international currency, addressing the risk of exchange rate variation. In this model, the authors consider cash flows coming from different currencies, relating to the aspect of existing foreign exchange and the need for hedging. Thus, the authors obtain positive results in determining the optimal cash balance. More recently, Gormley and Meade (2007) [8] have differentiated their work by presenting a dynamic policy for cash balance that minimizes transfer costs when cash flows are not independent or identically distributed in a general cost structure. By using this methodology, the authors used historical data to develop a time series model to forecast cash flows, promoting a conditional expectation of future cash flows and obtaining results in the reduced transfer cost.

Melo and Bilich (2011) [9] propose the use of dynamic programming to minimize the cost of cash, considering the cost de rupture cash. In order to ensure that investment decisions are made optimally in terms of both reward and risk, suitable frameworks for the solution of supply chain optimisation problems under uncertainty are required. Most of the existing frameworks are suitable for two-stage problems while there is a need for appropriate multi-stage, multi-period optimisation frameworks for supply chain management as Balasubramanian and Grossmann (2004) [10] and Wu and Ierapetritou (2007) [11] .

In this manuscript, we consider an inventory approach to cash management where the stochastic nature appears in the demand for money.

2. Model

The firm’s cash level fluctuates randomly as the result of many relatively small transactions. We model this fluctuation by dividing time into successive, length periods and by assuming that from period to period, the cash level moves up or down one unit, each with different probability.

Using these symbols, we will elaborate our study by letting:

s: Minimal capital.

S: Maximum capital.

n: Period n or cycle.

p: Probability of success.

q: Probability of loss.

$T_0$ : Initial cash on hand.

$X_n$ : Event when the cash reaches the boundaries at n^th periods.

T: Random time of the first transaction when it stops at 0 or S.

$T_0+1$ : First position when there is successful investment.

$T_0-1$ : First position when the investor loses his investment.

k: Possible cash states.

$u_k$ : Probability of cash fluctuation starting from initial state k.

$s+1$ : State at first step of success.

$s-1$ : State at first step of loss.

$W_{s+1}$ : Remainder after the first step of success.

$W_{s-1}$ : Remainder after the first step of loss.

$W_s$ : Mean duration starting from s reaching k.

$W_s^h$ : Homogeneous solution of mean duration.

$W_s^p$ : Particular solution of mean duration.

$W_{sk}$ : Expected number of visits to level k starting from s.

$1\left\{X_n=k\right\}$ : Indicator random variable that takes value 1 when it reaches k and the value 0 otherwise.

$\max \left(s-k,0\right)$ : Maximum state k reached between 0 and s.

r: Total cost of holding cash on hand during a cycle.

K: Fixed cost of each transaction.

$T_i$ : Duration of the i^th cycle.

$R_i$ : Total opportunity cost of holding cash on hand.

$Y_n$ : Maximum value observed in the sequence of $Y_1$ till $Y_n$ .

${\sigma }_i^{\mathrm{<mo>\; *\; </mo>}}$ : Optimal stopping time.

$P\left\{Y_{{\sigma }^{\mathrm{<mo>\; *\; </mo>}}}\right\}$ : Probability of success where the investor will stop investing with the largest fortune.

C: All stopping time.

$w\left(x\right)$ : Probability of success starting from x.

$s\left(x\right)$ : Probability of success starting when the firm stop in x.

$c\left(x\right)$ : Probability of success when firm continue investing in an optimal manner.

$x^{\mathrm{<mo>\; *\; </mo>}}$ : Valid investments at state x.

x: Set of fortune valid at state x.

f: Stationary policy.

$x\mathrm{<mo>\; <\; </mo>}{x}^{\mathrm{<mo>\; *\; </mo>}}$ : State when the firm stop investing.

$x\ge x^{\mathrm{<mo>\; *\; </mo>}}$ : State when the firm continue investing.

$w_f\left(x\right)$ : Probability of success starting from state x when policy f is employed.

$P_x$ or $P_x\left(S-x\mathrm{,}x\right)$ : Probability reaching the fortune at state x before the maximum amount of capital S.

i: Largest fortune that the investor feels satisfied about.

r (Section 2.4.2): State of when the investor chooses to stop.

$P_x\left(i\mathrm{,}x\right)$ : Probability of success at state x having one of the largest fortune i.

$k_i^{\mathrm{<mo>\; *\; </mo>}}$ : Valid investment at i when the firm stops at one of the largest fortune.

We consider cash management strategies and we specify cash levels by two parameters, s and S, where $0<s<S$ . The policy is as follows:

-When the firm’s capital drops to zero, then he will sell sufficient bonds to replenish the cash level up to s.

-When it increases up to S, then the investor will invest in treasury bills in order to reduce the cash level to s.

This process has led us to adopt an approach in [12] to analyse fluctuation.

We see in Figure 1 that the cash level fluctuates in each cycle when it begins with s units of cash on hand and end at the next intervention whether a replenishment or reduction in cash.

We will begin our study by evaluating the mean number of visits to a

particular state, the mean length of a cycle, first step analysis and at the end we will evaluate the long run performance of the model.

Consider a firm who wins or loses on each investment as a result of many small deposits and withdrawals. We model this fluctuation by dividing time into periods. In each time period, assume the reserve randomly increases one unit of cash with probability p and decreases one unit by a probability q.

We will model this assumption using stochastic probability where $p\ne q$ . Let’s define the random variable $Y_1,Y_2,\cdots$ where

$Y_n=\{\begin{array}{ll}+\mathrm{1,}\hfill & \text{with}\text{probability}p\mathrm{<mo>\; ;\; </mo>}\hfill \\ -\mathrm{1,}\hfill & \text{with}\text{probability}q\mathrm{.}\hfill \end{array}$

We start with an initial value $T_0=Y_0=s$ as initial cash. We define the

sequence of sums $T_n={\displaystyle {\sum }_{i=0}^n}{Y}_i$ which makes the sequence $T_n=T_0+{\displaystyle {\sum }_{i=1}^n}{Y}_i$ is

the cash on hand at period n. We can look at how many investment the process will experience until it achieves 0 or S. Each investment is of probability p and $q=1-p$ respectively.

3. Probability and Mean Duration

Let T denote the random time of the first transaction and $X_n$ represents the event when they both reach 0 or S at n^th period.

In symbols, $T=\min \left\{n\ge 0;X_n=0\text{or}{X}_n=S\right\}$ . If there is success the firm continues to invest as if the initial position is $T_0+1$ with probability p and if the firm loses the position initial is $T_0-1$ with probability q.

$T_0+1$ and $T_0-1$ are the first trial when the firm invest. That’s why the most important step in real life phenomena is the first step analysis. Its main benefit is that it provides a benchmark to evaluate more methods. To this end, we perform the first step analysis associated with our optimization problem by:

The Method “First-Step Analysis”

The probability of the cash fluctuation starting from the initial state k is:

$u_k=Pr\left\{X_T=\mathrm{0\; <mo>\; /\; </mo>}{X}_0=k\right\}$

where the event written as $X_T=0$ is the event of firms robbed.

Similar to the first step analysis in [13] and [14] we will obtain the equations

$u_k=p{u}_{k+1}+q{u}_{k-1},\text{for}k=1,2,\cdots ,S-1.$ (1)

with boundary conditions:

$u_0=1,u_S=0.$

We begin the solution by introducing the differences $x_k=u_k-u_{k-1}$ for $k=1,2,\cdots ,S$ . Using $p+q=1$ to write $u_k=\left(p+q\right)u_k=p{u}_k+q{u}_k$ , equation (2.1) becomes:

$k=1;0=p\left(u_2-u_1\right)-q\left(u_1-u_0\right)=p{x}_2-q{x}_1;$

$k=2;0=p\left(u_3-u_2\right)-q\left(u_2-u_1\right)=p{x}_3-q{x}_2;$

$\cdots$

$k=S-1;0=p\left(u_S-u_{S-1}\right)-q\left(u_{S-1}-u_{S-2}\right)=p{x}_S-q{x}_{S-1};$

given,

$x_2=\left(q/p\right)x_1;$

$x_3=\left(q/p\right)x_2={\left(q/p\right)}^2{x}_1;$

$x_4=\left(q/p\right)x_3={\left(q/p\right)}^3{x}_1;$

$\cdots$

$x_k=\left(q/p\right)x_{k-1}={\left(q/p\right)}^{k-1}{x}_1;$

$\cdots$

$x_S=\left(q/p\right)x_{S-1}={\left(q/p\right)}^{S-1}{x}_1;$

Now, using $u_0\mathrm{,}{u}_1\mathrm{,}\cdots ,u_S$ by invoking the conditions $u_0=1,u_S=0$ and summing the $x_k$ ’s:

$x_1=u_1-u_0=u_1-1$ ;

$x_2=u_2-u_1$ , $x_1+x_2=u_2-1$ ;

$x_3=u_3-u_2$ , $x_1+x_2+x_3=u_3-1$ ;

$\cdots$

$x_k=u_k-u_{k-1}$ , $x_1+x_2+\cdots +x_k=u_k-1$ ;

$\cdots$

$x_S=u_S-u_{S-1}$ ,;

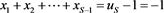The equation for general k gives:

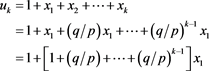(2)

which expresses 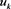in terms of; But 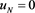gives

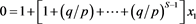
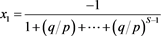
which substituted into (2.2) gives:

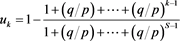
The geometric series sums to:

whence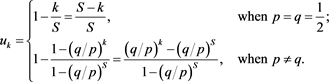

A similar approach can be used to evaluate the mean duration, the time T is composed of a first step plus the remaining steps. With probability p, the first step of success is to state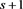, and then the remainder is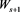.With probability q, the first step of loss is to 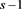and there are 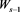remainder.

Thus, for the mean duration, a first step analysis leads to the difference equation:

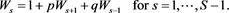(3)

The firm will end its investment in states 0 and S.

The boundary conditions are:.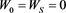

We will solve (2.3) when: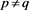

First, we need to find the general solution to the homogeneous equation:

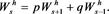
and a particular solution to the non-homogeneous equation.

We already know the general solution to the homogeneous equation:

which is:

Then, we use the form to find the particular solution. and E represent the constants to be found that fits and to obtain, the general solution.

The general solution of the duration equation is:

The boundary conditions require that, and

.

Solving for A and B, we find:

(4)

Comparing to Dunbar’s paper [15] where he discussed the following:

If; the particular solution is. It follows the general solution is of the form; satisfying the boundary conditions the solution is.

4. Mean Number of Visits to a Cycle

Now, fix a state k where and let be the expected number of visits to the level k starting from s given by a formal mathematical expression which is:

where is the indicator random variable that takes the value 1 when reaches state k and 0 otherwise.

Note that if I go to a bank N times and is the event (“I am robbed the n^th

time”) then the inner sum “” is the total number of times where I am

robbed.

Then using the first step analysis, satisfies the equations:

(5)

with boundary conditions

where

We consider two cases:

• case 1: When, we will obtain the homogeneous equation;

• case 2: When, we will obtain a non homogeneous difference equation.

Using Linear Algebra, we found the particular solution:

Following that:

which makes the full solution when is as following:

where we denote by the notation

so when; we will obtain:

Using the obtained result of, the mean total unit periods of cash on hand up to time T starting from, multiplying by k, by r and summing overall the cash is calculated as follow:

(6)

These results are interesting and useful in their own right as estimates of the length of a cycle and the expected cost of cash on hand during a cycle. Now we use these results to evaluate the long run behavior of the cycles. These cycles are statistically independent. Let K be the fixed cost of each transaction. Let be the duration of the ith cycle and let be the total opportunity cost of holding cash on hand during that time. Over n cycles the average cost per unit time is:

Next, divide the numerator and denominator by n, we obtain :

Let r denote the opportunity cost per time unit of cash on hand. Then, while. Since these quantities were determined in (2.4) and (2.6) respectively we have:

(7)

We used calculus to determine the minimizing values for S and s, it simplifies matters if we introduce the new variable. Then (2.7) becomes:

Take the partial derivatives with respect to x and S and set them equal to zero, then solve, to find the critical points.

and

Implementing the cash management strategy with the values and results in the optimal balance between transaction costs and the opportunity cost of holding cash in hand.

In our study, we adopted the approach with as oppose to what in literature used to solve the optimization problem where they used similar probabilities when. Dunbar specifically worked on where he found

and, the probability of cash fluctuation and the mean

duration respectively. Our approach is more realistic because there is no similar probabilities in real life. Contrarily to their study too, we analyzed the first step analysis. At the end, we evaluated the long run behavior cost. The last one is better than the short one because the firm will have the flexibility to change big components to achieve optimal efficiency.

5. Optimal Stopping Time

5.1. Maximize the Probability of Success

In the previous section, we discussed when the firm will go bankrupt or when it reaches a predefined boundary. Now, we will discuss the decision that the investor will take to stop or continue investing [16] [17] .

This decision-making problem is classified under two categories: deterministic and probabilistic decision models. During our work, we will adopt the probabilistic decision model where it goes under the mathematical optimization. It is the branch of the computational science that seeks the answer to the question “What is the best?”. The model of the mathematical optimization consists of an objective function and a set of constraints expressed in the form of a system of stochastic inequalities [18] .

Optimization models are used in almost all areas of decision making such that financial investment and cash management. The process of these models starts by describing the problem; prescribes a solution and controls the problem by updating the optimal solution continuously while changing the parameters.

5.2. Optimization’s Model

The sequence defined in Section 2.1 as a sequence of random variables is redefined in this section. Then, the serious decision of either to stop or continue takes place at time n when is the maximum value observed.

The sequence is now defined as follow:

The objective is to find a stopping policy that will maximize the probability of success where the investor will stop investing with the largest fortune. This problem can be described in terms of stopping time as that of seeking an optimal stopping time such that:

(8)

where C is all stopping times and T is the time process defined in section 2 as:

.

This decision state is referred to as state x if, because the decision depends neither on the values of nor on the number of investments already made.

Let be the probability of success starting from state x, and let:

• be the probability of success when the firm stop in state x

• be the probability that the firm continue investing in an optimal manner in state x.

Then, the principle of optimality:

(9)

where is already defined by in Section 2.2.1:

(10)

and

(11)

as given in [16] [17]

with the boundary conditions:

To solve the optimality equation we use the result of positive dynamic programming [19] . If the result fits the framework of the positive dynamic programming, then a given stationary policy is optimal if its value function satisfies the optimality equation. This problem fits the framework of positive dynamic programming since if we suppose that the reserve increases one unit of cash if we attain the largest over all and all other reserves are zero, then the expected total fortune equals the probability of success.

Let f be a stationary policy which, when the decision process is in state x, chooses to stop if and only if where:

(12)

Then f is optimal.

belongs to the set of valid investments and x belongs to the set of fortune.

In addition, because we will always assume that the investor cannot invest using the capital that he doesn’t have and doesn’t invest more than he needs in order to reach the target;

To prove that f is optimal when (2.12) is considered:

Let denote the probability of success starting from state x when policy f is employed.

Once the decision process leaves state x; i.e.; it never stops until absorption takes place under f.

We obtain:

(13)

where

(14)

Observe that is decreasing in x because if we find the derivative of (2.10):

;

we obtain:

which will be negative. For that is decreasing in x.

Similarly, the derivative for, is and it is negative

that’s why we say that is decreasing in x. While is increasing in x because if we find its derivative, we find that.

In fact, from Equation (2.14) and

for:

For,.

Let’s prove that f is optimal where f is as defined in (2.9). We have to show that and satisfies:

(15)

as given in [16] [17] ; and

(16)

we have to work on the conditions where and;

1) for; it means when;

(17)

or

Then,

Let’s verify the inequality for:

In this case,

-

-

-

(18)

True, so the inequality is verified.

Now, for:

-

-

-

-

-

So the inequality is as follow;

(19)

2) Check for:

It means that when;

(20)

or;

Let’s start with:

for

and so,

Having;

To prove that the investor will continue investing, we have because P denotes the probability of success starting at state x and when the firm stop at state x. The inequality (2.20) is proved for, so the inequality is proved and makes the statement true for.

5.3. Optimal Stopping Time of Satisfaction

In this section, we will find an optimal stopping time of when the investor feels satisfaction and stop investing on one of the largest fortune that he had.

Similarly to the previous section, the optimal stopping time is given by:

(21)

where:

(22)

We denote the serious decision as if:

.

This state can be written as if where and and

Let where be the probability of success starting from state and and as defined in the previous section.

The principle of optimality is:

(23)

where

when

with

(24)

and;

(25)

Similarly;

Let f be a stationary policy which, when the decision process is in state; we chooses to stop if and only if where:

(26)

Then f is optimal.

Let’s prove the Equation (2.26);

Let be the probability of success starting from state when the policy f is employed.

Once the decision process leaves the state for it never stops until absorption takes place under f.

(27)

is decreasing already proved; while is increasing in x, and is given as follows:

we choose to continue in state; if.

It means that for:;

Let

(28)

to show that; we have to show:

(29)

so let’s substitute each variable by it’s convenient expression in (2.29) we obtain;

(30)

Having;

simplify by we will get;

(31)

So, the inequality for is proved.

5.4. Conclusions

Managing the cash balance is important in business administration, but rarely do we apply the techniques presented in this study in practice. Much of this neglect is due to the difficulty in developing models closer to reality. Despite its name, optimization does not necessarily mean finding the optimum solution to a problem. Furthermore, the view of the cash balance is still limited and not regarded as an investment, which has a negative profitability defined by total cost of the cash, immediate liquidity, and risk associated with cash deficit. Thus, it is necessary to understand the cash balance together with other financial investments and examines the investment choices in financial products.

This is a classic problem in business, involving economics, accounting, and finance, and it should return to be the focus of discussions in these areas, as the existing limitations concerning the models and methods can be eliminated. We must discuss the cash balance problem not only about the method involved in optimization but also in practical application. Further studies can be done concerning the elaboration of this topic and discussing the fair investment when there is no loss or gain during investment. Finally, we must discuss the cash balance problem not only about the method involved in optimization but also in practical application.

Cite this paper

Dib, Y.M., Kmeid, N., Greige, H. and Raffoul, Y.N. (2018) Optimization of Cash Management Fluctuation through Stochastic Processes. Journal of Mathematical Finance, 8, 408-425. https://doi.org/10.4236/jmf.2018.82026

References