ABSTRACT

This paper studies the impact of dry markets for underlying assets on the optimal stopping time and optimal exercise policy of American derivatives. We consider that the underlying is transacted at all points in time except for a subset of dates, for which there is an exogenous probability that trading may exist. Using superreplicating strategies, we derive expectation representations for the range of arbitrage-free values of the derivatives. For arbitrary probability, an enlarged filtration jointly induced by the price process and the market existence process makes ordinary stopping times sufficient to characterize such representation. For the deterministic case where the probability is zero, randomized stopping times are required. Several comparisons of the ranges obtained with the two market restrictions are performed. Finally, we conclude that market incompleteness caused by dryness may delay the optimal exercise of American derivatives.

Keywords:

Option Pricing, Incomplete Markets, Dry Markets, Optimal Stopping Time, Randomized Stopping Time

1. Introduction

Derivatives were originally priced by assuming that markets were complete, computing the value of a derivative as the value of a self-financing, and replicating portfolio on the underlying risky asset and risk-free bond. Such portfolio could be rebalanced by continuously trading the underlying asset and bonds. The value of the initial portfolio could be shown to be the no-arbitrage price of the derivative. In the case of American derivatives, Karatzas [1] has shown that, in this complete market setting, the no-arbitrage value of one such derivative is indeed the supremum of the implied European derivative values over all possible stopping times. In the presence of market imperfections, such simple assumptions do not hold and markets become incomplete, making the pricing mechanism of options more subtle. In particular, it may be difficult to characterize the rebalancing portfolios. This issue has become a major concern for financial economists since real markets are not perfect, and a significant literature about option pricing in incomplete markets has been developed1.

In this paper we assume that an American derivative and its respective underlying asset may not be traded at some points in time, generating incomplete markets, and then study the impact of this constraint on its optimal stopping time. In particular, we show that this incompleteness may delay the optimal exercise of American derivatives as compared to the case of complete markets. We are also able to write upper and lower bounds for their possible non-arbitrage values in terms of both randomized and ordinary stopping times.

The market for an asset is said to be liquid when there are numerous buyers and sellers, making a quick trade easy to be executed. In such circumstances, variations in supply and demand should not have a significant impact on the transaction price. An illiquid market implies that it may not be that easy to sell or to buy the asset. The fact that the underlying asset can be traded only at some points in time can be described as a particular lack of liquidity of the market, as in [10] . We shall refer to this situation as dry markets. We will consider the deterministic case, when we know ex-ante at which points in time markets do exist or do not exist and the probabilistic case, when we assign a probability p to the existence of the market at each point in time. Lack of liquidity is of extreme practical importance. It suffices to think about how many hours per day the exchanges are closed and stocks cannot be traded. Even while exchanges are open, there is strong empirical evidence (see [11] among others) of heavy trading at the beginning and the end of the trading day and relatively light trading in the middle of the day. Such U-shaped pattern of the average volume of traded shares reflects the fact that markets are essentially dry away from opening and closing hours. A rich literature modeling the nature of such intraday dryness for stock markets emerged with [12] [13] , and expanded to many other markets such as the FX markets [14] . Other examples where trading is not possible include refracting periods for swing options and vesting periods for employee stock options.

Markets’ dryness implies that markets become incomplete in the sense that perfect hedging of the derivative in all states of nature may no longer be possible. However, for any given derivative, portfolios can be found that have the same payoff as the derivative in some states of nature and higher payoffs in the other states. Such portfolios are said to be superreplicating (or superhedging). Holding one such portfolio should be worth more than the derivative itself and therefore, the value of the cheapest of such portfolios should be seen as a bound on the value of the derivative. The nature of the superreplicating bounds for European derivatives was well characterized in the context of incomplete markets by [2] [3] [4] [5] . Under market incompleteness, the hedging position of a market-maker depends on whether this intermediary is in a long or in a short position. This fact results in a lower and an upper bound for the derivatives’ values. The superreplicating bounds establish the range of prices outside which an investor has a positive profit with probability one. In other words, an arbitrage opportunity exists if the investor sells options above the upper bound or buys options below the lower bound.

There has been a relatively extensive literature characterizing in varying degrees of generality the superreplicating bounds of American derivatives in incomplete markets such as in [6] [7] [8] [9] . A later paper by Chalasani and Jha [15] discusses the particular case of transaction costs in discrete time and concludes that, in their specific setting, the superreplicating bounds of one such derivative may also be written as the supremum of the implied European derivative value. However, there are two important subtleties in their result: first, the supremum must be taken over randomized stopping times and second, the probability measure defining the European value over which the supremum is taken, may depend itself on the randomized stopping time that solves the problem.

The results of these authors were related to the fact that², under incomplete markets, the choice of exercise policy may influence the characterization of the marketed subspace, and therefore influence the pricing of securities. A rational exercise policy may even not be well defined if the state-price deflator depends on the exercise policy. This is their argument for using optimal randomized stopping times when characterizing the superreplication bounds of American derivatives under proportional transaction costs.

We contribute to this literature by showing that in the case where market incompleteness is generated by dryness, the supremum may be taken over usual deterministic stopping times, as opposed to the randomized stopping times in [15] . We are also able to understand how to recover their result in the dry market context, contributing to a better understanding of the process of exercising American options in incomplete markets. In that sense, our results extend their results and imply that the nature of the optimal stopping time may depend on the imperfection mechanism generating market incompleteness. Although the result for deterministic dry markets may be understood in the context of superreplicating bounds, as discussed heuristically in [17] , the case of probabilistic dry markets is of a different nature, since it crosses an additional source of uncertainty (existence or non-existence of underlying trade at any given point in time). We are thus allowed to conclude that the need of randomized stopping times clearly depends on the nature of the market incompleteness. In order to be perfectly comparable with the previous literature, our results are developed in a discrete-time setting, and use well-understood techniques such as backward induction and linear-programming duality, available without any technical difficulties. On the financial side, liquidity and the lack thereof are important issues that are modeled according to this discrete-time setting, allowing for quite intuitive conclusions.

Furthermore, under some regularity conditions, in dry markets the choice of exercise policy does not affect the characterization of the marketed subspace. Actually, we are able to show that this type of market incompleteness may delay the optimal exercise of American derivatives as compared to the case where the underlying asset may be traded at every point in time.

Our work is organized as follows. Section 2 presents the model and relevant probabilistic concepts, after which Section 3 presents the results for the upper and lower superreplicating bounds of American derivatives. In Section 4 these different bounds are compared. The exercise policy in dry markets is discussed in section 5. Finally, in Section 6 we conclude. Our main technical proofs are presented in the Appendix.

2. Dry Markets

2.1. The Model

In this paper we shall follow the notation used in [15] making it easier to compare the techniques and the results of both papers. Consider an economy where three different assets are traded. There is a risk free asset with unitary initial value providing a deterministic total return of 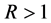per period; there are also a risky asset and a third asset, an American derivative, written on the risky asset, with expiration date T. The discrete set of possible transaction dates is denoted by 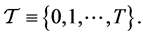The value of the underlying risky asset over time is modelled by means of a finite event tree, each node being identified by a pair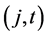, where j denotes the j-th node at time t. There is only one node at time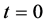, denoted by 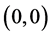For any given node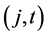, the set of successors at time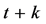, , 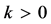is denoted by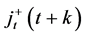. For simplicity let 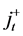denote the set of immediate successors, i.e.,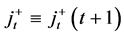. The nodes 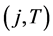are called terminal nodes and 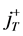is assumed to be the empty set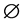. We also assume that, for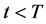, each node 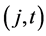has a nonempty set of immediate successors, i.e.,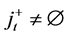. In an analogous way, the set of immediate predecessors of a node 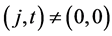is denoted by. In what follows we shall consider the case where such sets have a unique element. Moreover, we denote by the set of all nodes at any point in time t.

A path on the event tree is a set of nodes such that each element

in the union satisfies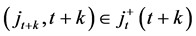, with and. Let denote the set of all paths on the event tree. Each node in the tree represents the set of all tree paths that contain that node. Let denote the price of the risky asset at node. A natural filtration on the space associated to the price process S is, where each is, the s-algebra generated by the observed realizations of random prices S until t. All the random variables will be defined in the measurable space. Similarly, let G denote the process followed by the payoff of American derivative. Hence, denotes the payoff of the American derivative at node whenever exercised at that point. Let and stand for the discounted values of the above processes, i.e.,

Dry markets are characterized by the fact that transactions are possible with probability one only at some points in time t in a set. It is also assumed that transactions are always possible at times and, i.e.,. Similarly, let be defined as the set of points in time such that transactions are possible, but not necessarily certain. For each, we assume that transactions are possible with an exogenous know probability (the same for every), with and. We distinguish the case (where the dry nature of the markets is deterministic) from the case where, (where dryness is probabilistic). In the case where, markes are liquid and complete.

We can think of the existence (or not) of trade at time t as the realization of a random variable. This random variable is defined for all and is assumed to be independent of the ordinary source of uncertainty that generates the price process. We can therefore talk about a trade existence process. In order to construct one such process, let us first start with the state space. Let denote the number of points in. At each of these points, trade may either exist or not, leading to possible states of nature. The collection of possible states of nature is denoted by, each corresponding to a distinct state. We now consider the new extended mea- surable space, where

and the enlarged filtration

with, where is, the s-algebra generated by the observed realizations of the random variable y until t. The random variable assumes the values 0 (when there is no trade) and 1 (when there is trade) and is not dependent on the price path w. We assume that there is a probability measure, such that for all, we have and. Similarly, for all, and Let the dimensional vector denote a given realization of the process. There are different possible vectors. In the presence of dry markets the risky asset’s price process S is only observed when trade exists, i.e., in nodes such that. This means that if at t, then.

2.1.1. The Liquid Case and the Perfectly Replicating Portfolio

When, markets are complete and the value of an American derivative is known to be the value of the cheapest self-financed portfolio3 on the underlying risky asset and risk-free bond that exactly replicates the payoff of the American derivative⁴. In that case, consider at any node the portfolio constituted by shares of the underlying asset and an amount invested in the bond. Such portfolio is denoted by and its value process is given by

Under the absence of arbitrage, the initial value of the derivative coincides with if, for any two consecutive transaction times and, the following condition holds at any non-terminal node:

2.1.2. The Dry Markets Case and the Superreplicating Portfolios

When markets are dry the number of traded securities at some points in time may not be sufficient to allow the construction of a self-financing replicating portfolio. Markets are then said to be incomplete. In that case, there is not a unique arbitrage-free value for the American derivative. By replacing the notion of replicating strategy by the notion of superreplication strategy it is possible however to derive an arbitrage-free range of values for the American derivative.

We now focus on the construction of the admissible superreplicating strategies for probabilistic dry markets. At any point in time, the number of shares and the amount invested in the risk-free asset will depend on the existence, or inexistence, of trade at the previous moments in time. However, these values will not depend on the future existence of trade.

Let and B denote, respectively, the number of shares and the amount invested in the risk free asset at node. We assume that, if and is an arbitrary successor of, then

and,

since the portfolio cannot be rebalanced at time t. In that sense the admissible trading strategies will depend on the last point in time where trade occured. For that reason we shall use the notation and for any given realization, , of the process . Hence, for any given two different sets and with common values up to time t, we assume

Just as in the deterministic case, let denote the value process generated by such portfolio, i.e.,

Hence,

In an analogous way to the deterministic case, the definition of self-financed strategy and superreplicating strategy is dependent on whether one is in a short or in a long position in the derivative.

In what follows we characterize the upper and lower arbitrage-free bounds for the value of the American derivatives in the described framework. In order to do that, we first define some necessary mathematical objects in the following section.

2.2. Some Probabilistic Definitions

In this section we adapt to the case of dry markets some definitions and results from [15] and required to obtain the arbitrage-free bounds of an American derivative. We begin by defining as the subset of points in after the last non-trading date. Formally we define with

Notice that and for liquid markets.

Definition 1. A node probability measure is a nonnegative function satisfying

(1)

Let denote the set of all node probability measures.

Definition 2. A node probability measure is said to be a node mar- tingale measure if, for any and such that, satisfies

The martingale term is justified in the sense that under that measure, for given, all for can be replaced by, provided they are multiplied by the respective martingale measure. The set of all node martingale measures is denoted by.

Definition 3. A node probability measure on the event tree is said to be y-simple if, for each, any t and, there are no two nodes in the same path, say and such that and where is any set such that

The following theorem is analogous to Theorem 6.7 in [15] adapted to dry markets.

Theorem 1 (Chalasani and Jha) The extreme points of the set are simple node probability measures, i.e., on every path on the event tree there is at most one node where q is strictly positive.

Proof. Theorem 6.7 in [15] can be extended to the case of deterministic dryness. In the general probabilistic case, it suffices to consider the auxiliary node probability measures which, for any y, are defined for all and. By construction for and for all. The result follows straightforward by applying the extension of Chala- sani and Jha’s result to the measure.

Definition 4. An adjusted probability measure is a nonnegative function defined for any and with such that and

with

Let the set of all such probability measures be denoted by. Also, let denote an ordinary stopping time that is conditional on the realization of the process. For any, is a map that is defined from to such that for all. Moreover, consider that for two different sets and with common values, up to time t, if, where, then. A set of stopping times, one for each, satisfying the abovementioned property is denoted by, i.e.,

Consider. We define a nonnegative -adapted process associated with the stopping time that has the form if and otherwise. Let and denote the set of all and associated, respectively.

Definition 5. A y-simple node probability measure is said to be associated with a given stopping time if is equal to zero when is equal to zero, and is positive when is strictly positive, for any and node.

Let the set of all node probability measures with this property be denoted by.

Definition 6. For any probability measure and stopping time we say that is a -martingale measure if, -almost surely, for any and such that we have

The set of all that have this property is denoted by. Let denote a measure-strategy pair, i.e., a pair constituted by an adjusted probability measure and a nonnegative adapted process.

Definition 7. A measure-strategy pair is said to be equivalent to a node probability measure if, for any given node with,.

We can now enunciate the following result, adapted from [15] to include the random variable y.

Theorem 2. Consider a node probability measure Then there exists a measure-strategy pair equivalent to q, where for any given, and are uniquely defined at node where

is strictly positive. Conversely, if is a measure strategy-pair, then the node function such that is the unique equivalent node-measure.

Proof. Consider that the auxiliary node probability measures, , and the auxiliary adjusted probability measures, and are also defined for all. By construction, for all and for all. Applying the result of corollary 5.5 in [15] we find that

and, for all

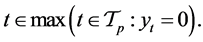
The mathematical definitions provided above are dependent of y. In what follows we show that it is possible to define an adjusted probability and a randomized stopping time in the original tree related with the concepts just presented.

Definition 8. An adjusted probability measure is a nonnegative function such that and, for all.

The set of all such probability measures is denoted by.

A randomized stopping time is a nonnegative -adapted process X with the property that on every path of the event tree the sum of the random variable is equal to one, i.e.,

(2)

where. The set of all randomized stopping time is denoted by.

Definition 9. For a given randomized stopping time, an adjusted probability measure is said to be a -martingale measure if there are a stopping time and a -martingale measure such that

for any with.

Let denote the set of all that are martingale measures.

Theorem 3. For any given stopping time and -martingale mea- sure, there is a randomized stopping time and an -mar- tingale measure, which are defined as follows. Just for notation sake, let us consider

with The adjusted probability measure is such that and, for any such that,

If then for a given successor of and is zero for all others successors of.

The randomized stopping time is uniquely defined for any node such that and is given by

If but there is a predecessor such that take

Otherwise,.

Proof. See Appendix.

3. Results on Dry Markets

3.1. Upper Bound for the Value of an American Derivative

The upper bound for the value of an American derivative (also called its upper hedging price) is the maximum value for which the derivative would be traded without allowing for arbitrage opportunities. Such upper bound coincides with the value of the cheapest self-financed portfolio that the seller of the derivative can acquire in order to be completely hedged against any possibility of early exercise of the American derivative.

A strategy is said to be self-financed if, for any given, the portfolio at node, where, generates at a value such that

(3)

with and

A sequence of portfolios, one for each, is said to be a

superreplicating strategy if the value of each portfolio is higher than or equal to the payoff of the derivative at any node in the next transaction time. In other words, for any trading dates t₁ and t₂ such that and and arbitrary nodes, and, the portfolio at t₁, , must be such as to generate in t₂ a value such that

(4)

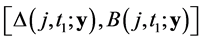
Since the upper bound is the value of the cheapest initial portfolio, it must satisfy

where the decision variables are the and for all non-terminal nodes, this optimization is subject to the self-financing and superreplication constraints (3) and (4).

More formally, for any given take any such that. Define the con- secutive trading date t₂ as. The upper bound for the value of the American derivative can thus be seen as the solution of the following problem:

subject to the superreplicating constraints:

(5)

(6)

and subject to the self-financing constraints:

(7)

for any.

Using results from linear programming the upper arbitrage-free bound of the American derivative can be written as follows.

Theorem 4. The upper hedging price of an American derivative in a probabilistic dry market can be written as

Proof. The proof follows from characterizing the dual of the linear programming problem above characterizing. Full details can be obtained from the authors.

The upper bound solving the problem above can also be seen to be the solution of a more intuitive problem. In fact, it can be shown that this upper bound maximizes over all possible stopping times the expected discounted payoff, when the expectation is optimized among all adjusted probability measures. In other words,

Theorem 5. The upper hedging price of an American derivative in a probabilistic dry market can be written as

where

Proof. Using Theorem 1 and Theorem 2 the conclusion is straightforward.

Note that this result is the same that would be obtained if the filtration describing the risky asset price is augmented, with no uncertainty about the existence of trade and no trade in some nodes. Using this filtration, ordinary stopping times are sufficient to write the upper bound as an expectation.

However, the upper bound on the value of an American derivative can also be written using randomized stopping times under an adjusted probability measure. The adjusted probability measure must be decomposed in such a way that, if an augmented filtration is considered, the risky asset price is a martingale. Under the original filtration it is not possible to write the upper bound as an optimization over ordinary stopping times as in the former Theorem. In this case randomized stopping times may be required.

Theorem 6. The upper hedging price of an American derivative in a probabilistic dry market can be written as

with

Proof. In order to prove that the optimum value determined by the optimization problems in Theorem 6 coincides with the one presented in Theorem 5, we notice that

(8)

We then establish a relation between the two sets over which the optimization problems presented in both theorems are performed. We begin by considering an element of. By Theorem 3 and the implication presented in Equations (8),

for any element of, there exists an element that belongs to

, such that. Now, consider an element of.

By the definition of a -martingale measure and, once again, by the relation pre- sented in Equations (8), for any element in there exists an element in such that. Hence, given the relation established between the two sets the values determined by the two optimization problems coincide.

The Difference to the Case of Transaction Costs

The point that explains the difference between our result and that of Chalasani and Jha in [15] is the following. Under no transaction costs and complete markets, there is only one node per path such that the value of the superhedging portfolio fully replicates the derivative’s payoff. This unique node per path would correspond to the optimal exercise of the derivative.

In the setting of [15] , rebalancing the superhedging portfolio is possible at any point in time, and the derivatives have well-defined payoffs at any point in time. However, due to transaction costs, it may be optimal for their problem not to rebalance at some points in time. The cheapest superhedging strategy could then be to replicate the derivative’s payoff in consecutive points in time, for a given path. These points with full replication correspond to optimal stopping. Since there may be more than one per path, the optimal stopping time would be randomized.

In our case it is not possible to exercise the derivative when the underlying asset is not traded, and hence there is no need to hedge for exercise at those points where it is not possible to rebalance the portfolio. In particular, in the case of probabilistic dry markets, our representation of the superreplicating bounds with deterministic stopping times is strongly driven by the fact that we consider the enlarged filtration resulting from the price process and the trade-existence process. This enlarged filtration allows for at most one node, per path, such that the value of the superhedging portfolio fully replicates the derivative’s payoff, avoiding this way the randomized stopping times. If that were not the case, the resulting stopping times could also be randomized. In fact, had we considered only the filtration generated by the price process, for any given price path it could be optimal fully replicate the derivative’s payoff at different moments in time.

3.2. Lower Bound for the Value of an American Derivative

The lower bound for the value of an American derivative (also called its lower hedging price) is the minimum value for which the derivative would be traded without allowing for arbitrage opportunities. Such lower bound coincides with the value of the most expensive self-financed portfolio that the buyer of the American derivative can sell in order to be completely hedged.

For any given stopping time consider any node, such that is a pre- decessor of, with. Let the set of and all its predecessors be denoted by, i.e.,

For any given stopping time consider the portfolio constituted of shares of the underlying asset and an amount invested in the risk free asset, with. Note that if and is an arbitrary successor of, then and, since the portfolio can not be rebalanced at time t. Moreover, for any given two different sets and with common values up to time t, it was assumed that

The value process of the portfolio is given by

For each consider the set of portfolios, one for

each node that is a predecessor of the node where is equal to one. Let it be denoted by, i.e.,

The set of these set of portfolios, one for each be denoted by, i.e.,

For a long position in the derivative, a set of portfolios that belongs to is said to be a self-financed strategy if for any nodes and that are predecessors of the node, such that,

(9)

with, and.

A set of portfolios that belongs to, is said to be a superreplicating strategy if the value of each portfolio is lower than or equal to the payoff of the derivative at any node in the next transaction time. In other words, for any trading dates and such that and and arbitrary nodes, and such that, the portfolio at, , must be such as to generate in a value such that

(10)

For each consider the most expensive portfolio that is self-financing and superreplicating, i.e., the most expensive portfolio that respects conditions (9) and (10), respectively. Let this portfolio be denoted by. The lower bound must satisfy

More formally, the lower bound for the value of the American derivative can thus be seen as the solution of the following problem:

subject to the superreplicating constraint

if. However, if, the superreplication condition is defined for any node such that, and is given by

for any such that and.

Additionally, for any node such that the self-financing conditions apply, i.e.,

for any such that, for any such that with and.

Let us consider the worse scenario in what concerns the existence of trade, that is, the situation that corresponds to the with the highest number of zeros. This situation corresponds to deterministic dryness. Let this be denoted by.

Theorem 7. The lower hedging price of an American derivative in a dry market can be written as

with and for any and

Proof. Notice that the solution of the deterministic case (corresponding to in the general probabilistic case) respects the restrictions of the probabilistic case. We are thus reduced to solve the problem when. As in the case of the upper bound the result follows from the construction of the dual problem.

The lower bound solving the problem above can also be seen as the solution of a more intuitive problem, maximizing the expected discounted payoff, of the derivative over all possible stopping times, when the expectation is minimized among all adjusted probability measures. In other words,

Theorem 8. The lower hedging price of an American derivative in a dry market can be written as

with. Additionally, if there is a probability measure with positive probability on every path, then the lower hedging price of an American derivative in a dry market can be rewritten as

where, as before.

Proof. Follows from the result of the last theorem together with Theorem 2.

This result has already been conjectured as an extension in [17] . When the market is complete then is a singleton and the two bounds coincide with the unique arbitrage free value of the American derivative.

4. Comparison of the Results

In this section we will compare the arbitrage-free bounds of an American derivative in a deterministic dry market (when), in a probabilistic dry market (when) and in a loiquid market (when).

The upper bound in a probabilistic dry market is higher than or equal to the upper bound if the market is dry in the deterministic sense. Moreover, it is also equal to or higher than the upper bound if transactions were possible at all points in time (). The reason is that we are using the pure arbitrage-free concept. If, at a given point in time, it becomes possible to transact with a given probability, the seller of the American derivative must hedge against the possibility of exercise at that point in time. The value of the probability is irrelevant because he will hedge against the worse scenario. In what concerns the upper bound in a deterministic dry market it can be smaller or higher than the upper bound if transactions were possible at all points in time. The reason for this is quite intuitive. Consider an American derivative with a very high payoff in a given moment where transactions were not possible due to the deterministic dryness. If transactions were possible at that given moment in time, the value of the American derivative could increase to become higher than the upper bound in a deterministic dry market. Summing up, , and.

The lower bound in a probabilistic dry market is equal to the lower bound if the market is dry in the deterministic sense. Moreover, it is also lower than or equal to the lower bound if transactions were possible at all points in time (). The reason is as follows. The lower bound is the value of the most expensive portfolio that is self-financed and superreplicates the payoffs of the derivative that is being bought, i.e., at the exercise date its value is smaller than, or equal to, the payoff of the derivative that we are receiving. If a given point is not possible to transact and then becomes possible to transact with a given probability several constraints, which concern the exercise at this additional date, are added to the problem that characterizes the lower bound. Hence,. However, as the solution of the deterministic case is a possible solution of the probabilistic case we conclude that. In what concerns the comparison with the case where transactions are possible at all points in time we have. The reason is that the constraints of the problem that characterizes the lower bound when transactions are possible at all points in time are a subset of those in the probabilistic case.

If the market is incomplete, even with the existence of transactions at all points in time, it is in general not possible to find a unique arbitrage free value for the American derivative. However, it is also possible to establish an arbitrage free range of variation for the value of the American derivative. This range will be a subset of the arbitrage free range of variation for the value of the American derivative in the case of probabilistic dryness, but may not be a subset of the arbitrage free range of variation in the deterministic case.

In this paper we have considered that the only source of market incompleteness would be the non-existence of underlying trade at some points in time. If transactions were possible at all points in time, markets would be complete and there would be a unique arbitrage-free value for any American derivative. We found out that this unique arbitrage-free value for each American derivative belongs to the arbitrage-free range of variation for its value under a probabilistic dry market. However, it may not belong to the arbitrage-free range if a deterministic dry market is considered.

5. Exercise Policy

In order to understand the optimal exercise policy, we start presenting the case of a complete market.

5.1. Complete Markets

In the case of complete markets, the value of an American derivative is given by

(11)

where, as before. If the solution is unique, the stopping time that solves (11) is the optimal exercise policy. Let us analyze this result in some detail. Given an optimal stopping time, we may define a stopping time frontier as follows.

Definition 10. A stopping time frontier is the set of nodes (i, t) such that.

Recalling that there is an optimal stopping node for each possible path5, we define the interior of the stopping time frontier as follows.

Definition 11. The interior of the stopping time frontier is the set of predecessors of the stopping time frontier.

It follows that no rational agent exercises the American derivative at a node inside the stopping time frontier, because at such nodes, the American derivative is worth more than the corresponding exercise. A rational agent would exercise the American derivative whenever the stopping time frontier is reached. This happens because the derivative’s payoff at that point is larger than the cost of a replicating portfolio, guaranteeing the derivative’s payoff in the future.

If the solution is not unique, there may be indeterminacy, even in this case of complete markets. An example illustrates this point. Consider the non-terminal node and two of its immediate successors, and. The replicating portfolio, at node, is the pair. Assume that this portfolio satisfies

(12)

We also assume that, at node,

(13)

Moreover, let and denote the superreplicating portfolios at nodes and, respectively. We also assume that

In this case, the value of the portfolio, at node, that replicates the value of the American derivative in nodes and is the same as the payoff of the American derivative. Let denote the price of the American derivative at node. In this case. Hence, at node the holder of the American derivative will obtain the same payoff by either exercising or selling the derivative. However, when either node or node is reached, the American derivative will be exercised.

Since the replicating portfolio satisfies (12) and (13), the solution of the dual problem is not unique. There are several node probability measures q solving the maximization problem that characterizes the value of the derivative. Let and denote two possible solutions. In that case, and must satisfy

such that for any with

If the maximization problem characterizing the value is not uniquely solved by a node probability measure q, then the stopping time and the adjusted probability measure are also not uniquely defined. For instance, the value can be written as

with, , and

. Actually, the solution can be written with randomized stopping times.

As the stopping time is not unique, there are several stopping time frontiers, each one associated with a different stopping time. For any node inside all possible stopping time frontiers, the argument of the unique case solution applies and the agent does not have any incentive to exercise the American derivative. However, when the first stopping time frontier is reached, namely node, the American derivative may be exercised. At node the value of the replicating portfolio, the payoff of the American derivative and its market value are the same. If the holder of the American derivative wants to guarantee the highest possible payoff at node, the derivative must be either exercised or sold at that node. If the holder of the American derivative wants to guarantee a given payoff at some successor of, there may be an incentive to exercise or sell the American derivative, and to use the proceeds to buy a replicating portfolio providing the same payoff as the American derivative at some successors, and a higher payoff at all other successors.

In the case where several stopping time frontiers coexist in this complete market setting, the exercise at any stopping time frontier before the last frontier provides a payoff equal to the value of the derivative. Also note that the last stopping time frontier is reduced to the role of a unique stopping time frontier, if the American derivative is not exercised at the previous frontiers.

5.2. Incomplete Dry Markets

With incomplete dry markets the problem is more complex. In order to characterize the optimal exercise policy, we use the stopping time that solves the upper bound of the arbitrage free range of variation. Several points must be addressed.

First, if the reduced filtration is considered, the solution may involve randomized stopping times. Although it is not possible to conclude about an optimal exercise policy in this situation, we can still assign probabilities to the exercise of the American derivative at different nodes.

Second, if we consider the enlarged filtration, where ordinary stopping times are enough to describe the upper bound, the stopping time is not uniquely defined for all paths. In order to work out this case, we now extend the definition of a stopping time frontier for the case of incomplete markets as follows.

Definition 12. A stopping time frontier is a pair such that.

Remark 1. Notice that complete markets corresponds to the case where there is only one vector, and the definition above reduces to the first definition of a stopping time frontier.

Remark 2. Note that for two different sets and with common values, up to time t, if then. Therefore.

Just as in the complete markets’ case, the interior of the stopping time frontier is defined as the set of predecessors of the stopping time frontier.

Even for price paths with a strictly positive q, the optimal stopping exercise is not uniquely defined using pure arbitrage arguments. For a given realization of the stochastic process, consider a path of the price process with a strictly positive q, and let be the node such that. Hence, and, if node is reached, the derivative will be exercised. However, it may be exercised at any predecessor of node. Let a predecessor of be denoted by. The reason for the possibility of an American derivative be exercised at is as follows. Using pure arbitrage arguments, it is possible to conclude that at any predecessor of, the price of the derivative is higher, or equal, to its payoff6. If the price is higher than the payoff at, i.e., , any rational agent is better off selling at, rather than exercising, the derivative. If the price of the derivative equals its payoff at,7 i.e.,

(14)

a rational holder who wants to guarantee a given amount at is indifferent between exercising or selling the derivative. In either case, the proceeds would not suffice to buy a superreplicating portfolio that would assure the derivative value at. However, if this agent is concerned with the wealth at a successor of different from, he may use the proceeds to buy a superreplicating portfolio providing the required payoff in that successor of.

However, if the American derivative is not exercised at any predecessor of the stopping time frontier, it will be exercised when the stopping time frontier is reached. The reason is that, at the frontier, the payoff is higher than the value of its replicating portfolio. However, if in a given path there is no node with a strictly positive q, the optimal stopping time can be such that for some node with zero probability measure. As it is possible to have more than one node with zero probability measure, the exercise policy may not be uniquely defined.

A third and final point, is that the situation occurring in the complete market case leading to a non-unique solution of the dual problem, may also happen when markets are incomplete.

5.3. Completeness versus Incompleteness Driven by Dryness

In this section we establish the following result.

Proposition 9. For every path such that the stopping time is unique, the stopping time frontier under complete markets is contained in the union of the stopping time frontier under dry markets and its interior.

Proof. Consider a given, such that. Let be the value, at the node, of the cheapest self-financing portfolio that, from time on, superreplicates all future payoffs of the American derivative. If the node, belongs to the stopping time frontier, then. Define corresponding to in the case of perfectly liquid markets. Both and are the solutions of minimization problems with the same objective function. Since the constraints characterizing are contained in the set of constraints characterizing, it follows that. Therefore, for any given,

.

Hence, nodes in the interior of the stopping time frontier under complete markets are also in the interior of the stopping time frontier under incomplete markets. On the other hand. This means that nodes at the stopping time frontier under incomplete markets are not in the interior of the stopping time frontier under complete markets, completing the proof.

We now turn to the case where there is not a unique stopping time. In that case, for each path w, pick the node such that

.

Let the set denote the envelope of the stopping time frontiers. We now have the following.

Proposition 10. The envelope of the stopping time frontier under complete markets is contained in the union of the envelope of the stopping time frontiers under dry markets and its interior.

Proof. Analogous to the proof above.

We now arrive to a quite significant corollary of this exercise in incomplete dry markets.

Corollary 1. Under uniqueness of the stopping time, rational exercise of American options under incomplete markets driven by dryness may occur later than it would occur under complete markets.

Remark 3. Notice that, under dry markets, American options may be exercised before their optimal stopping time, only under the condition specified by Equation (14), i.e., only under indifference. If not for that case, market incompletenes may only affect optimal exercise of an American option by delaying it.

6. Conclusions

An analysis of the optimal exercise of American options in a context where market’s incompleteness is generated by transaction costs leads to the conclusion that the optimal exercise is characterized by randomized stopping times. Our paper analyzes the same problem when market incompleteness is generated by dry markets, making clear that the need for randomized stopping times depends on the way market incompleteness is generated. We conclude that in the case of deterministic dry markets, the bounds for the values of American derivatives are the supremum of the implied European derivatives (i.e., European derivatives with the same underlying traded in the same dry market), this supremum being taken over deterministic stopping times. In the general probabilistic dry markets’ case, there is an additional source of uncertainty, namely the existence or not of trade at given points in time, which can be interpreted as the realization of an additional stochastic process. If an enlarged filtration, resulting from the price process and the trade existence process is considered, only ordinary stopping times are required to describe the upper and lower bounds. However, if the enlarged filtration was not considered, and the stopping times were defined by using only the filtration induced by the price process, then they could be randomized. This last conclusion recovers the results for the transaction cost model.

In a complete market the arbitrage free value of the derivative is unique and equal to the value of the replicating portfolio. However, in our incomplete market framework driven by dry markets, that fact no longer holds true. Ruling out arbitrage opportunities identifies a range of variation for the value of the derivative. The arbitrage-free value intervals for the deterministic case, for the probabilistic case and for the liquid case are compared. We find out that the range in the probabilistic case includes the range of the deterministic case and also the unique value of the liquid case. Moreover, the lower bound in the probabilistic case coincides with the one in the deterministic case. However, a relation cannot be established between the arbitrage-free range in the deterministic case and the one in the liquid case when transactions are possible at all points in time.

Moreover, when a complete market is considered, the optimal exercise policy corresponds to the stopping time that is the supremum of the implied European derivatives. Consistently with the absence of a unique arbitrage-free price, if American options are considered in this dry markets setting, the optimal exercise policy is also not well defined. The reason is that there are paths where the stopping time is not uniquely defined and in addition, the fact that if the filtration induced by the price process is considered, randomized stopping time must be used. However, we were able to show that incompleteness generated by dry markets may in general delay the optimal exercise of American derivatives.

Acknowledgments

This work was funded by National Funds through FCT―Fundação para a Ciência e Tecnologia under the project Ref. UID/ECO/00124/2013 and by POR Lisboa under the project LISBOA-01-0145-FEDER-007722. This support is greatly appreciated.

Cite this paper

de Matos, J.M. and Lacerda, A. (2016) Randomized Stopping Times and Early Exercise for American Derivatives in Dry Markets. Journal of Mathematical Finance, 6, 842-865. http://dx.doi.org/10.4236/jmf.2016.65057

References

Appendix

Proof of Theorem 3

Proof. The proof that is an adjusted probability measure is straightforward. In what concerns the randomized stopping time, X, we must check that and that condition (2) is satisfied.

For any given node such we have

Consider a given path such that at the terminal node we have. In that case

Consider a given path such that at the node we have and. In that case

(15)

Let be a successor of. If then.

Moreover, as then. As a result, Equation (15) can be written as

However, if there are not a successor of such that then

(16)

(17)

can take two possible values: 0 and. The situation is the same as the one just described. In the case, as

then. Moreover,

. For any such that then. For a given such that and with

then. As a result, Equation (16) is verified

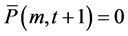
and the proof is complete.

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

Or contact jmf@scirp.org

NOTES

¹See, among others, [2] - [9] .

²For a discussion of this point see, among others, [16] , p. 37.

³A self-financed portfolio is a portfolio that generates enough wealth to rebalance the portfolio according to any future state of nature.

⁴A replicating portfolio is a sequence of portfolios such that the value of each of them is larger than or equal to the payoff of the derivative at any non-terminal node in the next transaction time.

⁵If the solution is unique, there is a unique strictly positive q associated to each path. Hence, the stopping time is uniquely defined.

⁶The reason is that and. Hence, the arbitrage-free price must be higher than the payoff, i.e.,.

⁷In this case we should have