Received 8 April 2015; accepted 17 May 2015; published 22 May 2015

ABSTRACT

Predicting stock price movement is generally accepted to be challenging such that until today it is continuously being attempted. This paper attempts to address the problem of stock price movement using continuous time models. Specifically, the paper provides comparative analysis of continuous time models―General Brownian Motion (GBM) and Variance Gamma (VG) in predicting the direction and accurate stock price levels using Monte Carlo methods―Quasi Monte Carlo (QMC) and Least Squares Monte Carlo (LSMC). The hit ratio and mean-absolute percentage error (MAPE) were used to evaluate the models. The empirical tests suggest that either the GBM model or VG model in any Monte Carlo method can be used to predict the direction of stock price movement. In terms of predicting the stock price values, the empirical findings suggest that the GBM model performs well in the QMC method and the VG model performs well in the LSMC method.

Keywords:

Monte Carlo, Stock Price, Geometric Brownian Motion, Variance Gamma, Maximum Likelihood Estimation, MAPE, Hit Ratio

1. Introduction

In this paper we deal with the problem of prediction of stock price movement (increase or decrease) that has been there over years. Several methods have been proposed and have predicted stock price movement with variable degrees of accuracy such that until today, prediction of stock price movement is continuously being attempted. A manifold of factors such as economical, political, social and psychological factors interact in a complex way influencing stock price movement. It is no doubt that prediction of stock price movement is quite challenging. This paper is an attempt to predict stock price movement using continuous time models. We believe that continuous models are suitable to capture the unpredictable dynamics of stock prices to a certain extent.

The models for prediction of stock price movement have several uses to researchers and practitioners alike which include optimal portfolio construction and executing best informed buy/sell orders. Also, a major boost for the models of stock price movement is in derivatives models to determine fair values of derivatives and simulation models for risk management purposes.

Most studies have focused on the accurate estimation of the value of stock price. In most cases, the accuracy of the estimations is measured by the error between the estimates and observed values. However, different investors use diverse trading strategies and strategies based on minimizing the error between observed values and the estimates may not appeal to them [1] . Some recent studies have illustrated that forecasts from trading strategies based on the direction of stock price change may be more effective and can generate higher returns. Thus, trading strategies based on predictability of direction of stock need attention in the effective development of market trading strategies.

In the literature, there exist a vast number of articles addressing the accurate estimation of the value of stock price. However, to the best of our knowledge, there are few studies which look at the predictability of the direction of stock price. In this respect, we cite studies by [2] , who explores the relationship between the direction of interday and intraday price changes on the S&P 500 futures. [3] investigated on the predictability of the direction of change in the future spot exchange. [4] concluded that the performance of cross-hedging improves if the direction of changes in exchange rates can be predicted. [1] provided a comparative evaluation of the forecasting performance of a group of classification models to that of a group of level estimation models. The classification models were used to forecast the direction of index returns and the level estimation models were used to estimate the value of the return. Recently, [5] attempted to predict the direction of stock price movement with focus on emerging markets using data mining techniques.

We follow the approach of [1] in this work. Instead of making a comparison between classification models, which predict direction based on probability, and level estimation models, which forecast the accurate price level, we resort to using continuous time models in Monte Carlo framework to achieve both objectives of predicting the direction of stock price and accurate stock price level. The major contributions of this work are comparative analysis of continuous time models to predict the direction and accurate price levels of stocks in the Monte Carlo framework.

[6] and [7] used the Geometric Brownian Motion (GBM) model to forecast share prices for short-term investments. Though the GBM model is good for forecasting share price movements, there is ongoing active research to improve upon it substantially. In the past decades, there have been several theoretical and empirical studies that have tried to address this issue. Amongst these studies, the most important are studies by [8] [9] and [10] . Of the proposed models from the studies, we consider the model proposed by [10] in this work. [10] proposed a stochastic process for stock price movement called the Variance Gamma (VG) model. The empirical findings of the authors claim that the VG model is a good contender for forecasting share price movements. Hence, the interest to this work is the comparative analysis of continuous time models―GBM model and VG model in stock price movement.

The assumptions on which the continuous models are based meet the rules imposed by the weak Efficient Market Hypothesis. The weak Efficient Market Hypothesis guarantees transparency in the sense that it gives everyone the same information about a stock. According to the hypothesis, the only relevant information about a stock is the current value, so as to be able to determine future stock price movement.

The rest of the paper is organized as follows: the Monte Carlo techniques used for simulating stock price processes are discussed in the next section. In Section 3 we discuss the dynamics and parameter estimation of the models used in this work. Then we discuss the design of the experiments in Section 4. In this section we also provide results of the performance of the models. Section 5 formulates our conclusions and carries summary of our findings.

2. Monte Carlo Methods

We look at the techniques for simulating the stock price processes encountered in this work. The Monte Carlo methods lend themselves naturally to this task as they are useful in estimating numerically the values of integral expressions especially in high dimensions. The simulation procedures used in here are found in [11] .

2.1. Crude Monte Carlo Method

The integral of a Lebesgueintegrable function can be expressed as the expectation of a function f evaluated at a random point. Consider an integral on the unit cube 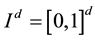in d dimension. Let x be the uniformly distributed random variable on the interval. Then:

(1)

The Monte Carlo quadrature formula is based on the probabilistic interpretation of the integral. Now, consider a sequence which is sampled from the uniform distribution. An empirical approximation to the expectation then is:

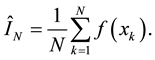(2)

According to the Strong Law of Large Numbers, the approximation converges to the true value of the integral:

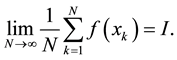(3)

This means that with probability 1 as. 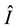is therefore an unbiased estimator for I (see [12] ).

Now in crude form, Monte Carlo simulations are computationally inefficient. A large number of simulations are generally required so as to achieve high degree of accuracy. However, the efficiency can be improved by either using other methods such as variance reduction method, quasi-Monte Carlo method or least-squaresregres- sion Monte Carlo method [13] . Of these methods, quasi-Monte Carlo and least-squares regression Monte Carlo methods are of interest to our work.

2.2. Quasi-Monte Carlo Method

Quasi-Monte Carlo (QMC) method, also called low-discrepancy, can be described in simple terms as the deterministic method of the crude Monte Carlo method. The random samples in the Monte Carlo method are instead replaced by well-chosen deterministic points. Quasi-Monte Carlo thus makes no attempt to mimic randomness. It rather generates sample points that are literally too evenly distributed to be random and thus selectively tries to increase accuracy [11] .

Suppose for the unit cube integration domain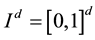, we have the quasi-Monte Carlo approximation:

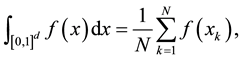(4)

which formally looks like the crude Monte Carlo estimate but is now used with the deterministic points. These points are chosen judiciously so as to guarantee a small error.

It is intuitively clear that:

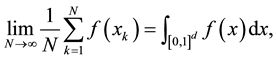(5)

and that the points x_k are chosen so as to fill the hyper-cube uniformly, and achieve a maximal degree of uniformity and a low degree of discrepancy. The discrepancy is a measure of the “level of uniformity” or more exactly the deviation from uniformity. It is defined as:

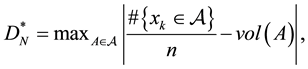(6)

where 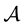is a collection of subsets of, is the number of points contained in and is volume (measure) of. If we choose to be the collection of all rectangles in of the form:

(7)

we define the star discrepancy. The lower the star discrepancy, the more uniformly distributed the points are. There exist different kinds of pseudo-random sequences.

In this work, we use Halton sequences. Halton sequences are generally d-dimensional sequences with values in the unit hypercube. The first dimension of the Halton sequence is the van der Corput sequence base 2, the second dimension is the van der Corput sequence using base 3, the third dimension is the van der Corput using base 5, and so on. Dimension d of the Halton sequence is the van der Corput sequence using the d^th prime numbers as the base.

2.3. Least Squares Regression Monte Carlo Method

Consider a reward function that depends on both and time t such that:

(8)

where r is the discount factor. Suppose is a stochastic process defined on a probability space. For any point in time n and a given stopping time with, we define the value process by:

(9)

where we let and the optimal value process V is defined by:

(10)

where signifies the optimal stopping time.

This is a typical optimal stopping problem whereby an investor has to decide the right time or optimal time to sell a stock in order to maximize the expected reward. In particular, we are interested in the optimal expected reward at an optimal stopping time. The findings from a study by [14] and further supported in [15] suggest that over a finite horizon, a selling strategy is optimal at the terminal time T or at the moment when the stock price hits the maximum price. In our context, we are interested in the optimal strategy at the terminal time T.

To tackle this stochastic control problem, we use Dynamic Programming. The main idea originated from [16] ’s principle which states that: An optimal policy has the property that whatever the initial state and initial decisions are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision. Thus, the optimal value process V is the solution of the following backward recursion:

(11)

(12)

It is optimal to stop at time n if and only if. If stopping at n is not optimal, then and. The region where, that is, the region where it is optimal to terminate the process and receive the reward is called the “exercise region” and the compliment to this region is called the “continuation region”.

To continue with calculations, we need to estimate the conditional expectation term, that is, the continuation value at each time step. The most popular approach to estimate the continuation values is the Least Squares regression-based Monte Carlo (LSMC) method suggested by [17] . The main idea of the Least Squares Regression is to approximate the conditional expectation with linear combination of a set of R basis functions, at each time step. Denote in this setup. Now, for each time step, we assume the following multi-linear model:

(13)

We generate N independent sample paths of the process X, denoted by, for. The squared residual along path k is:

(14)

Ordinary Least Squares (OLS) regression is performed to find the parameter vector that minimizes the sum of all squared residuals:

(15)

Once we have determined the vector, the continuation value at time along path is estimated by the fitted value of regression:

(16)

For the basis regression functions, we choose the weighted Laguerre polynomials suggested by [11] , which are defined as:

(17)

where is the Laguerre polynomial defined as:

(18)

3. Simulation of Stock Price Processes

In this section, we discuss the dynamics of the models used in this work. The price of a particular stock at a future time t is usually unknown at the present time. Thus, we think of the stock price as a random variable. The stock price process is denoted by, where is the price at time. The following is a brief overview of the dynamics used in simulating the stock price process.

3.1. Dynamics of Geometric Brownian Motion Process

The Geometric Brownian Motion (GBM) stock price dynamics under the risk neutral measure are given by:

(19)

where r is the risk-free rate and is the volatility parameter. Applying the Itóformula to the log-returns yields:

(20)

Integrating the above stochastic differential equation over the time interval, where, gives:

(21)

This gives us the recursive expression for:

(22)

Assuming an equidistant grid, let, for all i. Let, for . Notice that, so we can replace by where are independent standard normal random variables for all. The discretized form becomes:

(23)

3.2. Variance Gamma Process

Variance Gamma (VG) process falls under the class of infinite activity pure jump models. In the pure jump models, one does not have to introduce a diffusion component since the dynamics of jumps already are rich enough to generate non-trivial small time behavior. However, models of this type can be constructed by Brownian subordination. Subordinating Brownian motion with drift by the (subordinator) process S, we obtain a new Lévy process.

The subordinating process under the Variance Gamma model is the Gamma process. The Gamma process, like the Poisson process, is a pure jump process with no diffusion component. Jumps of negligible size arrive infinitely often in the Variance Gamma model and the infinite activity allows the model to behave like a diffusion process for small jumps. Jumps of non-negligible size occur with a finite frequency and the arrival rate of these jumps decrease monotonically with the jump size.

So, the Variance Gamma process uses a Gamma process to time change a Brownian motion. Instead of evaluating a Brownian motion at time t, rather it is evaluated at time, where follows a gamma process with and. [18] define a Variance Gamma process, , as a time changed Brownian motion as follows:

(24)

The dynamics of the stock price under the risk-neutral measure are:

(25)

where, are stock prices at times t and 0, respectively, r is the risk-free rate of return of the stock and is a compensator term chosen to make sure that the Variance Gamma process is a martingale.

We can write the dynamics in Equation (25) as:

(26)

Consider the dynamics over the time interval, where. As above, assume an equidis- tant grid so that, for all. Also, let and. Since the Gamma process is used to subordinate the Weiner process, the discretized Variance Gamma process becomes:

(27)

3.3. Parameter Estimation

The parameters of the General Brownian model (with parameter) and Variance-Gamma model (with parameters) were estimated using the maximum likelihood estimation (MLE) method. The maximum likelihood method postulates that the most sensible values of the parameters are those that maximize the likelihood of the observations. The likelihood function of the sample data is given by:

(28)

where is the parameter set and is the probability distribution function (pdf) of the proposed distribution. A value of that maximizes is known as the maximum likelihood estimate (MLE), that is, is a MLE of if:

(29)

It is often simpler to maximize the log-likelihood function:

(30)

[19] suggested a method, which is used in this work, to approximate more efficiently the likelihood function using the fast Fourier Transform. For a given parameter vector, the density function is calculated at N points (where) over a finite range by inverting the characteristic function with the use of fast Fourier Transform. Given m observed data points, [13] arranged the observed data for into their corresponding intervals for and counted the number of observed data points that fell into each interval. The intervals for the bins are formed using the density evaluated at some pre-specified points. The likelihood of observing this binned data is then maximized by appropriate choice of the parameter vector.

However, solving the likelihood equations is often non-trivial. We had to rely on global optimization algorithms to obtain the maximum likelihood estimates. It should be hinted that the solutions yielded by these algorithms were sensitive to the choice of initial values because the log-likelihood function may have several local minimas.

4. Data and Experimental Results

4.1. Data Description

We selected 19 stocks from the ALSI40 (JSE Top 40 Index) for the purpose of this work, which are representative of the different industry sector categories. The share code, share name and industry sector categories are given in Table 1. The data employed in this paper comprise the returns, open prices, close prices and midprices. The data were sampled every 5 minutes from 0900 hrs until 1700 hrs CAT. One of the indisputable stylized features of financial time series is that they exhibit periodicities, or recurring patterns. We examined returns for the ALSI40 (JSE Top 40 Index) stocks at 5 minute intervals and found out that significant returns were on average earned during the first 30 minutes of trading.

Continuous time models provide better predictions when used to model stock prices over longer periods of time rather than short periods of time. As a result, we try to predict the stock price movement on a weekly basis.

The predictions were made at the start of the first business day of the week.

The models were tested for their prediction capabilities when the market was generally trending downwards as well as when the market was generally trending upwards. For the former, the sample data set runs from May 2008 to April 2009, and for the latter, the sample data set runs from September 2010 to August 2011. Both sample data sets span for a period of approximately a year each. About two thirds of the observations were used for In-Sample predictions and the remainder of the observations were used for one-step ahead forecast, which we consider as our out-of-sample prediction forecast. The statistical tests were performed at 5% significance level. The results reported here are for 2-tailed tests.

4.2. Performance Evaluation of the Models

Now, we evaluate the performance of the models discussed in the previous sections. From the numerous choices of performance evaluation metrics, we choose to use the mean-absolute percentage error (MAPE) and hit ratio to evaluate the performance of the models. The mean-absolute percentage error (MAPE) measures the magnitude of error from the observed prices in percentage terms. The formula for calculating MAPE is:

(31)

where is the i^th actual observation (price) and is the predicted observation (price).

The hit ratio is simply the accuracy of the predicting model measured in percentage over number of predictions. It is determined by the number of correct signs (correct price direction) divided by the total number of predictions. The hit ratio is given as:

(32)

For each performance evaluation metric, we make a comparative analysis of the models―GBM or VG, under each simulation method―QMC or LSMC. Furthermore for each performance evaluation metric, we make a comparative analysis of the simulation models―QMC and LSMC, for each type model―GBM or VG. The following are the findings of the evaluations for the two different time periods selected.

4.2.1. Performance Evaluation―Downward Trend Analysis

Table 2 shows the average hit ratios of the stocks from the sample obtained using the quasi-Monte Carlo method. The In-Sample average hit ratio for the GBM model is 55.41%, whereas for the VG model is 55.71%. For

the Out-Sample, the average hit ratio for the GBM model is 51.64% and the VG model is 51.97%. The All Periods average hit ratios for the GBM model and VG model are 54.25% and 54.55%, respectively. The statistical t-tests showed no significant differences in the hit ratios from using either of the models for all the different testing periods (In-Sample, Out-Sample, All Periods).

Table 3 shows the average hit ratios for the stocks from the sample acquired using the Least Squares Regression Monte Carlo Method. The average hit ratios for the different testing periods (In-Sample, Out-Sample, All Periods) are within a range of 49% - 52%. The statistical t-tests showed no significant difference from using either the GBM model or VG model for all the different testing periods.

In addition, to assess which simulation method is better for hit ratios we made a comparative analysis of each type of model (GBM model or VG model) under each type of simulation method. Table 4 gives a comparison of the GBM model hit ratios under the different simulation methods.

Table 5 shows the performance of the VG model under different simulation procedures. The t-tests for results in Table 4 and Table 5 show no significant differences from using either simulation method when using either the GBM model or VG model in predicting the hit ratios.

Next, we give a comparative analysis for the downward trend using the MAPE as the performance measure. Table 6 reports the average MAPEs of the models obtained using the quasi-Monte Carlo method.

Under the quasi-Monte Carlo method, the MAPEs for the VG model is greater than those of the GBM model for all the different testing periods. The statistical tests confirm no significant differences between the two models in predicting stock price values.

Table 7 reports the MAPEs of the models using the Least Squares Regression Monte Carlo method. From using the Least Squares Regression Monte Carlo method, the MAPEs are lower for VG model as compared to the GBM model for all the different time periods. The t-tests showed that there are significant differences when using either the GBM model or VG model in predicting the stock price values.

Again, we test to assess which simulation method is better at predicting stock price values. Table 8 gives a comparison of the GBM model under the different simulation methods. The mean MAPEs for the GBM model under quasi-Monte Carlo method are lower than the mean MAPEs under the Least Squares Regression Monte Carlo method. The statistical tests showed significant differences between the simulation methods in predicting stock price values when using the GBM model.

Table 9 gives the performance of the VG model under the different simulation methods. The mean MAPEs are lower under the Least Squares Regression Monte Carlo method as compared to the quasi-Monte Carlo Method for all different time periods. The statistical tests confirm the significant differences between the simulations methods in predicting stock price values when using the VG model.

4.2.2. Performance Evaluation―Upward Trend Analysis

Table 10 shows the average hit ratios of the stocks from the sample for different time periods obtained using the quasi-Monte Carlo method. The average mean hit ratios were within a range of 46% - 49%. The results from the statistical tests indicate no significant differences in the hit-ratios from either using any of the models for the different test periods.

Table 11 shows the average hit ratios of the stocks obtained using the Least Squares Regression Monte Carlo method. The average hit ratios for the GBM model are greater than those of the VG model in the In-Sample period as well as for All Periods combined. There are statistical differences from using the models in predicting the hit ratios for the In-Sample period. However, the average hit ratio for the VG model exceeds that of the GBM model in an Out-Sample. We fail to find any significant difference between the models in the Out-Sample and All Periods combined.

Table 12 gives a comparison of the GBM model average hit ratios under the different simulation methods. The results in Table 12 show that the GBM model has high hit ratios under the Least Squares Regression Monte Carlo method as compared to the quasi-Monte Carlo method. We find significant differences between the simulation methods in the In-Sample and for All Periods combined. However, there is no significant difference for the Out-Sample.

Table 13 shows a comparison of the VG model average hit ratios under the different simulation methods. The average hit ratios increase as we move from the quasi-Monte Carlo method to the Least Squares Regression

Monte Carlo method for the Out-Sample and All Periods combined, except for the In-Sample. We find statistical difference between the simulation methods only for the Out-Sample period.

We move on to give analysis of the models and simulation methods using MAPE. In Table 14 we report the average MAPEs obtained using the quasi-Monte Carlo method. The average MAPEs for the GBM model are less than those of the VG model for all different time periods. We find significant statistical differences from the t-tests in predicting the hit ratios for all the different time periods.

In Table 15 we report the average MAPEs for the models obtained using the Least Squares Regression Monte Carlo method. There are significant reductions in the average MAPEs as we move from using the GBM model to using the VG model under the Least Squares Regression Monte Carlo method for all different time periods. This is further supported by the statistical t-tests which showed significant differences between the models in predicting the stock prices.

Next, we give a comparative analysis of the simulation methods in estimating the stock prices. Table 16 gives a comparison of the GBM model average MAPEs under the different simulation methods. The quasi-Monte Carlo method has lower MAPEs in comparison to the Least Squares Regression Monte Carlo method for all the different time periods. The t-tests showed significant differences between the simulation methods.

Table 17 gives the results of the performance of the VG model under the different simulation methods. The margin of error (MAPE) in predicting stock prices using the VG model reduces drastically when moving from the quasi-Monte Carlo method to the Least Squares Regression Monte Carlo method. The statistical t-tests show that there are significant differences between the simulation methods.

5. Conclusions

This paper addressed the problem of stock price movement using continuous time models. Specifically, the paper provides comparative analysis of continuous time models―GBM and VG in predicting the direction and accurate price levels of stocks using Monte Carlo methods―QMC and LSMC. The performance evaluation metrics used in this paper were hit ratio and MAPE. The t-test was used to show significance. For each performance evaluation metric, we made a comparative analysis of the models―GBM and VG under each simulation method―QMC or LSMC. Furthermore, we made a comparative analysis of the simulation models―QMC or LSMC for each model―GBM or VG. The models were tested for their prediction capabilities when the market was generally trending downwards as well as when the market was generally trending upwards.

For the downtrend analysis, we found no significant difference between the GBM model and VG model in terms of the hit ratio (number of times the predicted direction is correct). We also found no significant difference between the Monte Carlo methods―QMC and LSMC in terms of hit ratios for the downward trend period.

In terms of the MAPEs for the downward trend, there were no significant differences between GBM model and VG model under the QMC method. However, there were significant differences between the GBM model and VG model under the LSMC method. The VG model performs better than the GBM model under the LSMC method in predicting stock price values.

The Monte Carlo methods assessment for the downtrend showed significant differences either using the GBM model or VG model as shown by the MAPEs. The findings hint that the GBM model works well when used in the QMC method whereas the VG model works well when used in the LSMC method.

For the uptrend analysis, we found no significant difference between the GBM model and VG model under the QMC method in terms of the hit ratios. Under the LSMC method there were no significant differences between the GBM model and VG model except for the In-Sample period. In this case the GBM model predicted the direction correctly most of the times in comparison to the VG model.

In the comparison of the Monte Carlo methods, there were significant differences for the GBM model In-Sample and All Periods when used in the Monte Carlo methods. The GBM model predicted the hit ratios most of the times in the LSMC method in comparison to the QMC method. Comparison of the VG model in the Monte Carlo methods showed significant difference for the Out-Sample only with the VG model fairing well in the LSMC method as compared to the QMC method.

In terms of the MAPEs for the uptrend, we found significant differences between the GBM model and VG model. The GBM model fairs better under the QMC method whereas the VG model fairs well under the LSMC method in predicting the stock price values. The findings also show significant differences between the Monte Carlo methods in predicting the stock price values. Again the GBM model performs better in the QMC method and the VG model performs better in the LSMC method.

We summarize the findings as follows: for predicting the direction of stock price (as indicated by the hit ratios), the GBM model or VG model can be used in any Monte Carlo method as most of the times we found no significant differences as evidenced from the t-tests. The hit ratios we obtained are “near” random walk behavior. This hints on how challenging it is in predicting stock price movement. Since the results of the hit ratios are at the same level where even a random predictor can produce them, then our results are justifiable.

For predicting the stock price values (as indicated by the MAPEs), the GBM model performs well under the QMC method and the VG model performs well under the LSMC method. The finding has important implications in risk management simulations.

Acknowledgements

The authors would like to acknowledge support of this work from DAAD, the German Academic Exchange Service, in association with AIMS (African Institute for Mathematical Sciences) and Centre for Business Mathematics and Informatics. The work was done while Hopolang Mashele was a visiting researcher at AIMS.

References

NOTES

^*Corresponding author.