Open Journal of Statistics
Vol.06 No.05(2016), Article ID:71405,7 pages
10.4236/ojs.2016.65069
Asymptotic Efficiency of the Maximum Likelihood Estimator for the Box-Cox Transformation Model with Heteroscedastic Disturbances
Kazumitsu Nawata
Graduate School of Engineering, University of Tokyo, Tokyo, Japan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 18, 2016; Accepted: October 18, 2016; Published: October 21, 2016
ABSTRACT
This paper considers the asymptotic efficiency of the maximum likelihood estimator (MLE) for the Box-Cox transformation model with heteroscedastic disturbances. The MLE under the normality assumption (BC MLE) is a consistent and asymptotically efficient estimator if the “small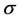 ” condition is satisfied and the number of parameters is finite. However, the BC MLE cannot be asymptotically efficient and its rate of convergence is slower than ordinal order
” condition is satisfied and the number of parameters is finite. However, the BC MLE cannot be asymptotically efficient and its rate of convergence is slower than ordinal order 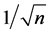 when the number of parameters goes to infinity. Anew consistent estimator of order
when the number of parameters goes to infinity. Anew consistent estimator of order 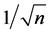 is proposed. One important implication of this study is that estimation methods should be carefully chosen when the model contains many parameters in actual empirical studies.
is proposed. One important implication of this study is that estimation methods should be carefully chosen when the model contains many parameters in actual empirical studies.
Keywords:
Maximum Likelihood Estimator (MLE), Asymptotic Efficiency, Box-Cox Transformation Model, Heteroscedasticity

1. Introduction
The Box-Cox transformation model (BC model) [1] is widely used in empirical studies. For details on this model, see Hossain [2] and Sakia [3] . The maximum likelihood estimator (MLE), which maximizes the likelihood function under the normality assumption (BC MLE), can be asymptotically efficient if the “small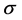 ” condition described by Bickel and Doksum [4] is satisfied. On the other hand, the model with heteroscedastic disturbances, in which variances are different among groups, is also widely used in the analysis of various datasets such as panel data [5] . It is sometimes necessary to consider a model combining these two models. Nawata and Kawabuchi [6] - [11] analyzed length of stay (LOS) in Japanese hospitals using the BC model. They found that the variances among hospitals were often very different among hospitals even after the transformation. Their studies are these cases.
” condition described by Bickel and Doksum [4] is satisfied. On the other hand, the model with heteroscedastic disturbances, in which variances are different among groups, is also widely used in the analysis of various datasets such as panel data [5] . It is sometimes necessary to consider a model combining these two models. Nawata and Kawabuchi [6] - [11] analyzed length of stay (LOS) in Japanese hospitals using the BC model. They found that the variances among hospitals were often very different among hospitals even after the transformation. Their studies are these cases.
It is well known that the MLE is usually an asymptotically efficient estimator when the number of parameters is finite. However, this may not be true when the number of parameters goes to infinity. It is often necessary for us to consider cases in which numbers of groups go to infinity. For example, the new medical payment system known as the Diagnostic Procedure Combination/Per Diem Payment System (DPC/PDPS) was introduced in 2003 in Japan, and as of April 2014, 1863 hospitals had either already joined or were preparing to join; this number has been increasing [12] . The hospitals joining the DPC/PDPS are required to computerize their medical information. This means that it has become possible to analyze a large scale dataset that contains information from many hospitals. In other words, it is necessary for us to consider the asymptotic properties of estimators when the number of groups (hospitals) goes to infinity.
This paper considers the estimation of the Box-Cox transformation model with heteroscedastic disturbances when the number of groups that increases to infinity. In such cases, the conventional maximum likelihood method yields only an estimator whose rate of convergence is slower than ordinal order of  even if the “small
even if the “small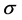 ” condition is satisfied in all groups. Then a new estimation method that can handle these problems is proposed.
” condition is satisfied in all groups. Then a new estimation method that can handle these problems is proposed.
2. BC Model with Heteroscedastic Disturbances
Suppose that 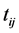 is the explanatory variable of observation j in group i (for example, LOS of patient j in hospital i in Nawata and Kawabuchi [6] - [11] ). I consider the BC model:
is the explanatory variable of observation j in group i (for example, LOS of patient j in hospital i in Nawata and Kawabuchi [6] - [11] ). I consider the BC model:
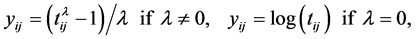 (1)
(1)
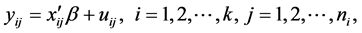
with heteroscedastic disturbances and variances given by
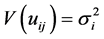 , (2)
, (2)

1If the “small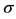 ” condition is not satisfied, we can use the estimator proposed by Nawata [15] instead of the BC MLE. Even in this case, however, we reach the same conclusion as that presented here; that is, a model that considers heteroscedasticity and a number of parameters that goes to infinity is simply a consistent estimator of order
” condition is not satisfied, we can use the estimator proposed by Nawata [15] instead of the BC MLE. Even in this case, however, we reach the same conclusion as that presented here; that is, a model that considers heteroscedasticity and a number of parameters that goes to infinity is simply a consistent estimator of order 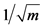 and there exists a consistent estimator of order
and there exists a consistent estimator of order  by a modification of the homoscedastic case.
by a modification of the homoscedastic case.
where 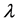 is the transformation parameter,
is the transformation parameter, 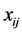 and
and 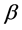 are the vectors of the explanatory variables and coefficients, k is the number of groups, and
are the vectors of the explanatory variables and coefficients, k is the number of groups, and 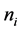 is the number of people in group i. We assume that the “small
is the number of people in group i. We assume that the “small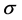

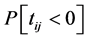
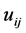
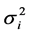
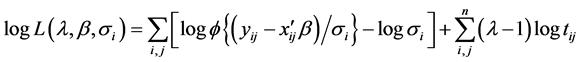
where 

3. Estimation of the Model When the Number of Groups Goes to Infinity
Let the numbers of observations be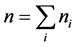
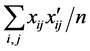

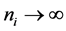
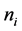
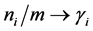
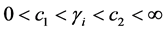



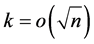
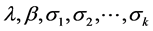
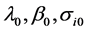
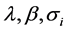
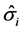

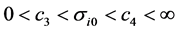
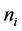

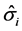
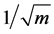


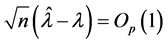
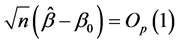
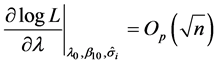

As before, although the values of derivatives are at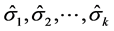
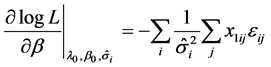
Here,
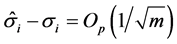
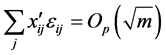
We get
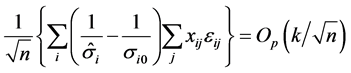
Therefore, if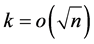
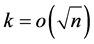
However, for the transformation parameter
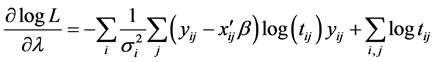
we get [15] [16]

under the “small
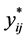
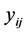
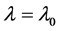
Since
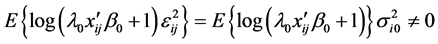
we get

and (4) is not satisfied. This means that the MLE becomes a consistent estimator only of order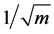

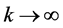

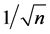

Therefore, 
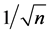
4. A Consistent Estimator of Order
Here, an alternative estimator is proposed by an essential modification of the likelihood function. Suppose that disturbances are homoscedastic and that 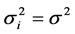
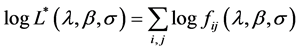
where
Instead of maximizing (15), we considered the roots of the equations,
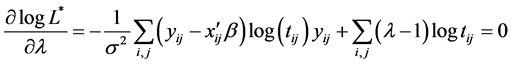
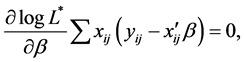
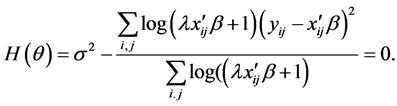
For the standard maximum likelihood method, the variance is estimated by the simple average. However, in this case, the variance is estimated by the weighted average of least squares residuals.
We assume
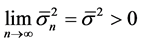
where
Here,
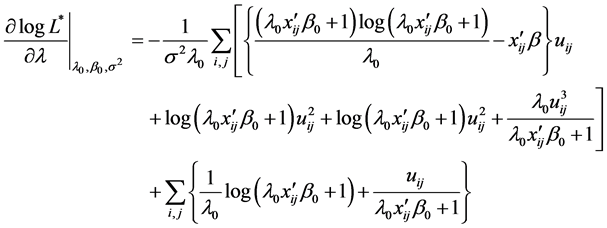
where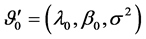
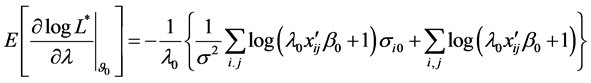
From (21), we get
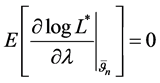
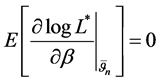

where
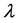
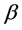
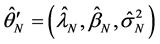


where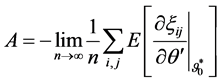
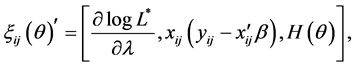
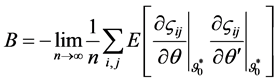





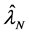

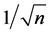
5. Conclusion
This paper considers the estimation of the BC model with heteroscedastic disturbances; that is, variances are different by groups. The BC MLE is a consistent and asymptotically efficient estimator if the “small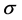

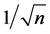
Acknowledgements
The author would like to thank two anonymous referees for their helpful comments and suggestions.
Cite this paper
Nawata, K. (2016) Asymptotic Efficiency of the Maximum Likelihood Estimator for the Box-Cox Transformation Model with Heteroscedastic Disturbances. Open Journal of Statistics, 6, 835-841. http://dx.doi.org/10.4236/ojs.2016.65069
References
- 1. Box, G.E.P. and Cox, D.R. (1964) An Analysis of Transformation. Journal of the Royal Statistical Society B, 26, 211-252.
- 2. Hossain, M.Z. (2011) The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses. Journal of Emerging Trends in Economics and Management Sciences, 2, 32-39.
- 3. Sakia, R.M. (1992) The Box-Cox Transformation Technique: A Review. The Statistician, 41, 169-178.
http://dx.doi.org/10.2307/2348250 - 4. Bickel, P.J. and Doksum, K.A. (1981) An Analysis of Transformations Revisited. Journal of American Statistical Association, 76, 296-311.
http://dx.doi.org/10.1080/01621459.1981.10477649 - 5. Baltagi, B.H. and Griffin, J.M. (1988) A Generalized Error Component Model with Heteroscedastic Disturbances. International Economic Review, 29, 745-753.
http://dx.doi.org/10.2307/2526831 - 6. Nawata, K. and Kawabuchi, K. (2015) Evaluation of Length of Hospital Stay Joining Educational Programs for Type 2 Diabetes Mellitus Patients: Can We Control Medical Costs in Japan? Health, 7, 256-269.
http://dx.doi.org/10.4236/health.2015.72030 - 7. Nawata. K. and Kawabuchi, K. (2015) Financial Sustainability of the Japanese Medical Payment System: Analysis of the Japanese Medical Expenditure for Educational Hospitalization of Patients with Type 2 Diabetes. Health, 7, 1007-1021.
http://dx.doi.org/10.4236/health.2015.78118 - 8. Nawata, K. and Kawabuchi, K. (2015) An Econometric Analysis of Hospital Length of Stay for Cataract Operations in Japan by the Box-Cox Transformation Model and Hausman Tests: Evaluation of the 2010 Revision of the Medical Payment System. Open Journal of Applied Science, 5, 559-570.
http://dx.doi.org/10.4236/ojapps.2015.59054 - 9. Nawata, K. and K. Kawabuchi (2016) Comparison of the Length of Stay and Medical Expenditures among Japanese Hospitals for Type 2 diabetes Treatments: The Box-Cox Transformation Model under Heteroscedasticity. Health, 8, 49-63.
http://dx.doi.org/10.4236/health.2016.81007 - 10. Nawata, K. and Kawabuchi, K. (2016) Did the Revision of the Japanese Medical Payment System Work Properly?—An Analysis of Averages and Variances of Length of Hospital Stay for Type 2 Diabetes Patients by Individual Hospital. Health, 8, 505-517.
http://dx.doi.org/10.4236/health.2016.86054 - 11. Nawata, K. and Kawabuchi, K. (2016) A Long Term Evaluation of the Japanese Medical Payment System for Cataract Surgeries: Did the Medical Policy Reduce the Long Hospital Stay in Japan? Health, 8, 905-919.
http://dx.doi.org/10.4236/health.2016.89094 - 12. Central Social Insurance Medical Council (2014) DPC taishou hyouin Junbi hyouin no kibo (heisei 26 nen 4gatsu 1 nichi) mikomi (Estimated Sizes of DPC Hospitals and Preparing Hospitals as of April 1st, 2014). (In Japanese)
- 13. Greene, W.H. (1997) Econometric Analysis. 3rd Edition, Prentice-Hall, Upper Saddle River, New Jersey.
- 14. Showalter, M.H. (1994) A Monte Carlo Investigation of the Box-Cox Model and a Nonlinear Least Squares Alternative. Review of Economics and Statistics, 76, 560-570.
http://dx.doi.org/10.2307/2109980 - 15. Nawata, K. (2013) A New Estimator of the Box-Cox Transformation Model Using Moment Conditions. Economics Bulletin, 33, 2287-2297.
- 16. Nawata, K. and Kawabuchi, K. (2014) A New Test for the Box-Cox Transformation Model: An Analysis of Length of Hospital Stay for Diabetes Patients in Japan Economics Bulletin, 34, 324-332.
- 17. Nawata, K. (2015) Robust Estimation Based on the Third-Moment Restriction of the Error Terms for the Box-Cox Transformation Model: An Estimator Consistent Under Heteroscedasticity. Economics Bulletin, 3, 1056-1064.