Open Journal of Statistics
Vol.06 No.06(2016), Article ID:72619,13 pages
10.4236/ojs.2016.66088
Local Polynomial Regression Estimator of the Finite Population Total under Stratified Random Sampling: A Model-Based Approach
Charles K. Syengo1, Sarah Pyeye1, George O. Orwa2, Romanus O. Odhiambo2
1Pan African University Institute for Basic Sciences, Technology and Innovation, Nairobi, Kenya
2Department of Statistics and Actuarial Science, Jomo Kenyatta University of Agriculture and Technology, Nairobi, Kenya

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 5, 2016; Accepted: December 3, 2016; Published: December 8, 2016
ABSTRACT
In this paper, auxiliary information is used to determine an estimator of finite population total using nonparametric regression under stratified random sampling. To achieve this, a model-based approach is adopted by making use of the local polynomial regression estimation to predict the nonsampled values of the survey variable y. The performance of the proposed estimator is investigated against some design- based and model-based regression estimators. The simulation experiments show that the resulting estimator exhibits good properties. Generally, good confidence intervals are seen for the nonparametric regression estimators, and use of the proposed estimator leads to relatively smaller values of RE compared to other estimators.
Keywords:
Sample Surveys, Stratified Random Sampling, Auxiliary Information, Local Polynomial Regression, Model-Based Approach, Nonparametric Regression

1. Introduction
Sample surveys’ main objective is to obtain information about the population, and then use such information to make inference about some population quantities. The information that is mostly sought about the population is usually aggregate values of various population characteristics, total number of units, proportion of units having certain attributes. The information can be collected by either sampling methods or census. One of the approaches to using auxiliary information in construction of estimators is by assuming a working model that describes the relationship between the survey variable and the auxiliary variable. Estimators are then derived based on this model. At this stage, estimators are sought to have good efficiency given that the model is true. In most cases, a linear model is assumed. Generalized regression estimators by [1] and [2] including linear regression estimators and ratio estimators by [3] , and best linear unbiased estimators by [4] and [5] and post-stratification estimators by [6] as well are all derived from the assumption of linear models. Sometimes the linear model fails, and therefore, the resulting estimators do not beat the purely design-based estimators. As a result, [7] proposed a class of estimators in which the working model assumes a nonlinear parametric model. The improvement of the efficiency of such estimators, however, requires prior information about the exact parametric population structure. As a result of these concerns, several researchers have so far considered nonparametric models for . Nonparametric regression may be used in the estimation of unknown finite population quantities such as population totals, means, proportions or averages. The idea of nonparametric regression traces its origin in works by [8] and [9] . Nonparametric-based estimation is often more robust and flexible than inference based on parametric regression models or design probabilities (as in designed-based inference) [10] . In sample surveys, auxiliary information is used at the estimation stage of finite population quantities-population total or mean, say-to increase the precision of estimators of such population quantities [11] [12] [13] .
. Nonparametric regression may be used in the estimation of unknown finite population quantities such as population totals, means, proportions or averages. The idea of nonparametric regression traces its origin in works by [8] and [9] . Nonparametric-based estimation is often more robust and flexible than inference based on parametric regression models or design probabilities (as in designed-based inference) [10] . In sample surveys, auxiliary information is used at the estimation stage of finite population quantities-population total or mean, say-to increase the precision of estimators of such population quantities [11] [12] [13] .
A variety of approaches exist for construction of more efficient estimators for population total or mean, and they include model-based and design-based methods. Model-based approach in sample surveys is based on superpopulation models, which assumes that the population under study is a realization of a random variable having a superpopulation model . This model
. This model 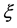 is used to predict the nonsampled values of the population, and hence the finite population quantities, total
is used to predict the nonsampled values of the population, and hence the finite population quantities, total 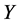 or mean
or mean 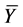 [13] . [14] first considered nonparametric models for
[13] . [14] first considered nonparametric models for 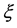 within a model-assisted approach and obtained a local polynomial regression estimator as a generalization of the ordinary generalized regression estimator. Their simulation study shows that the proposed estimator performs relatively better than other parametric estimators. [13] improved on [14] estimator and developed a model-based local polynomial regression estimator applicable to direct sampling designs such as simple random sampling and systematic sampling. Their estimator demonstrates better performance than [14] model-assisted estimator. Their estimator also beats other parametric estimators.
within a model-assisted approach and obtained a local polynomial regression estimator as a generalization of the ordinary generalized regression estimator. Their simulation study shows that the proposed estimator performs relatively better than other parametric estimators. [13] improved on [14] estimator and developed a model-based local polynomial regression estimator applicable to direct sampling designs such as simple random sampling and systematic sampling. Their estimator demonstrates better performance than [14] model-assisted estimator. Their estimator also beats other parametric estimators.
In this paper, auxiliary information is used to determine an estimator of finite population total using nonparametric regression under stratified random sampling. To achieve this, a model-based approach is adopted by making use of the local polynomial regression estimation to predict the nonsampled values of the survey variable y. Stratified estimators for finite population total 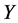 or mean
or mean 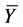 have proved to yield better estimators than those resulting from simple random sampling [15] [16] . Additionally, it has been shown in the literature that local polynomial approximation method has several nice features including satisfactory boundary behaviour, easy interpretability, applicability for a variety of design-circumstances and nice minimax properties (see [17] [18] and [19] ).
have proved to yield better estimators than those resulting from simple random sampling [15] [16] . Additionally, it has been shown in the literature that local polynomial approximation method has several nice features including satisfactory boundary behaviour, easy interpretability, applicability for a variety of design-circumstances and nice minimax properties (see [17] [18] and [19] ).
2. Proposed Estimator
Consider a population consisting of N units. Suppose this population is divided into H disjoint strata, each of size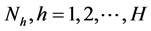 .
.
Let  be the survey measurement for the
be the survey measurement for the 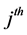 unit in the
unit in the  stra- tum. Further, let
stra- tum. Further, let 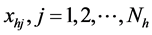 be the auxiliary measurement positively correlated with
be the auxiliary measurement positively correlated with .
.
From each stratum, a simple random sample of size 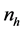 is selected without replace- ment, where
is selected without replace- ment, where 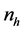 is sufficiently large with respect to
is sufficiently large with respect to  and
and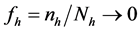 .
.
Let 



The population total is defined as

which can rewritten as

where 

Once the sample has been observed, the problem of estimating Y becomes the problem of predicting the sum of the nonsampled

The first component in Equation (1) is known while the second requires prediction which is the focus in this paper. In this paper, local polynomial regression method will be used to predict the unknown

Suppose the distribution generating 


where 

Then it follows that


where 


In practice, the values of 


Then a model-based local polynomial regression estimator of the nonsampled 


where 




holds as long as 
Now denoting the estimator for the finite population total by 



and the estimator for the finite population total is

with
3. Properties of Proposed Estimator
In this section, a study is carried out on various properties of estimator (8), which may be important in practice. In doing so, the following assumptions are made:
1) The regression function 
2) The marginal density, 

3) The conditional variance 
4) The kernel density function 
following:


for
These conditions on 
3.1. 
Now consider the difference:



and taking expectation yields


since
i.e.

which is the bias associated with
Approximating 




Letting


and applying expectations then

Theorem 3 of [21] allows that under conditions (1)-(4) if 



So that

It implies that 



3.2. Mean Square Error (MSE) of
The estimator (8) has the MSE

which can be decomposed as

Theorem 1 of [18] allows that under Condition (1), if 

Observe that Equation (24) tends to zero if 


This shows that 
4. Simulation Study
In this section, a study is carried out on the practical performance of several estimators (see Table 1 and Table 2 for the estimators).
The first estimator is design-based, the second one is parametric and model-based while the last two are nonparametric and model-based.
4.1. Description of the Population
The working model is taken to be







with






The errors are assumed to be independent and identically distributed (i.i.d) normal random variables having mean 0 and standard deviation

Table 1. Estimators being compared in the Simulation study.
Figure 1. Plot of linear, sine, bump and jump populations.
population values 





Epanechnikov kernel,

is used for kernel smoothing on each of the populations. In each case, bandwidth values 




Data simulations, the estimators and computations were obtained using R Software on a desktop.
To analyze the performance of the proposed estimator against some specified estimators, relative absolute bias (RAB) is computed as

and the relative efficiency (RE) with respect to the Horvitz-Thompson (HT) estimator is computed as


The relative efficiency (RE) is meant to examine the robustness of the various estimators against the proposed estimator.
The confidence intervals (CI) and the average lengths (AL) of the confidence intervals of various estimators are also computed as follows:


where 


4.2. Results
The results of this simulation study are summarized in Table 3 and Table 4. For each populations, 








Table 2. Summary of the formulae used in computing the respective population totals of the various estimators.
The confidence intervals and average length of the intervals are also measured for each case. A smaller length is better because it implies that the true population total is captured within a smaller range and therefore results are more precise.
The estimators 






Table 3 shows the RAB’s and RE’s of the various estimators with respect to the Horvitz-Thompson estimator (
In most scenarios, 


When the model is completely misspecified as in the Sine and Jump populations, a greater efficiency can be achieved by the nonparametric regression estimators. This can be seen in Table 3 for the Sine and Jump populations: the nonparametric estimators (


When the underlying superpopulation model is completely unknown, a reasonable choice for finite population total estimation would be the nonparametric estimators such as 

In this study, 



Despite 
Table 3. Relative absolute bias (RAB) and relative efficiency (RE) based on 1000 replications of simple random sampling within strata from four fixed populations of size

Table 4. Estimated lower and upper confidence limits and corresponding average lengths based on 1000 replications of simple random sampling within strata from four fixed populations of size

Additionally, a keen look at the estimated totals in Table 3 shows that: as the bandwidth increases, the local linear regression estimator, 









5. Conclusion
In this study, performance of the proposed estimator has been investigated against some design-based and model-based regression estimators. The RE values of the proposed estimator are in general close to one. It has been shown that for whichever bandwidth considered, 




Acknowledgements
Special thanks to the African Union (AU) for the funding that saw the success of this research.
Cite this paper
Syengo, C.K., Pyeye, S., Orwa, G.O. and Odhiambo, R.O. (2016) Local Polynomial Regression Estimator of the Finite Population Total under Stratified Random Sampling: A Model- Based Approach. Open Journal of Statistics, 6, 1085-1097. http://dx.doi.org/10.4236/ojs.2016.66088
References
- 1. Cassel, C.M., Sarndal, C.E. and Wretman, J.H. (1976) Some Results on Generalized Difference Estimation and Generalized Regression Estimation for Finite Populations. Biometrika, 63, 615-620.
- 2. Robinson, P.M. and Sarndal, C.E. (1983) Asymptotic Properties of the Generalized Regression Estimation in Probability Sampling. The Indian Journal of Statistics, Series B, 45, 240-248.
- 3. Cochran, W.G. (1977) Sampling Techniques. J. Wiley, New York.
- 4. Royall, R.M. (1970) On Finite Population Sampling Theory under Certain Linear Regression Models. Biometrika, 57, 377-387.
- 5. Brewer, K.R.W. (1963) Ratio Estimation in Finite Populations: Some Results Deductible from the Assumption of an Underlying Stochastic Process. Australian Journal of Statistics, 5, 93-105.
- 6. Holt, D. and Smith, T.M. (1979) Post Stratification. Journal of the Royal Statistical Society, Series A, 142, 33-46.
- 7. Wu, C.B. and Sitter, R.R. (2001) A Model-Calibration Approach to Using Complete Auxiliary Information from Survey Data. Journal of the American Statistical Association, 96, 185-193.
- 8. Nadaraya, E.A. (1964) On Estimating Regression. Theory of Probability and Applications, 9, 141-142.
- 9. Watson, G.S. (1964) Smooth Regression Analysis. Sankhya, Series A, 359-372.
- 10. Dorfman, A.H. (1992) Nonparametric Regression for Estimating Totals in Finite Population. In Section on Survey Research Methods. Journal of American Statistical Association, 622-625.
- 11. Montanari, G.E. and Ranalli, M.G. (2003) Nonparametric Methods in Survey Sampling. In: Vinci, M., Monari, P., Mignani, S. and Montanari, A., Eds., New Developments in Classification and Data Analysis, Springer, Berlin, 203-210.
- 12. Montanari, G.E. and Ranalli, M.G. (2005) Nonparametric Model Calibration Estimation in Survey Sampling. Journal of the American Statistical Association, 100, 1429-1442.
https://doi.org/10.1198/016214505000000141 - 13. Sanchez-Borrego, I.R. and Rueda, M. (2009) A Predictive Estimator of Finite Population Mean Using Nonparametric Regression. Computational Statistics, 24, 1-14.
https://doi.org/10.1007/s00180-008-0140-x - 14. Breidt, F.J. and Opsomer, J.D. (2000) Local Polynomial Regression Estimators in Survey Sampling. The Annals of Statistics, 28, 1026-1053.
- 15. Orwa, G.O., Otieno, R.O. and Mwita, P.N. (2010) Nonparametric Mixed Ratio Estimator for a Finite Population Total in Stratified Sampling. Pakistan Journal of Statistics and Operation Research, 4, 21-35.
https://doi.org/10.18187/pjsor.v6i1.149 - 16. Ngesa, O.O., Orwa, G.O., Otieno, R.O. and Murray, H.M. (2012) Multivariate Ratio Estimator of the Population Total under Stratified Random Sampling. Open Journal of Statistics, 2, 300-304.
https://doi.org/10.4236/ojs.2012.23036 - 17. Fan, J. and Gijbels, I. (1992) Variable Bandwidth and Local Linear Regression Smoothers. The Annals of Statistics, 20, 2008-2036.
https://doi.org/10.1214/aos/1176348900 - 18. Fan, J. (1993) Local Linear Regression Smoothers and Their Minimax Efficiencies. The Annals of Statistics, 21, 196-216.
https://doi.org/10.1214/aos/1176349022 - 19. Ruppert, D. and Wand, M.P. (1994) Multivariate Locally Weighted Least Squares Regression. The Annals of Statistics, 22, 1346-1370.
https://doi.org/10.1214/aos/1176325632 - 20. Rady, E.-H.A. and Ziedan, D. (2014) Estimation of Population Total Using Local Polynomial Regression with Two Auxiliary Variables. Journal of Statistics Applications & Probability, 3, 129-136.
https://doi.org/10.12785/jsap/030203 - 21. Fan, J. and Gijbels, I. (1996) Local Polynomial Modelling and Its Applications. Chapman and Hall, London.
- 22. Horvitz, D.G. and Thompson, D.J. (1952) A Generalization of Sampling without Replacement from a Finite Universe. Journal of American Statistical Association, 47, 663-685.
https://doi.org/10.1080/01621459.1952.10483446







