Open Journal of Statistics
Vol.05 No.07(2015), Article ID:62044,12 pages
10.4236/ojs.2015.57074
Short Term Forecasting Performances of Classical VAR and Sims-Zha Bayesian VAR Models for Time Series with Collinear Variables and Correlated Error Terms
M. O. Adenomon*, V. A. Michael, O. P. Evans
Department of Mathematics & Statistics, The Federal Polytechnic, Bida, Nigeria
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 August 2015; accepted 15 December 2015; published 18 December 2015
ABSTRACT
Forecasts can either be short term, medium term or long term. In this work, we consider short term forecast because of the problem of limited data or time series data that often encounter in time series analysis. This simulation study considers the performances of the classical VAR and Sims-Zha Bayesian VAR for short term series at different levels of collinearity and correlated error terms. The results from 10,000 iteration reveal that the BVAR models are excellent for time series length of T = 8 for all levels of collinearity while the classical VAR is effective for time series length of T = 16 for all collinearity levels except when ρ = −0.9 and ρ = −0.95. Therefore, we recommend that for effective short term forecasting, the time series length, forecasting horizon and the collinearity level should be considered.
Keywords:
Short term, Forecasting, Vector Autoregressive (VAR), Bayesian VAR (BVAR), Sims-Zha Prior, Collinearity, Error Terms

1. Introduction
Forecasts from classical Vector Autoregression (VAR) models and the Bayesian VAR had gained great popularity in the 1980s ([1] [2] ). In recent times, the classical VAR models tend to over fit the data and overestimate the magnitude of the coefficients of distant lags of variables as a result of sampling error [3] . But the Bayesian VAR is designed to improve macroeconomic forecast and to solve many problems associated with the classical VAR. The many advantages of the BVAR make it more useful in forecasting short term macroeconomic series. As observed by Bischoff et al., [2] that a small VAR, Bayesian or otherwise, can be useful for the purpose of forecast only.
Forecast can either be short term, medium term or long term. In this present work, our focus is on short term forecast because of the problem of limited data or time series that may be encountered in time series analysis.
Short term forecasting is very useful for decision making in many fields of life. [4] uses the Bayesian VAR to model and forecast the intraday electricity load in the short term. [5] considers short term load forecasting methods based on European data, while [6] [7] and [8] use different statistical models to forecast GDP in their respective countries. [9] uses factor models for short term forecasting of the Japanese economy; [10] considers factors affecting short term load forecasting and, [11] in their review considers short term weather forecasting from the physic and mathematics point of view. For other examples on short term forecasting see [12] [13] and [14] .
This present work is motivated by the work of Johnson, [15] who studies the effect of correlation and identification status on methods of estimating parameters of system of simultaneous equations using Monte Carlo approach. Also the work of Bischoff, Balay and Kang, [2] give rise to this present work. Bischoff, Balay and Kang suggest that if one only wants to forecast (i.e. not do “structural analysis”) a small VAR, Bayesian, otherwise, can be useful. Lastly this work is also motivated by the recent work by Dormann et al., [16] who observe in their simulation studies on GLM that correlation coefficient of
 is an appropriate indicator when collinearity begins to severely distort model estimation and subsequent prediction.
is an appropriate indicator when collinearity begins to severely distort model estimation and subsequent prediction.
Therefore, the aim of this paper is to compare the performances of the classical VAR and Bayesian VAR for time series with collinear variables and correlated error terms in the short term.
2. Review of Related Literatures
The name “multicollinearity” was first introduced by Ragnar Frisch. In his original formulation the economic variables are supposed to be composed of two parts, a systematic or “true” and an “error” component. This problem which arise when some or all the variables in the regression equation are highly intercorrelated and it becomes also impossible to separate their influences and obtain the corresponding estimates of the regression coefficient [17] . Multicollinearity is a term that refers to correlation among independent variables in a multiple regression model; it is usually invoked when some correlations are “large” but an actual magnitude test is not well defined [18] .
[19] proposed a statistic that measure the ‘distance’ of a cross-product matrix from the diagonal matrix obtained by zeroing its off-diagonal elements and they found it useful in detecting near multicollinearity regression problems. It can also distinguished between apparent and real multicollinearity with positive probability.
[20] worked out the statistical implications of the orthogonalization procedure in the general linear model. His work demonstrated that orthogonalization can worsen collinearity if measured by its effect on estimated variances.
[21] reported that parameter estimates may be poorly determined in-sample due to the sheer number of variables, perhaps worsened by the high degree of collinearity manifested in the levels of integrated data.
[22] investigated the non-uniqueness of collinearity using the static regression model and reported that any collinearity in the explanatory variables is irrelevant to forecasting so long as the marginal process remains constant.
[23] noted that since non-experimental data in general and economics data in particular, are often highly correlated, then from Bayesian viewpoint model specification is closely related to the problem of multicollinearity. In their approach they compared the predictive densities for an equation with and without the set of variables in question in order to gauge that the set may be safely omitted if the omission has little or no effect on the predictive densities. They concluded that examination of changes in predictive means and of Generalized Variance Ratio (GVR) is a useful method of investigation model specification.
[24] revealed through their Monte Carlo simulation experiment that multicollinearity can cause problems in theory testing (Type II errors) under certain conditions which includes: when multicollinearity is extreme; when multicollinearity is between 0.6 and 0.8, and when multicollinearity is between 0.4 and 0.5.
[25] studied graphical views of suppressor variables and multicollinearity in multiple linear regression.
[26] investigated the Type II error rate of the OLS estimators at different levels of multicollinearity and sample sizes through Monte-Carlo studies. Their work revealed that increasing the sample size reduces the type II error rate of the OLS estimator at all levels of multicollinearity.
[27] considered the available options available to researchers when one or more assumptions of an ordinary Least Squares (OLS) regression model are violated. Ayyangar paid particular attention on the problems of skewness, multcollinearity and heteroskedasticity and autocorrelated error terms on OLS models using SAS with illustration to health care cost data.
[15] studied the effects of correlation and identification status on methods of estimating parameters of system of simultaneous equations model using Monte Carlo approach. The Monte Carlo approach for the performances of the estimating methods at different levels of correlation, sample sizes and identification status were reported.
[28] considered the various performances of Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) and Mallow Cp statistic in the presence of a multicollinear regression using simulated data from SAS programme. Their work revealed that the performances of AIC and BIC in choosing the correct model among collinear variables are better when compared with the performances of Mallow’s Cp.
[29] studied the effects of multicollinearity and the sensitivity of the estimation methods in simultaneous equation model for different levels of different levels of multicollinearity. He considered Ordinary Least Squares (OLS), 2 Stage Least Squares (2SLS) and 3 Stage Least Squares (3SLS) methods of estimation. His result revealed preference of 3SLS over 2SLS and OLS.
[30] noted that multicollinearity problems are almost always present in time-series data generated by natural experiments. He also noted that multicollinearity becomes “harmful” when there is an R2 in the predictor matrix that is of the same order of magnitude as the R2 of the overall model.
[31] studied the effect of multicollinearity on some estimators (Ordinary Least Squares, Cochran-Orcut (GLS2), Maximum Likelihood Estimator (MLE), Multivariate Regression, Full Information Maximum Likelihood, Seemingly Unrelated Regression (SUR) and Three Stage Least Squares (3SLS)). Results showed that multivariate regression, FIML, SUR and 3SLS estimators are preferred at all levels of sample size.
[32] studied the performances of Bayesian Linear regression, Ridge Regression and OLS methods for modeling collinear data.
[16] who observed in their simulation studies on GLM that correlation coefficient of
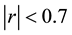 was an appropriate indicator for when collinearity begins to severely distort model estimation and subsequent prediction.
was an appropriate indicator for when collinearity begins to severely distort model estimation and subsequent prediction.
[33] compared the forecasting performances of the Reduced form Vector Autoregression (VAR) and Sims- Zha Bayesian VAR (BVAR) in a situation where the endogenous variables are collinear at different levels and at different short terms time series lengths assuming harmonic decay.
Sources of multicollinearity includes: the data collection method employed; constraints on the model or in the population being sampled; model specification; and overdetermined model. Multicollinearity especially in time series data may occur if the regressors included in the model share a common trend, that is, they all increase or decrease over time.
[34] identified some consequences of multicollinearity. They include:
1) Although BLUE, the OLS estimators have large variances and covariances making precise estimation difficult.
2) Because of consequence 1, the confidence interval tends to be much wider, leading to the acceptance of the (zero null hypothesis) and the t-ratio of one or more coefficients tends to be statistically insignificant.
3) Although the t-ratio of one or more coefficients is statistically insignificant, R2, the overall measure of goodness-of-fit can be very high.
4) The OLS estimators and their standard errors can be sensitive to small change in the data.
3. Model Description
3.1. Vector Autoregression (VAR) Model
VAR methodology superficially resembles simultaneous equation modeling in that we consider several endogenous variables together. But each endogenous variable is explained by its lagged values and the lagged values of all other endogenous variables in the model; usually, there are no exogenous variables in the model [34] .
Given a set of k time series variables,
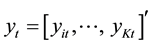 , VAR models of the form
, VAR models of the form
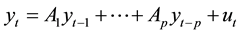 (1)
(1)
provide a fairly general framework for the Data General Process (DGP) of the series. More precisely this model is called a VAR process of order p or VAR(p) process. Here
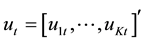 is a zero mean independent white noise process with non singular time invariant covariance matrix ∑u and the Ai are (k ´ k) coefficient matrices. The process is easy to use for forecasting purpose though it is not easy to determine the exact relations between the variables represented by the VAR model in Equation (1) above [35] . Also, polynomial trends or seasonal dummies can be included in the model.
is a zero mean independent white noise process with non singular time invariant covariance matrix ∑u and the Ai are (k ´ k) coefficient matrices. The process is easy to use for forecasting purpose though it is not easy to determine the exact relations between the variables represented by the VAR model in Equation (1) above [35] . Also, polynomial trends or seasonal dummies can be included in the model.
The process is stable if
 (2)
(2)
In that case it generates stationary time series with time invariant means and variance covariance structure.
Therefore To estimate the VAR model, one can write a VAR(p) with a concise matrix notation as
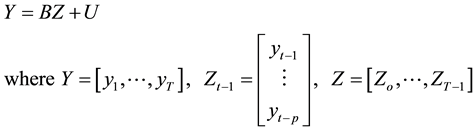 (3)
(3)
Then the Multivariate Least Squares (MLS) for B yields
 (4)
(4)
It can be written alternatively as
 (5)
(5)
where
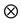 denotes the Kronecker product and Vec the vectorization of the matrix Y. This estimator is consistent and asymptotically efficient. It furthermore equals the conditional Maximum Likelihood Estimator (MLE) [36] .
denotes the Kronecker product and Vec the vectorization of the matrix Y. This estimator is consistent and asymptotically efficient. It furthermore equals the conditional Maximum Likelihood Estimator (MLE) [36] .
As the explanatory variables are the same in each equation, the multivariate least squares is equivalent to the Ordinary Least Squares (OLS) estimator applied to each equation separately, as was shown by [37] .
In the standard case, the MLE estimator of the covariance matrix differs from the OLS estimator.
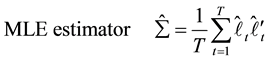 (6)
(6)
OLS estimator for a model with a constant, k variables and p lags, in a matrix notation, gives
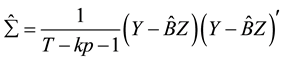 (7)
(7)
Therefore, the covariance matrix of the parameters can be estimated as
 (8)
(8)
3.2. Bayesian Vector Autoregression with Sims-Zha Prior
In recent times, the BVAR model of [38] has gained popularity both in economic time series and political analysis. The Sims-Zha BVAR allows for a more general specification and can produce a tractable multivariate normal posterior distribution. Again, the Sims-Zha BVAR estimates the parameters for the full system in a multivariate regression [3] .
Given the reduced form model
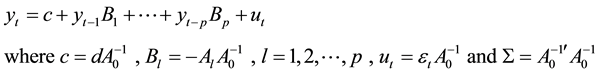
The matrix representation of the reduced form is given as
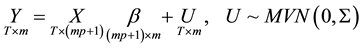
We can then construct a reduced form Bayesian SUR with the Sims-Zha prior as follows. The prior means for the reduced form coefficients are that B1 = I and
This representation translates the prior proposed by Sims-Zha form from the structural model to the reduced form ([3] [39] and [38] [40] ).
The summary of the Sims-Zha prior is given in Table 1.
3.3. Simulation Procedure
The simulated data will be generated for time series lengths of 8 and 16. The choice of the length chosen is to be able to study the models in the short run [41] . This study also considered ten (10) multicollinearity levels as ρ =(0.8, −0.8, 0.85, −0.85, 0.9, −0.9, 0.95, −0.95, 0.99, −0.99).
The simulation procedure is given in the following steps.
Step1: we generated a VAR (2) process that obeys the following form
Our choice for this form model is to obtain a stable process and a VAR process that is not affected by overparameterization [8] .
Step2: let the desired correlation matrix be


Step 3: the VAR and BVAR models of lag length of 2 was be used for modeling and forecasting simulated data to obtain the RMSE and MAE.
Step 4: Step 1 to Step 3 was repeated for 10,000 times, and the averages of the criteria were used to access the preferred model. A sample of simulated data is presented in Table 2 below.
Table 1. Hyperparameters of Sims-Zha reference prior.
Source: Brandt and Freeman, [3] .
Table 2. Sample of Simulated data for T = 16.
3.4. Model Specification
The time series were generated data using a VAR model with lag 2. The choice here is to obtain a bivariate time series with the true lag length. While the VAR and BVAR models of lag length of 2 will be used for modeling and forecasting purpose.
For the BVAR model with Sims-Zha prior, we will consider the following range of values for the hyperparameters given below and the Normal-Inverse Wishart prior.
We consider two tight priors and two loose priors as follows:
where nμ is prior degrees of freedom given as m + 1 where m is the number of variables in the multiple time series data. In work nμ is 3 (that is two (2) time series variables plus 1(one)).
The choice of Normal-inverse Wishart prior for the BVAR models follow the work of [42] that Normal Wishart prior tends to performed better when compared to other priors. In addition [38] proposed Normal-Inverse Wishart prior because of its suitability for large systems while [43] reported that the most advantage of Wishart distribution is that it guaranteed to produce positive definite draws. Our choice of the overall tightness

The following are the criteria for forecast assessments used:
1) Mean Absolute Error (MAE) has a formular
series in absolute terms, and measures how much the forecast is biased. This measure is one of the most common ones used for analyzing the quality of different forecasts.
2) The Root Mean Square Error (RMSE) is given as

For the two measures above, the smaller the value, the better the fit of the model [48] .
In this simulation study,

3.5. Statistical Packages (R)
In this study three procedures in the R package will be used. They are: Dynamic System Estimation (DSE) [49] ; the vars [50] : and the MSBVAR [51] .
4. Results and Discussion
The results from the analysis are presented in Tables 3-5. The values of the RMSE and MAE are presented in Table 3. Generally the values of the RMSE and MAE decrease as a result of increase in the time series length from 8 to 16. Also the values of the RMSE and MAE increase as the collinearity values increases.
Table 3. Forecasting performances of the models for different time series length and forecasting horizons at different levels of collinearity.
In Table 4 below, we present the ranks of the performances of the model. Rank of 1 is assigned to the model with the smallest values of RMSE and MAE while rank of 5 is assigned to the model with the largest values of the RMSE and MAE.
In Table 5 below, we present the preferred model for the different time series length and forecasting horizons at the different collinearity levels. It was observed that from ρ = −0.95 to ρ = −0.8 for T = 8, the BVAR model with loose prior are preferred while for ρ = −0.99, the BVAR model with tight prior is preferred. For the positive collinearity from ρ = 0.8 to ρ = 0.99 for T = 8, the BVAR model with tight prior are preferred. In general for T = 8, the BVAR model with loose prior are suitable for negative collinearity level while the BVAR model with tight prior are suitable for positive collinearity levels.
Also for time series length and forecasting horizon of T = 16, the classical VAR model is preferred for all the collinearity levels except for ρ = −0.95 and ρ = −0.9 where the BVAR model with loose prior are preferred.
5. Conclusion and Recommendation
The results from this study revealed that the BVAR models were excellent for time series length of T = 8 for all levels of collinearity while the classical VAR was effective for time series length of T = 16 for all collinearity
Table 4. Ranks of the performances of the models for different time series length and forecasting horizons at different levels of collinearity.
Table 5. Preferred models for different time series length and forecasting horizons at different levels of collinearity.
levels except when ρ = −0.9 and ρ = −0.95. Therefore, we recommended that for effective short term forecasting, the time series length, forecasting horizon and the collinearity level should be considered.
Acknowledgements
We wish to thank TETFUND Abuja-Nigeria for sponsoring this research work. Our appreciation also goes to the Rector and the Directorate of Research, Conference and Publication of the Federal Polytechnic Bida for giving us this opportunity to undergo this research work.
Cite this paper
M. O.Adenomon,V. A.Michael,O. P.Evans, (2015) Short Term Forecasting Performances of Classical VAR and Sims-Zha Bayesian VAR Models for Time Series with Collinear Variables and Correlated Error Terms. Open Journal of Statistics,05,742-753. doi: 10.4236/ojs.2015.57074
References
- 1. Sims, C.A. (1980) Macro Economics and Reality. Econometrica, 48, 1-48.
http://dx.doi.org/10.2307/1912017 - 2. Bischoff, C.W., Belay, H. and Kang, I.-B. (2000) Bayesian VAR Forecasts Fail to Live up to Their Promise: For the Period 1981-1996. Judgementally Adjusted Large Structural Macroeconomic Models Forecast More Accurately than Bayesian VAR Models. Business Economics, 35, 19-29.
- 3. Brandt, P.T. and Freeman, J.R. (2006) Advances in Bayesian Time Series Modeling and the Study of Politics: Theory, Testing, Forecasting and Policy Analysis. Political Analysis, 14, 1-36.
http://dx.doi.org/10.1093/pan/mpi035 - 4. Cottet, R and Smith, M. (2003) Bayesian Modelling and Forecasting of Intraday Electricity Load. Journal of the American Statistical Association, 98, 839-849.
http://dx.doi.org/10.1198/016214503000000774 - 5. Taylor, J.M. and Mcsharry, P.E. (2008) Short Term Load Forecasting Methods: An Evaluation Based on European Data. IEEE Transactions on Power System, 22, 2213-2219.
http://dx.doi.org/10.1109/TPWRS.2007.907583 - 6. Lacoviello, M. (2001) Short Term Forecasting: Projecting Italian GDP, One Quarter to Two Years Ahead. IMF Working Paper No. WP/01/109.
- 7. Karim, B., Szilard, B., Riccardo, C., Ard, D.R., Audrone, J., Pioyr, J., Antonio, R., Gerhard, R., Karsten, R. and Christophe, V.N. (2008) Short Term Forecasting of GDP Using Large Monthly Data Sets. A Pseudo Real Time Forecast Evaluation Exercise. Occassional Paper Series No. 84, European Central Bank.
- 8. Caraiani, P. (2010) Forecasting Romanian GDP Using a BVAR Model. Romanian Journal of Economic Forecasting, 4, 76-87
- 9. Godbout, C. and Lombardi, M.J. (2012) Short Term Forecasting of the Japanese Economy Using Factor Model. Working Paper Series No. 1428, European Central Bank.
- 10. Fahab, M.U. and Arbab, M.N. (2014) Factor Affecting Short Term Load Forecasting. JCET, 2, 305-309.
- 11. Belousov, S.L. and Berkovich, L.V. (2015) Short Term Weather Forecasting. Environmental Structure and Function: Climate System—Volume I, EOLSS.
http://www.ecolss.net/Eolss-sampleAllchapter.aspx - 12. Gorr, W., Olligschlaeger, A. and Thompson, Y. (2003) Short Term Forecasting of Crime. International Journal of Forecasting, 19, 579-594.
http://dx.doi.org/10.1016/S0169-2070(03)00092-X - 13. Melihovs, A. and Rusakova, S. (2005) Short Term Forecasting of Economic Development in Latvia Using Business and Consumer Survey Data. Working Paper No. 4, RIGA.
- 14. Da, Z. and Warachka, M. (2011) The Disparity between Long Term and Short Term Forecasted Earnings Growth. Journal of Financial Economics, 100, 424-442.
http://dx.doi.org/10.1016/j.jfineco.2010.10.015 - 15. Johnson, T.L. (2009) Effect of Correlation and Identification Status on Methods of Estimating Parameters of System of Simultaneous Equations Model. Unpublished PhD Thesis, University of Ilorin, Ilorin.
- 16. Dormann, C.F., Elith, J., Bacher, S., Bachmann, C., Carl, G., Lagourcade, B., Leifao, P.J., Munkemiller, T., McClean, C., Osborne, P.E., Reineking, B., Schroder, B., Skidmore, A.K., Jurell, D. and Lautenbach, S. (2013) Collinearity: A Review of Methods to Deal with It and a Simulation Study Evaluating Their Performance. Ecography, 36, 27-46.
http://dx.doi.org/10.1111/j.1600-0587.2012.07348.x - 17. Rama-Sastry, M.V. (1970) Some Limits in the Theory of Multicollinearity. The American Statistician, 24, 39-40.
- 18. Gunasekara, F.I., Carter, K. and Blakely, T. (2008) Glossary for Econometrics and Epidemiology. Journal of Epidemiology and Community Health, 62, 858-861.
http://dx.doi.org/10.1136/jech.2008.077461 - 19. Mehta, J.S., Swamy, P.A.V.B. and Iyengar, N.S. (1993) Finite Sample Properties of a Measure of Multicollinearity. Sankhya: The Indian Journal of Statistics B, 55, 353-371.
- 20. Buse, A. (1994) Brickmaking and the Collinear Arts: A Cautionary Tale. The Canadian Journal of Economics, 27, 408-414.
http://dx.doi.org/10.2307/135754 - 21. Clement, M.P. and Hendry, D.F. (1995) Macro-Economic Forecasting and Modelling. The Economic Journal, 105, 1001-1013.
http://dx.doi.org/10.2307/2235166 - 22. Hendry, D.F. (1997) The Econometrics of Macroeconomic Forecasting. The Economic Journal, 107, 1330-1357.
http://dx.doi.org/10.1111/j.1468-0297.1997.tb00051.x - 23. Greenberg, E. and Parks, R.P. (1997) A Predictive Approach to Model Selection and Multicollinearity. Journal of Applied Econometrics, 12, 67-75.
http://dx.doi.org/10.1002/(SICI)1099-1255(199701)12:1<67::AID-JAE427>3.0.CO;2-W - 24. Grewal, R., Cote, J.A. and Baumgartner, H. (2004) Multicollinearity and Measurement Error in Structural Equation Models: Implication for Theory Testing. Marketing Science, 23, 519-529.
http://dx.doi.org/10.1287/mksc.1040.0070 - 25. Friedman, L. and Wall, M. (2006) Graphical Views of Suppression and Multicollinearity in Multiple Linear Regression. The American Statistician, 59, 127-136.
http://dx.doi.org/10.1198/000313005X41337 - 26. Alabi, O.O., Ayinde, K. and Oyejola, B.A. (2007) Empirical Investigation of Effect of Multicollinearity on Type II Error Rates of the Ordinary Least Squares Estimators. Journal of the Nigerian Statistical Association, 19, 50-57.
- 27. Ayyangar, L. (2007) Skewness, Multicollinearity, Heteroskedasticity—You Name It, Cost Data Have It! Solutions to Violations of Assumptions of Ordinary Least Regression Models Using SAS. SAS Global Forum, Orlando, 16-19 April 2007.
- 28. Ijomah, M.A. and Nduka, E.C. (2010) Selection in a Multicollinear Data Using Information Criteria. Journal of the Nigerian Statistical Association, 22, 64-75.
- 29. Agunbiade, D.A. (2011) Effect of Multicollinearity and Sensitivity of the Methods in Simultaneous Equation Model. Journal of Modern Mathematics and Statistics, 5, 9-12.
http://dx.doi.org/10.3923/jmmstat.2011.9.12 - 30. Taylor, L.D. (2012) A Note on the Harmful Effects of Multicollinearity.
www.econ.arizona.edu/docs/Working_Papers/2012/Econ-WP-12-14.pdf - 31. Olanrewaju, S.O. (2013) Effect of Multicollinearity of Some Estimators of System of Regression Equations. Proceedings of the 32nd Annual Conference of the Nigerian Mathematical Society, Obafemi Awolowo University, Nigeria, 25-28 June 2013, 79.
- 32. Yahya, W.B. and Olaniran, O.R. (2013) Bayesian Linear Regression, Ridge Regression and Ordinary Least Squares Methods for modeling Collinear Data. Proceedings of the 32nd Annual Conference of the Nigerian Mathematical Society, Obafemi Awolowo University (OAU), 25-28 June 2013, 74.
- 33. Adenomon, M.O. and Oyejola, B.A. (2014) A Simulation Study of Effects of Collinearity on Forecasting of Bivariate Time Series Data. Scholars Journal of Physics, Mathematics and Statistics, 1, 4-21.
- 34. Gujarati, D.N. (2003) Basic Econometrics. 4th Edition, The McGraw-Hill Co., New Delhi.
- 35. Lütkepohl, H. and Breitung, J. (1997) Impulse Response Analysis of Vector Autoregressive Processes. In: Heij, C., Schumacher, H., Hanzon, B. and Praagman, C., Eds., System Dynamics in Economic and Financial Models, John Wiley, New York.
- 36. Hamilton, J.D. (1994) Time Series Analysis. Princeton University Press, Princeton.
- 37. Zeller, A. (1962) An Efficient Method of Estimating Seemingly Unrelated Regression and Tests for Aggregation Bias. Journal of the American Statistical Association, 57, 348-368.
http://dx.doi.org/10.1080/01621459.1962.10480664 - 38. Sims, C.A. and Zha, T. (1998) Bayesian Methods for Dynamic Multivariate Models. International Economic Review, 39, 949-968.
http://dx.doi.org/10.2307/2527347 - 39. Brandt, P.T. and Freeman, J.R. (2009) Modeling Macro-Political Dynamics. Political Analysis, 17, 113-142.
http://dx.doi.org/10.1093/pan/mpp001 - 40. Sims, C.A. and Zha, T. (1999) Error Bands for Impulse Responses. Econometrica, 67, 113-115.
http://dx.doi.org/10.1111/1468-0262.00071 - 41. Diebold, F.X. and Mariano, R.S. (2002) Comparing Predictive Accuracy. Journal of Business and Economic Statistics, 20, 134-144.
http://dx.doi.org/10.1198/073500102753410444 - 42. Kadiyala, K.R. and Karlsson, S. (1997) Numerical Methods for Estimation and Inference in Bayesian VAR Models. Journal of Applied Econometrics, 12, 99-132.
http://dx.doi.org/10.1002/(SICI)1099-1255(199703)12:2<99::AID-JAE429>3.0.CO;2-A - 43. Breheny, P. (2013) Wishart Priors. BST 701: Bayesian Modelling in Biostatistics.
http://web.as.uky.edu/statistics/users/pbreheny/701/S13/notes/3-28.pdf - 44. Brandt, P.T., Colaresi, M. and Freeman, J.R. (2008) Dynamic of Reciprocity, Accountability and Credibility. Journal of Conflict Resolution, 52, 343-374.
http://dx.doi.org/10.1177/0022002708314221 - 45. Merkin, J.H. and Needman, D.J. (1990) The Development of Travelling Waves in a Simple Isothermal Chemical System II. Cubic Autocatalysis with Quadratic and Linear Decay. Proceedings: Mathematical & Physical Sciences, 430, 315-345.
http://dx.doi.org/10.1098/rspa.1990.0093 - 46. Merkin, J.H. and Needman, D.J. (1991) The Development of Travelling Waves in a Simple Isothermal Chemical System IV. Quadratic Autocatalysis with Quadratic Decay. Proceedings: Mathematical & Physical Sciences, 434, 531-554.
http://dx.doi.org/10.1098/rspa.1991.0112 - 47. Worsley, K.J., Evans, A.C., Strother, S.C. and Tyler, J.L. (1991) A Linear Spatial Correlation Model with Applications to Positron Emission Tomography. Journal of the American Statistical Association, 86, 55-67.
http://dx.doi.org/10.1080/01621459.1991.10475004 - 48. Cooray, T.M.J.A. (2008) Applied Time series Analysis and Forecasting. Narosa Publising House, New Delhi.
- 49. Gilbert, P. (2009) Brief User’s Guide: Dynamic Systems Estimation (DSE).
www.bank-banque-canada.ca/pgilbert - 50. Pfaff, B. (2008) VAR, SVAR and SVEC Models: Implementation within R Package Vars. Journal of Statistical Software, 27, 1-32.
http://dx.doi.org/10.18637/jss.v027.i04 - 51. Brandt, P.T. (2012) Markov-Switching, Bayesian Vector Autoregression Models-Package “MSBVAR”. The R Foundation for Statistical Computing.
NOTES
*Corresponding author.






