Open Journal of Statistics
Vol.05 No.05(2015), Article ID:58780,9 pages
10.4236/ojs.2015.55046
On the Estimation of a Univariate Gaussian Distribution: A Comparative Approach
Cliff R. Kikawa*, Michael Y. Shatalov, Petrus H. Kloppers, Andrew C. Mkolesia
Department of Mathematics and Statistics, Tshwane University of Technology, Pretoria, South Africa
Email: *Richard.kikawa@gmail.com, *kikawaCR@tut.ac.za
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 June 2015; accepted 10 August 2015; published 13 August 2015
ABSTRACT
Estimation of the unknown mean, μ and variance, σ2 of a univariate Gaussian distribution 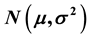 given a single study variable x is considered. We propose an approach that does not require initialization of the sufficient unknown distribution parameters. The approach is motivated by linearizing the Gaussian distribution through differential techniques, and estimating, μ and σ2 as regression coefficients using the ordinary least squares method. Two simulated datasets on hereditary traits and morphometric analysis of housefly strains are used to evaluate the proposed method (PM), the maximum likelihood estimation (MLE), and the method of moments (MM). The methods are evaluated by re-estimating the required Gaussian parameters on both large and small samples. The root mean squared error (RMSE), mean error (ME), and the standard deviation (SD) are used to assess the accuracy of the PM and MLE; confidence intervals (CIs) are also constructed for the ME estimate. The PM compares well with both the MLE and MM approaches as they all produce estimates whose errors have good asymptotic properties, also small CIs are observed for the ME using the PM and MLE. The PM can be used symbiotically with the MLE to provide initial approximations at the expectation maximization step.
given a single study variable x is considered. We propose an approach that does not require initialization of the sufficient unknown distribution parameters. The approach is motivated by linearizing the Gaussian distribution through differential techniques, and estimating, μ and σ2 as regression coefficients using the ordinary least squares method. Two simulated datasets on hereditary traits and morphometric analysis of housefly strains are used to evaluate the proposed method (PM), the maximum likelihood estimation (MLE), and the method of moments (MM). The methods are evaluated by re-estimating the required Gaussian parameters on both large and small samples. The root mean squared error (RMSE), mean error (ME), and the standard deviation (SD) are used to assess the accuracy of the PM and MLE; confidence intervals (CIs) are also constructed for the ME estimate. The PM compares well with both the MLE and MM approaches as they all produce estimates whose errors have good asymptotic properties, also small CIs are observed for the ME using the PM and MLE. The PM can be used symbiotically with the MLE to provide initial approximations at the expectation maximization step.
Keywords:
Mean Squared Error, Method of Moments, Maximum Likelihood Estimation, Regression Coefficients

1. Introduction
The Gaussian distribution is a continuous function characterized by the mean µ and variance σ2. It is regarded as the mostly applied distribution in all of the science disciplines since it can be used to approximate several other distributions. We consider a single observation x obtained from a univariate Gaussian distribution with both the mean µ and variance, σ2, unknown, that is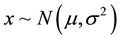 ,
, . In this paper the problems of estimating the sufficient parameters of a normal distribution using the iterative methods are discussed. We then propose an algorithm that mitigates the problems associated with the iterative techniques. A thorough discussion of the iterative techniques and their related algorithms can be obtained from [1] -[6] . The mean µ and the variance σ2 are referred to as sufficient parameters in most of the statistics literature and this is due to the fact that they contain all information about the probability distribution function, see Equation (1).
. In this paper the problems of estimating the sufficient parameters of a normal distribution using the iterative methods are discussed. We then propose an algorithm that mitigates the problems associated with the iterative techniques. A thorough discussion of the iterative techniques and their related algorithms can be obtained from [1] -[6] . The mean µ and the variance σ2 are referred to as sufficient parameters in most of the statistics literature and this is due to the fact that they contain all information about the probability distribution function, see Equation (1).
 (1)
(1)
An important problem in statistics is to obtain information about the mean, µ, and the variance, σ2 of a given population. The estimation of these parameters is central in areas such as machine learning, pattern recognition, neural networks, signal processing, computer vision and in feature extraction, see [6] - [11] .
The rationale and motivation for the proposed approach are presented in Section 2. The methodological steps and the datasets simulated to validate the proposed approach are discussed in Section 3. Explicit estimation steps using the ordinary least squares method are presented in Section 4. Statistical analysis results on simulations are presented in Section 5. The error distribution analyses are presented in Section 6. Accuracy results for the proposed method (PM) and maximum likelihood estimation (MLE) methods are presented in Section 7. In Sections 8 and 9 we provide a thorough discussion of the results and some concluding remarks on the study findings.
2. Rational and Motivation
Numerical methods for estimating parameters of a Gaussian distribution function are well known like the bisection method, Newton-Raphson, secant, false position, Gauss-Seidel, see [12] - [15] . Other methods for obtaining analytical solutions are, the maximum likelihood estimation (MLE), maximum distance estimation, maximum spacing estimation and moment-generating function method, see [16] - [18] . However, these approaches are largely dependent on guess initial values. The guess initial values may not guarantee convergence, could take a longer time or even fail to converge in case they are far from the optimal solution, hence requiring high expertise for their application, see [19] . The MLE is regarded as the standard approach to most of the nonlinear estimation problems as it always converges to the required minimum given “good” initial guess approximations, however, it requires the maximization of the log-likelihood method [20] . Application of the MLE procedure may present a challenge if necessary software is not available; it requires the applicant to have a mathematical background as it is necessary for the user to transform the likelihood function into its natural logarithm, referred to as the log-likelihood in most of the statistical literature. Since the maximum of the function is usually required, it is constrained that the derivative of the parent function is obtained a priori, and solving for the parameters being maximized. However, this can only be achieved by maximizing the log-likelihood function and not the parent function. Another difficulty is encountered at the initialization step, according to [21] : “One question that plagues all hill-climbing procedures is the choice of the starting point. Unfortunately, there is no simple, universally good solution to this problem.” as cited by [22] . We present a method for computing acceptable parameter values for the mean and variance that could be applied as initial guess values when the proposed approach is used symbiotically with the MLE.
3. Methodology
We transform the Gaussian density function (1) into a new function that is linear with respect to some of the unknown parameters or their combinations in an appropriate form. For linearization, we consider the derivatives for the parent function (1). The unknown regression parameters are then estimated using the ordinary least squares (OLS) methods. The employed frame-work was first proposed by [19] and has been used in the estimation of exponential functions; see [23] . We propose a version of this frame-work and use it to estimate the Gaussian distribution parameters. The PM is compared with both the MLE and MM the traditional estimation procedures on three simulations of normal datasets of known mean and standard deviation. The first two datasets are concerned with the study of hereditary physical characteristics see [24] in which both the father and daughter’s heights were studied. The third dataset was concerned with the morphometric analysis of DDT-resistant and non?resistant housefly strains, in which the housefly wing lengths are analyzed, see [25] . We estimate the known mean, µ, and standard deviation, σ, of the respective datasets using the three methods, that is the PM, MLE and MM.
In the course of estimation of the parameters using the PM, we anticipate that, there is a shift of the estimated parameters from their “true” values. The amount of this shift is what is commonly referred to as accuracy, and is computed as the difference between the known values and the estimates from the underlying process [26] . The distribution of the errors from the evaluated approaches is an important aspect that gives a clue on which assessment methods are to be employed, that is standard, visual or otherwise non parametric measures.
Transformation and Re-Characterization
It is always a requirement to estimate the parameters of a Gaussian distribution in most of the data modelling aspects involving normally distributed observations. In this section the method we present has not been considered before in the statistical literature that has been reviewed. The approach is to transform the original Gaussian function (1), and this is done by taking its first derivative and subsequently introducing new parameters either as linear or their combination.
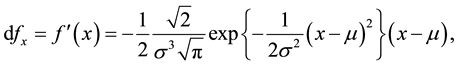 (2)
(2)
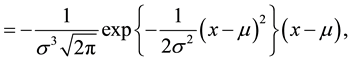 (3)
(3)
 (4)
(4)
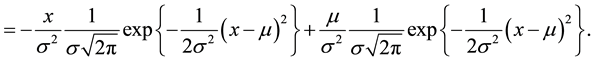 (5)
(5)
Re-arranging Equation (5)
 (6)
(6)
We observe from Equation (6) that the original function (1) is contained in both the first and second terms. Hence, we write Equation (6) as
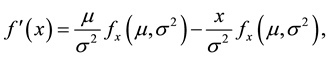 (7)
(7)
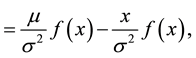 (8)
(8)
where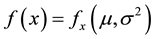 .
.
Introducing new parameters in Equation (8) to formulate a model linear in the new parameters, we obtain a simple linear model of the form
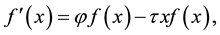 (9)
(9)
where 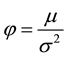 and
and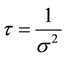 .
.
There are well-recognised approaches for obtaining the parameter, 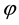 and
and 
1) Each of the independent variables (in this case
2) The model contians at most one unidentified parameter that does not have an independent variable.
3) All the discrete terms are summed to yield the ultimate model value [30] .
4. Estimation Criteria
Parameter estimation is an important aspect in most of the statistical modelling frame-works. The major goal of estimation is to obtain the numerical values of the regression coefficients associated with individual or a com- bination of the regressors [30] . For the proposed approach the estimation is as follows,
If a dataset say, 


be an estimation of 


We estimate the error, since it is known that an important part of estimation is the assessment of how much the computed value will vary due to noise in the dataset. When information concerning the deviations is not available, then there is no basis on which comparison of the estimated value to the “true” or target value can be done [30] .
The sum of squares of the errors over all the data points is



In Equation (14), variables 



So that,

as the goal function for the ordinary least sqaures estimation of the parameters 




The estimates of Gaussian distribution parameters are then estimated as

5. Method Evaluation
In oder to evaluate the performance of the proposed method (PM), we perform simulations of the father and daughters heights using Mathematica software [24] and compute their respective means and standard deviations, 


We now require to estimate the known means and standard deviations of the considered datasets using the PM, MLE and MM. The analysis is done on two samples, 

Table 1. Height of the father, required parameters, 
Table 2. Height of the daughter, required parameters, 
Table 3. Housefly wing lengths, required parameters, 
6. Error Distribution Analysis
We are frequently faced with a situation of processing volumes of data whose generative process we are uncertain about, yet it is always necessary to understand the sampling theory and statistcial inference before carrying out any parameter estimation in statistical modelling problems [30] . In this paper we consider perform- ing exploratory analysis on the error distribution as generated by each of the three evaluated approaches on esti- mating the “true” or required parameters 

6.1. Visualization of Normality
We aim at establishing the distribution of the errors from the PM in comparison to those from the standard method, that’s MLE. We would wish to use the easier standard statistical techniques like, the Pearson Chi- Square, the Jacque-berra, and the Kolmogorov-Smirnov methods to test for normality in the errors, but such tests are usually more receptive in case of large datasets. In that case visual methods have been preferred, see Figures 1-6, and these have several advantages [32] .
6.1.1. Histogram Plots
Error distribution can with little effort be observed by a histogram of the sampled errors, where the error counts are plotted. Such a histogram presents an overview of the normality of the error distribution, see Figures 1-6. For comparison with normality, normal distribution curves are superimposed on the histograms. The figures illu- strate the distribution of errors, 
Better diagnostic methods for checking deviations from a normal distribution are the so called quantile-quan- tile (Q-Q) plots, see [26] . Quantiles of empirical distribution functions are plotted against the hypothetical quantiles of the Gaussian distribution. For one to conclude that indeed the actual underlying distribution is Gaussian, the Q-Q plot should be able to yield a straight line. Observing Figure 3 and Figure 4 which are based on large samples, that is, 
Figure 1. Error distribution for the MLE on father’s height, expected counts μ = 0.15; σ = 0.09.
Figure 2. Error distribution for the PM on father’s height; expected counts μ = 0.11; σ = 0.09.
Figure 3. Normal Q-Q plot for the error (∆h) distribution from MLE on the father’s height, n = 1000.
Figure 4. Normal Q-Q plot for the error (∆h) distribution from PM on the father’s height, n = 1000.
Figure 5. Normal Q-Q plot for the error (∆h) distribution from MLE on the housefly wing lengths, n = 100.
Figure 6. Normal Q-Q plot for the error (∆h) distribution from PM on the housefly wing lengths, n = 100.
7. Accuracy Assessment
When normal distribution for the parent dataset, and no outliers are exhibited as shown in Section 6, then the accuracy measures in Table 4 can be adopted. The accuracy measures in the normal distribution fram-work are defines as follows
In Table 4, ∆hi denotes the difference between the observed and estimated value. Where i is the sampled data point, and n is the sample size. Assuming that the generated errors follow a normal distribution as established in Section 6, see Figures 1-6. Then from the theory of errors, it is well known that 68.3% of data will fall within the interval

Accuracy Results
Results generated by the standard measures of Table 4, are presented. We note that application of the standard measures impies that the generated errors follow a normal distribution as established in Section 6. Tables 5-8 show results for PM and MLE.
Tables 5-8 show the accuracy measures considered to evaluate the performance of the PM and the MLE, on two datasets of different sizes, that is 

8. Results and Discussion
The PM has been compared with some of the current methods in use that is, MM and MLE. These were preferred
Table 4. Measurement of accuracy for statistical methods presenting normally distributed errors.
Table 5. Measure of accuracy for the MLM approach; father’s height, n = 1000.
Table 6. Measure of accuracy for the PM approach; father’s height n = 1000.
Table 7. Measure of accuracy for the MLM approach; housefly wing lengths n = 100.
Table 8. Measure of accuracy for the PM approach on the housefly wing lengths (n = 100).
due to their computation lure and availability inmost of the statistical Software packages. Secondly the MLE method is more preferred and widely applied due to its good asymptotic properties. Three standard datasets from [24] and [25] have been used. However, on further tests only two datasets were considered, that is the height of the father and housefly wing lengths; this was to decrease on the intensity of the work to be presented.
Section 5, contains the computation results for PM, MM and MLE. Tables 1-3 illustrate and show the parameter estimates obtained from the methods. It is observed that all the approaches give comparable results with the “true” or required values of the parameters given in the captions of the respective tables.
In order to use standard techniques that are employed for accuracy measurements, the errors have been tested for normality, see Section 6. Statistical visualization techniques were preferred to other statistical tests which are said to be sensitive in the presence of outliers and large datasets [26] . Figure 1 and Figure 2 illustrate the histograms of the errors and clearly show a normal distribution since more of the information contained in the errors lies under the normal curve that is superimposed. The Q-Q plots in Figures 3-6 have also been used as a measure of testing for normality of the generated errors. It is observed that there are almost straight lines produced in all the cases. This implies that the actual distribution of the generated errors is indeed normally distributed.
9. Conclusion
This research laid out an easy approach to computing the parameters of a univariate normal distribution which is an important distribution in applied statistics and in most of the science disciplines. It serves as a platform or bench mark for studying more complex distributions, like the mixture of two or more Gaussians, mixture of exponentials and other continuous distributions which are very useful in pattern recognition, machine learning and unsupervised learning. The simplicity of the approach is time saving in computation and guarantees convergence to the required values, this is not usually the case in the conventional analytical and numerical methods as these may fail or take a long time to converge depending on the quality of initial approximations.
Acknowledgements
The authors wish to thank the Directorate of Research and Innovation of Tshwane University of Technology for funding the research under the Postdoctoral research fund 2014/2015. The anonymous reviewer and editors whose criticisms led to an improved version of the manuscript.
Cite this paper
Cliff R.Kikawa,Michael Y.Shatalov,Petrus H.Kloppers,Andrew C.Mkolesia, (2015) On the Estimation of a Univariate Gaussian Distribution: A Comparative Approach. Open Journal of Statistics,05,445-454. doi: 10.4236/ojs.2015.55046
References
- 1. Anita, H.M. (2002) Numerical Methods for Scientist and Engineers. Birkhauser-Verlag, Switzerland.
- 2. Baushev, A.N. and Morozova, E.Y. (2007) A Multidimensional Bisection Method for Minimizing Function over Simplex. Lectures Notes in Engineering and Computer Science, 2, 801-803.
- 3. Darvishi, M.T. and Barati, A. (2007) A Third-Order Newton-Type Method to Solve Systems of Nonlinear Equations. Applied Mathematics and Computation, 87, 630-635.
- 4. Jamil, N. (2013) A Comparison of Iterative Methods for the Solution of Non-Linear Systems of Equations. International Journal of Emerging Science, 3, 119-130.
- 5. Murray, W. and Overton, M.L. (1979) Steplength Algorithm for Minimizing a Class of Nondifferentiable Functions. Computing, 23, 309-331.
http://dx.doi.org/10.1007/BF02254861 - 6. Hornberger, G. and Wiberd, P. (2005) User’s Guide for: Numerical Methods in the Hydrological Sciences, in Numerical Methods in the Hydrological Sciences.
http://dx.doi.org/10.1002/9781118709528 - 7. Bishop, C.M. (1991) A Fast Procedure for Retraining the Multilayer Perceptron. International Journal of Neural Systems, 2, 229-236.
http://dx.doi.org/10.1142/S0129065791000212 - 8. Bishop, C.M. (1992) Exact Calculation of the Hessian Matrix for the Multilayer Perceptron. Neural Computation, 4, 494-501.
http://dx.doi.org/10.1162/neco.1992.4.4.494 - 9. Bishop, C.M. and Nabney, I.T. (2008) Pattern Recognition and Machine Learning: A Matlab Companion. Springer, In preparation.
- 10. Mackay, D.J.C. (1988) Introduction to Gaussian Processes. In: Bishop, C.M., Ed., Neural Networks and Machine Learning, Springer.
- 11. Mackay, D.J.C. (2003) Information Theory, Inference and Learning Algorithms. Cambridge University Press, Cambridge.
- 12. Richard, J., Douglas, F. and Burden, L. (2005) Numerical Analysis. 9th Edition, Cengage Learning, Boston.
- 13. Robert, W.H. (1975) Numerical Analysis. Quantum Publishers, New York.
- 14. Bhatti, S. (2008) Analysis of the S. pombe Sister Chromatid Cohesin Subunit in Response to DNA Damage Agents During Mitosis. PhD Thesis, University of Glasgow.
http://theses.gla.ac.uk/292/ - 15. Wood, G. (1989) The Bisection Method in Higher Dimensions. Mathematical Programming, 55, 319-337.
- 16. Myung, I.J., Forster, M. and Browne, M.W. (2000) Special Issue on Model Selection. Journal of Mathematical Psychology, 44, 1-2.
- 17. Myung, I.J. (2003b) Tutorial on Maximum Likelihood Estimation. Journal of Mathematical Psychology, 47, 90-100.
http://dx.doi.org/10.1016/S0022-2496(02)00028-7 - 18. Berndt, E.K., Hall, B.H. and Hall, R.E. (1974) Estimation and Inference in Nonlinear Structural Models. Annals of Economic and Social Measurement, 3, 653-665.
- 19. Kloppers, P.H., Kikawa, C.R. and Shatalov, M.Y. (2012) A New Method for Least Squares Identification of Parameters of the Transcendental Equations. International Journal of the Physical Sciences, 7, 5218-5223.
http://dx.doi.org/10.5897/IJPS12.506 - 20. Krishnamoorthy, K. (2006) Handbook of Statistical Distributions with Applications. Chapman & Hall/CRC, London.
http://dx.doi.org/10.1201/9781420011371 - 21. Duda, R.O., Hart, P.E. and Stork, D.G. (1995) Pattern Classification and Scene analysis. John Wiley and Sons, New York.
- 22. Fayyad, U., Reina, C. and Bradley, P.S. (1998) Initialization of Iterative Refinement Clustering Algorithms. Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining (KDD98), New York, 27-31 August 1998, 194-198.
- 23. Kikawa, C.R., Shatalov, M.Y. and Kloppers, P.H. (2015) A Method for Computing Initial Approximations for a 3-Parameter Exponential Function. Physical Science International Journal, 6, 203-208.
http://dx.doi.org/10.9734/PSIJ/2015/16503 - 24. Pearson, K. and Lee, A. (1903) On the Laws of Inheritance in Man: Inheritance of Physical Characters. Biometrika, 2, 357-462.
http://dx.doi.org/10.1093/biomet/2.4.357 - 25. Sokal, R.R. and Hunter, P.E. (1955) A Morphometric Analysis of DDT-Resistant and Non-Resistant Housefly Strains. Annals of the Entomological Society of America, 48, 499-507.
http://dx.doi.org/10.1093/aesa/48.6.499 - 26. Hohle, J. (2009) Accuracy Assessment of Digital Elevation Models by Means of Robust Statistical Methods. Japan Society of Photogrammetry and Remote Sensing, 64, 398-406.
http://dx.doi.org/10.1016/j.isprsjprs.2009.02.003 - 27. Searl, R.S. (1971) Linear Models: John Wiley and Sons, Hoboken.
- 28. Kay, M.S. (1993) Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice-Hall, Upper Saddle River.
- 29. Muller, K.E. and Stewart, P.W. (2006) Linear Models Theory: Univariate, Multivariate, and Mixed Models. John Wiley and Sons, Hoboken.
http://dx.doi.org/10.1002/0470052147 - 30. NIST/SEMATECH (2012) e-Handbook of Statistical Methods.
http://www.itl.nist.gov/div898/handbook/ - 31. Burden, R.L. and Douglas, J.F. (2000) Numerical Analysis. 7th Edition, Brooks/Cole, Pacific Grove.
- 32. D’Agostino, R.B., Belanger, A., Ralph, B. and D’Agostino Jr., R.B. (1990) A Suggestion for Using Powerful and Informative Tests of Normality. The American Statistician, 44, 316-321.
NOTES
*Corresponding author.










