Received 5 February 2015; accepted 23 February 2015; published 26 February 2015

ABSTRACT

In this article, we consider a new life test scheme called a progressively first-failure censoring scheme introduced by Wu and Kus [1] . Based on this type of censoring, the maximum likelihood, approximate maximum likelihood and the least squares method estimators for the unknown parameters of the inverse Weibull distribution are derived. A comparison between these estimators is provided by using extensive simulation and two criteria, namely, absolute bias and mean squared error. It is concluded that the estimators based on the least squares method are superior compared to the maximum likelihood and the approximate maximum likelihood estimators. Real life data example is provided to illustrate our proposed estimators.

Keywords:

Inverse Weibull Distribution, Progressive First-Failure Censoring, Maximum Likelihood, Least Squares Method

1. Introduction

Let follow 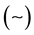a two-parameter Weibull distribution 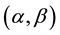with the probability density function (pdf)

then has an 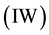distribution with pdf

(1)

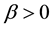where and, are the scale and shape parameters, respectively.

If, then the cumulative distribution function (cdf) of is given by:

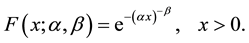(2)

The IW distribution, also known as type 2 extreme value or the Frechet distribution (Johnson et al. [2] ), has a long right tail compared to other known distributions. The hazard function of the IW distribution is similar to that of the log-normal and inverse gaussian distributions (Murthy et al. [3] ). Carriere [4] used the IW dis- tribution to model the mortality curve of a population. Keller and Kamath [5] suggested that this distribution was suitable to model the failure of the degradation phenomena of mechanical components of diesel engines such as pistons, crankshafts, and main bearings. Furthermore, Erto [6] showed that the IW distribution provided a good fit to several data such as the time to breakdown of an insulating fluid subjected to the action of a constant tension (Nelson [7] ).

Several researches have been carried out on the IW distribution using classical and Bayesian approaches. For example, Calabria and Pulcini [8] obtained the maximum likelihood estimates (MLE) and least squares esti- mates of the parameters of the IW distribution. Calabria and Pulcini [9] considered the Bayesian approach to predict the ordered lifetimes in a future sample when those lifetimes are assumed to follow the IW distribution. Panaitescu et al. [10] developed the Bayesian and non-Bayesian analysis in the context of recording statistic values from a modified IW distribution. All these studies have been done based on a complete sample. However, there are many scenarios in life testing and reliability experiment when researchers can not obtain complete information on failure times for all the units in the experiment as in the case of accidental breakage of an experimental unit or if an individual under study drops out. Moreover, there are many situations in which the researcher intentionally removes units prior to their failure and this is due to the lack of funds and/or time constrains. Data obtained from such experiments are called censored data. Therefore, we consider estimation procedures based on censored samples.

The most common censoring schemes are type-I censoring in which the test ceases at a pre-fixed time, and type-II censoring that allows the experiment to be terminated at a predetermined number of failures. These methods do not allow the removal of active units during the experiment; therefore, the focus in the last few years has been on progressive censoring due to its flexibility that allows the experimenter to remove active units during the experiment. A progressively type-II censoring is a generalization of type-II censoring. Many authors have discussed inference under progressive censoring using various lifetime distributions, among others, Cohen [11] , Mann [12] , Wingo [13] , Balakrishnan and Sandhu [14] , Aggarwala and Balakrishnan [15] , Balakrishnan and Asgharzadeh [16] . For a comprehensive recent review of progressive censoring, readers are referred to Balakrishnan [17] .

Johnson [18] introduced the first-failure censoring plan where the experimenter could arrange items into 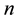sets, then all the 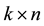items were tested simultaneously until the first failure in each 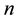set occurred. However, in situations where the lifetime of a product is high and test facilities are limited but test material is cheap. Balasooriya [19] modified Johnson [18] approach by testing each set one after the other until the first failure in each set occurred. This modified approach can save time and money.

However, due to certain situations such as loss of contact with the individuals under study or loss of experi- ment units as mentioned above, it is desirable for researchers to be able to remove sets before the final termina- tion point. This situation leads to the area of progressive censoring.

Wu and Kus [1] wanted to improve the efficiency of the test by developing a new life test scheme, pro- gressively first-failure censoring scheme, by combining the concept of first failure censoring with the pro- gressive censoring. In this scheme sets with no failures can be removed from the test before the end of the experiment. Based on this scheme, Wu and Kus [1] derived the MLEs and constructed exact and approximate confidence intervals for the parameters of the Weibull distribution. Wu and Huang [20] developed the reliability sampling plans for the Weibull distribution. Soliman et al. ( [21] [22] ) derived Bayes and frequentist estimators for the parameters of Gompertz and Burr type XII distributions respectively. Hong et al. [23] used the same

scheme to construct MLE for the lifetime performance index C_L based on progressively first-failure censoring from Weibull distribution. Ahmadi et al. [24] developed a confidence interval and ML estimator for C_L based on the progressive first-failure censored sample under the Weibull distribution when the shape parameter was known.

In this study and based on m progressively first-failure censored sample from IW model, we consider the problem of estimating the parameters of the model using the maximum likelihood, the approximate maximum likelihood and the least square estimators (LSE). Balakrishnan et al. [25] conducted inference on progressive type-II censored data for extreme value distribution. They derived the MLE and approximate values for the maximum likelihood estimators (AMLE) using the Taylor expansion. They also concluded that the MLEs and AMLEs were almost identical in terms of bias and variance. Kim et al. [26] derived the maximum likelihood and the Bayes estimates for the three-parameter exponentiated Weibull distribution for type-II progressively censored sample. Gusmao et al. [27] studied the properties of a mixture of two generalized IW distribution and derived the maximum likelihood estimator of the parameters of this mixture based on censored data.

This article unfolds as follows: In Section 2 we describe the formulation of a progressive first-failure cen- soring scheme as described by Wu and Kus [1] . The MLEs, approximate MLEs, and LSE methods for estimat- ing the unknown parameters based on the progressive first-failure censoring scheme are derived in Section 3, 4 and 5 respectively. Simulation studies, results and conclusion are presented in Section 6. All methods that are discussed in this article are illustrated in Section 7 through a real life data set coming from highways pavement projects in Amman-Jordan during 2012.

2. A Progressive First-Failure Censoring Scheme

The progressive first-failure censoring can be described as follows: Given and non-

negative integers such that. Let n independent groups with items within each group be placed

on a life testing experiment and only failures are completely observed. The censoring occurs progressively in stages. At the time of the first failure, random groups and the group with the observed failure are randomly removed. Similarly, at the time of the second failure, random groups and the group with the observed failure are randomly removed and so on. Finally, at the time of the -th failure all the remaining active groups and the group with the observed failure are removed. Then is the progressive first-failure censored order statistics.

The main advantage of this scheme is that it reduces the time in which more items are used but only m out of items are observed. Moreover, it includes as special cases, the progressively type-II scheme (when k = 1), first-failure scheme (when), conventional type II scheme (when k = 1 and and the complete sample (when and). Furthermore, the progressively first- failure censored sample can be considered as a progressively type-II censored

sample from a population with distribution function (Wu and Kus [1] ) which enables us to

extend all the results on progressively type-II censored order statistics to progressively first-failure censored order statistics.

3. Maximum Likelihood Estimation

Suppose that independent units are placed on a test. The ordered failures are observed under the progressively first-failure.

Let with denote the progressively first-failure cen- sored ordered statistics with the progressive censoring scheme from a population with pdf and cdf given in Equations (1) and (2), respectively. For notation simplicity, we will write for. The likelihood func- tion based on progressively first-failure censored sample (see Wu and Kus [1] ) is given by:

(3)

where,

In accordance with (1), (2) and (3), the log-likelihood function of and based on progressively first- failure censored sample becomes

(4)

The MLEs of the parameters and can be obtained by deriving (4) with respect to and and equating the normal equations to 0 as follows:

(5)

(6)

The MLEs are exist and unique (see Calabria and Pulcini [8] and Marusic et al. [28] ). Notice that there are no explicit solutions to (5) and (6). Hence, numerical methods are applied to solve the required equations. The maximum likelihood estimation method based on progressively censored data has been studied extensively, but traditionally, the Newton Raphson (NR) method was utilized to obtain the MLEs (Ng et al. [29] ). However, the MLEs via the NR method are very sensitive to their initial parameters estimation value. In this article we propose using the Expectation-Maximization (EM) algorithm for computing the MLEs.

4. Approximate Maximum Likelihood Estimation

Since the MLE does not provide explicit estimators for the shape and scale parameters of the IW distribution as mentioned before, we derive approximate MLE (AMLE) for the parameters and.

Balakrishnan ( [30] - [34] ) and Balakrishnan and Vardan [35] developed the AMLE procedure. This procedure depends on the Taylor expansion of the likelihood function when the pdf under consideration belongs to the location-scale families. However, the IW distribution does not have the location-scale structure required for the AMLE procedure, but if we consider the transformation, then extreme value distribution and this distribution has this feature.

The and of are given respectively by

(7)

and,

(8)

where, and are the location and scale parameters respectively.

Hence, the AMLE procedure can be used to estimate the parameters and of the IW distribution.

Let with denotes a progressively first-failure censored sample from (7) and (8). Then the joint pdf based on the censored sample is given by:

(9)

where,

If, then (9) can be written as

(10)

with log-likelihood equation

(11)

Taking derivatives with respect to and and equating them to zero, gives

(12)

(13)

Because of the presence of the terms and, Equations (12) and (13) do not have explicit solution. Hence, we consider a first-order Taylor approximation to and around

(see Balakrishnan and Aggarwala [36] ; for reasoning).

From Balakrishnan and Aggarwala [36] , if denote a progressively first-failure censored

sample from Uniform with censoring scheme, then, are statistically independent random variables from Beta with

(14)

and,

(15)

The approximation is around upon expanding and around the point and keeping only the first two terms, we get

(16)

where,

and,

(17)

where,

Plugging (16) and (17) in (12) and (13) we get

(18)

and,

(19)

where,. Equations (18) and (19) can be rewritten as

(20)

(21)

where,

The solutions to (20) and (21) yield the AMLEs

(22)

One of the drawbacks of the AMLEs is that they are biased. Moreover, the exact bias of and can not be theoretically computed because of the intractability encountered of. On the other hand, the AMLEs provide an excellent starting value for the iterative solution of the likelihood equations.

5. Least Squares Estimation Method

The LS method which is originally suggested by Swain et al. [37] is computationally easier to handle, it provides simple closed form solutions for estimates (Hossain and Zimmer [38] ). In addition it can also be used quite effectively to estimate the shape and scale parameters of the IW distribution. Finally Marusic et al. [28] showed that the least squares estimators (LSE) for estimating the parameters of the IW distribution did exist.

In this section we will discuss the least squares method for estimating and using the set up in Section 1; that is, are progressively first-failure censored sample from the IW distribution with censoring scheme. The LS method is a combination of parametric and non-parametric distribution functions. It depends on the choice of which should be as effective as possible. In our study we use which is proposed by Montanari and Cacciari [39] as a non-parametric for progressive type-II censored sample.

(23)

where,

and,

For the parametric cdf, Balakrishnan and Aggarwala [36] and Kim and Han [40] , proposed

(24)

where,

The procedure attempts to minimize the following function with respect to and

(25)

The LSE estimates of and are denoted by and respectively.

6. Simulation Study

The purpose of the simulation study is to compare the performance of the MLE, AMLE and LSE estimates based on progressively first-failure censored samples generated from the IW distribution with , , , , , , using different combinations of and different censoring schemes. The data are simulated using Balakrishnan and Aggarwala [36] algorithm based on the fact that progressively first-failure censored sample with distribution can be

viewed as a progressively type II censored sample from a population with distribution function.

We obtain the MLEs of and by solving the nonlinear Equations (5) and (6), in which the AMLEs are used as starting values of the MLE iterations. The AMLE and LSE are computed using (22) and (25) respec- tively. The criteria used for comparing all the above estimates are the absolute bias (ABias) and the mean squared error (MSE). Suppose is the estimate of for the i-th simulated data set, then the ABias and MSE are computed as follows:

1).

2).

6.1. Data Analysis and Comparison Study

Due to the large number of tables, only part of them is reported. Results are summarized in Tables 1-4 provided at the end of this section as follows:

・ Table 1 and Table 2 provide the ABias and MSE values for the estimates of.

・ Table 3 and Table 4 provide the ABias and MSE values for the estimates of.

Throughout this section we will refer to by, by

(where), by, by,

by, and finally by. Moreover, we will refer to schemes, , and by group-1, similarly we will refer to the schemes, , and by group-2. A summary of the results is provided below.

6.1.1. Scale Parameter

・ For progressively first-failure censoring we can easily notice that is the most efficient

scheme in terms of ABias and MSE values for MLE and AMLE, while scheme is the most efficient

scheme for LSE. On the other hand when, that is the progressively type-II censoring, scheme is the most efficient for all estimates namely MLE, AMLE and LSE.

・ Notice that when is small, the MSE values are almost identical for all the estimates regardless of the different schemes and the different values of, this indicates that the estimates of are sensitive to the choice of.

・ In general, LSE and MLE have comparable ABias and MSE values, which makes LSE estimates very good competitors to the MLE estimates.

6.1.2. Shape Parameter

・ When scheme is the most efficient scheme in terms of ABias and MSE values for MLE and LSE.

・ For progressively type-II censoring scheme is the most efficient in terms of ABias and MSE values for MLE while scheme is the most efficient for LSE.

・ As for the AMLE estimates, we notice that the scheme is the most efficient in terms of ABias whereas

scheme is the most efficient in terms of MSE values for all values of.

・ In addition, generally has the smallest ABias while has the smallest MSE values.

6.2. Conclusions and Recommendations

In the past few years, progressive censoring has received a great attention by many researchers. This is due to its advantages in reducing the cost and time of the tests. Moreover, the availability of high speed computing re- sources enhances the focus on progressive censoring. In this article, we have considered the MLE, approximate MLE and LSE to estimate the unknown parameters of the IW distribution when data under consideration are progressively first-failure censoring.

It is out of question that all estimates are affected by the choice of, and our goal is to compare the three methods namely MLE, AMLE and LSE and decide which is the most efficient for estimating and. It is important to point out the following:

・ The results for group-1 and group-2 are very similar with slight edge improvement in favor of group-1.

・ ABias and MSE values decrease as the effective sample proportion increases for fixed and for all estimates of and.

・ In general, progressively first-failure censoring (i.e.) is more efficient compared to progressive type-II censoring in terms of ABias and MSE values. This is true for MLE and LSE estimates.

・ Table 1 and Table 2 clearly show that the MSE values for LSE and MLE are almost identical and their ABias is comparable. Moreover, Table 3 and Table 4 show the similarity in performance between LSE and MLE for estimating. Keep in mind that LSE formula is simple and easy to implement compared to the formula of the MLE.

Based on this, we highly recommend using LSE method and progressively first-failure censoring scheme for estimating the parameters of the IW distribution.

7. Real Life Data

In this example, we consider a real life data set to illustrate the proposed method and verify how our estimators work in practice. The validity of the IW model is checked using Kolmogrov-Smirnov test, as well as Anderson-Darling and chi-square tests. The data set for this application came from a real highway construction project in Amman/Jordan supervised by the Greater Amman Municipality and executed by a local contractor in 2012 (http://www.ammancity.gov.jo/en/gam/index.asp). The data consist of 64 readings that de- monstrate the percentage of asphalt content in hot mix asphalt specimens sampled from the mentioned project above. Percentage of asphalt content is one of the main elements of a hot mix asphalt sample characteristics that has a direct effect on the quality and durability of the pavement. That is why this data is used in this example.

We fit the IW distribution based on and. We observe that with, and chi-square distance = 0.6468 with a corresponding. This indicates that the IW model provides a good fit. The initial estimates for the MLEs are chosen by using pseudo complete estimates of the MLEs. We group the data into 32 sets with 2 items in each. We modify the data to consider four types of censoring as follows:

The modified data sets are provided in Table 5. The evaluated Hessian matrix to guarantee the uniqueness of the MLEs is presented in Table 6. Finally, the estimates of and based on different estimation methods are provided in Table 7.

It is quite clear that all the estimates for the scale parameter are quite close to each other. It is of great importance to notice through this analysis that the estimates based on progressively first-failure are comparable with the values of the estimates based on progressively type-II censored samples and they are very close to those of the complete data set. Although is higher than and, it is however comparable with its value when data is complete. Moreover, in this case is the closest to the complete case.

Cite this paper

AmalHelu, (2015) On the Maximum Likelihood and Least Squares Estimation for the Inverse Weibull Parameters with Progressively First-Failure Censoring. Open Journal of Statistics,05,75-89. doi: 10.4236/ojs.2015.51010

References