Open Journal of Statistics
Vol.2 No.1(2012), Article ID:16878,8 pages DOI:10.4236/ojs.2012.21010
On the Spectrum of Asymptotic Expansions for an Asymptotic Normal Sequence
Department of Mathematics and Statistics, University of Victoria, Victoria, Canada
Email: tsao@math.uvic.ca
Received September 20, 2011; revised October 18, 2011; accepted October 29, 2011
Keywords: Asymptotic Expansion; Asymptotic Normal Sequence; Edgeworth Expansion; Saddlepoint Expansion; Saddlepoints Expansion; Hermite Polynomials
ABSTRACT
We present a family of formal expansions for the density function of a general one-dimensional asymptotic normal sequence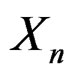 . Members of the family are indexed by a parameter
. Members of the family are indexed by a parameter 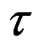 with an interval domain which we refer to as the spectrum of the family. The spectrum provides a unified view of known expansions for the density of
with an interval domain which we refer to as the spectrum of the family. The spectrum provides a unified view of known expansions for the density of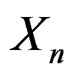 . It also provides a means to explore for new expansions. We discuss such applications of the spectrum through that of a sample mean and a standardized mean. We also discuss a related expansion for the cumulative distribution function of
. It also provides a means to explore for new expansions. We discuss such applications of the spectrum through that of a sample mean and a standardized mean. We also discuss a related expansion for the cumulative distribution function of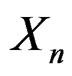 .
.
1. Introduction
Historically, formal expansions (i.e., non-rigorous expansions) for distributions of random variables have played an important role in the development of asymptotic theories in statistics. The most well-known example is the Edgeworth expansion for the density of a standardized mean which was first derived in 1905 as a formal expansion for the density [1]. The method used by Edgeworth in his derivation made use of Charlier differential series and a standard normal density as a developing function [2]. This method did not address the validity of the expansion, but the expansion was proven valid by Cramér 23 years later in [3,4]. See also [5]. Another well-known example is that of the formal expansion by Wallace [2]. Its validity was given 20 years later in [6]. Indeed, formal expansions often serve as the first step in exploring valid expansions for random variables. Furthermore, they may be valuable approximation tools even in the absence of a rigorous treatment of their validity. There are many useful formal approximations that are numerically very accurate. For more recent examples, see [7,8].
Nevertheless, in spite of the usefulness of formal expansion there does not seem to exist a systematic approach for deriving such expansions in the literature. To obtain an Edgeworth type of expansion for an asymptotically normal sequence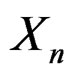 , the common approach is to use the moments of
, the common approach is to use the moments of  (or in the absence of the exact moments, the approximate moments obtained through the delta method) and substitute them into the Edgeworth expansion formula for the standardized mean. To obtain a saddlepoint type of expansion, one often follows Daniels’s derivation [9] of the expansion for a sample mean by writing the cumulant generating function (or an approximation to the cumulant generating function) as a product of the sample size
(or in the absence of the exact moments, the approximate moments obtained through the delta method) and substitute them into the Edgeworth expansion formula for the standardized mean. To obtain a saddlepoint type of expansion, one often follows Daniels’s derivation [9] of the expansion for a sample mean by writing the cumulant generating function (or an approximation to the cumulant generating function) as a product of the sample size 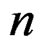 and another function, say
and another function, say . Then applying the method of steepest descent to an inversion formula as if
. Then applying the method of steepest descent to an inversion formula as if  is independent of the asymptotic factor
is independent of the asymptotic factor . See, for example, [10,11]. Such methods work on the particular cases in question but offer little insight into how a formal expansion should be sought in general.
. See, for example, [10,11]. Such methods work on the particular cases in question but offer little insight into how a formal expansion should be sought in general.
The main purpose of this paper is to introduce a family of formal expansions for a general asymptotic normal sequence . Members of the family are indexed by a parameter
. Members of the family are indexed by a parameter  with an interval domain which we call the spectrum of the expansions. The spectrum has the following applications. 1) It provides a means to study the whole family of formal expansions and search for good and valid expansions. 2) It provides a way to view known expansions from a unified standpoint, thereby linking seemingly unrelated expansions under a unified framework. For the case of a standardized mean, for example, the Edgeworth expansion and the saddlepoints expansion [12] are actually members of the same family, although they are based on different asymptotic sequences and are substantially different in structure. 3) Existing expansions are mostly power sequence expansions in that individual terms of the expansions are of the form
with an interval domain which we call the spectrum of the expansions. The spectrum has the following applications. 1) It provides a means to study the whole family of formal expansions and search for good and valid expansions. 2) It provides a way to view known expansions from a unified standpoint, thereby linking seemingly unrelated expansions under a unified framework. For the case of a standardized mean, for example, the Edgeworth expansion and the saddlepoints expansion [12] are actually members of the same family, although they are based on different asymptotic sequences and are substantially different in structure. 3) Existing expansions are mostly power sequence expansions in that individual terms of the expansions are of the form 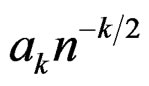 or
or . The spectrum contains “non-standard” expansions which are not power sequence expansions. This allows one to explore new expansions which are not power sequence expansions. In cases where
. The spectrum contains “non-standard” expansions which are not power sequence expansions. This allows one to explore new expansions which are not power sequence expansions. In cases where  is neither the mean nor the standardized mean of iid observations, such “non-standard” expansions may be more natural expansions than those based on the power sequences
is neither the mean nor the standardized mean of iid observations, such “non-standard” expansions may be more natural expansions than those based on the power sequences  or
or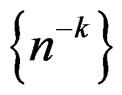 .
.
The rest of this paper is organized as follows: in Section 2, we derive the family of formal expansions. In Section 3, we discuss the validity of the family for the cases of the sample mean and the standardized mean. For the latter case, the family led to a set of valid new expansions for the density function. In Section 4, we consider a related formal expansion for the distribution function. Concluding remarks in Section 5 will include further notes on previous work which have motivated this paper.
2. The Family of Formal Expansions
Suppose 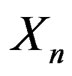
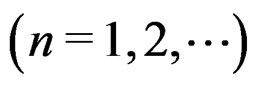 has a density function
has a density function 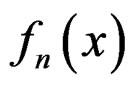 and a moment generating function
and a moment generating function . Assume that as
. Assume that as 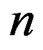 approaches infinity the interval in which
approaches infinity the interval in which 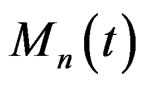 exists approaches a non-vanishing open interval
exists approaches a non-vanishing open interval  where
where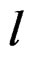 ,
,  are constants and
are constants and . We will derive a formal expansion for
. We will derive a formal expansion for  at each point
at each point 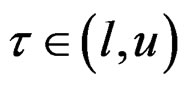 and thus we call
and thus we call  the spectrum of the formal expansions for
the spectrum of the formal expansions for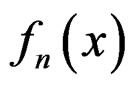 . To derive the formal expansion at a point
. To derive the formal expansion at a point , we need the following inversion formula
, we need the following inversion formula
 (1)
(1)
where ,
, 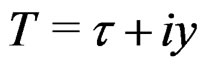 and
and . A key result that will be used in the derivation is the following lemma which establishes a new defining relation for Hermite polynomials.
. A key result that will be used in the derivation is the following lemma which establishes a new defining relation for Hermite polynomials.
Lemma 1: Let 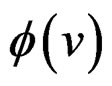 be the density function of the standard normal distribution and
be the density function of the standard normal distribution and  be the Hermite polynomial of degree
be the Hermite polynomial of degree . Then
. Then
 (2)
(2)
for 
Proof of Lemma 1: See Appendix.
The derivation of the formal expansion at  involves the following two steps. Step 1: obtaining a formal series representation of the density function, and Step 2: rearranging terms in the formal series representation according to their asymptotic orders. Step 1 is achieved by first replacing the exponent of the integrand in (1) with its Taylor series expansion, then isolating the quadratic term of the Taylor series and performing a term-by-term integration. Note that in this step no attempt will be made to isolate the asymptotic factor
involves the following two steps. Step 1: obtaining a formal series representation of the density function, and Step 2: rearranging terms in the formal series representation according to their asymptotic orders. Step 1 is achieved by first replacing the exponent of the integrand in (1) with its Taylor series expansion, then isolating the quadratic term of the Taylor series and performing a term-by-term integration. Note that in this step no attempt will be made to isolate the asymptotic factor 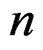 from the exponent since we do not presume that the expansion of interest is based on a power sequence of
from the exponent since we do not presume that the expansion of interest is based on a power sequence of . Also, with the aid of Lemma 1, Step 1 is independent of
. Also, with the aid of Lemma 1, Step 1 is independent of  and gives a unified series representation for all
and gives a unified series representation for all 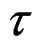 values in the spectrum as we will see in the proof of Theorem 1 below.
values in the spectrum as we will see in the proof of Theorem 1 below.
Theorem 1: For any  where
where ,
,  has the following formal series representation (3)
has the following formal series representation (3)
where  is the density function of the normal distribution with mean
is the density function of the normal distribution with mean  and variance
and variance
 , and
, and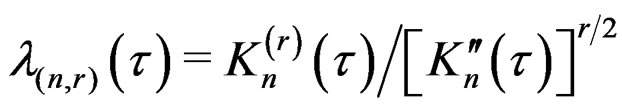 .
.
Proof of Theorem 1: For convenience of presentation, we first consider the special case of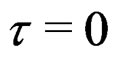 . By setting
. By setting  in (1) to
in (1) to , on the path of integration near the origin we have
, on the path of integration near the origin we have
 (4)
(4)
Since 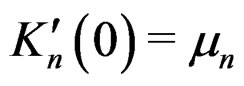 and
and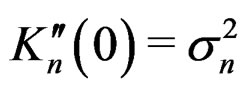 , where
, where  and
and 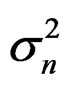 are the mean and variance of
are the mean and variance of , (4) may be written as
, (4) may be written as
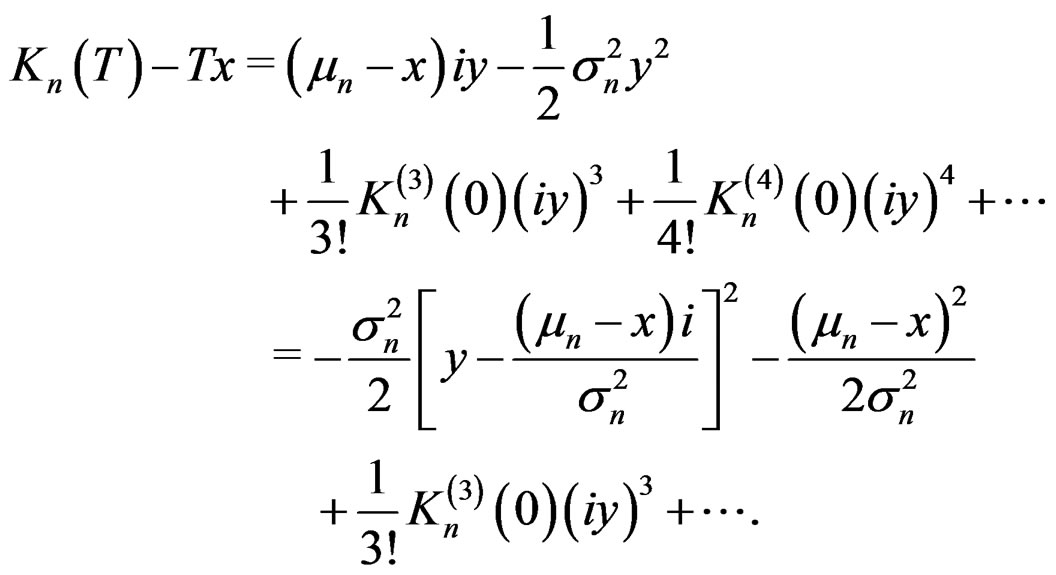 (5)
(5)
Letting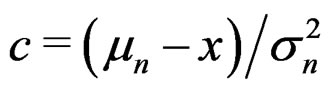 , Equation (1) may be formally rewritten as
, Equation (1) may be formally rewritten as
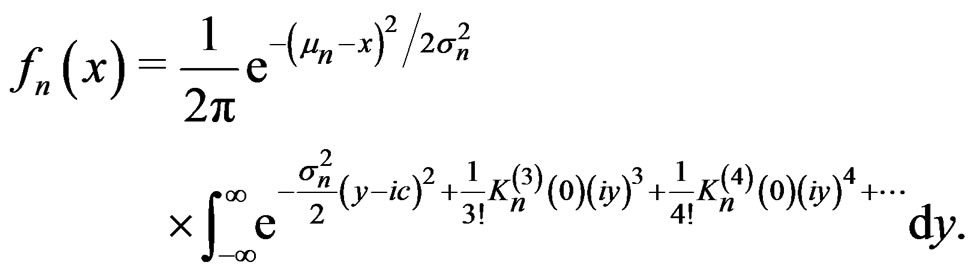 (6)
(6)
 (3)
(3)
Letting  and
and  for
for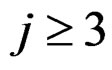 , we may write (6) as
, we may write (6) as
 (7)
(7)
where  is the density of
is the density of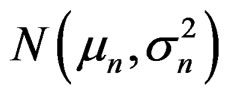 , and for brevity we have written
, and for brevity we have written  as
as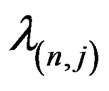 . Expanding the function
. Expanding the function  in the integrand, we get
in the integrand, we get
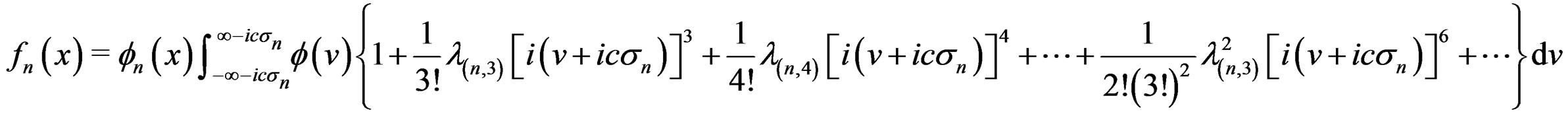
(8)
We now perform the term-by-term integration for the right-hand side of (8). This is easily carried out using Lemma 1 by noting that  is an entire function. Thus the contour of integration in (8) may be deformed from
is an entire function. Thus the contour of integration in (8) may be deformed from 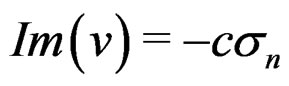 to
to . This and Lemma 1 lead to
. This and Lemma 1 lead to
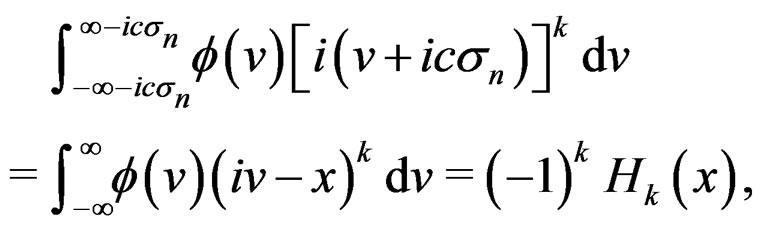 (9)
(9)
for . It follows that
. It follows that
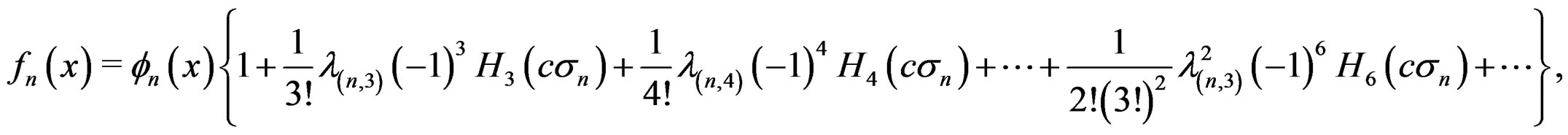 (10)
(10)
or equivalently
 (11)
(11)
which is the formal series representation (3) at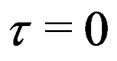 .
.
For a general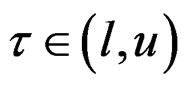 ,
, 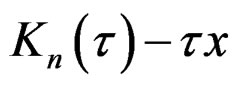 may not be zero and (4) becomes
may not be zero and (4) becomes
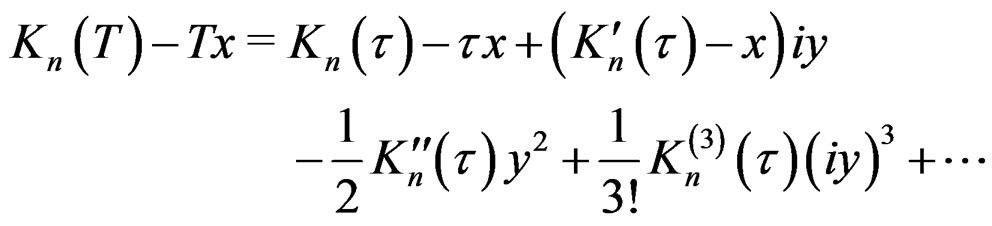 (12)
(12)
Let 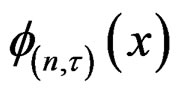 be the density function of the normal distribution with mean
be the density function of the normal distribution with mean 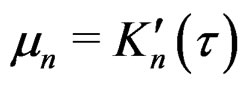 and variance
and variance 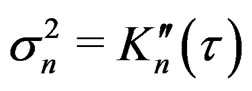 and write
and write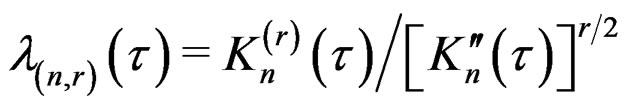 . By replacing (4) with (12) and then following the same steps for the case of
. By replacing (4) with (12) and then following the same steps for the case of  shown above, we obtain (3).
shown above, we obtain (3). 
The series representation (3) takes on a simpler form (11) for the special case of  because the
because the 
term in (3) is not in (11). Another special case where (3) has a simpler form is the case where 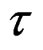 is the saddlepoint
is the saddlepoint  satisfying
satisfying . Define
. Define , the generalized saddlepoint approximation for
, the generalized saddlepoint approximation for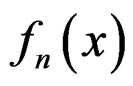 , as
, as
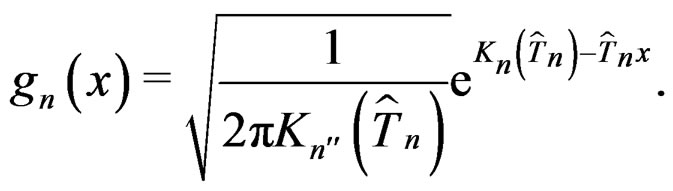 (13)
(13)
Setting  to
to  in (3) and noting that
in (3) and noting that  , we obtain the series representation of
, we obtain the series representation of 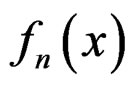 at the saddlepoint:
at the saddlepoint:
 (14)
(14)
Note that here  depends on
depends on  and thus is not a constant in the spectrum as
and thus is not a constant in the spectrum as  changes.
changes.
We now discuss Step 2. Series (3), (11) or (14) are not particularly useful from an asymptotic expansion point of view in that they, like Charlier differential series, do not use information concerning the asymptotic properties of the distribution of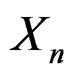 . They are not asymptotic expansions for
. They are not asymptotic expansions for . When
. When 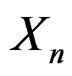 is asymptotically normal, the sequence
is asymptotically normal, the sequence 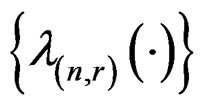 may be an asymptotic sequence and may thus be used to transform these series into formal asymptotic expansions. To do so, we need to rearrange terms in the curly brackets in (3), (11) and (14) in ascending order according to the rates at which the
may be an asymptotic sequence and may thus be used to transform these series into formal asymptotic expansions. To do so, we need to rearrange terms in the curly brackets in (3), (11) and (14) in ascending order according to the rates at which the ’s approach zero. Corollary 1 below gives the rearranged series at the saddlepoint (14).
’s approach zero. Corollary 1 below gives the rearranged series at the saddlepoint (14).
Corollary 1: Suppose 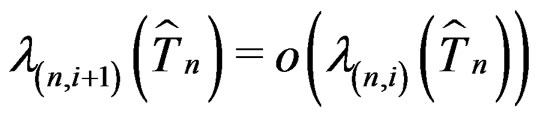 as
as 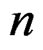 approaches infinity for
approaches infinity for 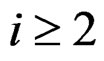 and in particular
and in particular . Then we have formally
. Then we have formally
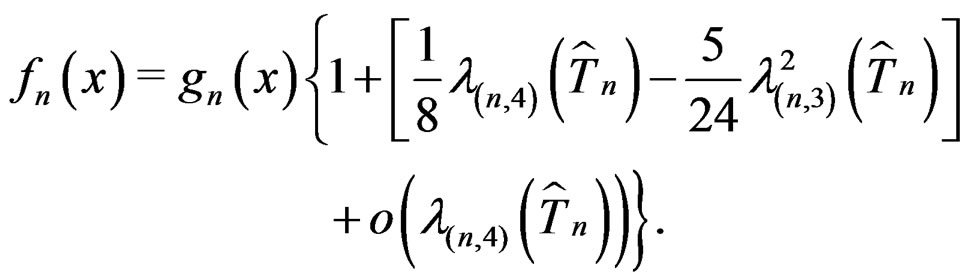 (15)
(15)
We refer to (15) this as the generalized saddlepoint expansion for  based on the asymptotic sequence
based on the asymptotic sequence
 . Note that conditions in Corollary 1 are satisfied by a large class of statistics
. Note that conditions in Corollary 1 are satisfied by a large class of statistics , including the sample mean.
, including the sample mean.
To transform the general series (3) into a formal expansion, we also need to consider the Hermite polynomials that appear in (3). If the absolute value of their common argument,  , goes to infinity when
, goes to infinity when 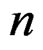
goes to infinity, then since  is a polynomial of order
is a polynomial of order . The reciprocals of these polynomials
. The reciprocals of these polynomials 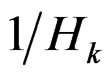
 will form an asymptotic sequence with respect to
will form an asymptotic sequence with respect to . Thus (3) contains ratios of terms in two asymptotic sequences
. Thus (3) contains ratios of terms in two asymptotic sequences 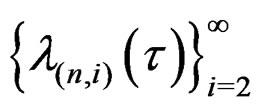 and
and and its asymptotic properties become complicated. To avoid this complication, we assume that
and its asymptotic properties become complicated. To avoid this complication, we assume that  is bounded. With this assumption, the relative rate at which terms in the curly bracket of (3), such as
is bounded. With this assumption, the relative rate at which terms in the curly bracket of (3), such as  and
and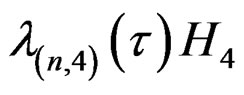 , approach zero is determined by that of the
, approach zero is determined by that of the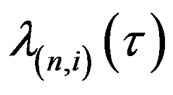 ’s. Rearranging terms in (3), we have Corollary 2: Suppose
’s. Rearranging terms in (3), we have Corollary 2: Suppose  for
for 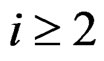 and
and  is bounded as
is bounded as 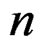 approaches infinity. Then we have formally (16) where
approaches infinity. Then we have formally (16) where  and
and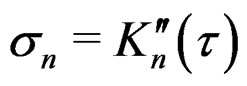 .
.
In particular, at  formal expansion (16) becomes (17).
formal expansion (16) becomes (17).
We refer to (16) as the general expansion for 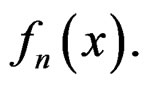 and (17) as the generalized Edgeworth expansion because the latter is the expansion at the origin but unlike the Edgeworth expansion which is based on the power sequence
and (17) as the generalized Edgeworth expansion because the latter is the expansion at the origin but unlike the Edgeworth expansion which is based on the power sequence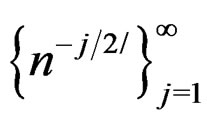 , (17) is based on a general asymptotic sequence
, (17) is based on a general asymptotic sequence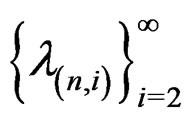 .
.
Note that conditions on the relative order of the
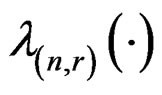 ’s and the boundedness of
’s and the boundedness of 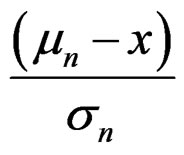 in the corollaries are easily verified once
in the corollaries are easily verified once  is given. When some of these conditions are not met, terms in the series representations need to be arranged accordingly. The resulting formal expansions may be different from those obtained above but the leading term should still be
is given. When some of these conditions are not met, terms in the series representations need to be arranged accordingly. The resulting formal expansions may be different from those obtained above but the leading term should still be
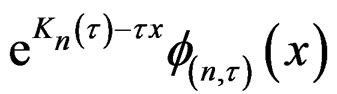 .
.
3. The Spectrum of the Sample Mean and Standardized Mean
To demonstrate the use of the spectrum, we now examine the spectrum for the important cases of sample mean and standardized mean. We show that the known expansions such as the saddlepoint, Edgeworth and saddlepoints expansions, can all be located through the spectrum. Moreover, we examine the validity of other expansions in the spectrum.
3.1. Expansions for the Density of the Sample Mean
Let 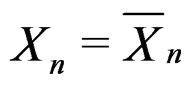 be the average of
be the average of  independent copies of a random variable
independent copies of a random variable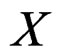 . How does the generalized saddlepoint expansion relate to the saddlepoint expansion for
. How does the generalized saddlepoint expansion relate to the saddlepoint expansion for 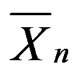 given by Daniels [9]? Let
given by Daniels [9]? Let 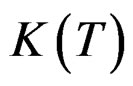 be the cumulant generating function of
be the cumulant generating function of , then
, then . Let
. Let 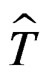 be the solution of
be the solution of , then
, then . Furthermore,
. Furthermore, 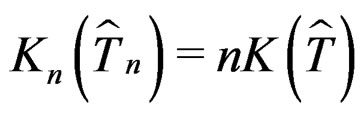 and
and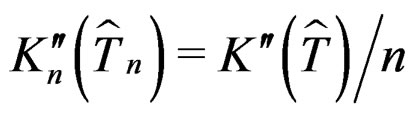 .
.
Thus the generalized saddlepoint approximation (13) is the same as Daniels’s saddlepoint approximation,
 .
.
To examine the asymptotic property of other terms of the generalized saddlepoint expansion (15), we first note that  for any
for any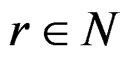 . Hence
. Hence 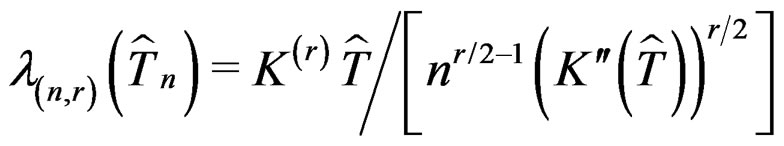 for
for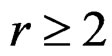 . Denote
. Denote 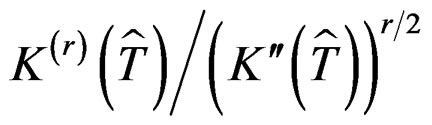 by
by . It is not difficult to show that
. It is not difficult to show that

which is  in the saddlepoint expansion in [9]. Further
in the saddlepoint expansion in [9]. Further
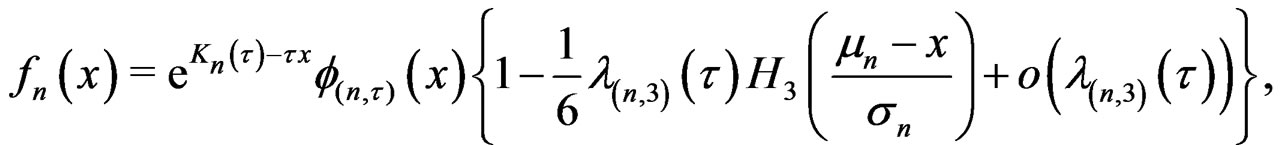 (16)
(16)
 (17)
(17)
terms in expansion (15) may be constructed for this particular case and it can be shown that they are equal to the corresponding terms in Daniels’s saddlepoint expansion. Thus the generalized saddlepoint expansion (15) is Daniels’s saddlepoint expansion.
It may also be easily verified using the same arguments demonstrated above that the general expansion (16) coincides with the expansion Daniels derived through the Edgeworth expansion at 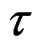 in [9]. See (4.3) in Section 4 in Daniels (1954). We will refer to this (4.3) as D(4.3). Daniels [9] stated that the family of expansions given by D(4.3) are asymptotic expansions for
in [9]. See (4.3) in Section 4 in Daniels (1954). We will refer to this (4.3) as D(4.3). Daniels [9] stated that the family of expansions given by D(4.3) are asymptotic expansions for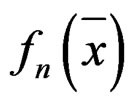 . This, however, is not accurate. The reason is that the Edgeworth expansion for a standardized variable
. This, however, is not accurate. The reason is that the Edgeworth expansion for a standardized variable  may not be used to obtain an asymptotic expansion for the density of
may not be used to obtain an asymptotic expansion for the density of 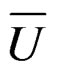 at anywhere except for
at anywhere except for . The distribution of the random variable
. The distribution of the random variable  described before D(4.3) has mean
described before D(4.3) has mean  , but D(4.3) was derived through the Edgeworth expansion for
, but D(4.3) was derived through the Edgeworth expansion for 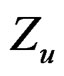 at
at 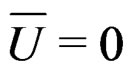 or
or
 . Thus when
. Thus when
 , expansions given by D(4.3) are not valid.
, expansions given by D(4.3) are not valid.
More specifically, the coefficient  in D(4.3), for example, is in general
in D(4.3), for example, is in general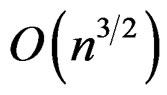 . Thus the second term in D(4.3),
. Thus the second term in D(4.3), 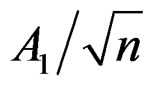 , is in general
, is in general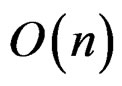 . Hence D(4.3) cannot even be an asymptotic expansion in a formal sense. This illustrates the necessity of the condition that
. Hence D(4.3) cannot even be an asymptotic expansion in a formal sense. This illustrates the necessity of the condition that 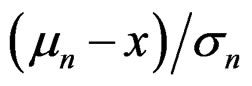 be bounded, which we have used in arriveing at (16).
be bounded, which we have used in arriveing at (16).
3.2. Expansions for the Density of the Standardized Mean
It is not difficult to verify that for this case the generalized Edgeworth expansion (17) coincides with the Edgeworth expansion. Furthermore, the saddlepoints approximation for the density of a standardized mean given by Routledge and Tsao [12] is actually the generalized saddlepoint expansion (15). We now focus on the validity of a set of new expansions within the family. These correspond to members of the family at other points of the spectrum. By (16), these have the expression
 (18)
(18)
Although in this case the 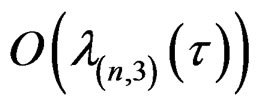 term in (18) and the
term in (18) and the  term in (16) may be easily further expanded, verification of the validity of expansions with more terms than that in (18) is more involved and will not be considered here. We only consider (18) for which the validity of the family can be established. The following equation will be used implicitly for showing the validity:
term in (16) may be easily further expanded, verification of the validity of expansions with more terms than that in (18) is more involved and will not be considered here. We only consider (18) for which the validity of the family can be established. The following equation will be used implicitly for showing the validity:
 (19)
(19)
where  and
and .
.
Let  be the cumulant generating function of the standardized mean. Then its derivatives have the following expansions: (i)
be the cumulant generating function of the standardized mean. Then its derivatives have the following expansions: (i) , (ii)
, (ii)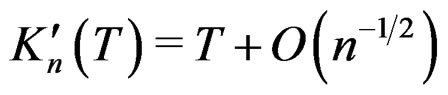 , (iii)
, (iii) , and iv)
, and iv)  for
for . Denote the leading term of the expansion in (18) by
. Denote the leading term of the expansion in (18) by . We have
. We have

Equations (i), (ii), (iii) and (19) imply that
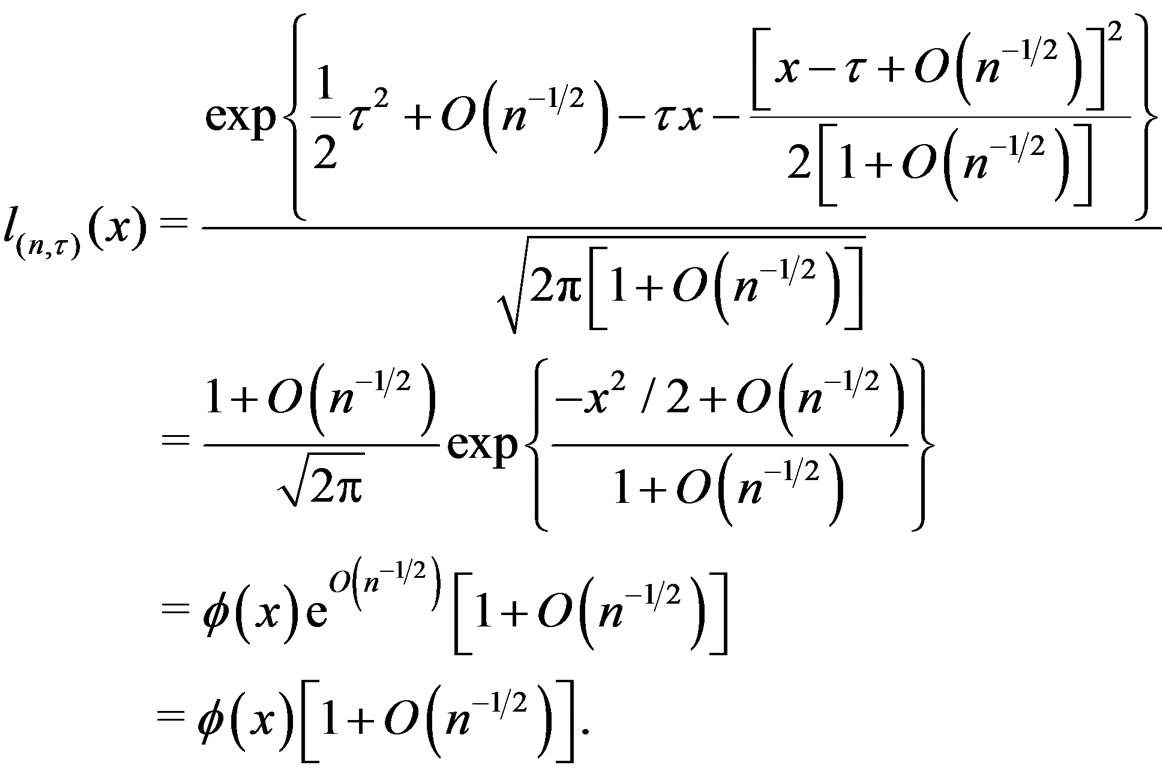
(20)
Also, (iii) and (iv) imply that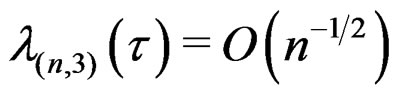 . Thus (20) may be written as
. Thus (20) may be written as
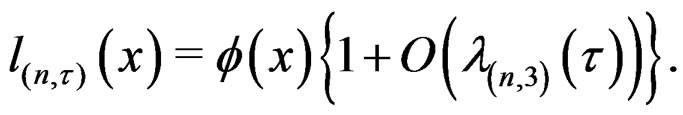
By the Edgeworth expansion,
 . Thus
. Thus
 (22)
(22)
This proves the validity of (18). We have compared the numerical accuracy of 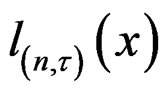 to the normal approximation
to the normal approximation  for small and moderately large sample sizes through a number of examples. Not surprisingly,
for small and moderately large sample sizes through a number of examples. Not surprisingly, 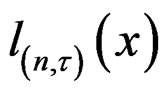 is substantially more accurate than
is substantially more accurate than  when
when  is close to the saddlepoint. They are about the same when
is close to the saddlepoint. They are about the same when 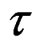 is near zero.
is near zero.
To summarize, all known expansions for the above two special cases have been located in their spectrums. For the sample mean, the generalized saddlepoint expansion is the only member which is a valid asymptotic expansion. For the standardized mean, new valid expansions have been found.
4. Expansions for the Distribution Function
The formal expansions for density functions may be integrated to obtain expansions for the corresponding distribution function, . Consider the case where
. Consider the case where  and
and . By formally integrating (17), we obtain the generalized Edgeworth expansion
. By formally integrating (17), we obtain the generalized Edgeworth expansion
 (23)
(23)
It may be easily verified that (23) is the same as the Edgeworth expansion for the distribution function when 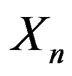 is the standardized mean. We now consider another example where (23) is valid. Let
is the standardized mean. We now consider another example where (23) is valid. Let 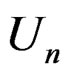 be a U-statistic of degree 2,
be a U-statistic of degree 2,

where the ’s are iid and
’s are iid and 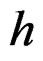 is a symmetric function of two variables with
is a symmetric function of two variables with 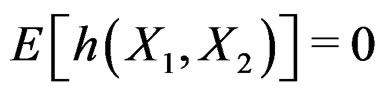 and
and 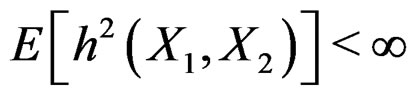 . Let
. Let 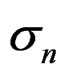 be the standard deviation of
be the standard deviation of 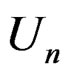 and
and 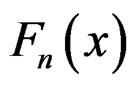 be the distribution function of
be the distribution function of , then under certain conditions [13] and [14] showed that
, then under certain conditions [13] and [14] showed that
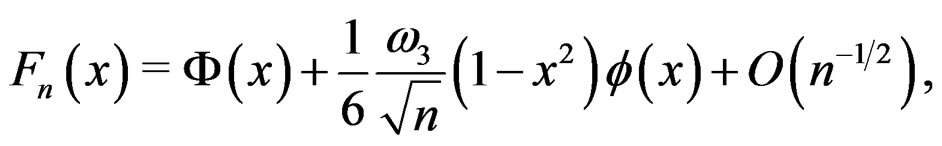 (25)
(25)
where 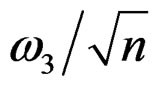 is an approximation with error
is an approximation with error  to the third cumulant of
to the third cumulant of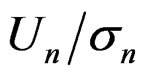 ,
, . With
. With  , (25) then implies that (23) is indeed valid. Furthermore, it can be shown that the fourth cumulant of
, (25) then implies that (23) is indeed valid. Furthermore, it can be shown that the fourth cumulant of ,
, 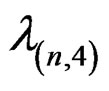 , satisfies
, satisfies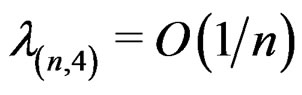 . The right-hand side of (25) and thus that of (23) can be further expanded. The expansion in (25) is simpler than that in (23) in that it is defined in terms of a simpler asymptotic sequence
. The right-hand side of (25) and thus that of (23) can be further expanded. The expansion in (25) is simpler than that in (23) in that it is defined in terms of a simpler asymptotic sequence
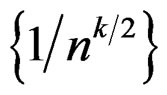 while (23) is defined in terms of
while (23) is defined in terms of 
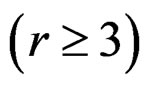 ) which may be difficult to compute. From the present point of view, however,
) which may be difficult to compute. From the present point of view, however, 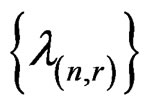 is a more natural asymptotic sequence upon which to base asymptotic expansions. Presently, it is not clear which one is more accurate for small and moderate sample sizes.
is a more natural asymptotic sequence upon which to base asymptotic expansions. Presently, it is not clear which one is more accurate for small and moderate sample sizes.
Steps similar to Steps 1 and 2 in Section 2 may be devised to derive formal expansions for the distribution function directly using the inversion formula,
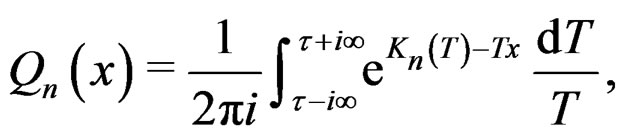 (26)
(26)
where  is the tail probability and
is the tail probability and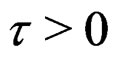 . This process, however, is more complicated due to the extra term
. This process, however, is more complicated due to the extra term 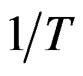 in the integrand and it leads to different expansions depending on whether or not
in the integrand and it leads to different expansions depending on whether or not  is expanded. We will not discuss such expansions here.
is expanded. We will not discuss such expansions here.
5. Concluding Remarks
For the cases of the sample mean and standardized mean, the spectrum has provided a new perspective on asymptotic expansions for density functions. It revealed that the saddlepoint expansion is the only valid expansion in the spectrum for the sample mean. It led to new expansions and provided a unified standpoint for viewing known expansions for the standardized mean. It also led to valid expansions outside the iid setting. These suggest that the spectrum is a valuable tool in finding expansions for density functions.
The derivation in Section 2 does not explicitly use the condition that 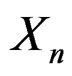 is asymptotically normal. Without this condition, however, the sequence
is asymptotically normal. Without this condition, however, the sequence  may not be an asymptotic sequence and this condition has been used implicitly in the corollaries. Our derivation also shows that to obtain a saddlepoint type of expansion it is not necessary to isolate the asymptotic factor n by expressing the cumulant generating function of
may not be an asymptotic sequence and this condition has been used implicitly in the corollaries. Our derivation also shows that to obtain a saddlepoint type of expansion it is not necessary to isolate the asymptotic factor n by expressing the cumulant generating function of 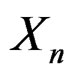 as
as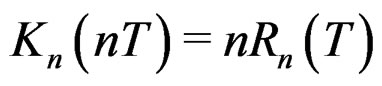 . Instead, one can use
. Instead, one can use  directly to obtain an expansion. Although the former approach will lead to the same saddlepoint approximation as the latter, it will obscure the underlying asymptotic sequence of the expansion and consequently that of the asymptotic order of the saddlepoint approximation. Indeed, the fact that the cumulant generating function can be written as
directly to obtain an expansion. Although the former approach will lead to the same saddlepoint approximation as the latter, it will obscure the underlying asymptotic sequence of the expansion and consequently that of the asymptotic order of the saddlepoint approximation. Indeed, the fact that the cumulant generating function can be written as  times a function not dependent on
times a function not dependent on 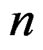 is only a coincidence in the iid case. It has made it possible to establish the validity of the saddlepoint expansion through the method of steepest descent for this case. But it is not essential for deriving a formal expansion in general.
is only a coincidence in the iid case. It has made it possible to establish the validity of the saddlepoint expansion through the method of steepest descent for this case. But it is not essential for deriving a formal expansion in general.
Turning now to some historical notes and remarks on previous work which have motivated this work. The Charlier difference series and the Gram-Charlier series of type A are mathematically elegant formal techniques which have contributed to the discovery of the Edgeworth expansion. However, they were not specifically aimed at approximating distributions from an asymptotic point of view and were unable to make use of the information that  is asymptotically normal beyond choosing the normal density function as the developing function. When the focus is on obtaining accurate approximations for the distributions of
is asymptotically normal beyond choosing the normal density function as the developing function. When the focus is on obtaining accurate approximations for the distributions of 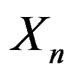 rather than obtaining the speed at which the sequence approaches normality, other developing functions may be more suitable. In the present paper, we have found the leading term of the general expansion (16) to be very useful for this purpose.
rather than obtaining the speed at which the sequence approaches normality, other developing functions may be more suitable. In the present paper, we have found the leading term of the general expansion (16) to be very useful for this purpose.
Although in the extended version of Poincaré’s definition of an asymptotic expansion,
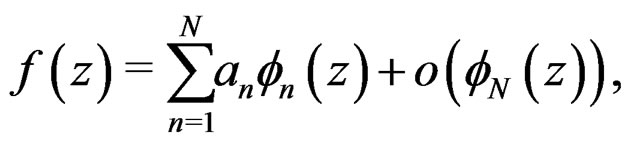
the asymptotic sequence  needs not to be a power sequence, important developments in the theory of asymptotic analysis are mostly concerned with power series expansions. The developments in asymptotic expansions in statistics reflect that of the theory of asymptotic analysis. Our use of the sequence
needs not to be a power sequence, important developments in the theory of asymptotic analysis are mostly concerned with power series expansions. The developments in asymptotic expansions in statistics reflect that of the theory of asymptotic analysis. Our use of the sequence 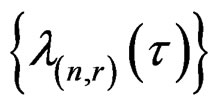 was inspired by [15,16] which have used non-power sequences to characterize the Edgeworth expansion and the saddlepoint expansion. Indeed, with an appropriate standardizetion the cumulant generating function of an asymptotically normal sequence approaches a second order polynomial. If the limiting normal distribution is not a degenerate distribution, then the sequence
was inspired by [15,16] which have used non-power sequences to characterize the Edgeworth expansion and the saddlepoint expansion. Indeed, with an appropriate standardizetion the cumulant generating function of an asymptotically normal sequence approaches a second order polynomial. If the limiting normal distribution is not a degenerate distribution, then the sequence 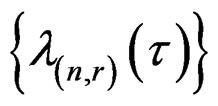 may be an asymptotic sequence which can be used to construct asymptotic expansions.
may be an asymptotic sequence which can be used to construct asymptotic expansions.
6. Acknowledgements
I would like to thank a referee for helpful comments which have led to improvements in this paper.
REFERENCES
- F. Y. Edgeworth, “The Law of Error,” Cambridge Philosophical Society Transactions, Vol. 20, 1905, pp. 33- 66.
- D. L. Wallace, “Asymptotic Approximations to Distributions,” Annals of Mathematical Statistics, Vol. 29, No. 3, 1958, pp. 635-654. doi:10.1214/aoms/1177706528
- H. Cramér, “On the Composition of Elementary Errors,” Skand Aktuarietidskr, Vol. 11, 1928, pp. 13-74.
- H. Cramér, “Random Variables and Probability Distributions,” Cambridge University Press, Cambridge, 1937.
- W. Feller, “An Introduction to Probability Theory and Its Applications,” Wiley, New York, 1966.
- R. N. Bhattacharya and J. K. Ghosh, “On the Validity of the Formal Edgeworth Expansion,” Annals of Statistics, Vol. 6, No. 2, 1978, pp. 434-451. doi:10.1214/aos/1176344134
- R. Strawderman, G. Casella and M. Wells, “Practical SmallSample Asymptotics for Regression Problems,” Journal of the American Statistical Association, Vol. 91, No. 434, 1996, pp. 643-654. doi:10.2307/2291660
- C. A. Field, “Tail Areas of Linear Combinations of ChiSquares and Non-Central Chi-Squares,” Journal of Statistical Computation and Simulation, Vol. 45, No. 3-4, 1996, pp. 243-248. doi:10.1080/00949659308811484
- H. E. Daniels, “Saddlepoint Approximations in Statistics,” Annals of Mathematical Statistics, Vol. 25, No. 4, 1954, pp. 631-649. doi:10.1214/aoms/1177728652
- M. S. Srivastava and W. K. Yau, “Tail Probability Approximations of General Statistics,” Technical Report No. 88-38, Center for Multivariate Analysis, University of Pittsburgh, Pittsburgh, 1988.
- G. S. Easton and E. Ronchetti, “General Saddlepoint Approximation with Application to
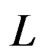 Statistics,” Journal of the American Statistical Association, Vol. 81, No. 394, 1986, pp. 420-429. doi:10.2307/2289231
Statistics,” Journal of the American Statistical Association, Vol. 81, No. 394, 1986, pp. 420-429. doi:10.2307/2289231 - R. D. Routledge and M. Tsao, “Uniform Validity of Saddlepoint Expansion on Compact Set,” Canadian Journal of Statistics, Vol. 23, No. 4, 1995, pp. 425-431. doi:10.2307/3315386
- H. Callaert, P. Janssen and N. Veraverbeke, “An Edgeworth Expansion for U-Statistics,” Annals of Statistics, Vol. 8, No. 2, 1980, pp. 299-312. doi:10.1214/aos/1176344955
- P. J. Bickel, F. Götze and W. R. van Zwet, “The Edgeworth Expansion for U-Statistic of Degree Two,” Annals of Statistics, Vol. 14, No. 4, 1986, pp. 1463-1484. doi:10.1214/aos/1176350170
- I. M. Skovgaard, “On Multivariate Edgeworth Expansions,” International Statistical Review, Vol. 54, No. 2, 1986, pp. 169-186. doi:10.2307/1403142
- J. L. Jensen, “Saddlepoint Approximations,” Clarendon Press, Oxford, 1995.
- M. G. Kendall and A. Stuart, “Advanced Theory of Statistics,” 3rd Edition, High Wycombe, London, 1969.
Appendix. Proof of Lemma 1
We need the following identities which may be found in [17]:
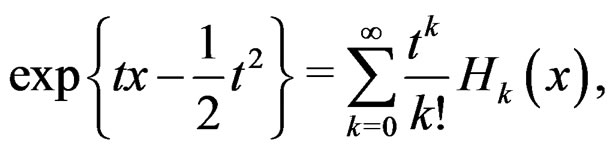 (27)
(27)
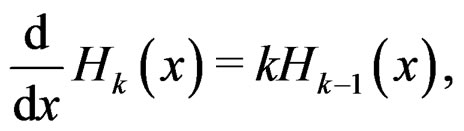 (28)
(28)
where 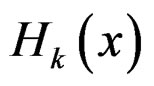 is the Hermite polynomial of degree
is the Hermite polynomial of degree  and by convention
and by convention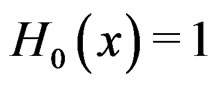 .
.
By setting 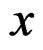 to zero in (27) we obtain
to zero in (27) we obtain
 (29)
(29)
The left-hand side of (29) is the moment generating function of the standard normal distribution evaluated at . It follows that
. It follows that
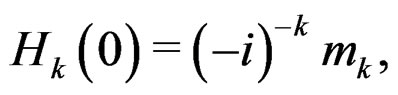 (30)
(30)
for , where
, where 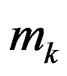 is the
is the 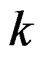 th moment of the standard normal distribution. Since
th moment of the standard normal distribution. Since 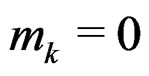 when
when  is odd, (30) may be written as
is odd, (30) may be written as
 (31)
(31)
To prove (2), we show that if  satisfies
satisfies
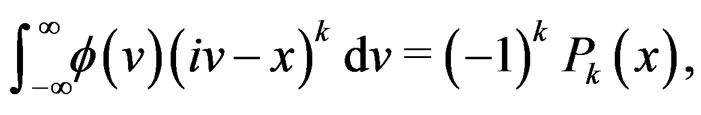 (32)
(32)
for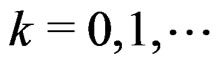 , then
, then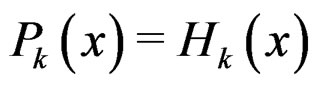 . We first note that
. We first note that
 (33)
(33)
Again, since 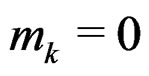 when
when 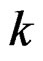 is odd, (33) may be written as
is odd, (33) may be written as
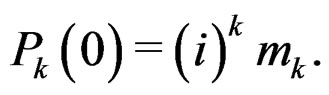 (34)
(34)
Furthermore, by differentiating (32) with respect to  we obtain
we obtain

for . Thus
. Thus
 (35)
(35)
for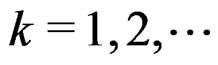 . It follows that
. It follows that 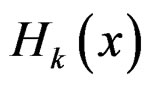 and
and  are the solutions of the same differential Equation (28) or (35). Furthermore,
are the solutions of the same differential Equation (28) or (35). Furthermore, 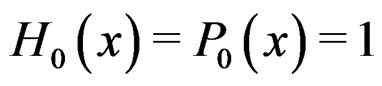 and
and 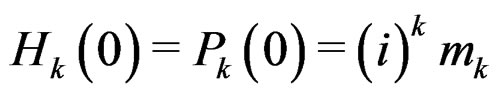 , by induction
, by induction 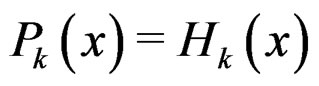 for
for .
.

