ABSTRACT

Let 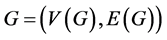be an undirected graph. The maximum cycle packing problem in G then is to find a collection 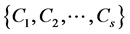of edge-disjoint cycles 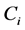in G such that s is maximum. In general, the maximum cycle packing problem is NP-hard. In this paper, it is shown for even graphs that if such a collection satisfies the condition that it minimizes the quantity on the set of all edge-disjoint cycle collections, then it is a maximum cycle packing. The paper shows that the determination of such a packing can be solved by a dynamic programming approach. For its solution, an 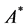-shortest path procedure on an appropriate acyclic network 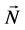is presented. It uses a particular monotonous node potential.

Keywords:

Maximum Edge-Disjoint Cycle Packing, Extremal Problems in Graph Theory, Dynamic Programming, -Shortest Path Procedure

1. Introduction

We consider a finite and undirected graph G with vertex set 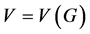and edge-set 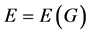that contain no loops.

For a finite sequence 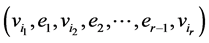of vertices and pairwise distinct edges 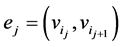the subgraph W of G with vertices and edges 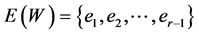is called a walk with start vertex 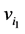and end vertex.

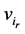If W is closed, i.e.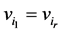, we call it a circuit in G. A path is a walk in which all vertices v have degree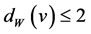. A cycle is a closed path. The length of a cycle is denoted by. An even graph is a graph G in which all vertices v have even degree. An Eulerian graph is a connected even graph.

For, let be subgraphs of G. We say G is induced by if and . Two subgraphs, are called edge-disjoint if. For, we define. For, we define, where and.

A packing of G is a collection of subgraphs of G () such that all are mutually edge-disjoint and G is induced by. If exactly s of the is cycles, is called a cycle packing of cardinality. The family of cycle-packings of cardinality s is denoted by. If the cardinality of a cycle packing is maximum, it is called a maximum cycle packing. Its card- inality is denoted by. If no confusion is possible, we will write instead of and instead of, respectively.

Packing edge-disjoint cycles in graphs is a classical graph-theoretical problem. There is a large amount of literature concerning conditions that are sufficient for the existence of certain numbers of disjoint cycles which may satisfy some further restrictions. An overview of related references is given in [1] . Practical applications of cycle packings are mentioned in the papers [2] [3] [4] [5] . The algorithmic problems concerning the construction of maximum edge-disjoint cycle packings are typically hard (e.g. see [6] [7] [8] ). A simple greedy-type heuristic for the problem is presented in [7] , which iteratively looks for cycles of small length and removes the corresponding edges from the current graph until there is no cycle left. A different approach to tackle the problem is to relate maximum cycle packings of G to maximum cycle packings of subgraphs of G. In [1] it is described how can be obtained if G has a vertex cut-set S of cardinality k. In this case, can be determined by the values for at most

graphs of order smaller than G. Let denote the cyclomatic number of G, i.e., where c denotes the number of connected components of G. If is known, then [9] shows how to construct G from one of a finite number of graphs by a series of simple graph operations. The paper [10] investigates a relation between a maximum cycle packing and maximum local traces for the case that G is Eulerian. For, an Eulerian subgraph of G is called a local trace (at v) if every walk with start vertex v can be extended to an Eulerian tour in. Traces were first considered in [11] and [12] .

In [13] bounds on are presented if G is a polyhedral graph. These bounds depend on the size, the order or the number of faces of G, respectively. Polyhedral graphs are constructed that attain these bounds.

In the present paper, we will consider even graphs and tackle the cycle packing problem by a dynamic programming approach. The main idea is, instead of regarding the length of a cycle, to consider its square. Doing so, a cycle packing of cardinality s with cycles can be scored by

In Section 2, we prove a max-min theorem that relates a minimizer of L to a maximum cycle packing of G. This theorem gives reason to consider maximum cycle packing problems of G within the framework of dynamic programming. In section 3, therefore, the problem is transformed into a shortest path problem on some ap- propriate acyclic networks. In order to avoid unnecessary excessive calculations in, suitable bounds on the length of an optimal paths are used. These bounds can be incorporated into an -algorithm. The algorithmic scheme of the procedure is presented in Section 3.2.

2. A Max-Min Theorem

Let. A cycle packing then can be represented by

(if) where the are the s cycles and is the uniquely determined remainder graph induced by. If no confusion is possible, we will write instead of. For,. For, might still contain cycles of G. For an even graph G, it may occur that also in cases that. In these cases, we will write. If G is non-even, for all.

For, define

For, set.

For the purpose of proving the crucial Lemma 1, consider particular subsets of, defined by

1)

2) For, a packing if and only if its reminder graph contains a cycle.

We then get

Lemma 1. Let G be even, , and let be the graph induced by G and a single edge as an additional component. For, define

Then

Proof. It can easily be seen that and.

We will use induction on.

. Let such that. Since is the graph induced by and, must contain a cycle of length. Obviously,. Then

.

Now, let and let us assume that for all even graphs G such that the strict inequalities hold.

Let G be an even graph such that. We will show for all.

Let such that. Consider the graphs and. is even and. Obviously, and. But also must hold, otherwise would not be a minimizer of L on.

Hence,. Applying the induction assumption to, we then get:

Here is a minimizer of L on. From this we finally conclude

By, we denote the family of all cycle packings of G. We get

Theorem 1. Let G be even,. Every cycle packing that minimizes L on is maximum, i.e..

Proof. Let be a minimizer of L on. We can assume that We will show that.

For this, consider the non-even graph obtained by adding a component and an additional edge to G. Obviously, is even and. For the packing with it holds and. We will show .

For an arbitrary packing, the remainder is the dis- joint union of and some even graph H that contains at least one cycle of length. Let.

If the component is not contained in H, then is one of the cycles, i.e.. In this case C is a cycle in G.

Consider the packing Then . We get

i.e.

We conclude, that there must be a minimizer of L on, such that. Obviously, , i.e. with.

We get

Applying Lemma 1 to the even graph, we get for:

where the last inequality is strict if.

Now, let be a maximum cycle packing that mini-

mizes L on, i.e..

Then with minimizes L on

. Obviously,. We get

where the inequality is strict, if.

It follows. But was a minimizer on, i.e.. Therefore, and.

A maximum cycle packing of G is said to be max-min if it minimizes L on. The quantity is the max-min cycle value of G. The determination of a max-min cycle packing will be called the max-min cycles packing problem (mmcp-problem) of G. Clearly, max-min cycle packings, in general, are not unique.

The following theorem relates the determination of to the determination of the max-min cycle values for even subgraphs.

Theorem 2. Let G be even. Then

Proof. Let be an even subgraph of G and be max-min.

A packing then induces a

packing. We then get

and conclude

Now, let be max-min and let and be induced by and, respectively.

The packings and must also be max-min. We get

The proof of Theorem 2 immediately induces

Corollary 1.

1), for every even subgraph H of G.

2).

3. A Shortest Path Approach for the MMCP-Problem

Theorem 2 gives reason to treat the mmcp-problem as a shortest path problem within a suitable weighted acyclic network

3.1. The MMCP-Network

Let the edges in E be labelled, i.e.. In a canonical way, a subgraph is determined by its incidence vector

i.e.,

Let and.

¹For we will use “nodes”, in G we use “vertices”.

We will identify the set X of nodes¹ in with the set of even subgraphs of G. Each node corresponds to some specific even subgraph H of G (we will write). Nodes in are also assigned to stages, i.e. .

For the construction of, the nodes and edges are defined inductively:

・ The unique node in corresponds to the subgraph of G with empty edge set. Assume that the set of nodes is given. Then a node belongs to if there is such that

We call to be a successor of. The set of all successors of is called an expansion of, and a specific successor is generated by expanding.

・ An edge in U corresponds to some specific cycle in G. Edges exist only between nodes at consecutive stages. An edge if and only if for the cor- responding subgraphs is a successor of.

・ As edge weights we set.

Clearly, is acyclic and the number of stages in cannot exceed. An even subgraph is reachable in if there is a path with starting node and end node H. In a canonical way, any path induces a cycle packing. The set describes the cycles used in the successive expansions of the corresponding nodes.

Obviously, G is reachable in, but not all even subgraphs of G have this property. Hence, not every cycle packing is induced by some paths. We get

Lemma 2. Let be reachable in and be a cycle-packing of H of cardinality s. Then there is a path in that induces.

Proof. Let be a cycle packing of H of cardinality. Without loss of generality, we can assume that the cycles in are ordered such that. Let and be the even subgraph of H induced by. Since the cycles are mutually edge-disjoint, the number coincides with. Therefore, is generated by an expansion of, i.e. there is a path that induces. Moreover, if and are two different cycle-packings of H, then the corresponding paths in must be different.

Together with Theorem 1, we conclude for the special case:

Proposition 3. is a max-min cycle packing of G if and only if corresponds to a shortest path in.

In order to reduce the number of graphs that have to be expanded within the algorithmic procedure, those subgraphs H in have to be identified that cannot be contained in. Such an identification, preferably, should be done as early as possible in the calculations. The following proposition gives conditions for such a situation. They can be checked during the shortest path procedure. If such a condition is satisfied, H must never be expanded.

Proposition 4. Let be a shortest path in and let be reachable. If

1) or

2)

holds, then

Proof. Since, holds. Assume that. Then there is a cycle packing induced by. The packing, therefore, must be max-min. Hence,. This leads to the contradiction.

3.2. An A^*-Shortest Path Algorithm

For an even subgraph, let denote the length of the shortest cycle in H, then,

is a lower bound for the max-min cycle value. Moreover, the function is a monotonous node potential on in the following sense

Lemma 3. For, let be two even subgraphs of G adjacent in such that. Then

Proof. Let and be the lengths of the shortest cycles in and, respectively. Then

The last inequality is true, since. Hence,

In [14] , it is described how information of a monotonous node potential could be incorporated into a searching strategy for the shortest path procedure. Such an - search algorithm constructs successively and expands only such nodes that are candidates for a shortest path.

The procedure essentially manages two sets of nodes in and updates several quantities:

・ X: even subgraphs of G that are candidates to determine.²

・ L: subgraphs that are already expanded. For, a shortest path is already constructed.

・ : index of the stage in at which H is considered. If terminates, is the cardinality of a maximum cycle packing.

・ : (currently) the shortest length of a path. If, then. If stops,.

・ : monotonous node potential.

The scheme of such an -search is outlined as follows.

The determination of in step 1 requires the determination of the girth of. This can efficiently be done by the shortest paths procedures. For the expansion of H in step 2, the value and the set C of all cycles in that contain must be generated. This makes it necessary to identify all simple paths between u and v in the graph. Typically, this subproblem is attacked by using DFS procedures. In general, it is NP-hard ( [15] ).

Step 3 incorporates the stopping rule () and the elimination of super- fluous nodes (and sub-paths) according to Prop. 4.

Coming from step 2, terminates in step 3 if G is expanded from some H for the first time. Since it is possible that the graph G may appear in at different stages, it must be guaranteed that doesn’t stop at a “wrong” node that corresponds to G.

Proposition 5. If stops, then is a max-min cycle packing of G.

Proof. Assume, terminates and. In this case cor- responds to a node at stage. Since the corresponding cycle packing is not maximum,. Let be the path in induced by and let be the predecessor of on that path.

The only node in at stage corresponds to G (). For the shortest path, Theorem 1 gives.

Let be the last common node of the paths and. Since is expanded at some iteration of, there must be a subgraph on the subpath of that belongs to X when terminates. Since this node is never selected in step 1 until stops (otherwise it would have been deleted from X in step 2), the inequality must hold. But then

is a contradiction. Hence, terminates at stage, i.e. is maximum.

Acknowledgements

We thank the Editor and the referees for their comments.

Cite this paper

Recht, P. (2016) A Dynamic Programming Approach for the Max-Min Cycle Packing Problem in Even Graphs. Open Journal of Discrete Mathematics, 6, 340-350. http://dx.doi.org/10.4236/ojdm.2016.64027

References

NOTES

²We will write “H Î X”, indicating that the node that corresponds to H belongs to X.