Open Journal of Discrete Mathematics
Vol.3 No.3(2013), Article ID:34517,5 pages DOI:10.4236/ojdm.2013.33029
Multiple Circular Colouring as a Model for Scheduling
Department of Mathematics, Trent University, Peterborough, Canada
Email: bzhou@trentu.ca
Copyright © 2013 Bing Zhou. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 30, 2013; revised May 31, 2013; accepted June 15, 2013
Keywords: Graph Coloring; Circular Chromatic Number; Fractional Chromatic Number; Multi-Circular Coloring; Scheduling Problem
ABSTRACT
In this article we propose a new model for scheduling periodic tasks. The model is based on a variation of the circular chromatic number, called the multiple circular colouring of the conflict graph. We show that for a large class of graphs, this new model will provide better solutions than the original circular chromatic number. At the same time, it allows us to avoid the difficulty of implementation when the fractional chromatic number is used.
1. Introduction
We consider the scheduling problems involving tasks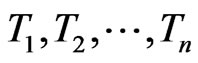 . If two tasks both use a common resource, they cannot be scheduled at the same time. A valid scheduling is a mapping f from
. If two tasks both use a common resource, they cannot be scheduled at the same time. A valid scheduling is a mapping f from 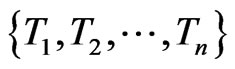 to the subsets of a time period [0,T] such that
to the subsets of a time period [0,T] such that
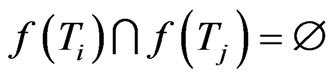 if
if 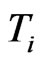 and
and 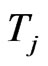 use a common resource. Let the value of a scheduling f be
use a common resource. Let the value of a scheduling f be
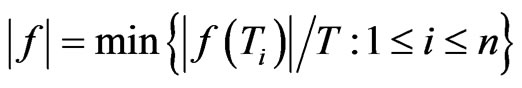 , which is the minimum length of time a task has been assigned normalized by the length of the time period. The goal is to find a scheduling
, which is the minimum length of time a task has been assigned normalized by the length of the time period. The goal is to find a scheduling 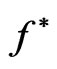 that maximizes
that maximizes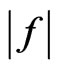 . One example of this type of scheduling problem is the heavily loaded resource sharing system in computer science [1-3]. The tasks are processes and some of them may share a common data file. Two processes that do share a common data file cannot operate at the same time. A scheduling of the processes that has the maximum value would allow the processes to operate most efficiently.
. One example of this type of scheduling problem is the heavily loaded resource sharing system in computer science [1-3]. The tasks are processes and some of them may share a common data file. Two processes that do share a common data file cannot operate at the same time. A scheduling of the processes that has the maximum value would allow the processes to operate most efficiently.
The constraints of the scheduling problem can be represented by a graph, called the conflict graph. The conflict graph G has vertex set 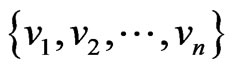 representing the tasks where two vertices vi and vj are adjacent if and only if they use at least one common resource. Vertex colouring and chromatic numbers of the conflict graph have been used as models for scheduling problems (see for example [4]). If G can be coloured with kcolours such that no two adjacent vertices have the same colour, we can then divide [0,T] into k equal length periods. All vertices that are coloured with the same colour do not have edges between them and therefore can be assigned to one period. For this scheduling f, we have
representing the tasks where two vertices vi and vj are adjacent if and only if they use at least one common resource. Vertex colouring and chromatic numbers of the conflict graph have been used as models for scheduling problems (see for example [4]). If G can be coloured with kcolours such that no two adjacent vertices have the same colour, we can then divide [0,T] into k equal length periods. All vertices that are coloured with the same colour do not have edges between them and therefore can be assigned to one period. For this scheduling f, we have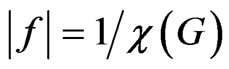 . Thus in general
. Thus in general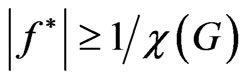 .
.
When the tasks are periodic in nature, circular colouring of the conflict graph is a more appropriate method. Circular colouring and the circular chromatic number (also called the star chromatic number) were introduced by A. Vince in 1988 [5]. A (k,d)-circular-colouring of a graph G is a mapping 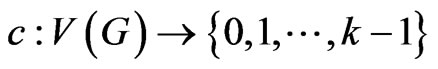 such that for each edge xy in G,
such that for each edge xy in G,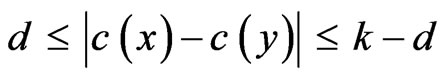 .
.
The circular chromatic number of G, 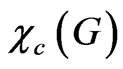 , is the infimum of the ratio k/d for which G has a (k,d)-circularcolouring.
, is the infimum of the ratio k/d for which G has a (k,d)-circularcolouring.
Equivalently, we can consider a (k,d)-circular-colouring of G as a mapping c from V(G) to the open arcs of length d in a circle of length k such that if xy is an edge in G,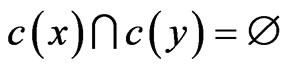 . If we assign the tasks using a (k,d)- circular-colouring of the conflict graph G, we would have
. If we assign the tasks using a (k,d)- circular-colouring of the conflict graph G, we would have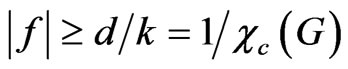 .
.
A (k,d)-set-colouring of a graph G is a mapping c such that for every vertex v in G, c(v) is a d-subset of
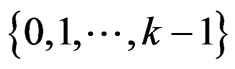 and if xy is an edge in G,
and if xy is an edge in G,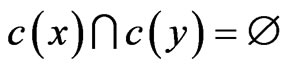 . The fractional chromatic number of a graph G,
. The fractional chromatic number of a graph G, 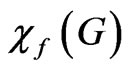 , is the infimum of the ratio (k/d) for which G has a (k,d)-set-colouring. If we can consider a (k,d)-set-colouring as a mapping c from V(G) to the sets of arcs in the circle of length k such that the length of the union of arcs in f(v) is at least d for every vertex v and if xy is an edge inG,
, is the infimum of the ratio (k/d) for which G has a (k,d)-set-colouring. If we can consider a (k,d)-set-colouring as a mapping c from V(G) to the sets of arcs in the circle of length k such that the length of the union of arcs in f(v) is at least d for every vertex v and if xy is an edge inG,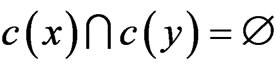 . An assignment using a (k,d)-set-colouring of the conflict graph G would yield
. An assignment using a (k,d)-set-colouring of the conflict graph G would yield
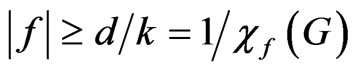 .
.
Circular chromatic number and fractional chromatic number and their variations have been extensively studied in the last two decades [6-11]. More results on the circular chromatic number and fractional chromatic number can be found in the book [12] and the survey papers [13,14]. It is easy to see that by their definition, we have the relations
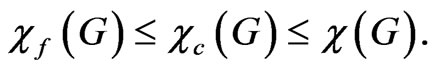
Vince proved in [5] that

Therefore, we have
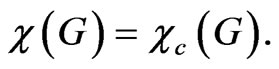
While the difference between 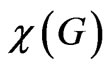 and
and 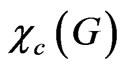 is always less than 1, it is known that the difference between
is always less than 1, it is known that the difference between 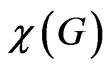 and
and 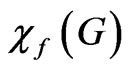 can be arbitrarily large for some graphs. An example is the family of graphs called Kneser graphs. A Kneser graph ([15,16])
can be arbitrarily large for some graphs. An example is the family of graphs called Kneser graphs. A Kneser graph ([15,16]) 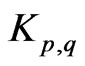 has all q-subsets of
has all q-subsets of 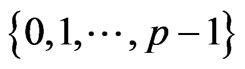 (p > 2q) as its vertices and two vertices are adjacent if the two subsets are disjoint. It is proved in [16] that
(p > 2q) as its vertices and two vertices are adjacent if the two subsets are disjoint. It is proved in [16] that
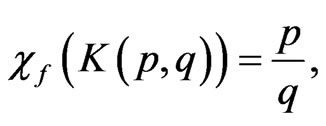
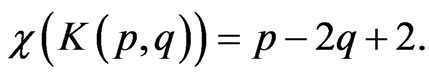
Another example of a family of graphs where the difference between their chromatic number and fractional chromatic number is large is the graphs obtained by using Mycielski’s construction.
For a graph G with vertex set 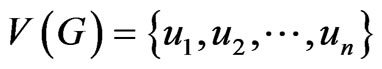 and edge set
and edge set , the Mycielskian
, the Mycielskian 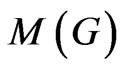 of G is the graph with vertex set
of G is the graph with vertex set
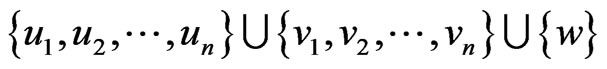 and edge set
and edge set
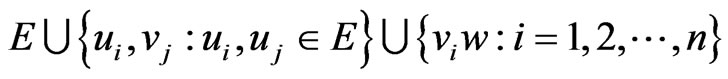 .
.  in
in
Figure 1 is also called the Grotzsch graph.
It is well known that
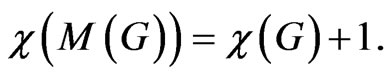
For the fractional chromatic number of Mycielskians, the authors of [17] found the recurrence relation

For the Grotzsch graph, since 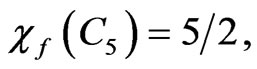 we have
we have
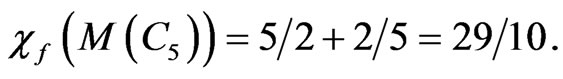
We use the notation 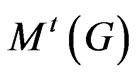 such that
such that
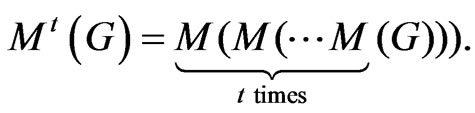
We have

Figure 1. Grotzsch graph.
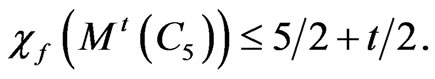
In comparison, we have
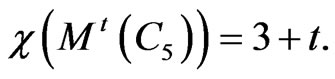
For this class of graphs, the difference between 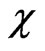 and
and 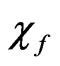 is unbounded.
is unbounded.
For the circular chromatic number, we have
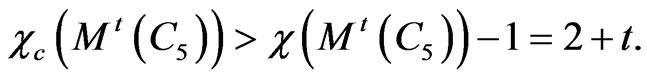
This shows that the difference between the circular chromatic number and the fractional chromatic number is also arbitrarily large for the Mycielskians. To achieve the optimal result for a scheduling problem in general, it appears that the fractional chromatic number of the conflict graph provides the best results.
However, there are difficulties if we use (k,d)-set colouring and the fractional chromatic number in the scheduling problem. To achieve 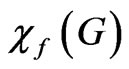 the optimal (k,d)-set colouring may have a very large value of d. As pointed out in [12],
the optimal (k,d)-set colouring may have a very large value of d. As pointed out in [12], 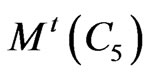 is an example of a graph G for which
is an example of a graph G for which 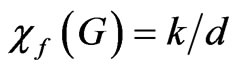 for no small d. In fact, if we let
for no small d. In fact, if we let 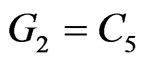 and
and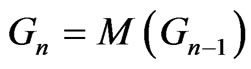 , then
, then
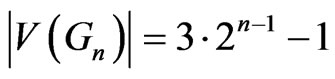
and 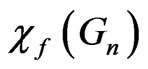 is a fraction whose denominator, when written in smallest terms, is greater than
is a fraction whose denominator, when written in smallest terms, is greater than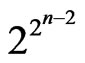 . This example shows that there is no bound on the denominator of
. This example shows that there is no bound on the denominator of 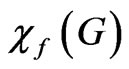 that is a polynomial function of the number of vertices of G. If this optimal set colouring is to be used for scheduling, each task would be divided into too many fragments making it impossible in practice. To combine optimality and practicality, in the next section we propose a new colouring of the conflict graph that will provide a better solution than the circular colouring and easier to implement than the set colouring.
that is a polynomial function of the number of vertices of G. If this optimal set colouring is to be used for scheduling, each task would be divided into too many fragments making it impossible in practice. To combine optimality and practicality, in the next section we propose a new colouring of the conflict graph that will provide a better solution than the circular colouring and easier to implement than the set colouring.
2. Multiple Circular Colouring of a Graph
Definition 1 An m-(k,d)-circular colouring of a graph G is a mapping c from V(G) to the sets of open arcs in the circle of length k such that c(v) is the union of m arcs with a total length at least d and if xy is an edge in G, 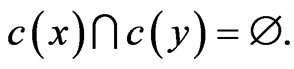 The m-circular chromatic number,
The m-circular chromatic number, 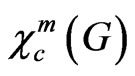 is the infimum of the ration
is the infimum of the ration 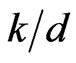 for which Ghas a m-(k,d)-circular-colouring.
for which Ghas a m-(k,d)-circular-colouring.
It is easy to see that for every positive integer m,
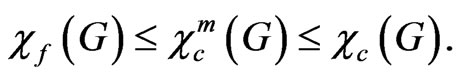
To demonstrate this colouring indeed improves the solution of the scheduling problem in some cases, we show that even for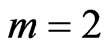 ,
, 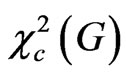 can be strictly less than
can be strictly less than 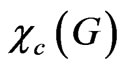 for large classes of graphs.
for large classes of graphs.
Recall that for a graph G, M(G) is the Mycielskian of G. There are many graphs G such that 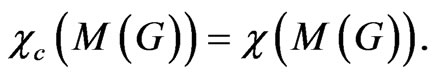 Some sufficient conditions for this equality to hold are given in, for example, [18] and [19]. However,
Some sufficient conditions for this equality to hold are given in, for example, [18] and [19]. However, 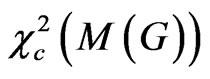 will always be strictly less than
will always be strictly less than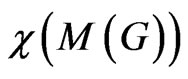 .
.
Theorem 2 For every graph G,
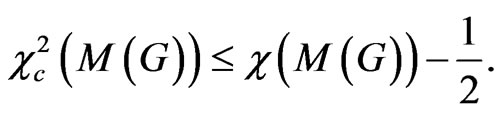
Proof: Let 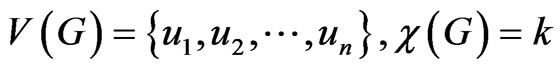 and
and
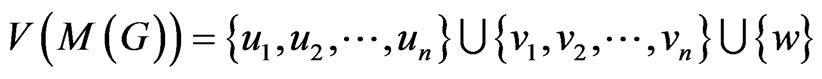 as described in the previous section. Let
as described in the previous section. Let  be a circle of length k. Since
be a circle of length k. Since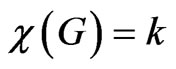 , there is a mapping of the form
, there is a mapping of the form 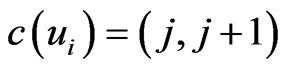 for each i where
for each i where
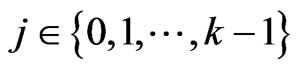 such that
such that 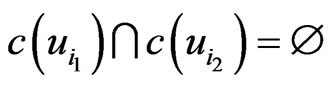 whenever
whenever 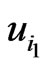 and
and 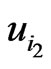 are adjacent.
are adjacent.
Let 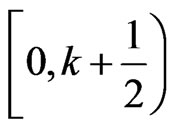 be a circle of length
be a circle of length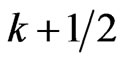 . Let
. Let
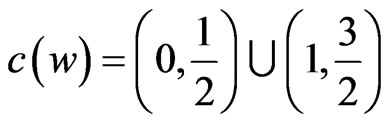 . Notice that
. Notice that 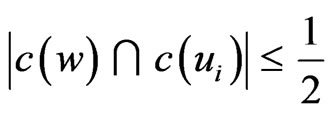
for all i. Figure 2 demonstrates this mapping when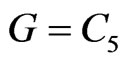 .
.
For each i, if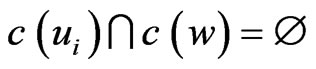 , let
, let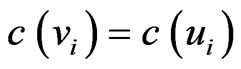 ;
;
otherwise, let 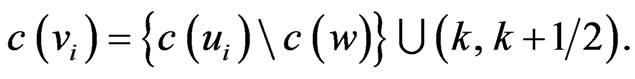 We show that the arcs representing these vertices in the case of
We show that the arcs representing these vertices in the case of 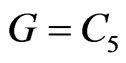 in Figure 3.
in Figure 3.
It is easy to check that this is a valid 2-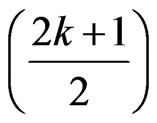 -circular colouring of M(G) in general. This proves that
-circular colouring of M(G) in general. This proves that
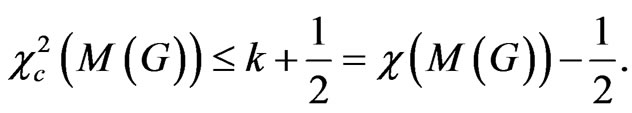
Corollary 3 If 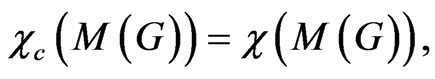 then
then
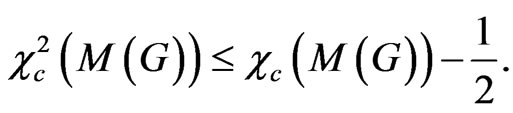
Next we show that unlike the set-chromatic number, the denominator of the m-circular chromatic number is bounded by the product of m and the number of vertices in the graph.
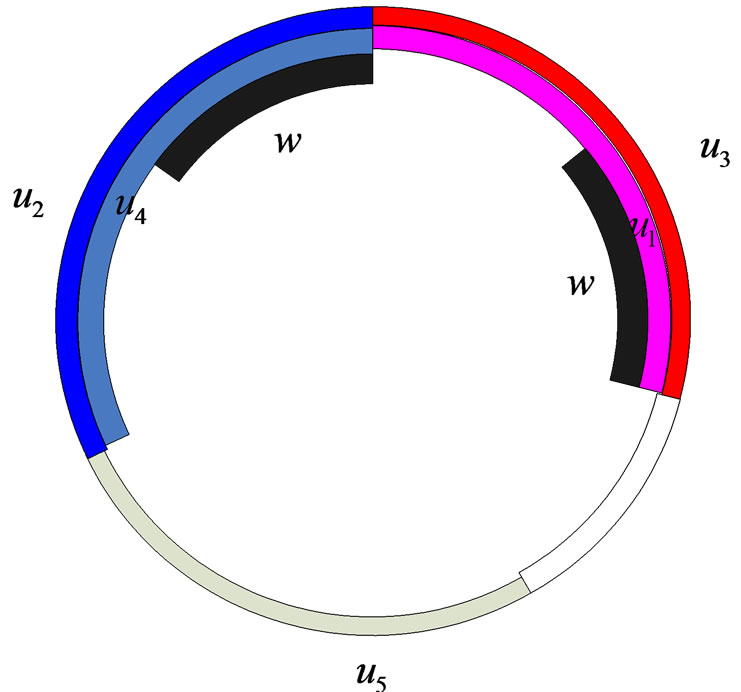
Figure 2. A 2-circhular coloring of vertices of C5 and w in M (C5).
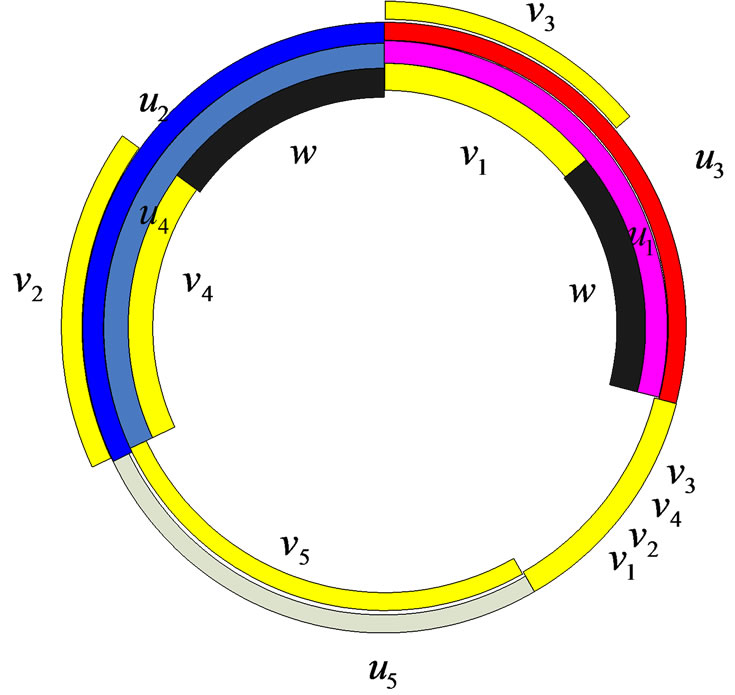
Figure 3. A 2-circular coloring of M (C5).
Theorem 4 Let G be a graph of n vertices, and
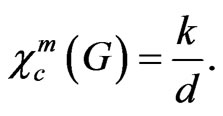 Then k and d can be integers such that d <
Then k and d can be integers such that d <
mn.
Proof: Suppose that 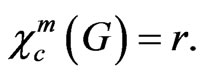 By scaling if necessary, there is a m-circular colouring c that maps the vertices of G to sets of m arcs in a circle of length r such that each arc has length at least
By scaling if necessary, there is a m-circular colouring c that maps the vertices of G to sets of m arcs in a circle of length r such that each arc has length at least 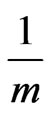 and if xy is an edge then
and if xy is an edge then
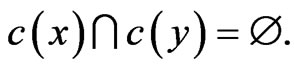 We assume that c is a colouring such that the set
We assume that c is a colouring such that the set

is the smallest. We fix a direction of the circle, say counter clockwise.
There is at least one arc l such that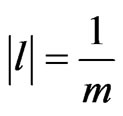 ; otherwise r could be made smaller. Let that arc be l1. There must be an arc
; otherwise r could be made smaller. Let that arc be l1. There must be an arc 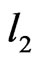 such that i)
such that i) 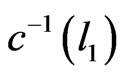 is adjacent to
is adjacent to 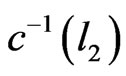 in G, ii) the left end of l1 is the right end of
in G, ii) the left end of l1 is the right end of 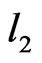 and iii)
and iii)
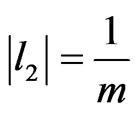 , otherwise
, otherwise 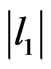 could be made larger.
could be made larger.
Continuing this process, some arc will have to be used more than once. Say the first time this happens is at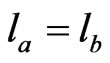 . Then the arcs
. Then the arcs 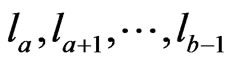 must cover the circle an integer number of times. Suppose that they cover the circle s times. Since there are
must cover the circle an integer number of times. Suppose that they cover the circle s times. Since there are 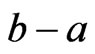 arcs and they all have length
arcs and they all have length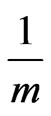 , we have
, we have
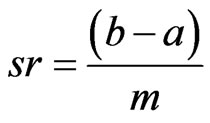
and
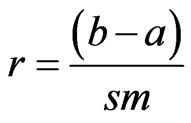
Since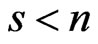 , the denominator is less than mn.
, the denominator is less than mn.
Intuitively, when the value of m increases, the m-circular chromatic number will be closer to the fractional chromatic number and thus the difference between the chromatic number and m-circular chromatic number would increase. Nevertheless, our next theorem shows that the m-circular chromatic number cannot be less than one m-th of the .chromatic number.
Theorem 5 For every graph G, 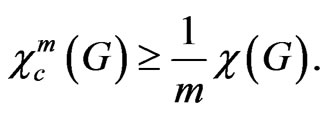
Proof: Suppose that 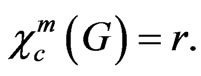 There is an m-circular colouringc such that
There is an m-circular colouringc such that 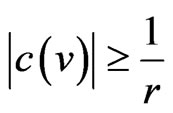 for every vertex v.
for every vertex v.
Since c(v) is a union of m arcs, at least one of the arcs has length at least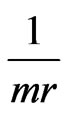 . We insert mr points
. We insert mr points 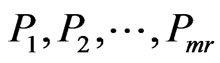
spaced at equal distance in the unit length circle. For every vertex v, c(v) contains at least one of these points. Let 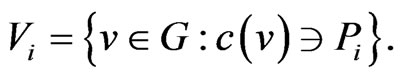 Each
Each 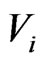 is an independent set and
is an independent set and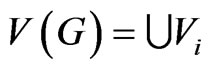 . G can be coloured with mrcolours. So we have
. G can be coloured with mrcolours. So we have
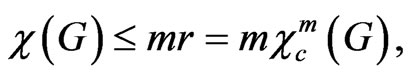
i.e., 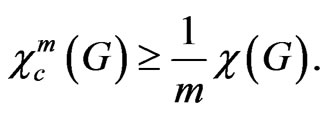
The Kneser graphs provide examples showing this lower bound is asymptotically the best possible.
Let 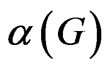 be the independence number of G.
be the independence number of G. 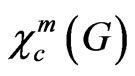 is also bounded by a function of
is also bounded by a function of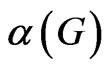 . The proof above yields a lower bound for
. The proof above yields a lower bound for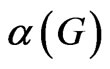 .
.
Theorem 6 For every graph G with n vertices,
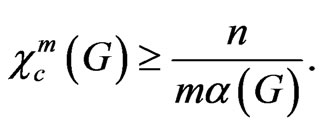
Proof: The set 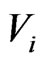 in the proof of Theorem 5 is an independent set. We have
in the proof of Theorem 5 is an independent set. We have 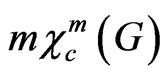 such independent sets. The average size of one set is
such independent sets. The average size of one set is 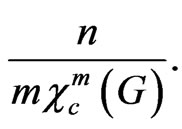 Therefore
Therefore
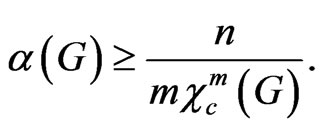
and
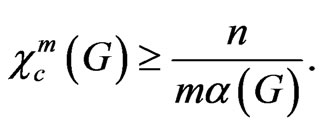
3. Conclusion
We proved that for a large class of graphs, this multiple circular colouring and m-circular chromatic number of the conflict graph will provide better solutions for the scheduling problem than the original circular chromatic number. It is also easier to implement than the model using the fractional chromatic number. We plan to investigate more classes of graph G where 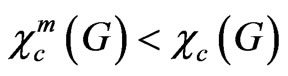 for small values of m. It would also be interesting to find out the probability for random graphs to have m-circular chromatic number strictly less than their circular chromatic number.
for small values of m. It would also be interesting to find out the probability for random graphs to have m-circular chromatic number strictly less than their circular chromatic number.
REFERENCES
- V. C. Barbosa and E. Gafni, “Concurrency in Heavily Loaded Neighborhood-Constrained Systems,” ACM Transactions on Programming Languages and Systems, Vol. 11, No. 4, 1989, pp. 562-584. doi:10.1145/69558.69560
- H. G. Yeh, “A Connection between Circular Colorin and Periodic Schedules,” Discrete Applied Mathematics, Vol. 157, No. 7, 2009, pp. 1663-1668. doi:10.1016/j.dam.2008.10.003
- H. G. Yeh and X. Zhu, “Resource-Sharing System Scheduling and Circular Chromatic Number,” Theoretical Computer Science, Vol. 332, No. 1-3, 2005, pp. 447-460. doi:10.1016/j.tcs.2004.12.005
- F. Chung, “Graph Theory in the Information Age,” Notices of AMS, Vol. 57, No. 6, 2010, pp. 726-732.
- A. Vince, “Star Chromatic Number,” Journal of Graph Theory, Vol. 12, No. 4, 1988, pp. 551-559. doi:10.1002/jgt.3190120411
- H. L. Abbott and B. Zhou, “The Star Chromatic Number of a Graph,” Journal of Graph Theory, Vol. 17, No. 3, 1993, pp. 349-360. doi:10.1002/jgt.3190170309
- H. Hatami and R. Tusserkani, “On the Complexity of the Circular Chromatic Number,” Journal of Graph Theory, Vol. 47, No. 3, 2004, pp. 226-230. doi:10.1002/jgt.20022
- K. Kilakos and B. Reed, “Fractionally Colouring Total Graphs,” Combinatorica, Vol. 13, No. 4, 1993, pp. 435- 440. doi:10.1007/BF01303515
- D. Kral, E. Macajova and J.-S. Sereni, “Circular EdgeColoring of Cubic Graphs with Girth Six,” Journal of Combinatorial Theory, Series B, Vol. 100, No. 4, 2010, pp. 351-358. doi:10.1016/j.jctb.2009.10.003
- I. Leader, “The Fractional Chromatic Number of Infinite Graphs,” Journal of Graph Theory, Vol. 20, No. 4, 1995, pp. 411-418. doi:10.1002/jgt.3190200404
- B. Zhou, “Some Theorems Concerning the Star Chromatic Number of a Graph,” Journal of Combinatorial Theory, Series B, Vol. 70, No. 2, 1997, pp. 245-258. doi:10.1006/jctb.1996.1738
- E. R. Scheinerman and D. H. Ullman, “Frational Graph Theory,” John Wiley and Sons, New York, 1997.
- X. Zhu, “Circular Chromatic Number—A Survey,” Discrete Mathematics, Vol. 229, No. 1-3, 2001, pp. 371-410. doi:10.1016/S0012-365X(00)00217-X
- X. Zhu, “Recent Developments in Circular Colouring of Graphs,” Algorithms and Combinatorics, Vol. 26, Springer, Berlin, Heidelberg, 2006, pp. 497-550.
- M. Knser, “Aufgabe 300,” Jahresbericht der Deutsche Mathematiker-Vereinigung, Vol. 58, No. 2, 1955, p. 27.
- L. Lovasz, “Kneser’s Conjecture, Chromatic Number, and Homotopy,” Journal of Combinatorial Theory, Series A, Vol. 25, No. 3, 1978, pp. 319-324. doi:10.1016/0097-3165(78)90022-5
- M. Lasen, J. Propp and D. H. Ullman, “The Fractional Chromatic Number of Mycielski Graphs,” Journal of Graph Theory, Vol. 19, No. 3, 1995, pp. 411-416. doi:10.1002/jgt.3190190313
- G. Chang, “Circular Chromatic Numbers of Mycielski’s Graphs,” Discrete Mathematics, Vol. 205, No. 1-3, 205, 1999, pp. 23-37. doi:10.1016/S0012-365X(99)00033-3
- H. Jajiaholhassan and X. Zhu, “Circular Chromatic Number and Mycielski Construction,” Journal of Graph Theory, Vol. 44, No. 2, 2003, pp. 106-115. doi:10.1002/jgt.10128

