American Journal of Computational Mathematics
Vol.04 No.04(2014), Article ID:50198,10 pages
10.4236/ajcm.2014.44032
A New Eighth Order Implicit Block Algorithms for the Direct Solution of Second Order Ordinary Differential Equations
Ademola M. Badmus
Department of Mathematics, Nigerian Defence Academy, Kaduna, Nigeria
Email: ademolabadmus@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 August 2014; revised 11 September 2014; accepted 19 September 2014
ABSTRACT
This paper focuses on derivation of a uniform order 8 implicit block method for the direct solution of general second order differential equations through continuous coefficients of Linear Multi- step Method (LMM). The continuous formulation and its first derivatives were evaluated at some selected grid and off grid points to obtain our proposed method. The superiority of the method over the existing methods is established numerically.
Keywords:
Uniform Order, Second Order Initial Value Problem, Implicit Block Algorithms, Zero Stable

1. Introduction
In the past, efforts have been made by many researchers to develop an efficient algorithm for solving second order differential equations of the form
 (1.0)
(1.0)
directly through the interpolation and collocation points (see [1] -[4] to mention a few). Since many numerical techniques are available for the solution of higher order initial value problems (IVPs) and these techniques depend on many factors such as speed of convergence, computational expenses, data storage requirement and accuracy.
This paper aimed to address all these factors in the process of derivation and the implementation of this new method. Seven-point solutions are obtained from the block at once which speed up the computational processes; the method is self-starting and we obtained better accuracy over the existing methods.
The Equation (1.0) where f is a continuous function, is conventionally solved by first reducing it to a system of first order differential equations and then applying the various first order methods available for their solutions. This approach is extensively discussed and established by some of the following researchers such as ([5] [6] ). Also [7] [8] and [9] showed that this approach was associated with certain drawbacks. Due to the dimension of the problem after it has been reduced to a system of first order ordinary differential equations (ODEs), also the reduced systems of ODEs are not well posed unlike the given problem. The approach wastes a lot of computer time and human efforts, hence there is a great need to develop new and efficient algorithms to handle problem (1.0) directly without any reduction to its equivalent system of first order ODEs.
Several authors have also solved problem (1.0) through predictor corrector mode (PC) of implementations; among them are [10] and [11] . Although the implementation of the methods in a PC mode yields good accuracy, the approach is more costly to implement, for instance PC routines are very complicated to write, since they require special techniques for supplying starting values and also predicting all the off grid points present in the method which leads to longer computer time and human efforts to handle their approach.
In our new algorithms, we take great advantage of this approach by exploring its continuous formulation nature to obtain some discrete schemes when evaluated at some
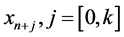 to form our block method; schemes are equally obtained from the derivative of the continuous formula.
to form our block method; schemes are equally obtained from the derivative of the continuous formula.
Definition 1.0
A linear multi-step method is said to be zero-stable if the roots
 of the first characteristic polynomials
of the first characteristic polynomials
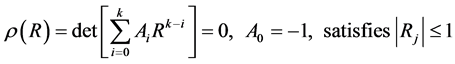 .
.
If one of the roots is +1, we call this the principal root of
 (see [12] ).
(see [12] ).
Definition 1.1
A linear multi-step method
 . (1.2)
. (1.2)
We associate the linear differential operator
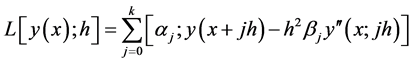 (1.3)
(1.3)
where
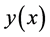 is an arbitrary function, continuity differentiable on
is an arbitrary function, continuity differentiable on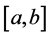 .
.
Expanding the test function
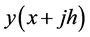 as Taylor series about x and collecting terms gives
as Taylor series about x and collecting terms gives
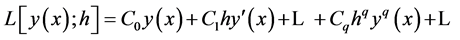
where
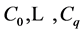 are constants.
are constants.
A simple calculation yields the following formulae for the constants
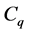 in terms of the coefficients
in terms of the coefficients
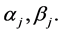

Hence, we say that the method has order P if
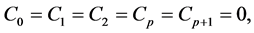 but
but



2. Theory of Block Methods for Second Order Initial Value Problems
Within the r-vectors




The S block r-point methods for
are given by the matrix finite difference equation.

where



The block scheme (2.0) is explicit if the coefficient matrix

Let

be respectively the theoretical solution to Equation (1.0) (see [12] [13] ).
3. Specification of the Method
We consider a power series of single variables x in the form

which is used as the basis or trial function to produce our approximate solution to (1.0) as



where

Equation (3.3) is collocated at



thod k = 3 and specifically gives the following system of non linear equations of the form h


The continuous formulation of the method will be of the form

When using Maple 17 mathematical software to obtain the values of


Evaluating (3.7) at



Equation (3.8) is our proposed uniform eighth order block method with the error constants exhibited in Table 1.
Table 1. Order and error constants of schemes (3.8).
Also the first derivative of (3.7) is evaluated at


Equation (3.9) has the following order and error constants in Table 2.
4. Implementation Strategies
Equation (3.9) is substituted in Equation (3.8) when applying to Equation (1.0) directly at

produces solutions at the point






Table 2. Order and error constants of schemes (3.9).
for





certain their degree of accuracy with the existing methods.
5. Numerical Experiments
Three numerical experiments of two linear and one non linear problem were used to ascertain the efficiency of the method.
Example 1

Theoretical solution is
Example 2

Theoretical solution is
Example 3

No theoretical solution.
6. Conclusion
We want to re-emphasize the claim made by [14] for first order schemes that when the derived schemes for various values of k are of the same order the block scheme gotten from the minimal value of k performed excellently well and compared favourably with the exact solutions. This has also been established for second order schemes derived from various values of k which are of the same order with three different numerical experiments tested (see Figure 1, Figure 2 and Figure 3).
Table 3 and Table 4 also display the numerical result of problem 1 and absolute errors by using various block methods of k = 4, k = 5 together with the new block method at k = 3. Table 5 and Table 6 display the numerical result of problem 2 and absolute errors by using various block methods of k = 4, k = 5 together with the new block method at k = 3.
Table 7 displays the approximate solution of example 3 with block methods of k = 4, k = 5 together with the
Figure 1. Error graph of problem 1.
Figure 2. Error graph of problem 2.
Figure 3. Error graph of problem 3.
Table 3. Table of result for example 1.
Table 4. Absolute error of problem 1.
Table 5. Table of result for example 2.
Table 6. Absolute error of problem 2.
Table 7. Table of result for example 3.
Table 8. Global error of problem 3.
Where


new block method at k = 3 while Table 8 is the global or approximate error of problem 3, since this problem has no theoretical solution.
References
- Yahaya, Y.A. and Badmus, A.M. (2009) A Class of Collocation Methods for General Second Order Ordinary Differential Equations. African Journal of Mathematics and Computer Science Research, 2, 69-72.
- Badmus, A.M. and Ekpenyong, F.E. (2013) High Order Block Method for Direct Solution of General Second Order Ordinary Differential Equations. Academy Journal of Science and Engineering, Nigerian Defence Academy Kaduna, 7, 36-42.
- Badmus, A.M. and Yahaya, Y.A. (2009) An Accurate Uniform Order 6 Block Method for Direct Solution of General Second Order Ordinary Differential Equations. The Pacific Journal of Science and Technology, 10, 248-254.
- Jator, S.N. (2007) A Class of Initial Value Methods for Direct Solution of Second Order Initial Value Problems. 4th International Conference of Applied Mathematics and Computing, Plovdiv, 12-18 August 2007.
- Lambert, J.D. (1973) Computational Methods in Ordinary Differential Equations. John Wiley and Sons, New York, 278.
- Lambert, J.D. (1991) Numerical Method for Ordinary Differential Systems. John Wiley and Sons, New York, 293.
- Awoyemi, D.O. (1999) A Class of Continuous Method for General Second Order IVPs in Ordinary Differential Equations. International Journal of Computer Mathematics, 72, 29-37. http://dx.doi.org/10.1080/00207169908804832
- Jator, S.N. (2001) Improvements in Adams-Moulton Methods for the First Initial Value Problems. Journal of the Tennessee Academy of Science, 76, 57-60.
- Onumanyi, P., Awoyemi, D.O., Jator, S.N. and Siriseria, U.W. (1994) New Linear Multistep Methods with Continuous Coefficients for First Order IVPs. Journal of Nigeria Mathematics Society, 13, 37-51.
- Awoyemi, D.O. (2003) A P-Stable Linear Multistep Method for Direct Solution of General Third Order Ordinary Differential Equation. International Journal of Computer Mathematics, 80, 987-993. http://dx.doi.org/10.1080/0020716031000079572
- Vigo-Angular, J. and Ramos, H. (2006) Variable Step-Size Implementation of Multi-Step Methods
. Journal of Computation and Applied Mathematics, 92, 114-131.http://dx.doi.org/10.1016/j.cam.2005.04.043
- Fatunla, S.O. (1991) Block Method for Second Order Differential Equations. International Journal of Computer Mathematics, 41, 55-63. http://dx.doi.org/10.1080/00207169108804026
- Yahaya, Y.A. (2004) Some Theories and Applications of Continuous LMM for Ordinary Differential Equations. PhD Thesis (Unpublished), University of Jos, Nigeria.
- Badmus, A.M. and Mshelia, D.W. (2012) Uniform Order Zero Stable k-Step Block Methods for Initial Value Problems of Ordinary Differential Equations. Journal of Nigerian Association of Mathematical Physics, 20, 65-74.
- Badmus, A.M. (2014) An Efficient Seven Point Block Method for Direct Solution of General Second Order Ordinary Differential Equations
. British Journal of Mathematics and Computer Science, 4, 2840-2852.http://dx.doi.org/10.9734/BJMCS/2014/6749













 . Journal of Computation and Applied Mathematics, 92, 114-131.
. Journal of Computation and Applied Mathematics, 92, 114-131. . British Journal of Mathematics and Computer Science, 4, 2840-2852.
. British Journal of Mathematics and Computer Science, 4, 2840-2852.