ABSTRACT

A model for the definition of electrical Power is presented, which retrieves the concepts of homomorphism from the geometrical tensor approximation at the wavelet approach. Their definition here is nevertheless different in that it considers both tensor algebra and wavelet operators, solving thus most of the problems usually associated with the numerical methods.

1. Introduction

Traditionally, the development of pattern recognition is known as “power quality” in power systems from electrical engineering point of view. In this way many works has been published in the last decades [1-7]. In the major approaches isfocalized to see how the perturbation affect the normal operation of the power systems. In power distribution networks, particular aspects as the feeder has been directed in order to the optimal power transfer. It is necessary proposed a new definition and methodology for solver the problem of the optimal power transfer. This work is fundamental supporting in the aspect to see a new power definition from an analytical point of view.

Algebra, functional analyses and geometry are the building blocks for the construction of the language engineers currently want to use [7-10]. The basic principles on which this proposed theory is developed are founded on these three pillars. The postulates are:

1) Electromagnetic energy, intended as intermediary, is continuous in systems of rational energy usage.

2) Two elements, v and i are defined in the system. These elements comply with the terms of a vector space, with inner product and norm induced by this product, and the space H (Hilbert space) generated by those components is complete. In other words, any Cauchy sequence in H, converges to an element in H.

3) There are orthonormal sets in these Hilbert spaces, which form bases andcreate space. Additionally, the Fourier analysis can be applied.

Hypothesis 1:

The implementation of this system under a new algebraic structure will keep the previous assumptions in the combination v and i, because of the principle of energy conservation. The algebraic structure to be used is the dyadic or tensor product introduced in [11] and [12].

Hypothesis 2:

The operator to be applied will have a homomorphous behavior. The properties of the generated space

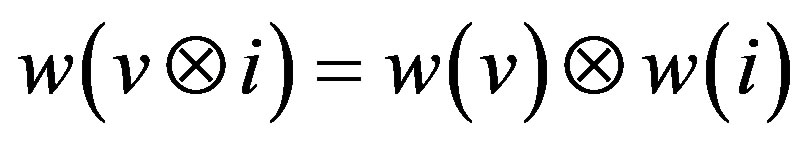continue to be of Hilberian space.

The conditions of these hypotheses must be framed within the analysis of matrix functions in several variables.

2. Evaluation of the First Hypothesis

2.1. Instantaneous Power Tensor Theory

The proposed method is based on the definition of an evolutionary expression of instantaneous power, called “instantaneous power tensor” [13], in order to geometrically interpret the dynamic behavior of electromagnetic phenomena, analogous to studies of deformation in the mechanics of solids. Therefore, the goal proposed is to obtain a single expression containing the two components of the instantaneous power (active and reactive). Therefore, using the dyadic or tensor product the proposed expression is as follows:

(1)

where Ã_ij is the instantaneous power tensor and subscript t refers to the vector transpose. On the other hand, a multiphase electrical network was defined as one n-phase and m-wire power system related to the dimension of vector space, where voltage vector and current vector were defined assuming that, R¹ is the single-phase system, R² is the two-phase system with two-wire or three-wire, R³ is the three-phase system with three-wire or four-wire and Rⁿ is the multiphase system with n-phase and mwire.

Therefore, in a system of n-phase and m-wire, where the instantaneous vectors of voltage and current are expressed as:

(2)

Then, the instantaneous power tensor in Rⁿ is equal to:

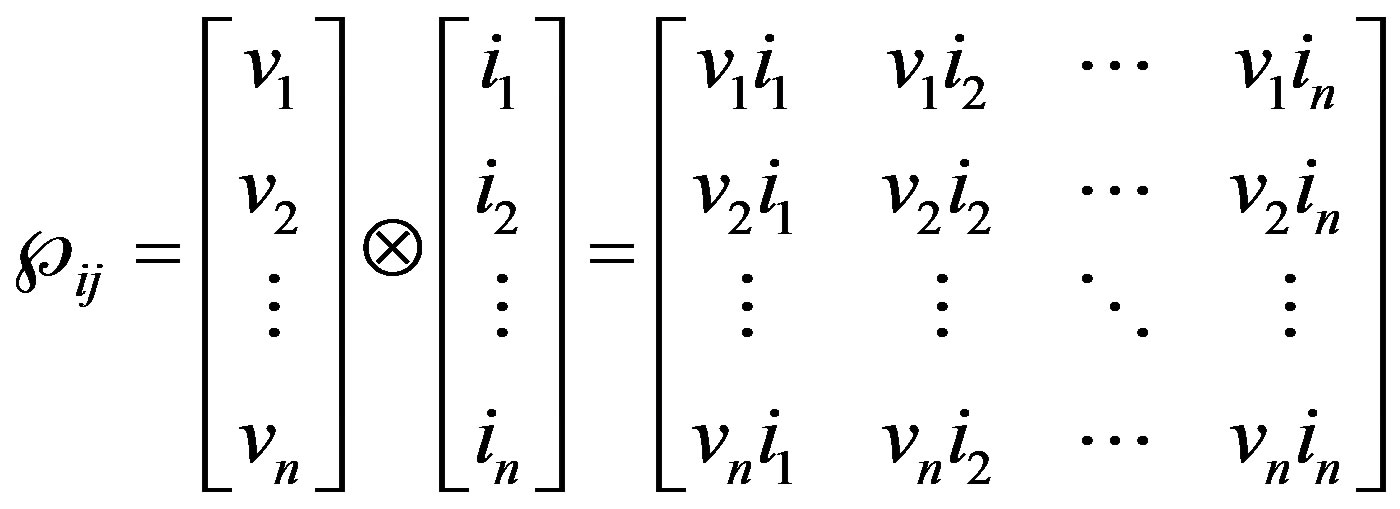(3)

Moreover, in a system of three-phase and three-wire or four-wire, where the phases are identified by a-b-c, the instantaneous power tensor in R³ is expressed as:

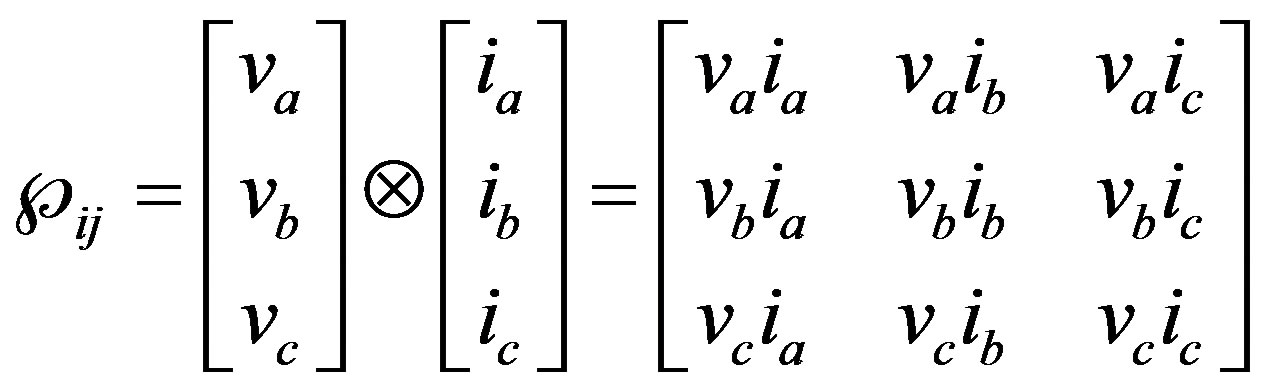(4)

when n = 1, it is the case of a single phase system, and the instantaneous values of voltage and current are scalars. Therefore, according to the traditional concept of instantaneous power in single phase systems the instanttaneous power tensor in R¹ is equal to:

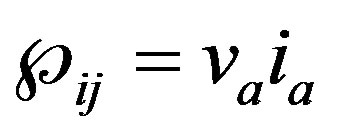(5)

2.2. Orthogonal Decomposition of the Current Vector

According to (1):

(6)

This expression implies that the current vector can be obtained from the definition of instantaneous power tensor as follows:

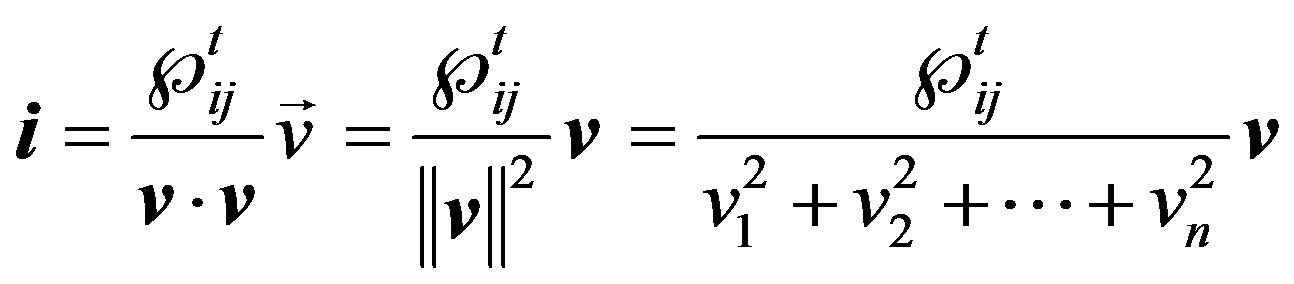(7)

such that, 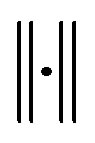denotes the Euclidean norm. Replacing (6) in (7) the current vector can be expressed by,

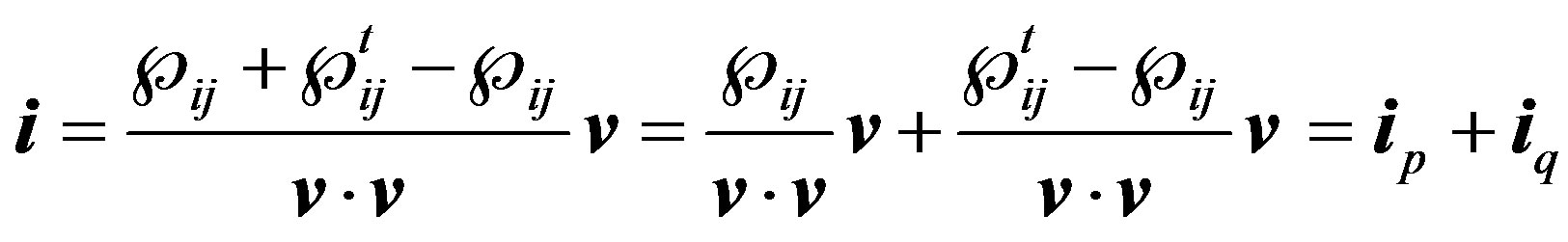(8)

where, is the instantaneous active current vector:

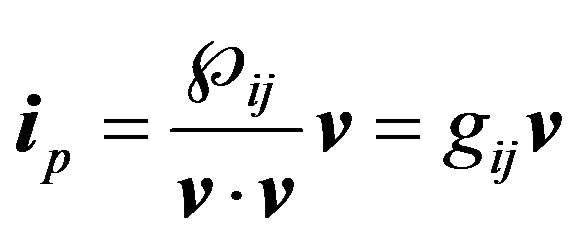(9)

and is the instantaneous reactive current vector:

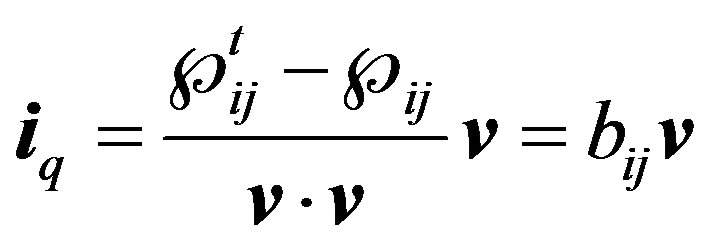(10)

In (9) g_ij is the instantaneous conductance tensor:

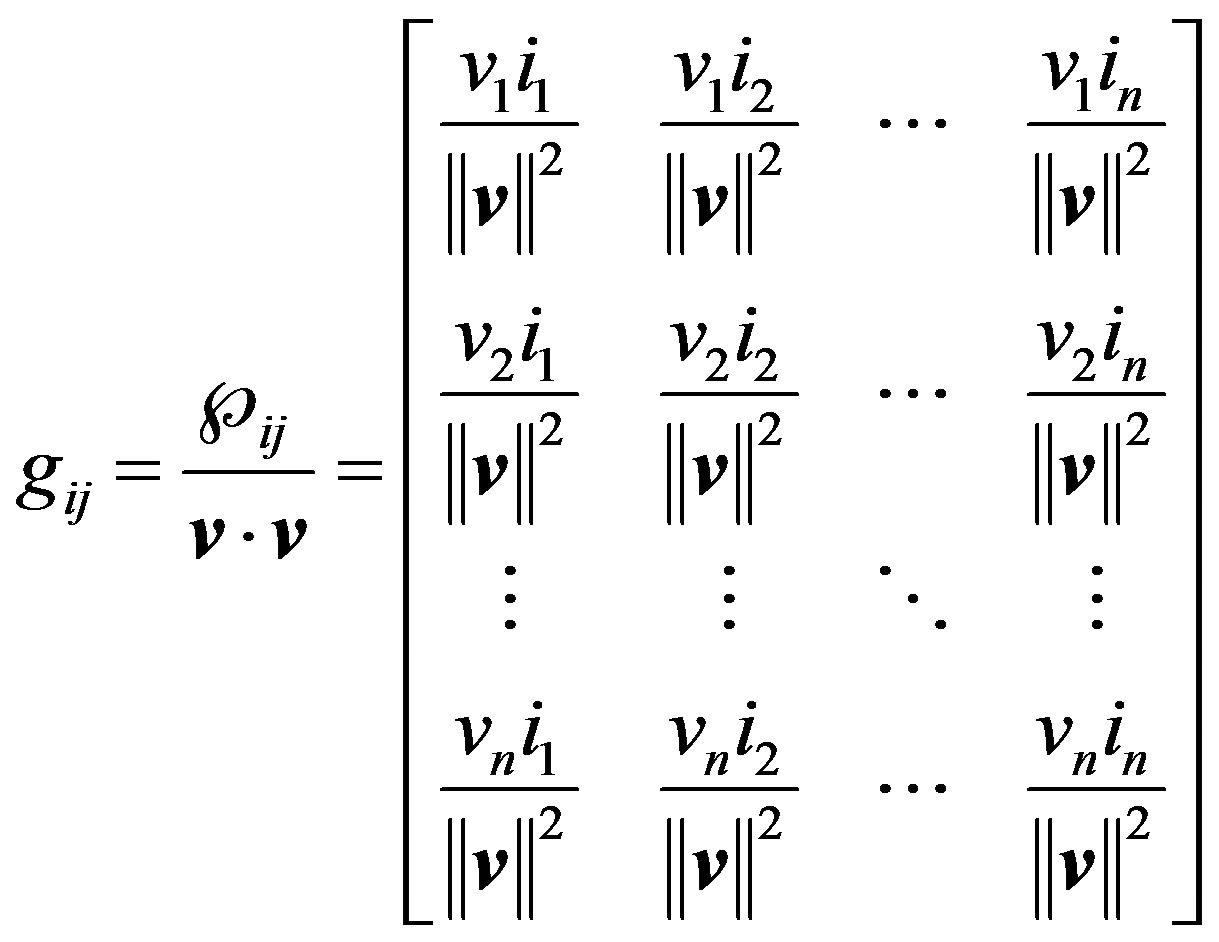(11)

and in (10) b_ij is the instantaneous susceptance tensor:

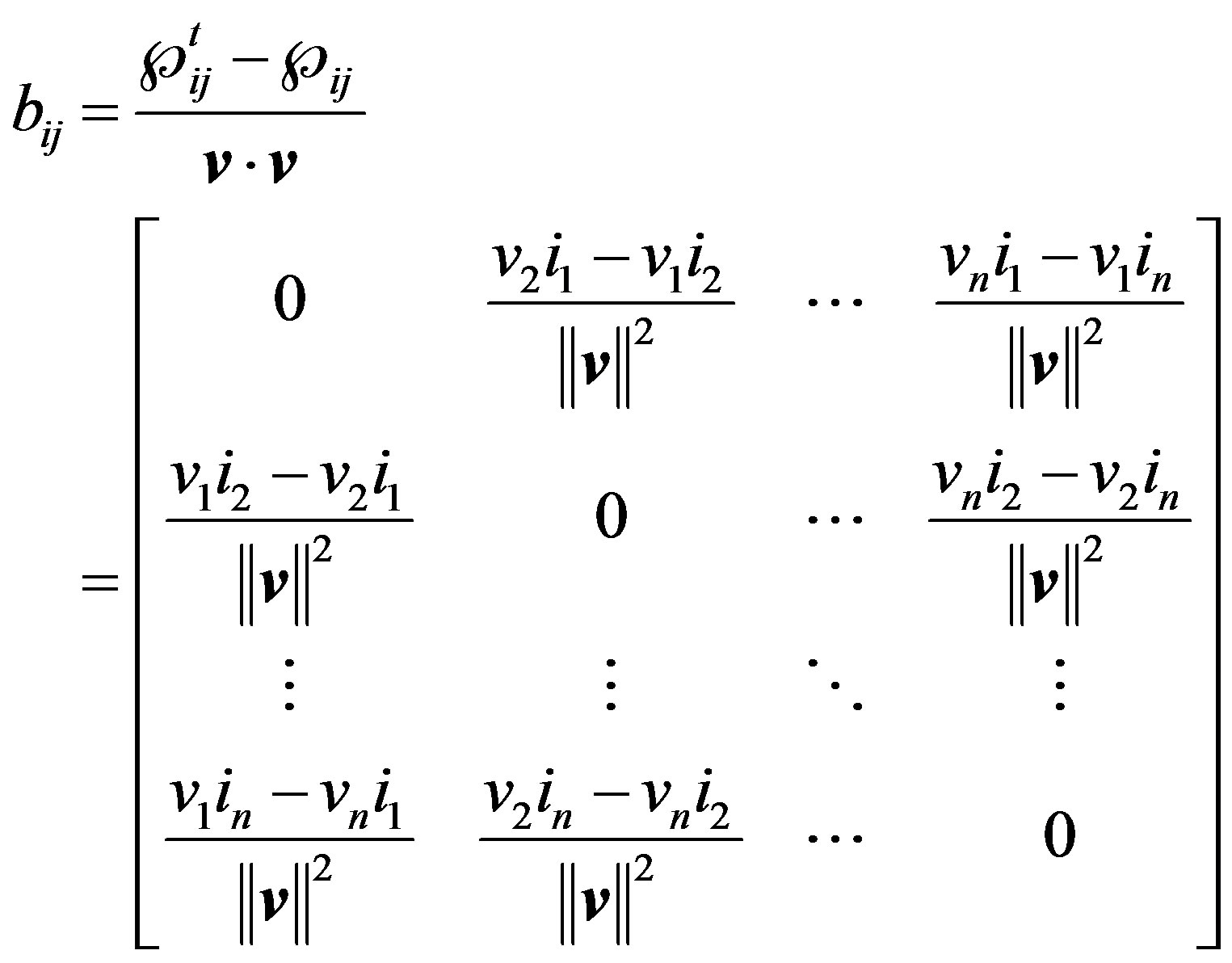(12)

Moreover, the decomposition of the instantaneous current vector is characterized by:

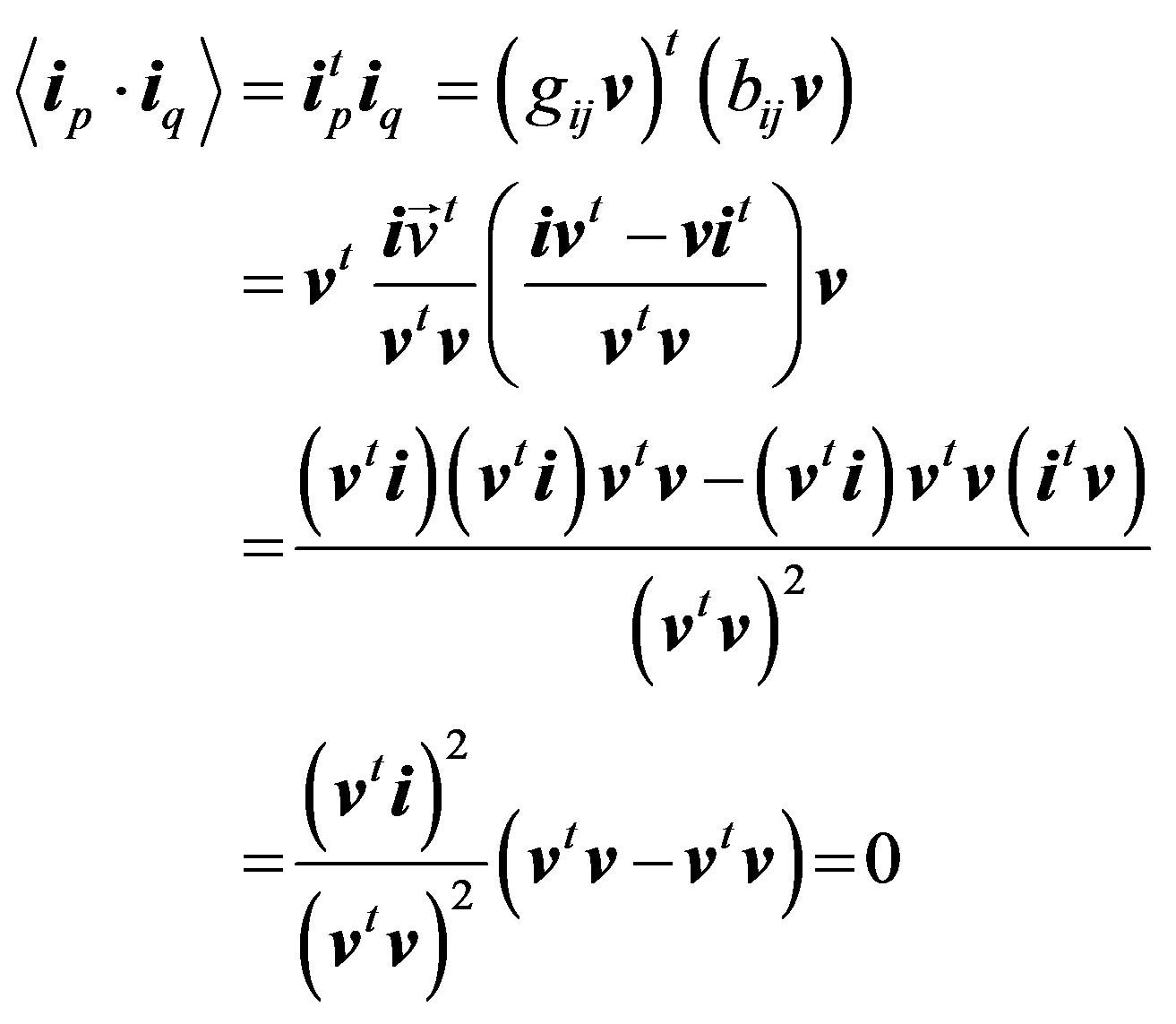(13)

such that,

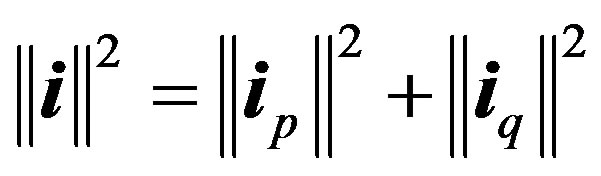(14)

2.3. Orthogonal Decomposition of the Power Tensor

The decomposition of the instantaneous power tensor is obtained by applying the tensor product of the voltage vector on (8), thus:

(15)

Here the first term is the instantaneous active power tensor:

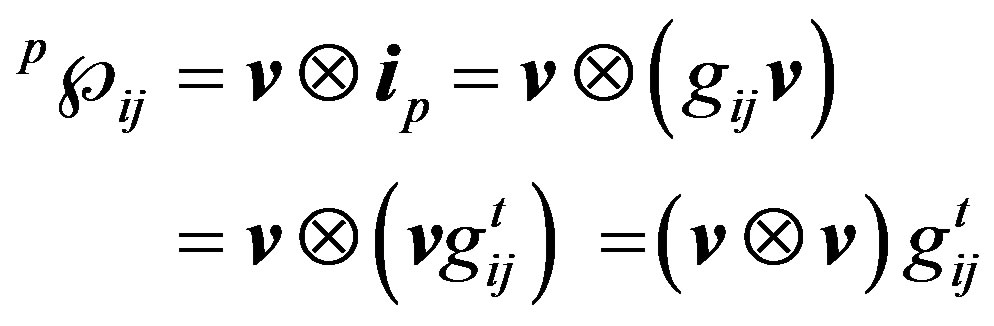(16)

and the second term is the instantaneous reactive power tensor:

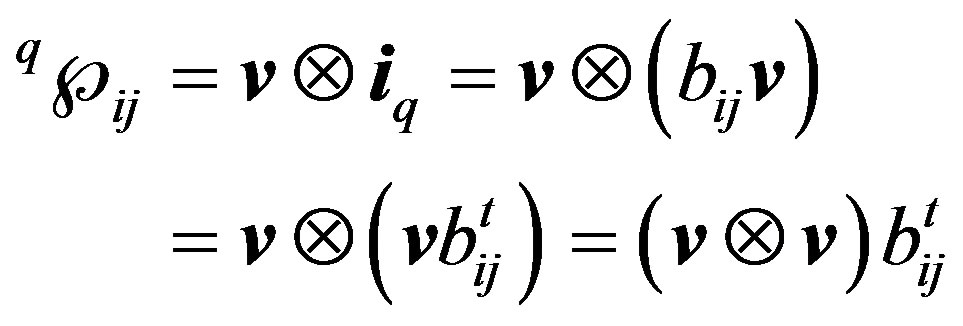(17)

Consequently,

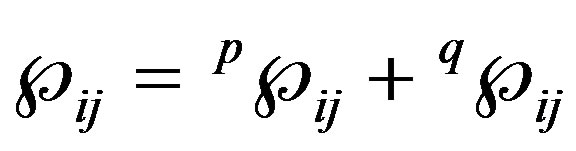(18)

Moreover, (18) satisfies the orthogonality concept, in other words,

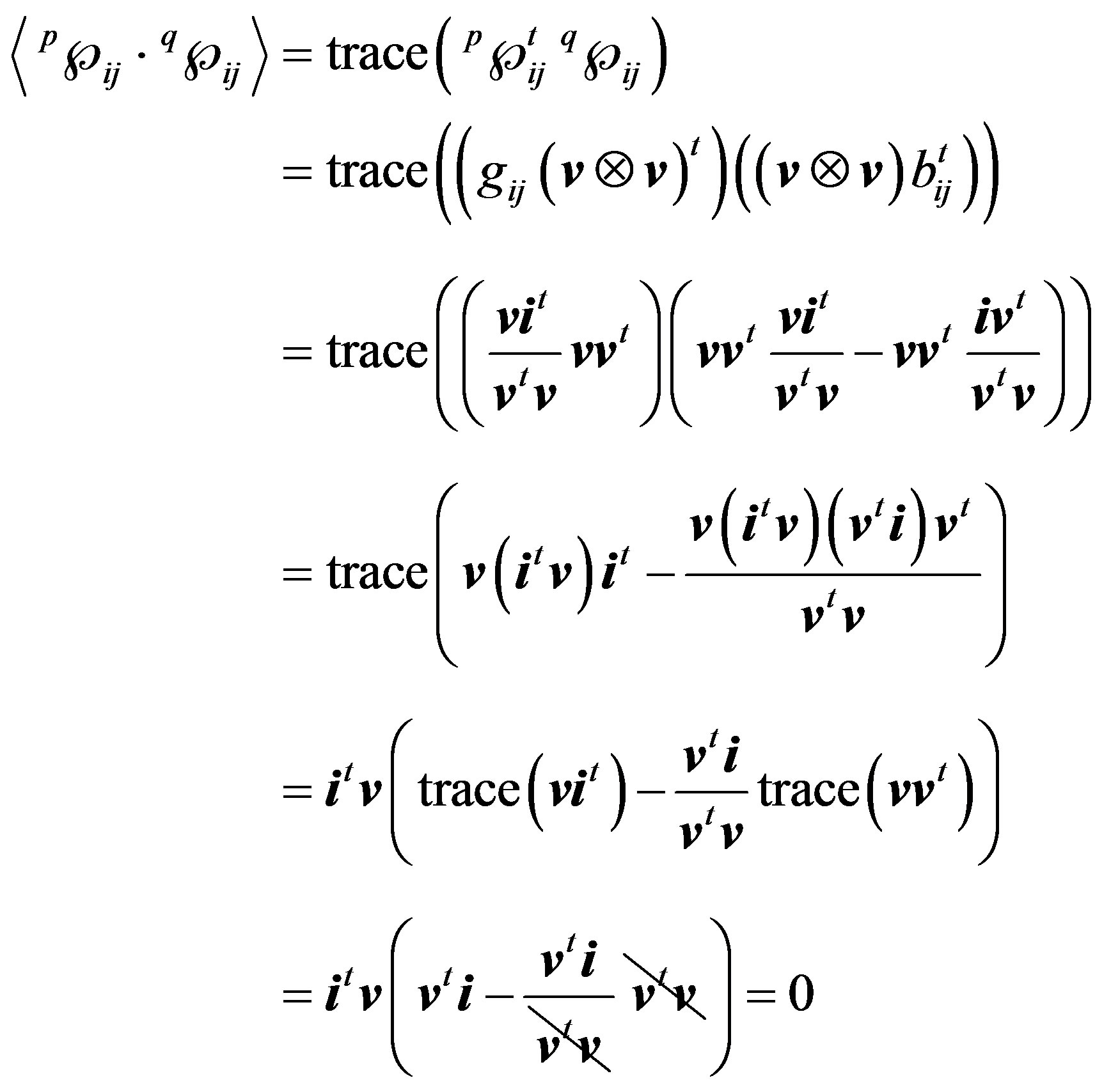(19)

Therefore, it holds that:

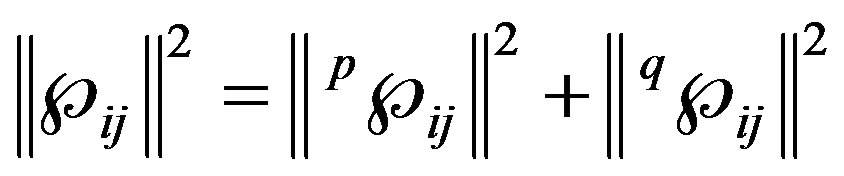(20)

Such that, 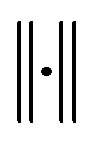denotes the norm of the system. In other words, the space generated by the operation is a normed space with norm induced by the inner product, thus the first hypothesis is proved.

3. Evaluation of the Second Hypothesis

Continuous Wavelet Transform in Several Variables

In [14] shows an intuitive approach to the continuous wavelet transform in several variables. The general formulations are shown below.

Considering a family of matrix functions obtained by scale changes and translations of a wave matrix called “mother wave” formed by a set of systems of one-dimensional wavelets:,

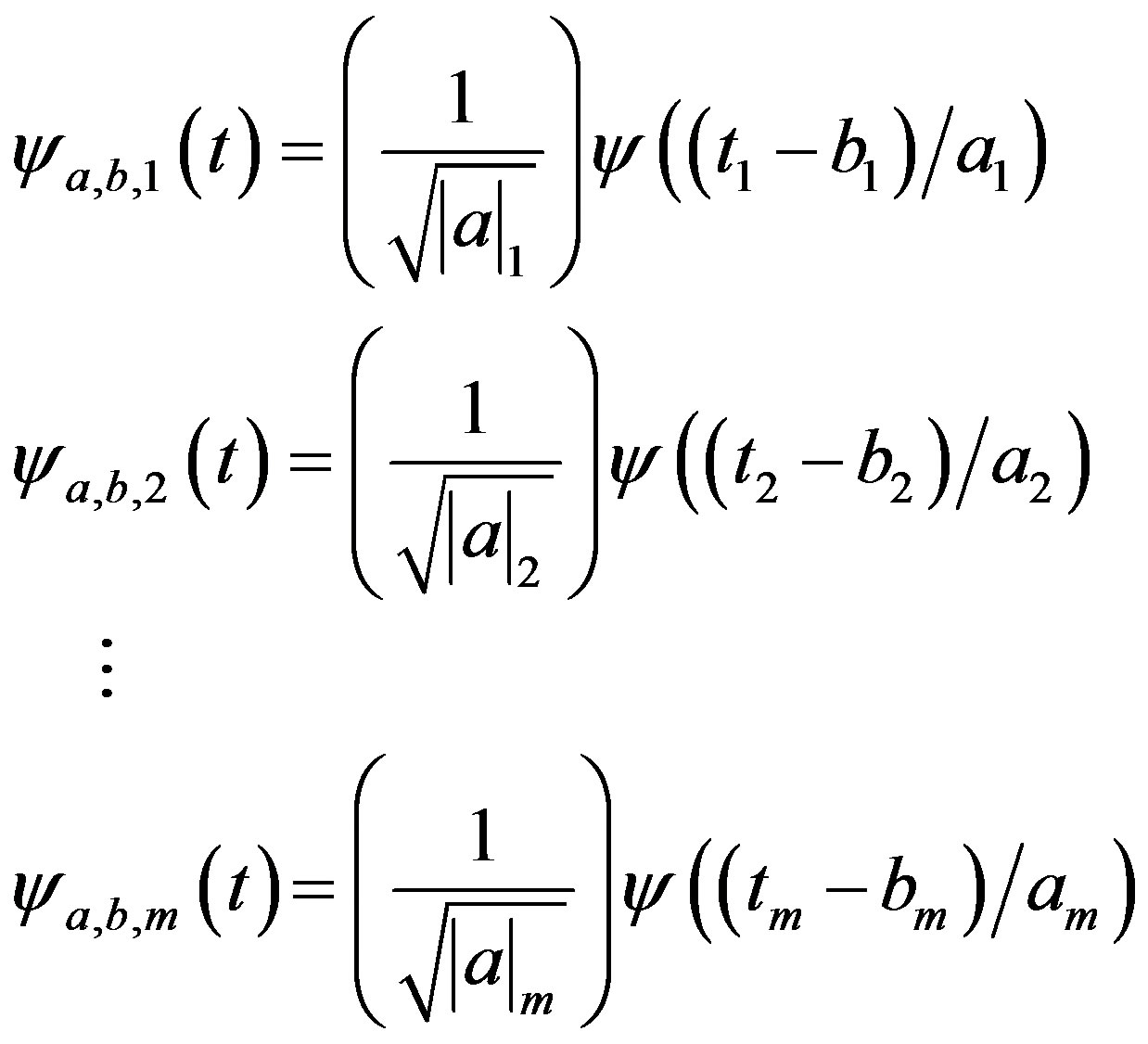(21)

where: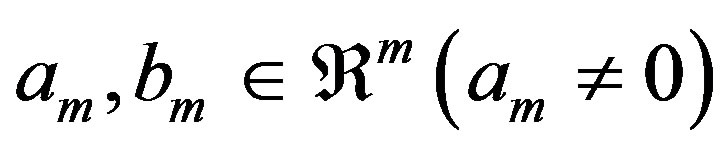. For normalization:

(22)

where m is the dimension of body. It is assumed that the one-dimensional function satisfies the admissibility condition if:

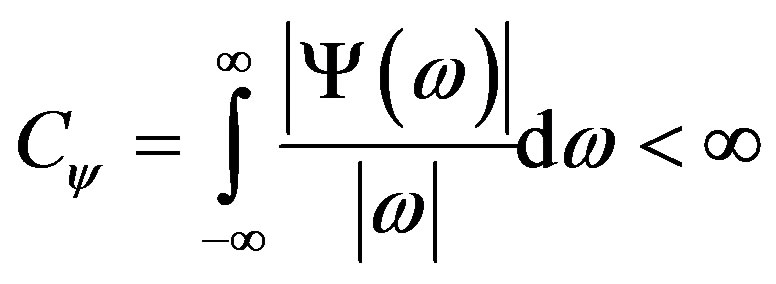(23)

where is the Fourier transform of.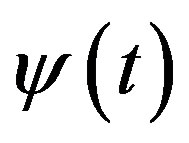

In practice, the wave represented in the frequency frame falls so fast that the admissibility condition is reduced to 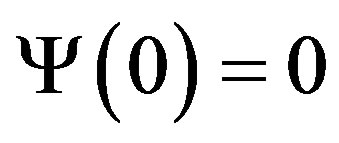or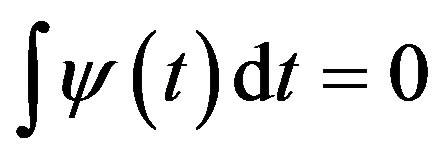. Therefore, To normalize the wavelet so its energy turns unitary implies {XE “eneenergía”}

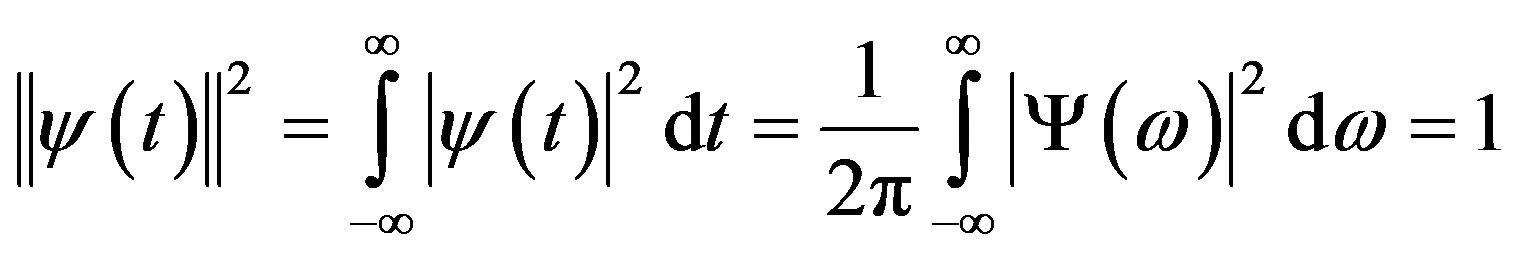(24)

Thus, an additional result will be:

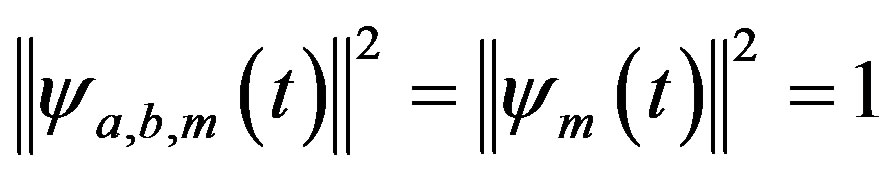(25)

In other words the admissibility condition will have a structure.

Definition 1:

Since 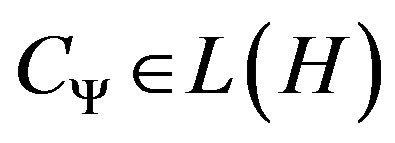an operator of a Hilbert space, it can be said that 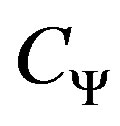complies with the following properties:

1) Hermitian.

2) Unitary.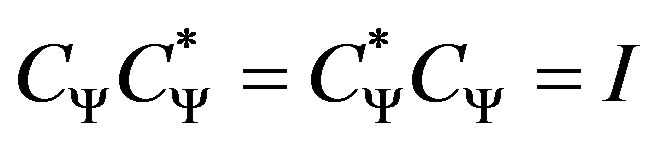

3) Positive definite.

4) Invertible.

Definition 2:

The continuous wavelet transform of a function in several variables, 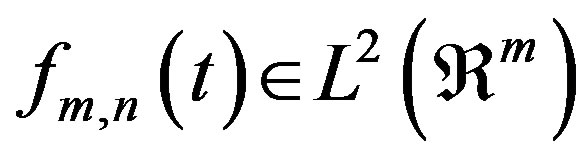(where 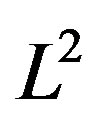is the space of square integrable functions) is defined as:

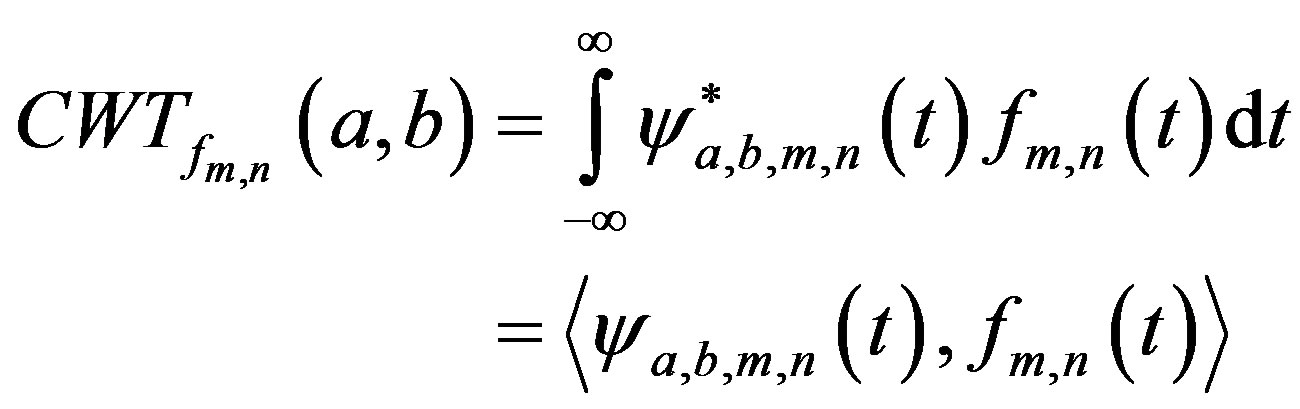(26)

And the question that arises is: is the wavelet operator isomorphic? Following it will be shown how this is possible.

Proposition 1:

Given the continuous wavelet transform

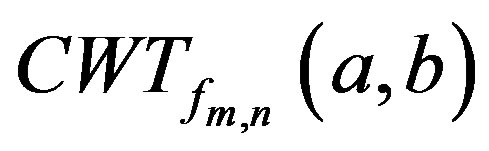of a function 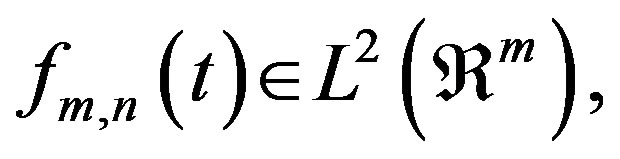the function 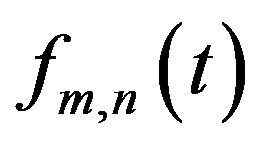might be reconstructed by:

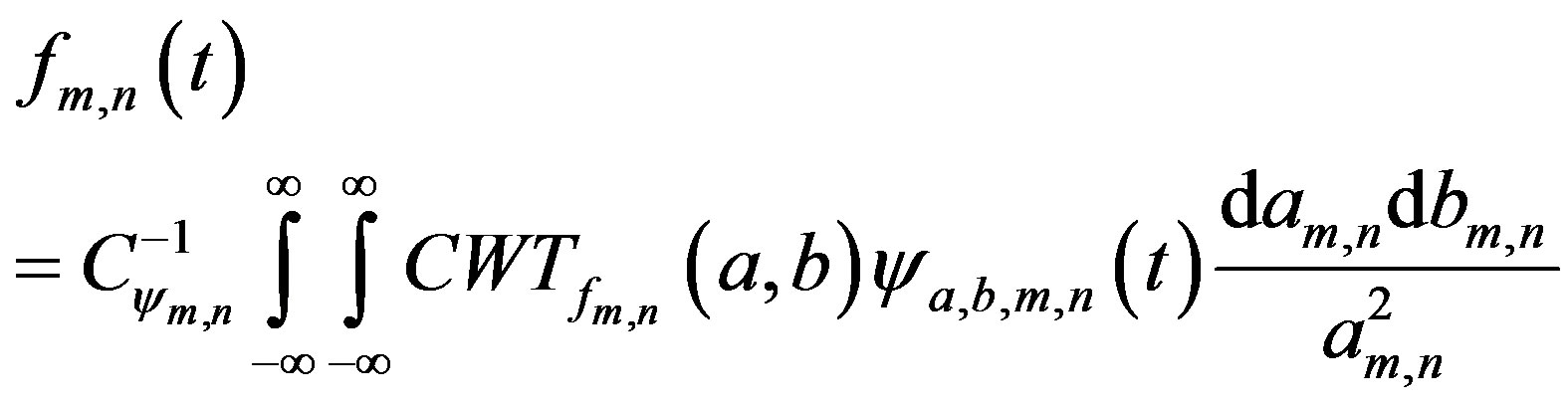(27)

Given the space of functions and the measurement in question, this integration is interpreted as Lebesgue.

Proof:

To simplify the proof was assumed that, just as 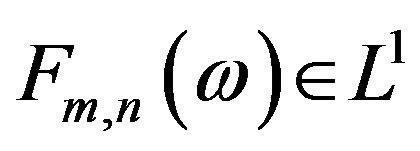(or 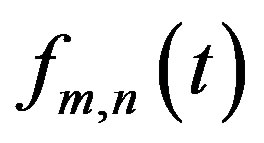continues). First 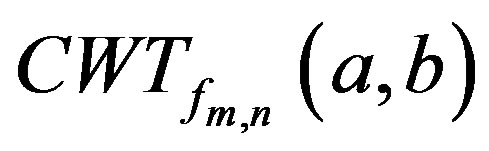is expressed in terms of Fourier transform of the wavelet and the signal.

Note that the Fourier transform of 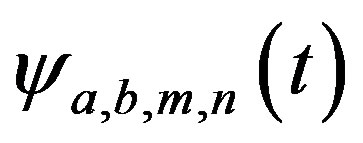is:

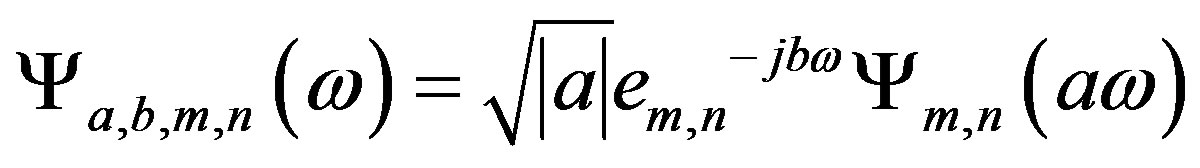(28)

This is the wavelet element m, n of the wavelet matrix operator. According to Parseval equality:

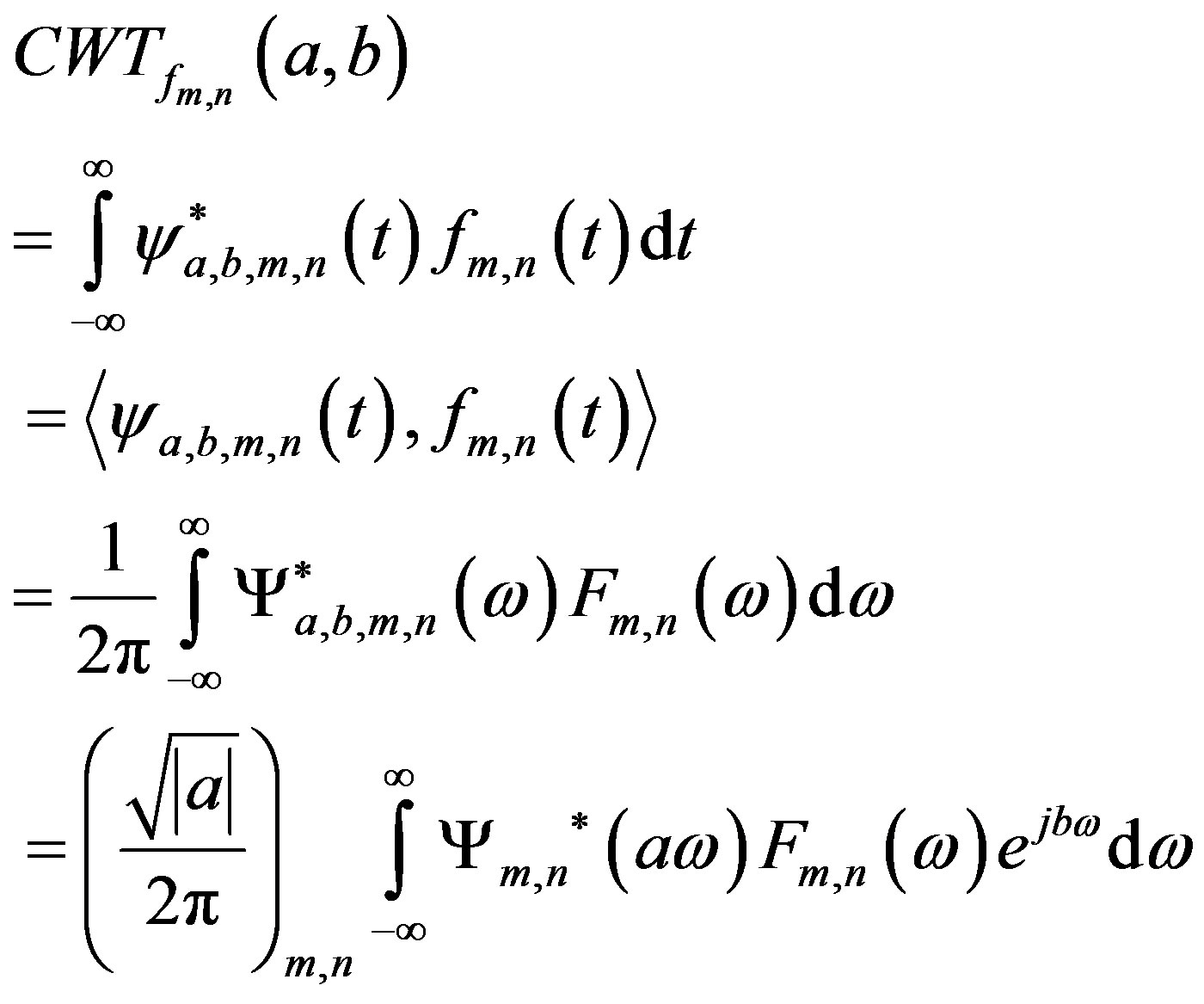(29)

Note that the integral in (29) is proportional to the inverse Fourier transform of 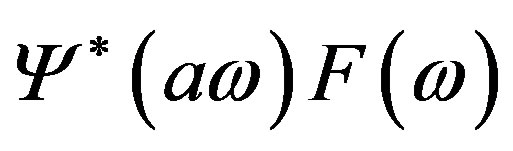in each of the components of the matrix and it is a function of b. The above mentioned operation is valid, once the system is understood as an operator that keeps it in the same space.

Be the element m,n of the matrix J:

(30)

replacing (29) in (30):

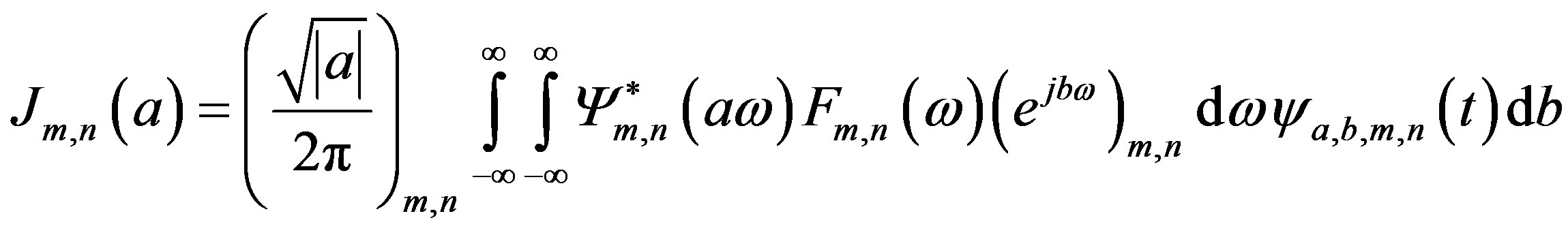(31)

Applying Fubini’s theorem to each component of the matrix J [15]:

(32)

Substituting for each component of the matrix 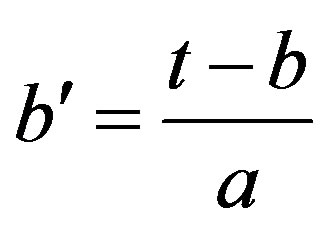in the second integral, gives:

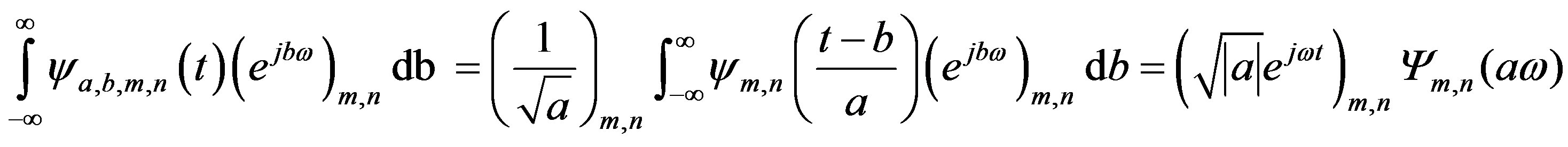(33)

And replacing this result in (32), gives:

(34)

Evaluating (29) regarding variable a:

(35)

Given the restrictions imposed on y 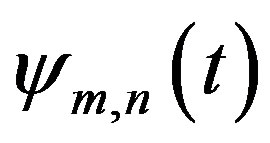the order of integration can be changed by applying Fubini’s theorem and making the change of variable gives:

(36)

This element m,n of the matrix C_ψ must meet definition 1. This integral is independent of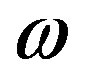, therefore, it can be summarized as:

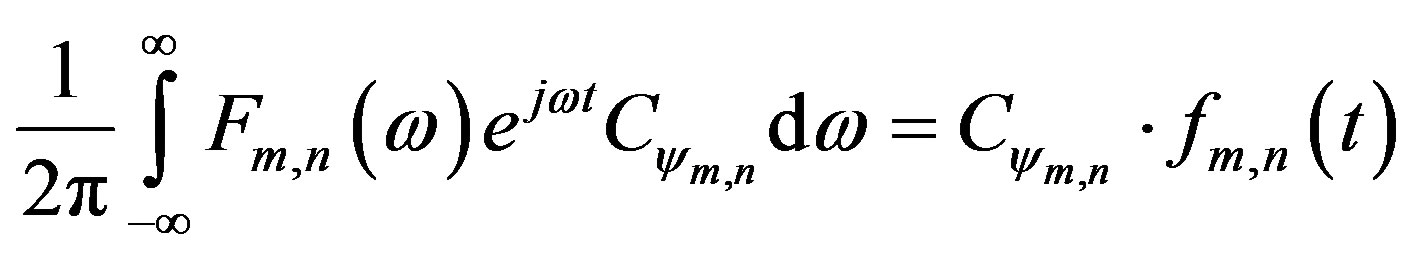(37)

The operator is isomorphic with the condition of admissibility. It might be said that the wavelet transform has the properties of linearity, displacement and scale variance. Following, emphasis will be placed on the property of energy conservation.

Proposition 2:

Given 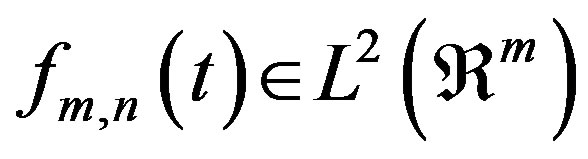and its wavelet transform 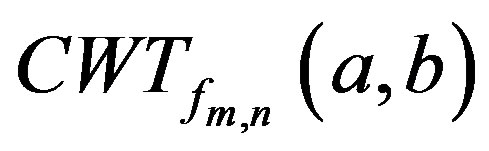{XE “transformada ondita: teorema de conservación de la energía”} {XE “transformada ondita: multiresolucion”} {XE “transformada ondita: función de dos escalas”} {XE “transformada ondita: criterio para selección de onditas”}, the following equality is verified:

(38)

Proof [1]:

From the expression,

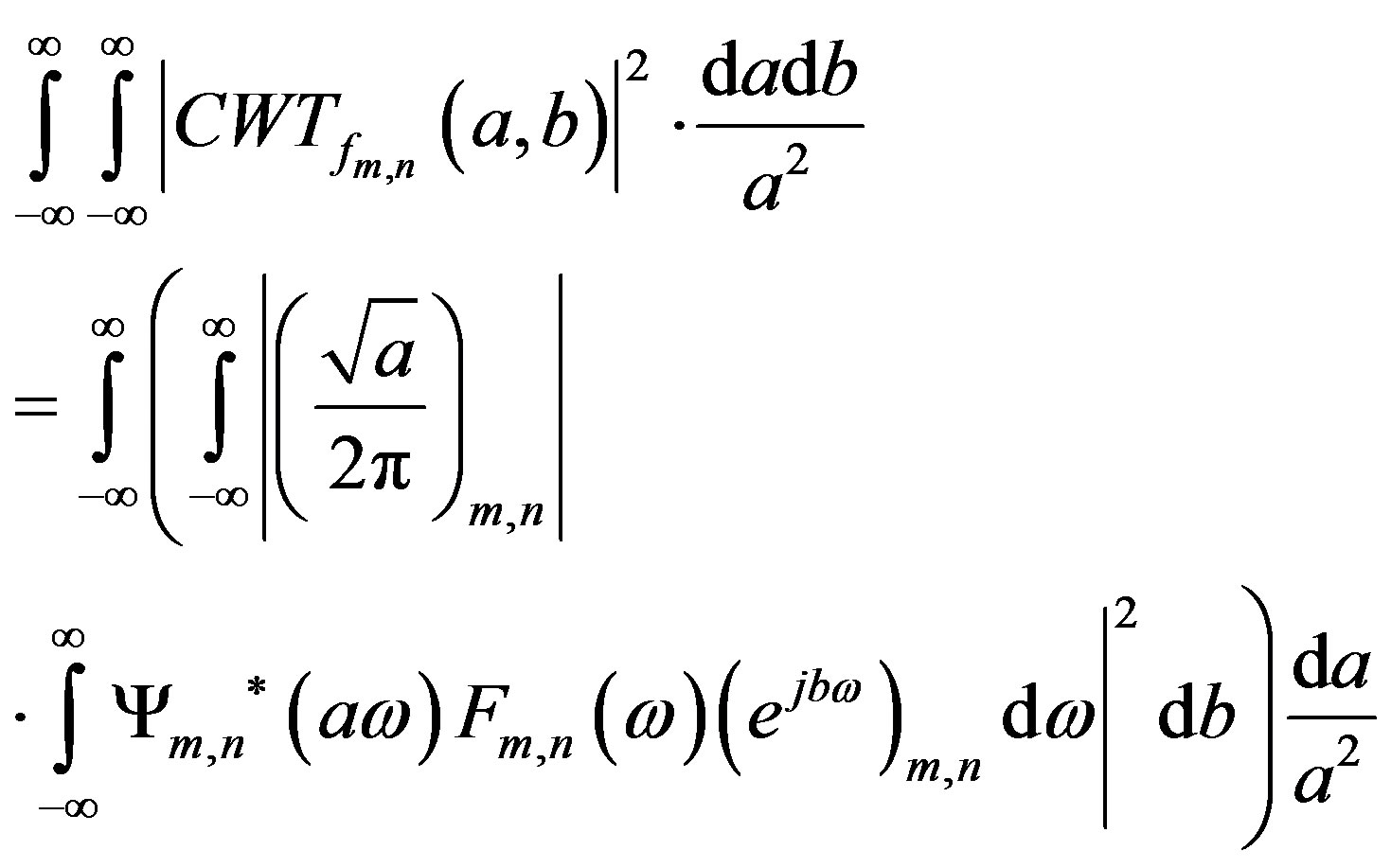(39)

Making the change of function:

(40)

The previous equality might be written as:

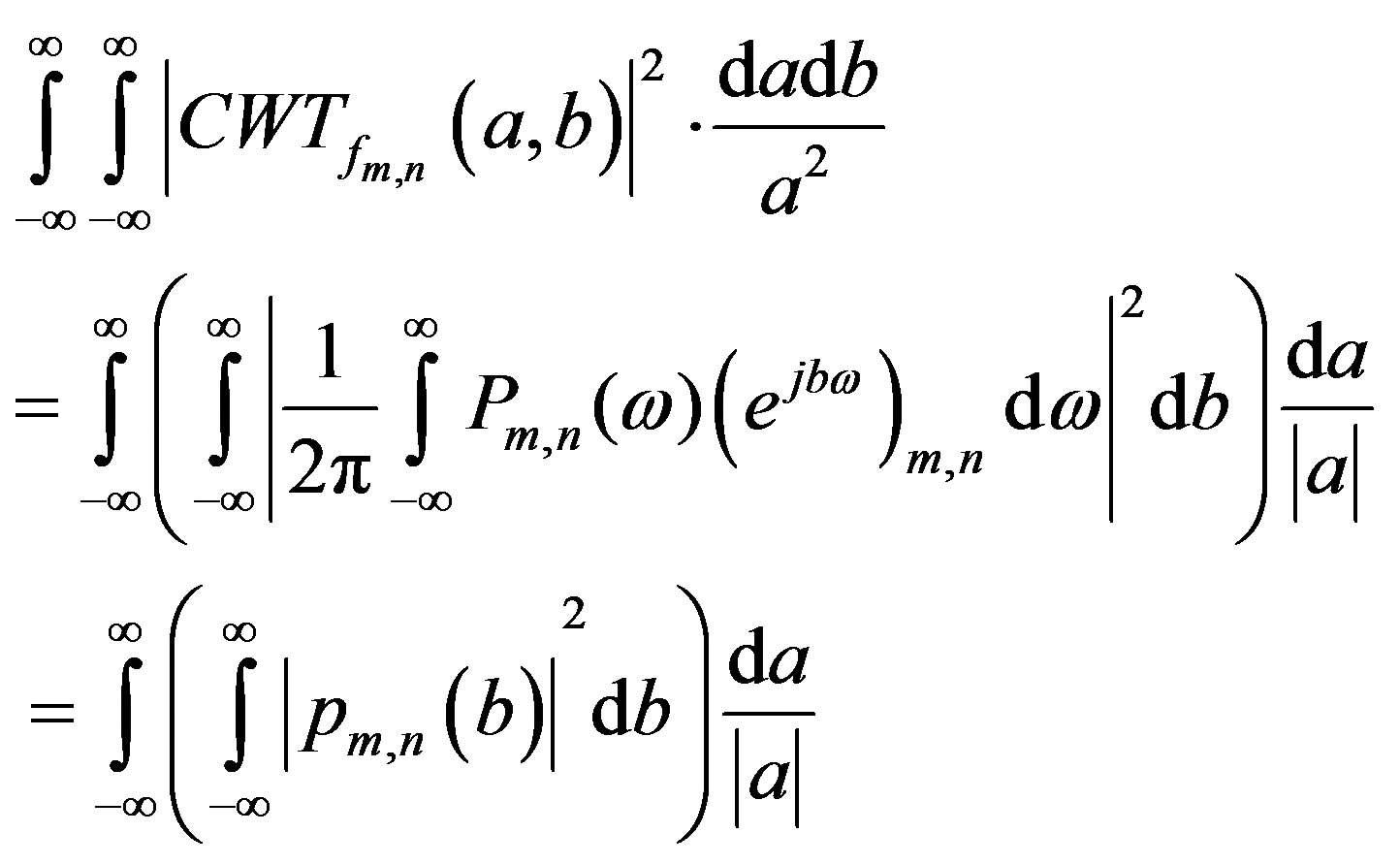(41)

Applying Parseval’s identity:

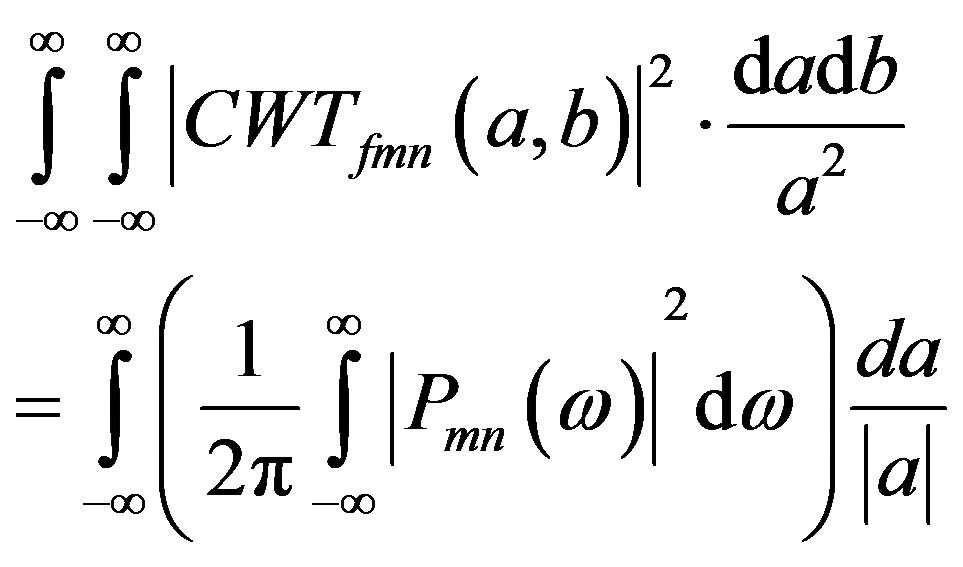
(42)

And replacing (40) in (42), gives:

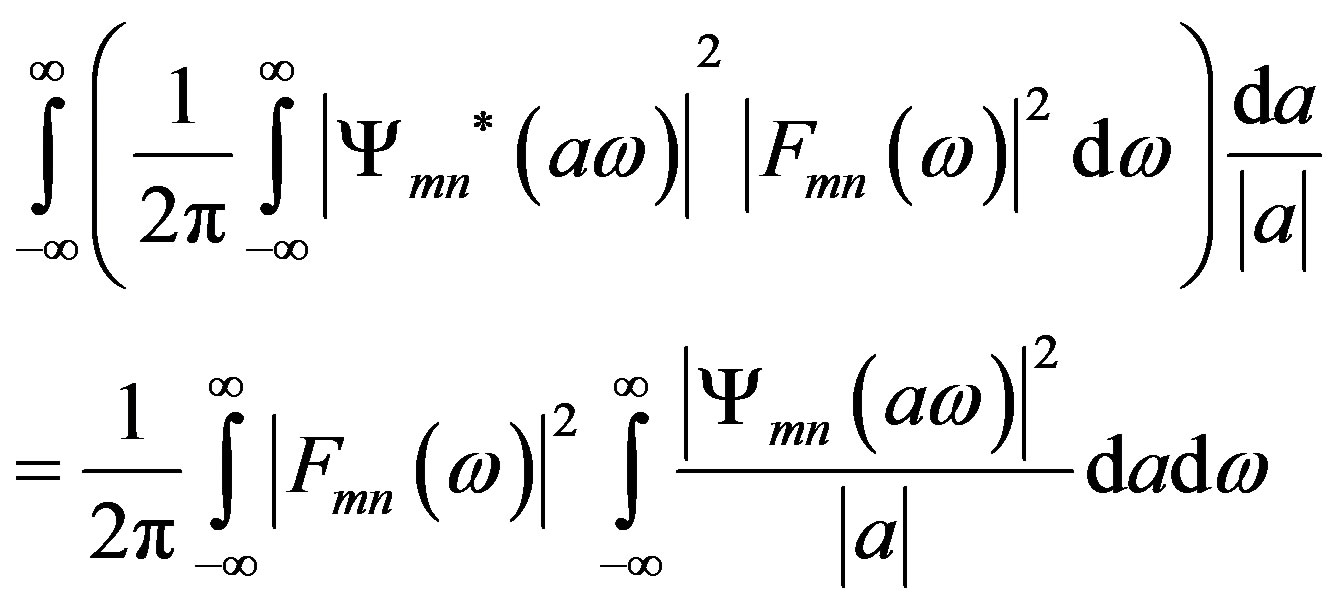(43)

NOTE: The change of the integration is done by Fubini’s and the second integral on the right side is call matrix of admissibility.

Applying once again the Parseval’s equality:

(44)

This is the admissibility condition to be proved, namely the existence of transformable function matrices and with no change of energy. Therefore, it can be deduced that:

(45)

In other words, the wavelet transform shows homomorphism in the presence of the tensor product provided that the conditions of the admissibility matrix are met, and that these conditions are framed within the characteristics in definition 1.

4. Conclusion

Conceptual clarity is essential in the development of a theory that values the characteristics of a system, in particular pattern recognition (Power Quality in electrical systems).Thistheory is based on matrix analyses and functional analyses using algebraic structures, which is a very important ingredient. The aim of this paper is to interpret in light of Engineering, a foundation to evaluate the Instantaneous Power Theory, through the wavelet operator, under the dyadic product structure. This method open the door for obtained a possible way from the analysis of the optimal power systems transfer.

REFERENCES