American Journal of Operations Research
Vol. 2 No. 3 (2012) , Article ID: 22430 , 9 pages DOI:10.4236/ajor.2012.23042
An Effective Routing Algorithm with Chaotic Neurodynamics for Optimizing Communication Networks
1Department of Electrical and Electronic Engineering, Nippon Institute of Technology, Saitama, Japan
2Graduate School of Science and Engineering, Saitama University, Saitama, Japan
Email: tkimura@nit.ac.jp
Received May 9, 2012; revised June 12, 2012; accepted June 25, 2012
Keywords: Chaotic Neurodynamics; Congestion Control; Packet Routing Problems; Complex Networks
ABSTRACT
In communication networks, the most significant impediment to reliable communication between end users is the congestion of packets. Many approaches have been tried to resolve the congestion problem. In this regard, we have proposed a routing algorithm with chaotic neurodynamics. By using a refractory effect, which is the most important effect of chaotic neurons, the routing algorithm shows better performance than the shortest path approach. In addition, we have further improved the routing algorithm by combining information of the shortest paths and the waiting times at adjacent nodes. We confirm that the routing algorithm using chaotic neurodynamics is the most effective approach to alleviate congestion of packets in a communication network. In previous works, the chaotic routing algorithm has been evaluated for ideal communication networks in which every node has the same transmission capability for routing the packets and the same buffer size for storing the packets. To check whether the chaotic routing algorithm is practically applicable, it is important to evaluate its performance under realistic conditions. In 2007, M. Hu et al. proposed a practicable communication network in which the largest storage capacity and processing capability were introduced. Newman et al. proposed scale-free networks with community structures; these networks effectively extract communities from the real complex network using the shortest path betweenness. In addition, the scale-free networks have common structures in real complex networks such as collaboration networks or communication networks. Thus, in this paper, we evaluate the chaotic routing algorithm for communication networks to which realistic conditions are introduced. Owing to the effective alleviation of packets, the proposed routing algorithm shows a higher arrival rate of packets than the conventional routing algorithms. Further, we confirmed that the chaotic routing algorithm can possibly be applied to real communication networks.
1. Introduction
In communication networks, alleviating packet congestion is one of the most significant ways to ensure secure communication between end users. Appropriate transmission protocols are mandatorily used to optimize carried data traffic. However, it has been shown that the shortest path protocol commonly employed in communication networks faces a serious challenge if the data volume continues to increase [1]. Specifically, the shortest path protocol transmits data using only the distance information of the communication network, and the routers with a large number of shortest paths are easily congested. Thus, it is imperative to improve the transmission algorithm in order to ensure reliable communication throughout the network. For this purpose, an understanding of the data flow dynamics of the packets is necessary. Ohira et al. [2] studied the optimal network structure for packet flow in communication networksand they showed the onset of phase transition behavior from free-flow state to congestion state with an increase in the packet creation rate. Arenas et al. [3] analyzed the phase transition behavior for hierarchical branching networks. Zhao et al. [4] studied the dynamics of flowing packets for various network topologies and showed that networks with significant heterogeneous properties inhibited packet congestion.
To allow networks to carry a large volume of data traffic, we need to develop effective routing algorithms that can reduce drastically the congestion in a communication network. Recent works in this regard have been based on two basic ideas. The first one is the selection of paths for transmitting packets based on only local information of the communication network, such as degree information [5,6]. The second idea is to utilize global information such as the shortest distance information of the communication network. Yan et al. [7] proposed a routing algorithm using both the distance information and degree information. Zhang et al. [8] proposed an adaptive routing algorithm based on measurement of the number of packets accumulated on the shortest paths. A routing algorithm with traffic awareness was proposed by Wang et al. [9]. Further, Horiguchi et al. [10] proposed a routing algorithm employing mutually connected neural networks. This method was further improved by a reinforcement learning algorithm [11] and by the incorporation of stochastic effects [12]. Further, Kimura et al., proposed a routing algorithm with memory information [13].
A good routing algorithm transmits packets to their destinations as quickly as possible. The shortest path algorithm is a basic routing algorithm that transmits a packet to its destination along the shortest path to the destination of the packet. If all the nodes in a communication network have high performance, i.e., each node has a large buffer size and simultaneously transmits as many packets as possible, this routing algorithm works well. However, the buffer size and transmission abilities of each node are different in a real communication network. This implies that if one node uses only Dijkstra’s algorithm, packet congestion can easily occur in the real computer network. Thus, it is very important to establish a sophisticated routing algorithm to avoid packet congestion.
To alleviate packet congestion, one possible algorithm involves prohibiting the transmission of a packet to an adjacent node to which the packets just have been transmitted for certain period. On the basis of this approach, we have already proposed a routing algorithm with chaotic neurodynamics [14-20]. Chaotic neurodynamics exhibits a high ability to solve the various combinatorial optimization problems such as traveling salesman problems (TSP) [21,22], quadratic assignment problems [23, 24], motif extraction problems (MEP) [25,26], and vehicle routing problems (VRP) [27,28]. The algorithms that solve these problems use the chaotic dynamics of a chaotic neural network [29] to escape from undesirable local minima. As a result, the efficiency of these algorithms increases. In these chaotic routing algorithms [14-20], a refractory effect, which is an important characteristic in a nerve membrane [29] and produces the chaotic neurodynamics, plays a key role: it memorizes a past routing history. Using the refractory effect or the past routing history, the chaotic routing algorithm shows high performance for several types of complex network topologies such as the small-world network and the scale-free network [14-19]. Echenique et al. proposed a routing algorithm using a different approach [1,30]. In their routing algorithm [1,30], each node contains information of the shortest distance and the waiting times at adjacent nodes to determine a transmitted node of a packet. Using this information, the routing algorithm [1,30] shows high performance for the communication network. Thus, we expect that the performance of the chaotic routing algorithm [14-19] is also enhanced if the node obtains not only the shortest distance information but also the waiting-time information at adjacent nodes. Further, using memory information obtaining from the refractory effect of the chaotic neuron, the improved chaotic routing algorithm may show better performance than the Echenique routing algorithm [1,30] by introducing the waiting-time information at adjacent nodes. From the above viewpoints, we improved the previous chaotic routing algorithm [14-19] by introducing the shortest distance information and the waiting time information at adjacent nodes [20]. Then, we confirmed that the improved chaotic routing algorithm has high performance in complex networks such as small-world networks [31] and scalefree networks [32]. However, in the previous works [14- 20], we evaluated the chaotic routing algorithm for ideal communication networks, wherein each node has equal transmission capability for routing the packets and equal buffer size for storing the packets. To check whether the chaotic routing algorithm is practically applicable, it is important to evaluate its performance under realistic conditions. In 2007, M. Hu et al. proposed a realistic communication network in which the largest storage capacity and processing capability were introduced [5]. Newman et al. proposed scale-free networks with community structures [33]; these networks effectively extract communities in real complex networks using the shortest path betweenness. In addition, the scale-free networks [33] have a common structure in real complex networks such as collaboration networks or communication networks. In this study, we evaluate the chaotic routing algorithm for communication networks [5,33] to which realistic conditions are introduced. We confirmed that the chaotic routing algorithm by effectively preventing the congestion of packets, exhibits better performance than the conventional routing algorithms. Further, results indicate that the improved chaotic routing algorithm can be realized in low-cost communication networks in contrast to other conventional routing algorithms.
2. Communication Network Model
We consider an unweighted and undirected graph G = (V, E) as the communication network model, where V is a set of nodes and E is a set of links. Each node represents a host and a router in the communication network, and each link represents a physical connection between two nodes. If a packet is created at a node, the packet is stored at the tail of the buffer of the node. In addition, a packet at the head of the buffer of the node is transmitted to an adjacent node. In other words, all the packets are transmitted to their destinations according to the first-infirst-out principle. Sources and destinations of the packets are randomly selected using uniformly distributed random numbers. In addition, if a node to which a packet will be transmitted has a full buffer, the transmission of the packet is cancelled and the packet must wait for the next opportunity to be transmitted in the following step. To construct realistic communication networks, we assign the largest storage capacity and a processing capacity [5] to each node. The largest storage capacity corresponds to the maximum size of the buffer that stores the packets, and the processing capability corresponds to the maximum number of transmitting packets at a time. The largest storage capacity of the i node, Bi, is defined as
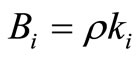 , (1)
, (1)
where ρ > 0 is a controlling parameter and ki is the degree of the i node. The largest storage capacity is proportional to the degree of the node. In other words, hub nodes in the communication network have a large memory to store packets. The processing capability of the i node, Ci, is defined as
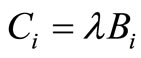 , (2)
, (2)
where Ci = λBi is a controlling parameter. If ρ and λ are set to large values, congestion of packets hardly occurs because each node has a high capacity for storing and transmitting the packets. However, the cost of such a communication network is very high. Thus, it is desirable to develop a packet routing algorithm that works well with small values of ρ and λ.
3. Realization of a Routing Algorithm with Chaotic Neurodynamics
In this section, we explain the construction of the improved chaotic routing algorithm. First, we construct a model communication network. The model communication network has N nodes, and the ith node has Ni adjacent nodes (i = 1 ··· N). Then, we assign a chaotic neural network to each node. The ith node has its own chaotic neural network, which consists of Ni neurons that correspond to Ni adjacent nodes. Firing the ijth neuron encodes the transmission of a packet from the ith node to the jth adjacent node.
In the improved chaotic routing algorithm, each node has its own chaotic neural network, which operates to minimize the distance of the transmitting packet from the ith node to its destination, and a waiting time at the jth adjacent node. To realize this routing algorithm, the internal state of the ijth neuron in the chaotic neural network is defined as follows:
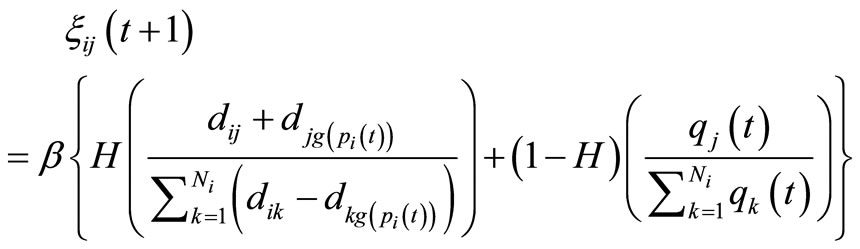 (3)
(3)
where dij is a static distance from the ith node to its jth adjacent node, pi(t) is a transmitted packet of the ith node at the tth iteration, 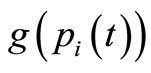 is a destination of pi(t),
is a destination of pi(t), 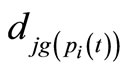 is a dynamic distance from the jth adjacent node to
is a dynamic distance from the jth adjacent node to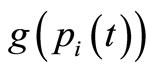 , i.e.,
, i.e., 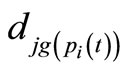 depends on
depends on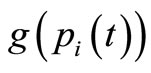 , β > 0 is a control parameter, qj(t) is the number of storing packets at the jth adjacent node at the tth iteration, and H is a quantity that determines the priority of the first term and the second term. If the jth adjacent node is the closest to
, β > 0 is a control parameter, qj(t) is the number of storing packets at the jth adjacent node at the tth iteration, and H is a quantity that determines the priority of the first term and the second term. If the jth adjacent node is the closest to 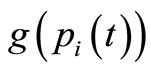 and has a small number of the stored packets, ξij(t) takes a large value. In the conventional chaotic routing algorithm [14-19], only the first term of Equation (3) is used to decide whether the jth adjacent node is an optimum one or not. The second term of Equation (3) expresses the waiting time at the jth adjacent node until pi(t) is transmitted from the jth adjacent node to the next transmitted node. By adding the waiting time, each node selects the optimum adjacent node more efficiently and flexibly.
and has a small number of the stored packets, ξij(t) takes a large value. In the conventional chaotic routing algorithm [14-19], only the first term of Equation (3) is used to decide whether the jth adjacent node is an optimum one or not. The second term of Equation (3) expresses the waiting time at the jth adjacent node until pi(t) is transmitted from the jth adjacent node to the next transmitted node. By adding the waiting time, each node selects the optimum adjacent node more efficiently and flexibly.
Next, we assigned the refractory effect [29] to each neuron. The refractory effect is one of the essential characteristics of a real neuron: after a neuron fires once, a certain period of time must pass before it can fire again. In our routing algorithm, the refractory effect plays a key role because it is used as memory information. Each node can memorize a past routing history using the refractory effect; then, an adjacent node to which many packets have been transmitted is not selected as a transmitting node of the packets for certain period. The refractory effect is described as follows:
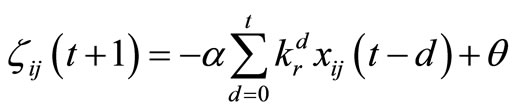 , (4)
, (4)
where α > 0 is a control parameter of the refractoriness, 0 < kr < 1 is a decay parameter of the refractoriness, xij(t) is the output of the ijth neuron at the tth iteration that will be defined in Equation (6), and θ is a threshold.
Finally, a mutual connection is assigned to each neuron. The mutual connection controls the firing rates of the neurons because frequent firing often leads to termination of packet routing. The mutual connection is defined as follows:
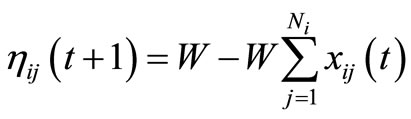 , (5)
, (5)
where W > 0 is a control parameter and Ni is the number of adjacent nodes at the ith node. Then, the output of the ijth neuron is defined as follows:
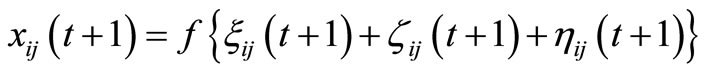 , (6)
, (6)
where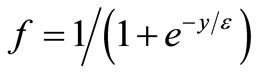 . In our routing algorithm, if xij(t+1) >
. In our routing algorithm, if xij(t+1) >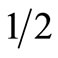 , the ijth neuron fires; a packet at the ith node is transmitted to the jth adjacent node. If the outputs of multiple neurons exceed
, the ijth neuron fires; a packet at the ith node is transmitted to the jth adjacent node. If the outputs of multiple neurons exceed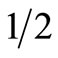 , we determine that only the neuron with the largest output fires.
, we determine that only the neuron with the largest output fires.
4. Performance Evaluation of the Routing Algorithms
To evaluate the performance of the proposed routing algorithm, we compared it with three types of conventional routing algorithms. The first one is the shortest path routing algorithm which is commonly employed by communication networks. The second one is a conventional routing algorithm with chaotic neurodynamics to which only distance information is applied [14-19]. The third one is a gain routing algorithm. The gain routing algorithm uses only Equation (3) for determining the optimum adjacent node. The difference between the routing algorithm proposed by P. Echenique et al. [1,30] and the gain routing algorithm is that Equation (3) is normalized in the case of the gain routing algorithm and the routing algorithm [1,30] uses direct information. We evaluate the routing algorithms for the scale-free networks [32] and the scale-free networks with community structures [33]. As real communication networks are scale free [34], we adopt a scale-free network topology in our study. The scale-free networks are constructed by the following procedure [32]. We begin with a complete graph with four nodes. Then, we install a new node with four links at every time step. Next, we connect four links of the newly added node to the nodes that already exist in the network with a probability 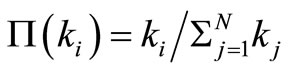 where ki is the degree of the ith node (i = 1, ···, N) and N is the number of nodes in the current iteration. In addition, the construction procedure of scale-free networks with community structure [33] follows the one described by Wu et al. [35]. We begin with O complete graphs, each of which forms a community of m nodes. In other words, the communication networks have O communities. Then, we add a new node with m links to each community at every time step. In each step, m-n links of the newly added node are connected to the nodes in the same community and n links are connected to the nodes in the other communities. The nodes in the same community and the ones in the other communities are selected by the principle of preferential attachment. Numerical simulations are conducted as follows. First, packets are created from randomly selected sources and destinations. Then, at every node, an optimal adjacent node is selected using Equations (3)-(6) and the packets are simultaneously transmitted to their destinations. We set the parameters in Equations (3)-(6) as follows: β = 5.0, H = 0.5, α = 0.8, kr = 0.82, θ = 0.5, W = 0.01, and ε = 0.05. In addition, the number of packets in the communication networks is fixed. Thus, when a packet arrives at its destination, it is removed and a new packet is created at a randomly selected source and destination. We repeat the node selection and packet transmission, I, for I = 1000. We conducted 30 simulations to average the results.
where ki is the degree of the ith node (i = 1, ···, N) and N is the number of nodes in the current iteration. In addition, the construction procedure of scale-free networks with community structure [33] follows the one described by Wu et al. [35]. We begin with O complete graphs, each of which forms a community of m nodes. In other words, the communication networks have O communities. Then, we add a new node with m links to each community at every time step. In each step, m-n links of the newly added node are connected to the nodes in the same community and n links are connected to the nodes in the other communities. The nodes in the same community and the ones in the other communities are selected by the principle of preferential attachment. Numerical simulations are conducted as follows. First, packets are created from randomly selected sources and destinations. Then, at every node, an optimal adjacent node is selected using Equations (3)-(6) and the packets are simultaneously transmitted to their destinations. We set the parameters in Equations (3)-(6) as follows: β = 5.0, H = 0.5, α = 0.8, kr = 0.82, θ = 0.5, W = 0.01, and ε = 0.05. In addition, the number of packets in the communication networks is fixed. Thus, when a packet arrives at its destination, it is removed and a new packet is created at a randomly selected source and destination. We repeat the node selection and packet transmission, I, for I = 1000. We conducted 30 simulations to average the results.
To evaluate the performance of the routing algorithms, we use the following metrics.
1)The density of the packets (D) is expressed as follows:
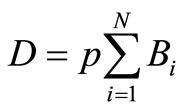 , (7)
, (7)
where Bi is the largest storage capacity defined by Equation (1) and p (0 < p < 1) is the ratio of the number of packets to the capacity of the communication network. If p increases, a large number of packets flows in the communication network.
2) The average arrival rate of the packets (A) is expressed as follows:
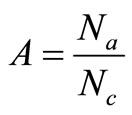 , (8)
, (8)
where Nc is the total number of packets created in the network and Na is the total number of arriving packets. The average arrival rate (A) is an important measure to evaluate the routing algorithm. By reducing or inhibiting the packet congestion in the network, the routing algorithm can maintain a higher arrival rate.
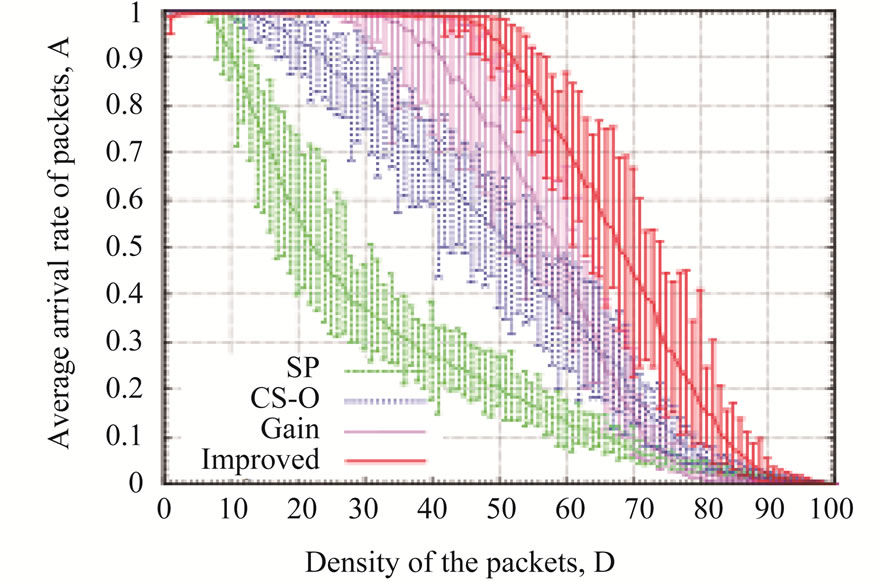
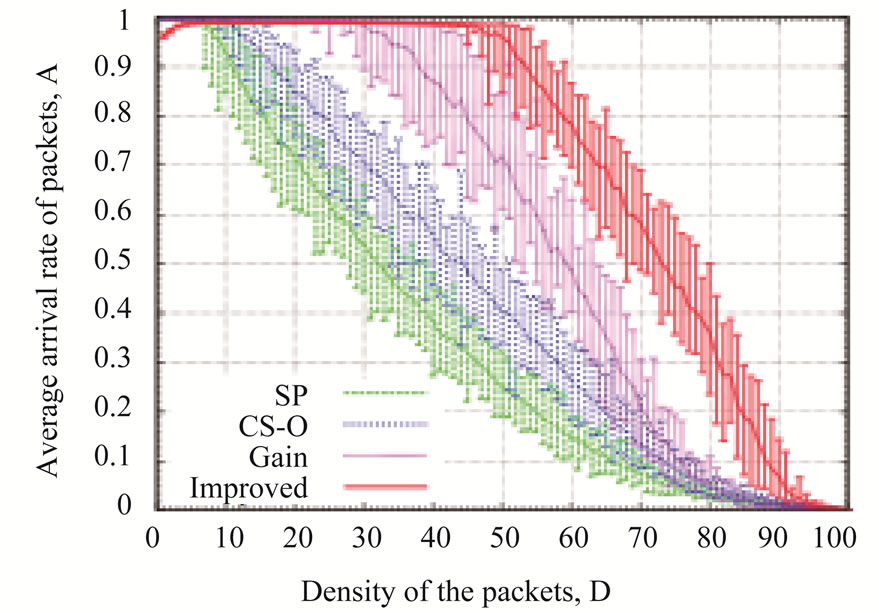
First, we evaluate the proposed routing algorithm for scale-free networks [32]. Figure 1 shows the average arrival rate of the packets by the shortest path routing algorithm (SP), the original chaotic routing algorithm (CS-O) [14-19], the gain routing algorithm (Gain), and the improved chaotic routing algorithm (Improved) for the scale-free networks. In Figure 1, the average arrival rate of the packets (A) in the improved chaotic routing algorithm (Improved) is nearly 100% if the density of the packets (D) is less than 50 in the case of λ = 0.1 (Figure 1(a)) and 60 in the cases of λ = 0.5 and λ = 1.0 (Figures 1(b) and (c)). In addition, the improved chaotic routing algorithm (Improved) has the highest arrival rate for all λ cases as compared to the other conventional routing algorithms (Figures 1(a), (b), and (c)). Furthermore, if λ increases, i.e., the nodes have a high processing capability, the performance of the improved chaotic routing algorithm (Improved) is more enhanced than the other routing algorithms. Clearly, as the congestion of the packets is alleviated in the case of the improved chaotic routing algorithm, the packets can be transmitted to the destinations using various routes, even if the density of the packets in the communication network increases.
 (a)
(a)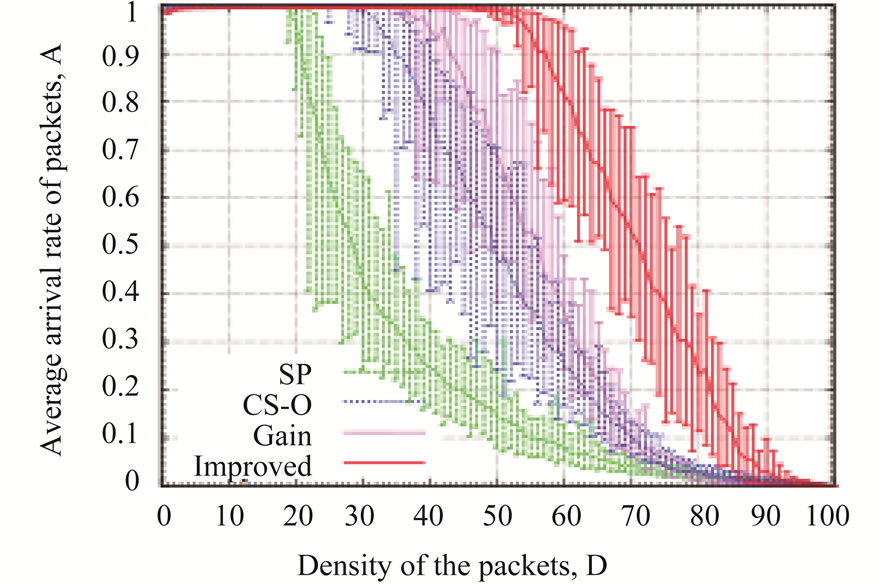 (b)
(b)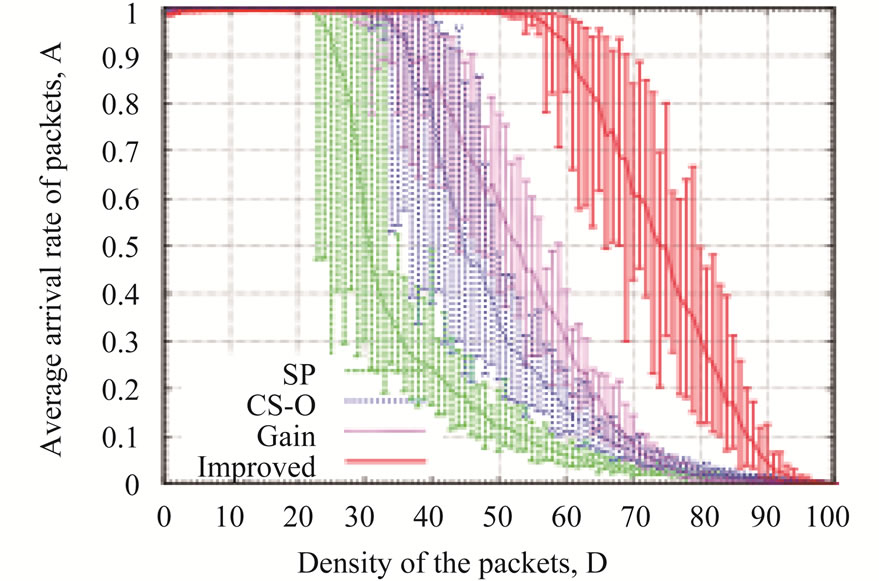 (c)
(c)
Figure 1. Relationship between the density of the packets (D) and an average arrival rate of the packets (A) for (a) λ = 0.1, (b) λ = 0.5, (c) λ = 1.0, for scale-free networks.
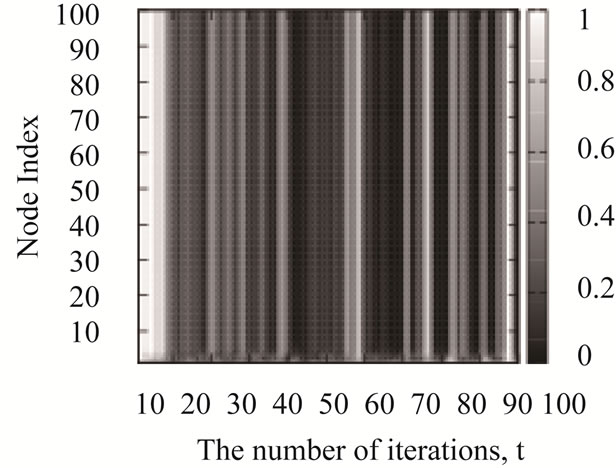
Next, we measure the congestion levels of the nodes for the scale-free networks. The congestion level of the ith node is defined by 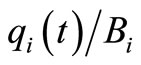 (0 <
(0 < 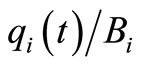 < 1). If
< 1). If 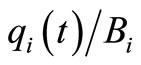 takes 1, no adjacent nodes can transmit the packets to the ith node in the tth iteration because the ith node has a full buffer. The congestion levels of the nodes by the shortest path routing algorithm (SP), the original chaotic routing algorithm (CS-O), the gain routing algorithm (Gain), and the improved chaotic routing algorithm (Improved) are shown in Figure 2. Here, we observe that several nodes are congested for all iterations by the shortest path routing algorithm (SP) and the original chaotic routing algorithm (CS-O) (Figures 2(a) and (b)). In addition, the congestion levels of the nodes show similar values if the number of iterations is greater than 80 in the case of the gain routing algorithm (Gain); this is in contrast to the shortest path routing algorithm (SP) and the original chaotic routing algorithm (CS-O) (Figure 2(c)). Further, in Figures 2(a), (b), and (c), we can observe that the congestion levels have two separate states: non congested states (white) and congested states (black). Moreover, once the state of the node changes, it remains unchanged throughout the simulation. This phenomenon is known as impermeability of the network, which was originally studied by Echenique et al. [30]. On the other hand, in the case of the improved chaotic routing algorithm (Improved), almost all the nodes are non-congested. Then, by the improved chaotic routing algorithm, the packets are reliably transmitted to their destinations.
takes 1, no adjacent nodes can transmit the packets to the ith node in the tth iteration because the ith node has a full buffer. The congestion levels of the nodes by the shortest path routing algorithm (SP), the original chaotic routing algorithm (CS-O), the gain routing algorithm (Gain), and the improved chaotic routing algorithm (Improved) are shown in Figure 2. Here, we observe that several nodes are congested for all iterations by the shortest path routing algorithm (SP) and the original chaotic routing algorithm (CS-O) (Figures 2(a) and (b)). In addition, the congestion levels of the nodes show similar values if the number of iterations is greater than 80 in the case of the gain routing algorithm (Gain); this is in contrast to the shortest path routing algorithm (SP) and the original chaotic routing algorithm (CS-O) (Figure 2(c)). Further, in Figures 2(a), (b), and (c), we can observe that the congestion levels have two separate states: non congested states (white) and congested states (black). Moreover, once the state of the node changes, it remains unchanged throughout the simulation. This phenomenon is known as impermeability of the network, which was originally studied by Echenique et al. [30]. On the other hand, in the case of the improved chaotic routing algorithm (Improved), almost all the nodes are non-congested. Then, by the improved chaotic routing algorithm, the packets are reliably transmitted to their destinations.
Next, we evaluated the routing algorithms for the scale-free networks with community structures [32]. Figure 3 shows the average arrival rate of the packets for the shortest path routing algorithm (SP), the original chaotic routing algorithm (CS-O), the gain routing algorithm (Gain), and the improved chaotic routing algorithm (Improved) for the scale-free networks with community structures. In these simulations, we set ρ in Equation (1) to 5.0 and λ in Equation (2) to 0.2. In Figure 3, the improved chaotic routing algorithm (Improved) has a higher average arrival rates of the packets (A) for all O cases than the other conventional routing algorithms (Figures 3(a), (b), and (c)). In addition, the performance of the improved chaotic routing algorithm (Improved) is enhanced if the number of communities increases. Then, the improved chaotic routing algorithm (Improved) has the highest arrival rate among the other routing algorithms (Figures 3(a), (b), and (c)).
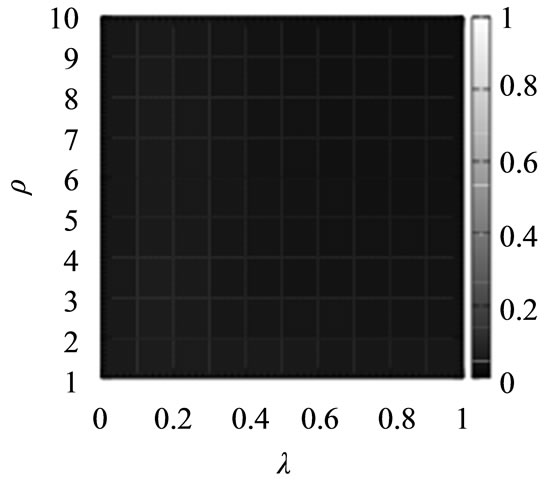
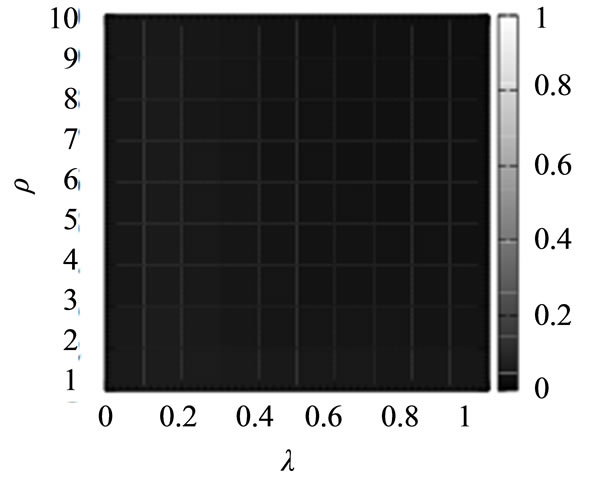
Further, it is essential to evaluate the routing algorithms for the communication networks with wide a range of values of ρ and λ in Equations (1) and (2). Figure 4 shows the average arrival rate of the packets for the shortest path routing algorithm (SP), the original chaotic routing algorithm (CS-O), the gain routing algorithm (Gain), and the improved chaotic routing algorithm (Improved) for the scale-free networks with a wide range of values of ρ and λ. From Figures 4(a) and (b), the shortest path routing algorithm (SP) and the original chaotic routing algorithm (CS-O) show a lower arrival rate of the packets than the gain routing algorithm (Gain) and the improved chaotic routing algorithm (Improved), even if ρ and λ increase. In addition, if λ increases, the gain routing algorithm (Gain) shows a higher arrival rate of the packets.
 (a)
(a)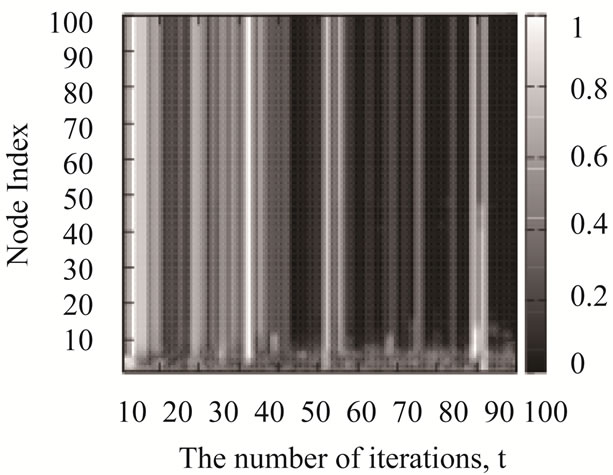 (b)
(b)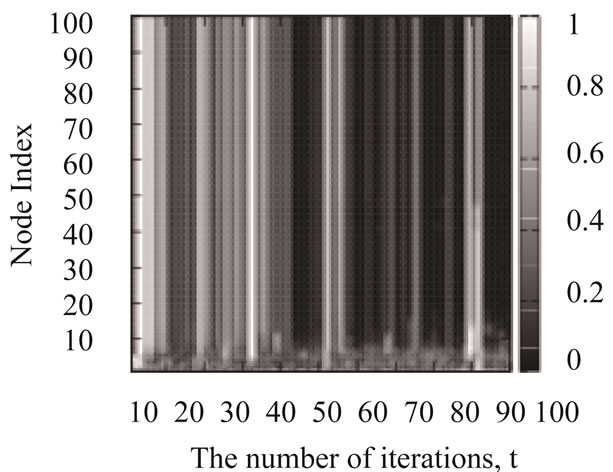 (c)
(c)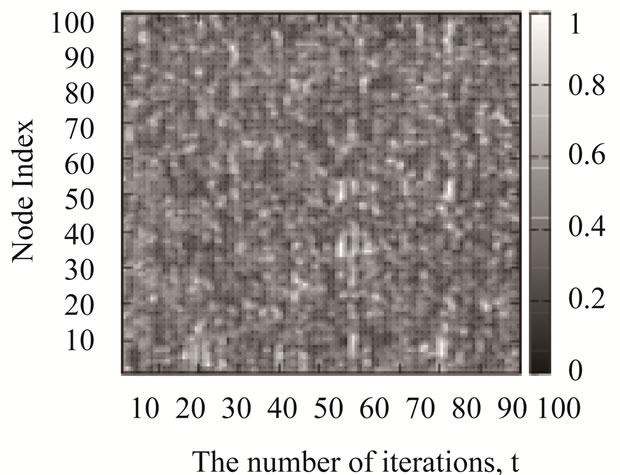 (d)
(d)
Figure 2. Congestion levels of the nodes by (a) the shortest path routing algorithm (SP) (b) the chaotic routing algorithm (CS-O) [14-19], (c) the gain routing algorithm (Gain), and (d) the improved chaotic routing algorithm (Improved) for the scale-free networks. We set control parameters ρ and λ in Equations (1) and (2) to 5.0 and 1.0, and the density of the packets (D) to 40 in these numerical simulations.
 (a)
(a)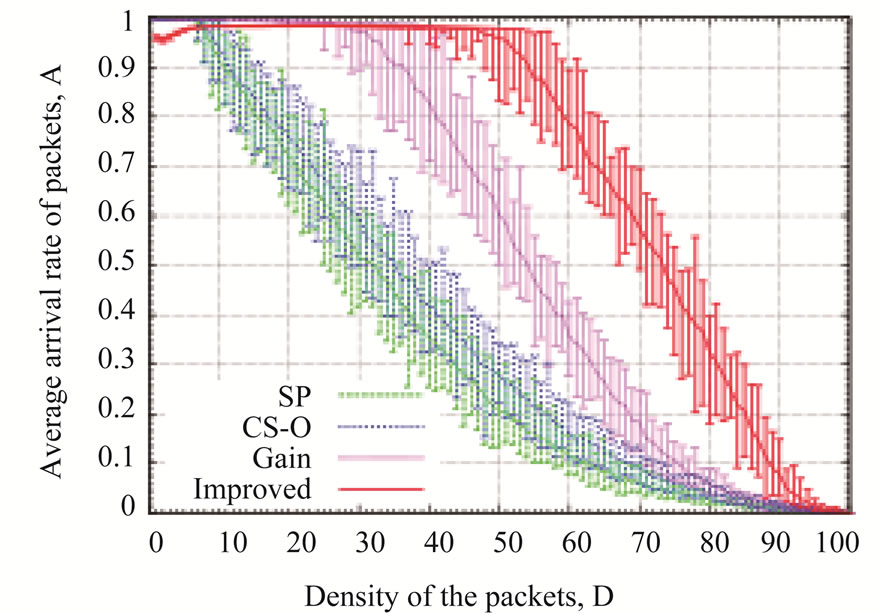 (b)
(b)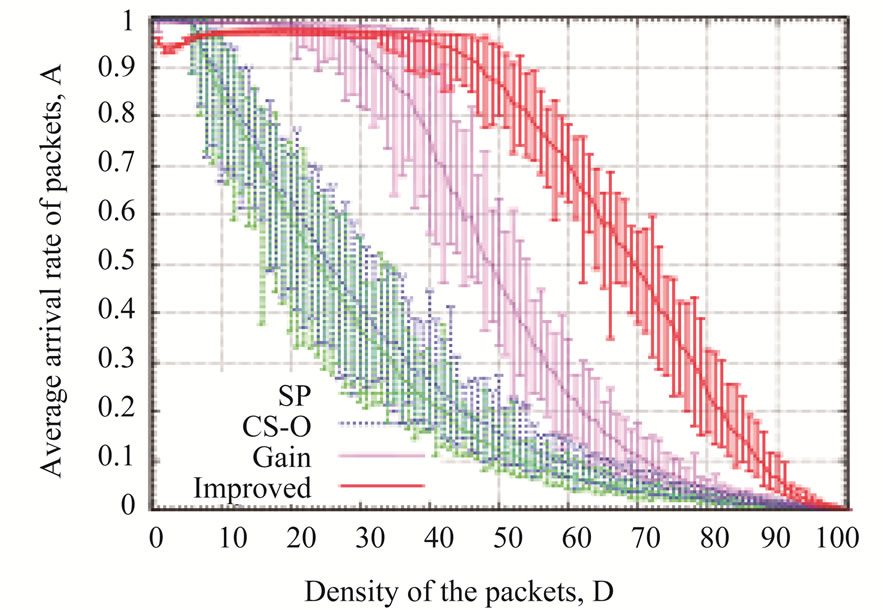 (c)
(c)
Figure 3. Relationship between the density of the packets (D) and the average arrival rate of the packets (A) for (a) the number of communities O = 5, (b) O = 10, and (c) O = 15.
The average arrival rates for the shortest path routing algorithm (SP), the original chaotic routing algorithm (CS-O), the gain routing algorithm (Gain), and the improved chaotic routing algorithm (Improved) for the scale-free networks with community structures [33] obtained by varying ρ and λ are shown in Figure 5. Here,
 (a)
(a)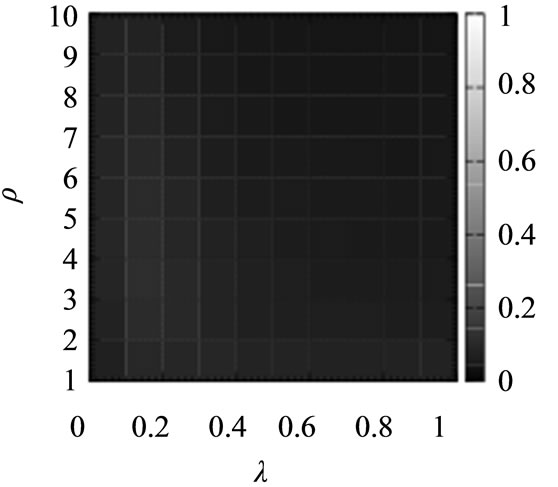 (b)
(b)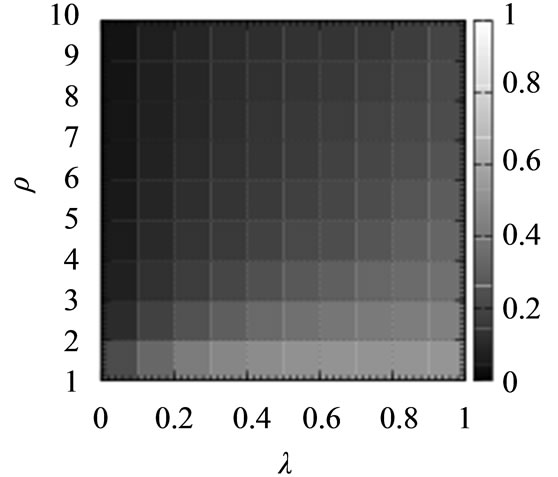 (c)
(c)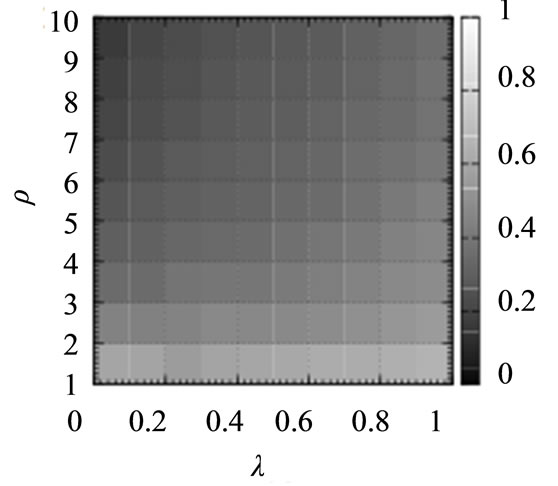 (d)
(d)
Figure 4. Average arrival rate of the packets for the shortest path routing algorithm (SP), the chaotic routing algorithm (CS-O) [14]-[19], the gain routing algorithm (Gain), and the improved chaotic routing algorithm (Improved) for the scale-free networks with a wide range of values of ρ and λ. In these numerical simulations, we set the density of the packets (D) to 75.
 (a)
(a)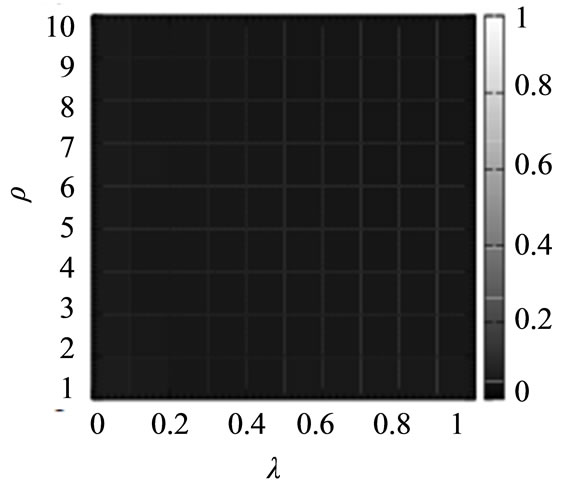 (b)
(b)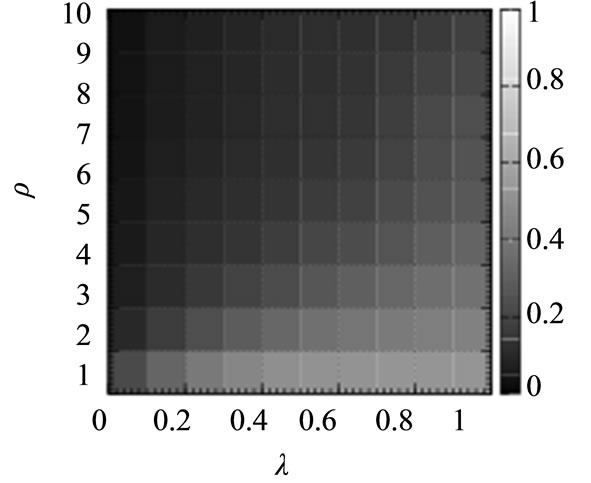 (c)
(c)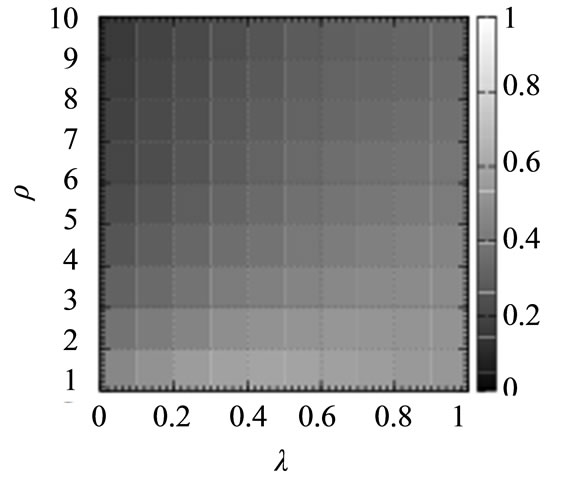 (d)
(d)
Figure 5. Average arrival rate of the packets for the shortest path routing algorithm (SP), the chaotic routing algorithm (CS-O) [14-19], the gain routing algorithm (Gain), and the improved chaotic routing algorithm (Improved) for the scale-free networks with community structures for a wide range of values of ρ and λ. In these numerical simulations, we set the density of the packets (D) to 75.
the results show the same tendency as compared to those for the scale-free networks (Figure 4), and we observe that the improved chaotic routing algorithm (Improved) transmits more packets to the destinations for various values of ρ and λ than the gain routing algorithm for the scale-free networks with community structures (Figures 5(c) and (d)).
From Figures 4 and 5, the gain routing algorithm can transmit the packets to their destination if the nodes in the communication networks have a high processing capability. However, the construction of such a network is expensive, and it is difficult to apply the gain routing algorithm as a routing method to real communication networks. On the other hand, the improved chaotic routing algorithm has high performance for both poor and rich settings of the communication networks. These results indicate that the improved chaotic routing algorithm has much possibility as the routing method for transmitting the packets in the real communication networks because the improved chaotic routing algorithm can be realized on the low-cost communication networks. In addition, the chaotic routing algorithm shows higher performance than the other routing algorithms in both scale-free networks and scale-free networks with community structures. These results indicate that the chaotic routing algorithm is applicable to any scale-free complex network.
5. Conclusions
In this paper, to inspect the applicability of the routing algorithm employing chaotic neural networks, we evaluated the chaotic routing algorithm for the communication networks to which realistic conditions were introduced. First, to improve the routing algorithm employing chaotic neural networks, we introduced information on the waiting time to transmit a packet at adjacent nodes into chaotic neurons. Then, we examined the routing algorithms for the scale-free networks and showed that the improved chaotic routing algorithm has the highest arrival rate of packets, even if the density of the packets increases. Further, the improved chaotic routing algorithm exhibits lower congestion levels by effectively avoiding the impermeability of the communication networks using the refractory effect. In addition, the results of the numerical simulations indicate that the improved chaotic routing algorithm has higher performance for the lowcost communication networks. Further, the obtained results indicate that the improved chaotic routing algorithm can possibly be applied to real communication networks. In our future work, the use of memory effect may be combined with the use of cellular automata for congestion elimination. While evaluating the performance of routing algorithms, an order parameter may be used to indicate the phase transition point between free state and congested state for the network under study [1,7-9,30]. A novel evaluation method may be proposed for routing algorithms using the order parameter.
The research of T.K. was partially supported by a Grant-in-Aid for Young Scientists (B) from JSPS (No. 23700180).
REFERENCES
- P. Echenique, J. Gómez-Gardenes and Y. Moreno, “Improved Routing Strategies for Internet Traffic Delivery,” Physical Review E, Vol. 70, No. 5, 2004, Article ID: 056105. doi:10.1103/PhysRevE.70.056105
- T. Ohira and R. Sawatari, “Phase Transition in a Computer Network Traffic Model,” Physical Review E, Vol. 58, 1998, pp. 193-195. doi:10.1103/PhysRevE.58.193
- A. Arenas, A. Díaz-Guilera and R. Guimerà, “Communication in Networks with Hierarchical Branching,” Physical Review Letters, Vol. 86, 2002, pp. 3196-3199. doi:10.1103/PhysRevLett.86.3196
- L. Zhao, Y.-C. Lai, K. Park and N. Ye, “Onset of Traffic Congestion in Complex Network,” Physical Review E, Vol. 71, No. 2, 2005, Article ID: 026125. doi:10.1103/PhysRevE.71.026125
- M.-B. Hu, W.-X. Wang, R. Jiang, Q.-S. Wu and Y.-H. Wu, “Phase Transition and Hysteresis in Scale-Free Network Traffic,” Physical Review E, Vol. 75, No. 3, 2007, Article ID: 036102. doi:10.1103/PhysRevE.75.036102
- W.-X. Wang, B.-H. Wang, C.-Y. Yin, Y.-B. Xie and T. Zhou, “Traffic Dynamics Based on Local Routing Protocol on a Scale-free Network,” Physical Review E, Vol. 73, No. 2, 2006, Article ID: 026111. doi:10.1103/PhysRevE.73.026111
- G. Yan, T. Zhou, B. Hu, Z.-Q. Fu and P. M. Hui, “Efficient Routing on Complex Networks,” Physical Review E, Vol. 73, No. 4, 2006, Article ID: 046108. doi:10.1103/PhysRevE.73.046108
- H. Zhang, Z. Liu, M. Tang and P. M. Hui, “An Adaptive Routing Strategy for Packet Delivery in Complex Networks,” Physics Letters A, Vol. 364, No. 3-4, 2007, pp. 177-182. doi:10.1016/j.physleta.2006.12.009
- D. Wang, Y. Jing and S. Zhang, “Traffic Dynamics Based on A Traffic Awareness Routing Strategy on Scale-free Networks,” Physica A, Vol. 387, No. 12, 2008, pp. 3001- 3007. doi:10.1016/j.physa.2008.01.085
- T. Horiguchi and S. Ishioka, “Routing Control of Packet Flow Using a Neural Network,” Physica A, Vol. 297, No. 3-4, 2001, pp. 521-531. doi:10.1016/S0378-4371(01)00229-1
- T. Horiguchi, K. Hayashi and A. Tretiakov, “Reinforcement Learning for Congestion-Avoidance in Packet Flow, Physica A, Vol. 349, No. 1-2, 2005, pp. 329-348. doi:10.1016/j.physa.2004.10.015
- T. Kimura, H. Nakajima and T. Ikeguchi, “A Packet Routing Method for Complex Networks by a Stochastic Neural Network,” Physica A, Vol. 376, 2007, pp. 658-672. doi:10.1016/j.physa.2006.10.061
- T. Kimura. T. Ikeguchi and Chi. K. Tse, “Efficient Routing Strategy with Memory Information for Complex Networks,” American Journal of Operations Research, Vol. 2, No. 1, 2012, pp. 73-81. doi:10.4236/ajor.2012.21008
- T. Kimura and T. Ikeguchi, “A Packet Routing Method using Chaotic Neurodynamics for Complex Networks,” Lecture Notes in Computer Science, Vol. 4132, 2006, pp. 1012-1021. doi:10.1007/11840930_105
- T. Kimura and T. Ikeguchi, “Chaotic Dynamics for Avoiding Congestion in the Computer Networks,” Lecture Notes in Computer Science, Vol. 4224, 2006, pp. 363-370. doi:10.1007/11875581_44
- T. Kimura and T. Ikeguchi, “Optimization for Packet Routing Using a Chaotic Neurodynamics,” Proceeding of IEEE International Symposium on Circuits and Systems, 2006, pp. 2257-2260.
- T. Kimura and T. Ikeguchi, “A New Algorithm for Packet Routing Problems using Chaotic Neurodynamics and Its Surrogate Analysis,” Neural Computation and Applications, Vol. 16, No. 6, 2007, pp. 519-526. doi:10.1007/s00521-007-0099-5
- T. Kimura and T. Ikeguchi, “An Efficient Routing Strategy with Load-Balancing for Complex Networks,” Proceedings of International Symposium on Nonlinear Theory and Its Applications, 2007, pp. 31-34
- T. Kimura and T. Ikeguchi, “An Optimum Strategy for Dynamic and Stochastic Packet Routing Problems by Chaotic Neurodynamics,” Integrated Computer-Aided Engineering, Vol. 14, 2007, pp. 307-322.
- T. Kimura and T. Ikeguchi, “Communication in the Computer Networks with Chaotic Neurodynamics,” In: Complexity, Applications of Nonlinear Dynamics, Springer, Berlin, 2009, pp. 417-420.
- M. Hasegawa, T. Ikeguchi and K. Aihara, “Combination of Chaotic Neurodynamics with the 2-Opt Algorithm to Solve Traveling Salesman Problems,” Physical Review Letters, Vol. 79, 1997, pp. 2344-2347. doi:10.1103/PhysRevLett.79.2344
- M. Hasegawa, T. Ikeguchi and K. Aihara, “Solving Large Scale Traveling Salesman Problems by Chaotic Neurodynamics,” Neural Networks, Vol. 15, No. 2, 2002, pp. 271-283. doi:10.1016/S0893-6080(02)00017-5
- M. Hasegawa, T. Ikeguchi, and K. Aihara, “Exponential and Chaotic Neurodynamical Tabu Searches for Quadratic Assignment Problems,” Control and Cybernetics, Vol. 29, 2000, pp. 773-788.
- M. Hasegawa, T. Ikeguchi, K. Aihara and K. Itoh, “A Novel Chaotic Search for Quadratic Assignment Problems,” European Journal of Operational Research, Vol. 139, No. 3, 2002, pp. 543-556. doi:10.1016/S0377-2217(01)00189-8
- T. Matsuura and T. Ikeguchi, “Refractory Effects of Chaotic Neurodynamics for Finding Motifs from DNA Sequences,” Lecture Notes in Computer Science, Vol. 4224, 2006, pp. 1103-1110. doi:10.1007/11875581_131
- T. Matsuura and T. Ikeguchi, “Chaotic Search for Traveling Salesman Problems by Using 2-opt and Or-opt Algorithms,” Lecture Notes in Computer Science, Vol. 5164, 2008, pp. 587-596. doi:10.1007/978-3-540-87559-8_61
- T. Hoshino, T. Kimura and T. Ikeguchi, “A Metaheuristic Algorithm for Solving Vehicle Rouging Problems with Soft Time Windows by Chaotic Neurodynamics,” Transactions of IEICE, Vol. J90-A, 2007, pp. 431-441.
- T. Hoshino, T. Kimura and T. Ikeguchi, “A New Diversification Method to Solve Vehicle Routing Problems using Chaotic Dynamics,” Complexity, Applications of Nonlinear Dynamics, Springer, 2009, pp. 409-412.
- K. Aihara, T. Tanabe and M. Toyoda, “Chaotic Neural Network,” Physics Letters A, Vol. 144, No. 6-7, 1990, pp. 333-340. doi:10.1016/0375-9601(90)90136-C
- P. Echenique, J. Gómez-Gardenes and Y. Moreno, “Dynamics of Jamming Transitions in Complex Networks,” Europhysics Letters, Vol. 71, No. 2, 2005, pp. 325-331. doi:10.1209/epl/i2005-10080-8
- D. J. Watts and S. H. Strogatz, “Collective Dynamics of Small-World Networks,” Nature, Vol. 393, 1998, pp. 440-442. doi:10.1038/30918
- A.-L. Barabási and R. Albert, “Emergence of Scaling in Random Networks,” Science, Vol. 286, No. 5439, 1999, pp. 509-512. doi:10.1126/science.286.5439.509
- M. E. J. Newman and M. Girvan, “Finding and Evaluating Community Structure in Networks,” Physical Review E, Vol. 69, No. 2, 2004, Article ID: 026113. doi:10.1103/PhysRevE.69.026113
- M. Faloutsos, F. Faloutsos and C. Faloutsos, “On PowerLaw Relationships of the Internet Topology,” ACM SIGCOMM Computer Communication Review, Vol. 29, 1999, pp. 251-262. doi:10.1145/316194.316229
- J.-J. Wu, Z.-Y. Gao and H.-J. Sun, “Cascade and Breakdown in Scale-Free Networks with Community Structure,” Physical Review E, Vol. 74, No. 6, 2006, Article ID: 066111. doi:10.1103/PhysRevE.74.066111

