ABSTRACT

In this paper, the definition of weak dominance is proposed for a NTU game and two new solution concepts of NTU games are introduced: the refined core and weakly stable set. The relationship is explored among the core, the weakly stable set and the refined core.

1. Introduction

Various solutions [1-5] expressing some concern for fairness have been proposed for cooperative games in coalitional form with non-transferable utility (NTU). The main ones are the Harsanyi solution [6], the Shapley NTU solution [7], the symmetric egalitarian solution [8], and the consistent solution [9]. Hart [10] compared the Harsanyi solution, the Shapley NTU solution, and the consistent solution in a simple example.

For games with transferable utility, a strategy is weakly dominated if there exists another strategy of the same player that is never worse and sometimes strictly better with respect to what the other players do. Extant solutions translate TU solution concepts to the NTU case by utilizing endogenously determined utility weight vectors, which can violate notions of equity. Lejano [11] develops a new solution procedure that tries to resolve this longstanding problem. However, there still remains a need for new NTU solution concepts.

The purpose of this paper is to provide two new solution concepts for a NTU game: the refined core and weakly stable set. We begin with introducing the definition of weak dominance in NTU games. After that, we show that the payoffs in core are refined by a subset 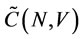and give the definition of a weakly stable set and explore the relation among the core, the weakly stable set, and the refined core.

2. Some Concepts for a NTU Game

Let be a finite set of players. A coalition is a non-empty subset of N. For every 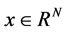the restriction of x to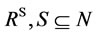, is denoted by.

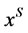A cooperative game with non-transferable utility is a pair (N, V), where N is the set of players and V is a mapping which for each coalition S, defines a characteristic set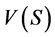, satisfying:

1) is a non-empty, closed subset of.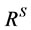

2) 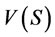is comprehensive, i.e. if 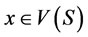and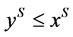, then. Here

.

3) The set is compact, for all.

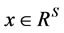The characteristic set 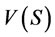can be interpreted as the set of outcomes the players in S which can guarantee themselves without cooperating with the player in.

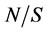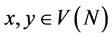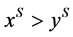Given (N, V), let. We say x dominates y through S (notation: or) if there exists an coalition, such that and i.e.,.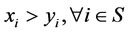

The core of NTU games is defined by the set of all undominated payoffs. We denote it by, therefore,

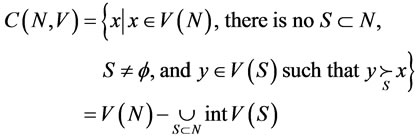
3. Weak Dominance and the Refined Core

Given a game with no-transferable utility (N, V), let be a feasible payoff for a player. For the NTU game we study, assume that the scale of players’ utility is not always the same and no side payments are allowed. Therefore, the payoffs of players that belong to a coalition S should not be summed up.

Shapley (1969) introduced a vector which can make the scale of players’ utility unanimous. So the utilities of all players are comparable. But his research did not consider the sum of some players’ utility that belongs to a coalition.

Let K denote the class of NTU-games, and let denote a subclass of NTU-games that all players have the same utility scale. Players in subclass 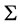can’t transfer their utility, but they can research and contrast the sum of some players’ utility.

We introduce the definition of weak dominance and draw some conclusions in the subclass 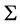of NTU games by comparing the sum utility of players that belongs to a same coalition.

Definition 1. Given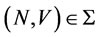,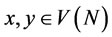. y is weakly dominated by x through coalition S (notation:

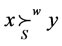or) if there exists 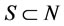such that 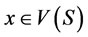and.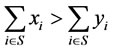

We use condition 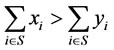instead of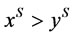

in the definition of dominance. It is a weaker condition.

If, then. But the converse is not true.

And weak dominance is not possible through the whole players’ coalition and single player’s coalitions, which is the same as the definition of dominance.

Denote the set of all payoffs that are not weakly dominated by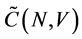. Hence,

Theorem 1. Given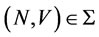, there exists a payoff that weakly dominates if and only if there exists a coalition, such that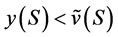, where

,.

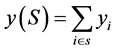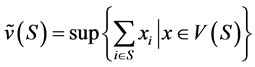Proof: For every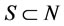, there always exists 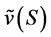because 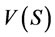is a characteristic set satisfying conditions 1 - 3 in the definition of a NTU game.

For the part “only if”, we suppose that there exist a coalition and a payoff, such that

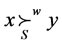, thus.

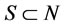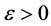For the part “if”, there exists a coalition, such that. Hence, there exists, such that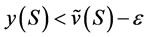. Because 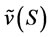is the supremum of set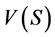, there exists a payoff, such that

. That is,.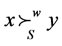

Theorem 2. Given, 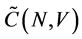is a subset of the core.

Proof: For any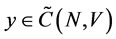, there is no 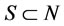and

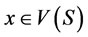, such that.

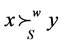If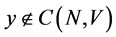, there exist 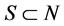and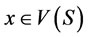, such that. That is, if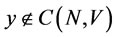, there exist

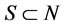and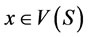, such that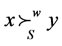. Thereforefor all, we have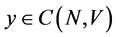. Hence,.

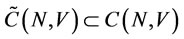Here 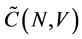is a new solution of the NTU game. We use the definition of weak dominance to refine the payoffs in core of the NTU game. Then we get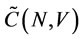. So it is a refined solution of the NTU game.

Theorem 3. Given,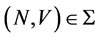

.

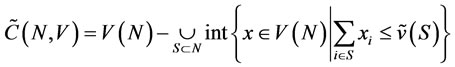Proof: Denote

.

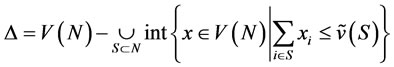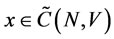For. For every, ifthere exists, such that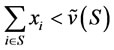. By Theorem 1, there exists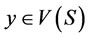, such that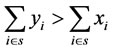which is contradictory to.

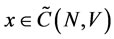For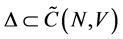. Conversely, for every, if, there exists a coalition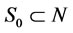, by Theorem 1, such that. Then we have

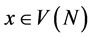, and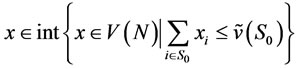. But this means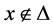. The contradiction proves. So.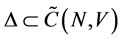

Therefore, .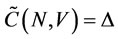

4. Weakly Stable Set of NTU Game

In NTU games, a stable set is a subset of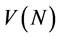, satisfying:

No payoff in this subset dominates another. (Internal stability);

Any payoff outside this subset is dominated by some payoff in it. (External stability);

We develop the definition of weak stable sets by the definition of weak dominance of a NTU game and explore the relation among the core and the weakly stable set.

Definition 1. Given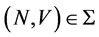, a weak stable set is a subset of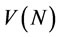, satisfying:

No payoff in this subset weakly dominates another. (Internal stability);

Any payoff outside this subset is weakly dominated by some payoff in it. (External stability).

If the core is a stable set, it is the unique stable in cooperative games. Gao (1998) proved that the conclusion applies to weakly stable sets of a cooperative game. We show that this applies to weakly stable sets of a NTU game by Theorem 4.

Theorem 4. If the core is a weakly stable set of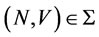, it is the unique weak stable set.

Proof: Suppose the core is a weakly stable set, and Z is another weakly stable set.

Each payoff is weakly dominated by some payoff in Z. But the core 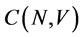is a set of undominated payoff. Therefore,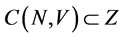. We have.

Conversely, assume, there exists

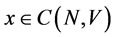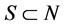and, such that. This fails to satisfy with the internal stability of Z because .

5. Acknowledgements

This work is supported by the National Natural Science Foundation of China (No.71003057, 70871064); Natural Science Foundation of Shandong Province (No.ZR2010 GQ001), China.

REFERENCES