International Journal of Organic Chemistry
Vol.08 No.01(2018), Article ID:82939,18 pages
10.4236/ijoc.2018.81010
Pseudo Jahn-Teller Effect in Puckering and Planarization of Heterocyclic Compounds
Natalia Gorinchoy
Institute of Chemistry, Academy of Sciences of Moldova, Kishinev, Republic of Moldova
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 4, 2017; Accepted: March 9, 2018; Published: March 12, 2018
ABSTRACT
The goal of this brief partly review paper is to summarize the results of the works published over the last few years regarding the origin of the out-of-plane distortions (puckering) of heterocyclic compounds. In all the papers devoted to this problem, it is shown that the instability of planar configurations of heterocyclic molecules leading to symmetry breaking and distortions is induced by the pseudo Jahn-Teller effect (PJTE). Special attention in this work is paid to the mechanism of suppression and enhancement of the PJTE distortions of heterocycles by oxidation, reduction, and chemical substitutions. It is demonstrated that oxidation of 1,4-dithiine containing compounds leads to suppression of the PJTE and to restoration of their planar nuclear configurations. An example of a dibenzo[1,2]dithiine molecule is used to demonstrate the mechanism of enhancement of the PJTE by reduction. It is shown that the reduction of the neutral C12H8S2 molecule up to the dianion (C12H8S2)2− enhances the PJTE, followed by the S-S bond cleavage and significant structural distortions of the system. The change of the PJTE by chemical substitutions, accompanied either by puckering or by planarization of heterocyclic compounds, is discussed using as examples 1,4-ditinine and its S-oxygenated derivatives.
Keywords:
Pseudo Jahn-Teller Effect (PJTE), Vibronic Coupling, Puckering and Planarization in Heterocyclic Systems

1. Introduction
From general space-symmetry considerations, one would expect that in an isotropic environment any molecular system should have the highest possible symmetry, but in fact we see that in many cases the symmetry of the system is much lower (see [1] ). In this respect, cyclic molecules (including the heterocyclic ones) should be at least planar, and any deviation from the planar structure (puckering) can be described through the instability of the reference planar high-symmetry nuclear configuration. A general approach to handle instabilities and structural changes in molecular systems in non-degenerate states is the pseudo Jahn-Teller effect (PJTE). It was proved that the PJTE is the only source of instability of high-symmetry configurations of molecules or solid in non-degenerate states (See, e.g., the monographs [2] [3] , and the reviews [1] [4] [5] and references therein). The phenomenon of puckering as due to the PJTE was first formulated in [3] , and then employed to explain the origin of the out-of-plane distortions of a variety of cyclic and heterocyclic systems [6] - [11] . Knowledge of the mechanism of puckering of cyclic molecules provides the key to understanding how one can influence the system to suppress this effect and to flatten the system. In a recent review of Bersuker [12] devoted to manipulation of structure of two-dimensional (2D) or quasi 2D systems, the methods of targeted external influence that suppresses the PJTE are demonstrated on a series of molecular and extended 2D systems including silicene, phosphorene, germanene, graphitic carbon nitride, etc.
In this paper, we first summarize the results of studies published over the last few years regarding the PJTE origin of the puckered structures of heterocyclic compounds. Then, the possibility of enhancement and suppression of the pseudo Jahn-Teller effect by oxidation, reduction and chemical substitutions and therefore the possibility of changing the structure of the systems is discussed in more detail using a series of heterocyclic compounds as examples.
Chart 1 lists the heterocyclic systems which were studied recently with regard to the PJTE in the origin of their puckering. The figures in the first column of Chart 1 show schematically the initial planar and equilibrium configurations of the compounds under study, with the indication of the symmetry of the configurations and the type of distortions. The second column indicates the PJTE problem, which was solved in the corresponding work.
The first group of compounds includes 1,4-dithiine molecules C4S2L4 [10] with a variety of the ligands (L = H, F, Cl, Br), S-oxygenated derivatives of 1,4-dithiine, two tricyclic systems (thianthrene [11] and C6S8 with two S-atoms in the 1,4-position of the central six-membered ring [13] ), and 1,4-dihydropyrazine and its derivatives C4N2H4L2 [15] in which two imide hydrogen atoms are replaced with halogens (L = F, Cl, Br). All these compounds are unstable in the high-symmetry planar nuclear configuration of D2h symmetry, in the equilibrium configuration of C2v symmetry they are bent at the S-S axis. The exception is the tricyclic C6S8 molecule, which has C2h symmetry in the planar configuration and C2 symmetry in the equilibrium.
The next group of molecules includes 1,2-dichalcogenins, 1,2-C4X2L4, with X = O, S, Se, Te and L = H, F [10] , two tricyclic species C6S8 and containing two S-atoms in the 1,2-positions of the central six-membered ring and one

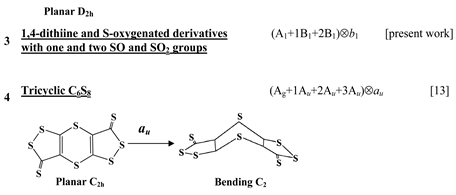

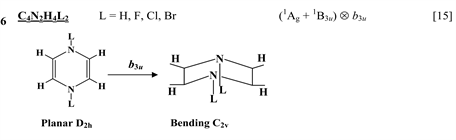
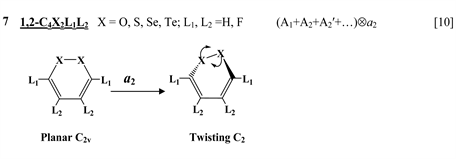
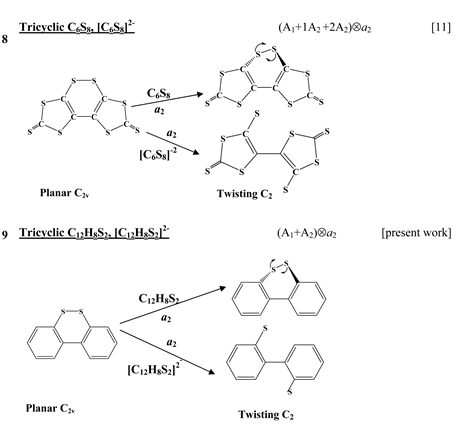

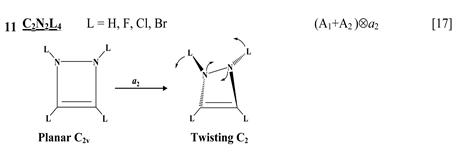
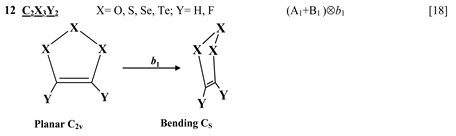
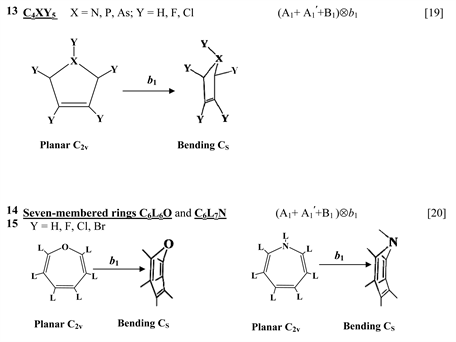
Chart 1. List of heterocyclic systems studied with respect to the PJTE origin of their puckering.
thione (C=S) bond in the five-membered rings on its either side [11] , two tricyclic molecules C12H8S2 and (C12H8S2)2− [this work], 3,6-pyridazinedione derivatives N2C4H2Y2Z2 (Y = O, S, Se; Z = H, F, Cl, Br) [16] , and 1,2-diazetes C2N2L4 with L = H, F, Cl, Br [17] . The planar configuration of these systems is unstable with respect to the twisting coordinate of a2 symmetry that leads to a puckered equilibrium structure of C2 symmetry.
Finally, one can distinguish the third group of five-membered heterocyclic molecules of the type C2X3Y2 (X = O, S, Se, Te; Y = H, F) [18] and C4XY5 (X = N, P, As; Y = H, F, Cl) [19] , and the seven-membered rings C6Y6O and C6Y7N with Y = H, F, Cl, Br [20] . As in the previous cases, in these compounds the planar nuclear configuration of C2v symmetry is distorted along the out-of-plane b1 coordinate of instability that leads to equilibrium puckered structure of Cs symmetry.
In the next Section 2, we give the basic formulas of the PJTE theory, which will be needed in discussing the results. In Section 3, the possibility of flattening the 1,4-dithiine containing compounds by suppressing the PJTE via oxidation is discussed. The enhancement of the PJTE induced distortion by reduction is analyzed in Section 4 using the dibenzo[1,2]dithiine molecule as an example. In the last Section 5, the change of the PJTE by chemical substitution, accompanied by a change in the structure of heterocyclic compounds, is discussed using, as examples, 1,4-ditinine and its S-oxygenated derivatives. Geometry optimization and vibration frequency analysis for all the molecules considered in Sections 4 and 5 were performed at the B3LYP level of the DFT method [21] . The Pople’s 6-31+G(d,p) split basis sets [22] were utilized in all steps of the calculations. The potential energy profiles along the distortion coordinates were calculated with the CISD method. The applied active space for the C12H8S2 and (C12H8S2)2− species was composed of eight electrons and nine active orbitals, while that for the 1,4-ditinine S-oxygenated derivatives included ten electrons and ten active states. All the calculations were carried out using the GAUSSIAN 09 program package [23] .The numerical values of the vibronic coupling constants were estimated by means of fitting the solutions of the secular equations to the ab initio calculated energy profiles.
2. Basic Formulas of the PJTE Theory
The theory of the PJTE is well developed (see, for example, [1] [2] [3] [4] ). In this approach the problem of the stability or instability of molecular nuclear configuration is reduced to estimation of the curvature K of the adiabatic potential energy surface (APES) in direction of any normal displacement Q, at the high-symmetry configuration Q0 for which the first derivatives are zero. At the minimum of the APES , while K < 0 if the high-symmetry configuration is unstable.
The exact expression for K of any molecular system in nondegenerate ground state Ψ0 can be obtained in the second order perturbation theory with respect to small nuclear displacements Q:
(1)
The first term in Equation (1), K0, is the so-called primary force constant. It determines the restoring force arising when the nuclei are displaced with respect to the “frozen” electron distribution. The second term, Kv,
(2)
is the vibronic contribution to the curvature coming from the vibronic interaction of the ground Ψ0 and excited Ψi states under the nuclear displacements, E0 and Ei are their energies. For the ground state this term is always negative. The matrix elements F0i in Equations (1) and (2),
(3)
are the off-diagonal vibronic coupling constants. They are non-zero only if the product of irreducible representations of the wave functions of the ground and excited states contains the irreducible representation of the displacement Q.
It was proved analytically and confirmed by a series of numerical calculations (see in [3] [4] [5] ) that for any molecular system in the high-symmetry configuration K0 > 0. This means that the negative value of the curvature and, therefore, structural instabilities and distortions of high-symmetry nuclear configurations are only due to the vibronic contribution Kv. The instability takes place if the inequality
or (4)
holds.
In the simplest two-level problem, when only one nondegenerate excited state contributes significantly to the instability of the ground state, we get the following secular equation for the two states (the energy is read of the ground state level):
(5)
where K0 and K1 are the primary force constants in the ground and excited states, respectively.
The solution of this 2 × 2 equation is straightforward:
(6)
Direct calculation of the vibronic constants F and Ki involved in this PJT model is rather difficult mathematically. Usually, the values of the parameters are estimated by fitting the solutions of the secular equations to the ab initio calculated energy profiles along the coordinate of instability. In the more complex case of the three-level problem, when two excited states are active in the PJT mixing, the matrix equation is
(7)
Here K0, K1, and K2 are the primary force constants for the ground and two excited states, respectively, Δ01, and Δ02 are the energy gaps between the ground and the two excited states, and F01 and F02 are the corresponding vibronic coupling constants,
and . (8)
The constants a, b, c, f, and g are simplifying denotations. Solving for the 3×3 secular determinant, one can get the following equation for the energies of the three states (1 ground state and 2 excited states) along the distortion coordinate:
(9)
A similar equation can also be obtained for the four-level PJT problem. The procedure for estimating the vibronic constants in these cases can be found in the works [10] [13] .
Note that Equations (5)-(7) are correct for small Q values only; they characterize the changes in the K values induced by the term interactions under the Q displacements.
For a qualitative interpretation of phenomena related to the PJTE, it is worthwhile to use a more visual orbital scheme that provides information on the role of individual orbitals in the origin of instability. First of all we note that in Equation (1) ∂H/∂Q = ∂V/∂Q where V is the part of the Hamiltonian that depends on the nuclear coordinates
(10)
Here N is the number of atoms, Zα are the nuclear charges, and Rα and ri are the nuclear and electron coordinates respectively. Further, assume that the wavefunction of the excited state Ψi is the Slater determinant which differs from that of the ground state just by one-electron excitation α → m from the double occupied MO |φαñ to the unoccupied MO |φmñ. Then, the vibronic coupling constant F0i in Equation (3) can be simply expressed by means of the off-diagonal orbital vibronic coupling constant (OVCC) :
, , (11)
and are nonzero only if the product of symmetries of the two MOs |φαñ and |φmñ contains the symmetry of distortion Q. If |φαñ is the single occupied MO then
(12)
Thus, a complicated PJT problem involving many excited states can be reduced to the study of the orbital pairs which are mixed by distortion thereby destabilizing the ground state.
3. Suppression of the PJTE by Oxidation. Possibility of Planarization of 1,4-Dithiine Containing Compounds
The reference nuclear configuration of all the considered systems from this group of compounds (see Introduction) is a planar structure of D2h symmetry. In this configuration they have one imaginary frequency corresponding to the out-of-plane distortion of b1u symmetry that leads to the C2v butterfly-like equilibrium geometry [10] [11] [15] . This means that the planar structure is unstable with respect to the symmetrized b1u displacements (note that this distortion is of b1u-type if the symmetry axis of the second order is perpendicular to the plane of the molecule [11] , but if it lies in the molecular plane, then the same distortion is qualified as of b3u-type [10] [15] ). The ground electronic state of all the molecules is the 1Ag one. According to the PJTE (Equation (3)) the excited states that cause the instability of the ground state should have the 1B1u symmetry (Ag × B1u = b1u). In all the systems there is only one low-lying 1B1u excited state. Therefore, in the studied compounds we have a two-level (Ag + B1u) Ä b1u PJTE problem. An exception is the C6S8 molecule in which three excited states of Au symmetry contribute to the instability of the ground state trough the four-level (Ag + 1Au + 2Au + 3Au) Ä au PJTE problem [13] .
Then the energy profiles (cross-sections of the APES) along the coordinate of instability b1u were calculated for the ground and the B1u excited states. The vibronic coupling constants were estimated by means of fitting the solutions of the 2 × 2 secular equations (Equation (6)) to the corresponding energy profiles. Thus obtained numerical values of the PJTE parameters allow one to verify the condition of PJTE instability (4). Indeed, for small values of Q the expression for the energy can be approximately written as
(13)
Substituting in this formula the numerical data from the works [10] [11] [15] , one can see that in all the cases the resulting values of the curvature K is negative. Thus, we can conclude that the instability of the high-symmetry D2h nuclear configuration of the 1,4-dithiins with respect to the b1u puckering modes and their distortions are due to the PJT mixing of the ground 1Ag and the first excited 1B1u states.
In all the considered 1,4-dithiins these 1B1u excited states are mainly formed by one-electron excitations from the HOMO b1u to the unoccupied ag MO. Then the removal of an electron from this orbital reduces by half the PJTE negative contribution Kv to the curvature of the APES compared with a neutral molecule. Indeed, as follows from Equations (11) (12), the vibronic contribution to the curvature for the neutral molecules is approximately equal to , whereas for the radical cations where .
The decrease in the vibronic contribution leads to a positive value for the curvature K of the APES, indicating that the cations of 1,4-dithiine containing compounds should have a planar nuclear configurations. To verify this statement, we have performed calculations of the oxidized molecules, which have shown the absence of any imaginary frequency in the ground state of their planar configuration, that is, the planar geometry of the cations is an equilibrium one.
Thus, one can conclude that bending of all the considered 1,4-dithiine containing molecules is due to the PJT coupling between the ground Ag and the excited B1u states and restoration of their planar nuclear configurations upon oxidation is directly related to the decrease in the orbital vibronic coupling between these states, and hence, suppression of the PJTE.
4. Enhancement of the PJTE Distortions by Reduction. S-S Bond Cleavage in 1,2-Dithiine Containing Molecules
In [24] 3,8-diiodo-dibenzo[1,2]dithiine was investigated both theoretically and experimentally as a potential molecular system which can act as a memory storage bank. It was shown that the neutral molecule is slightly twisted around the central axis whereas two-electron reduction of this compound causes S-S bond cleavage and significant structural rearrangement [24] . Earlier we have studied two tricyclic species, the neutral carbon sulfide C6S8 and its dianion C6S82− containing two S-atoms in the 1,2-positions of the central six-membered ring and one thione (C=S) bond in the five-membered rings on its either side. We have shown [11] that in both C6S8 and systems the out-of-plane distortions are due to the PJT coupling between the ground 1A1 and two excited electronic states of 1A2 symmetry and that reduction of C6S8 up to leads to enhancement of the PJTE and as a result, to a much stronger distortion of the dianion compared with the neutral molecule. In the present paper we present the results of the electronic structure and PJTE investigation of dibenzo[1,2]dithiine molecule, C12H8S2.
For this purpose the electronic structure calculations and vibrational frequency analysis for C12H8S2 and (C12H8S2)2− molecules were carried out in their reference planar nuclear configuration of C2v symmetry. In both cases, the calculations have shown the presence of one imaginary frequency of a2 symmetry with the values of 146.3 cm−1 and 236.7 cm−1 for C12H8S2 and (C12H8S2)2−, respectively. This means that the planar configuration is unstable with respect to the symmetrized out-of-plane a2 displacement of the atoms. The calculations give also the directions and relative values of displacements (Figure 1 ).
Both systems have a nondegenerate ground electronic state 1A1. Therefore, only the excited states of 1A2 symmetry can produce the instability of the ground state (Equation (3)). In Figure 2 the calculated energy profiles (cross sections of APES) for the ground 1A1 and the low-lying excited 1A2 states of C12H8S2 and (C12H8S2)2− molecules along the instability coordinate a2 are presented. In the neutral C12H8S2 compound the first 11A2 state (∆ = 6.36 eV) is formed by one-electron excitation , while the 21A2 state corresponds to the excitation . This 21A2 state gives only a slight negative contribution to the curvature of the APES firstly due to the large energy gap (8.05 eV) and, secondly, because of small value of the vibronic constant (F02 = 0.51 eV/Å). In the dianion (C12H8S2)2− the first excited 11A2 state does not contribute to the instability of the ground state. Although the energy gap is only 2.5 eV, the vibronic constant is very small (F01 = 0.23 eV/Å) due to the fact that the mixed orbitals are localized in different parts of the molecule (Figure 2). Therefore, in both cases we can assume that the two-level PJTE problem is adequate for describing the instability of the ground state.
By fitting the solutions of the secular Equations (5) to the ab initio calculated energy profiles along the coordinate of instability we can estimate the values of the PJTE parameters. As a result we obtain: for the neutral molecule K0 = 0.69 eV/Å2, F01 = 1.56 eV/Å, ∆ = 6.36 eV, and according to Equation (13) the resulting value of the curvature K = −0.075 eV/Å2; for the dianion K0 = 0.63 eV/Å2,
Figure 1. Out-of-plane a2 normal mode in planar C2v configurations for (a) the neutral C12H8S2 and (b) the dianion form (C12H8S2)2−; (c) and (d) are the optimized twisted C2 structures for C12H8S2 and (C12H8S2)2−, respectively. The arrow lengths show expected relative (not absolute) displacements.


Figure 2. Ab initio calculated energy profiles (cross sections of the APES) along the coordinate of instability a2 for the ground A1 and the excited A2 electronic terms of (a) the neutral C12H8S2 molecule and (b) its reduced form (C12H8S2)2−.
F02 = 1.51 eV/Å, ∆ = 5.52 eV, and K = −0.196 eV/Å2. We see that the absolute value of the curvature for the reduced form estimated via the PJTE is almost two and a half times larger than this value for the neutral molecule. Thus, the reduction of the C12H8S2 molecule enhances significantly the PJTE and, as a consequence, enhances the distortions induced by it.
It should be noted that reduction does not always lead to enhancement of the PJTE and to an increase of the PJTE-induced distortions. In those cases when the excited state which is active in the PJTE is formed by excitation to the lowest unoccupied molecular orbital, the population of the latter in the process of reduction leads to suppression of the PJT effect and to the planarization of the distorted molecule. One such example is a cyclic molecule P6 which is distorted in a free state but it becomes planar being coordinated in the triple-decker sandwich complexes CpMoP6MoCp due to the transfer of the electron density from the metal to the lowest unoccupied MO of P6 molecule [7] .
5. Change in the PJTE by Chemical Substitutions. Puckering and Planarization of 1,4-Dithiine and Its S-Oxygenated Derivatives
In [11] , it was shown that chemical substitution of any atoms in heterocyclic compounds can lead both to suppression of the PJTE and planarization of heterocycles and to its enhancement resulting in the PJTE induced symmetry breaking. So, for example, the anthracene molecule (An) in its ground electronic state has a planar nuclear configuration of D2h symmetry. In this configuration it does not have any low-lying excited states of B1u symmetry which produce the PJTE instability with respect to the folding of the molecule. In comparison, the substituted 9,10-dihydroanthracene (9, 10-H2An) has a folded geometry of C2v symmetry. The addition of two hydrogen atoms in this system leads to the appearance of a new excited B1u state, the vibronic mixing of which with the ground state results in the enhancement of the PJTE and the distortion [11] . On the other hand, substitution of carbon atoms at the 1, 4, 6, and 9 positions in thianthrene molecule by more electronegative nitrogen atoms suppresses the PJTE due to increasing the energy gap between the ground and the excited electronic state responsible for the distortion that leads to planarization of the C12H8S2N4 molecule [11] .
A similar suppression of the PJTE was shown to take place in the S-oxygenated derivative of 1,4-dithiine, C4H4(SO2)2, which are planar [13] . The absence of the butterfly-type puckered structure in this molecule is explained by a significant increase of the energy gap between the ground and the PJT active excited states and by very small value of the vibronic coupling constant. The condition of instability is not satisfied and the system remains planar [13] . At the same time, DFT calculations have shown that the S-oxygenated derivatives of 1,4-dithiine with one and two SO groups are puckered and have a shadow boat conformation [25] . Below we demonstrate that the puckering of these molecules and planarization of the systems with the SO2 groups are due to enhancement and suppression of the PJTE.
For this purpose we studied a series of six molecules: 1,4-dithiine and five its oxygenated derivatives. Starting with the planar configuration, ab initio calculations of the electronic structure and vibrational frequencies of the systems in their high-symmetry nuclear configurations were carried out. One can see from Figure 3 that molecules with one and two SO2 groups have a planar conformation (no imaginary frequency), while the other four compounds have an imaginary frequency of b1u/b1 symmetry. This means that the planar nuclear configurations of these molecules are unstable and undergo symmetry breaking along the normal coordinates Q(b1u/b1) transforming the planar D2h/C2v structures to the bending C2v/C2 ones. The calculations give also the directions and relative values of these displacements (Figure 3).
All the considered molecules have a nondegenerate ground electronic states, 1Ag in systems with D2h reference configuration and 1A1 for molecules with C2v planar nuclear configuration (Figure 4). According to Equation (3), the excited
Figure 3. Puckering b1u/b1 normal modes in the series of 1,4-dithiine and S-oxygenated derivatives; the arrow lengths show expected relative (not absolute) displacements. Optimized structures (C2v/Cs configurations) are shown in two projections. In C4H4SS and C4H4SO2SO2 with the reference configuration of D2h symmetry, the z-axis is perpendicular to the plane of the molecules. In other systems with planar reference configurations C2v, the z axis passes through the sulfur atoms, and the molecules lie in the yz plane. The designation of molecules is the same as in [25] .
Figure 4. Relative energies of the ground and excited states (in eV) of 1,4-dithiine (C4H4SS) and its S-oxygenated derivatives obtained by ab initio calculations at CAS (10, 10)/6-31+G(d, p) level in the optimized D2h (C2v) geometry.
states which produce the instability of the ground state should have the B1u/B1 symmetry. It can be seen from Figure 4 that the addition of oxygen atoms to the systems significantly changes the number and energies of these excited states.
In 1,4-dithiine molecule, the main vibronic contribution to the instability comes from only one low-lying excited B1u state which is formed by one-electron excitation from the HOMO b1u to the (LUMO + 4) ag (Figure 4 and Figure 5). The values of the PJT parameters we obtained are: K0 = 0.37 eV/Å2, ∆ = 6.77 eV, and F = 1.32 eV/Å. They agree rather well with those calculated in [10] . At small distortions, the resulting value of the curvature of the AP along the b1u puckering coordinate is negative, K = −0.14 eV/Å2. Hence the condition of puckering instability (Equation (4)) is fully satisfied.
Passing to the C4H4(SO2)S and C4H4(SO2)2 molecules, one can see that the energy gaps between the ground and the excited B1/B1u states significantly increase (Figure 4). The second reason for suppression of the PJTE is a significant decrease in the vibronic coupling constants (F = 0.76 eV/Å and F = 0.04 eV/Å for the first and the second molecules, respectively). From Equation (11) it follows that for the C4H4(SO2)S molecule and for the C4H4(SO2)2 one. Since the highest occupied b1 MO in the first molecule and b1u MO in the second one have a zero value at one and, respectively, at both sulfur atoms (Figure 5 and Figure 6), this leads to a decrease in the values of the
Figure 5. MO energy levels schemes for 1,4-dithiine and its S-oxygenated derivatives in the ground Ag (A1) states in optimized D2h (C2v) geometry with indication of the one-electron excitations to the B1u (B1) terms.
Figure 6. Combinations of the occupied and unoccupied molecular orbitals for all the compounds, which give the excited B1u (B1) states. H, H − 1, H − 2, H − 3, H − 4, L, L + 1, L + 2, L + 3 and L + 4 represent the respective HOMO, HOMO − 1, HOMO − 2, HOMO − 3, HOMO − 4, LUMO, LUMO + 1, LUMO + 2, and LUMO + 3.
orbital vibronic constants . Both these factors (an increase of the energy gaps and a decrease of the vibronic coupling constants) lead to suppression of the PJTE, the condition of Equation (4) is not satisfied, so these molecules have planar conformations.
In the derivatives with one and two SO groups, oxygen atoms bring their 2pπ electrons to the π-electron system of the heterocycle, thereby providing the appearance of additional occupied b1 MOs (HOMO-1 in Figure 5 and Figure 6). This leads to the appearance of additional excited B1 states (Figure 4) which also contribute to the instability of the ground state of planar nuclear configuration. The PJTE problem in these cases becomes the three-level one (A1 + 1B1 + 2B1) Ä b1. Following the procedure outlined in Section 1, and using calculated APES cross-sections for these compounds, we can estimate the values of the PJT parameters and the resulting values of the curvature of the APES in these cases. Such, for the C4H4SOS molecule we obtain K0 = 0.44 eV/Å2, F01 = 1.26 eV/Å, Δ01 = 5.14 eV, F02 = 1.39 eV/Å, Δ02 = 8.57 eV. At small values of Qb1 the resulting value of the curvature of the APES is equal to eV/Å2. For the C4H4SOSO molecule these values are: K0 = 0.56 eV/Å2, F01 = 1.20 eV/Å, Δ01 = 4.16 eV, F02 = 1.48 eV/Å, Δ02 = 6.42 eV, and eV/Å2. We see that the absolute values of the curvature of the APES for these molecules estimated via the PJTE are much larger than that for the 1,4-dithiine molecule. At last, in the C4H4SO2SO molecule, in comparison with the C4H4(SO2)S one, the energy gap between the ground and the excited B1 states decreases, while the value of the vibronic coupling constant becomes quite large (F = 1.38 eV/Å) due to the fact that the mixed orbitals (HOMO b1 and (LUMO + 1) a1) are localized on the OSC2 fragment of the molecule which undergoes the most significant distortion (see Figure 5 and Figure 6). This leads to the large negative contribution Kv and to negative value of the curvature of the APES, so the heterocycle is distorted.
Thus, the oxygenation of the 1,4-dithiine molecule can lead to both the enhancement of the PJTE accompanied by puckering of the heterocycles (if oxygen atoms donate their 2pπ electrons to the π-system of the heterocycle) and to the PJTE suppression and subsequent flattening of derivatives with one and two SO2 groups.
6. Conclusions
Analysis of the results of published works and the results obtained in this paper allows us to draw the following conclusions:
1) The instability of planar nuclear configurations of all the considered heterocyclic molecules and their out-of-plane distortions are due to the pseudo Jahn-Teller effect.
2) If the instability of the ground state is provided mainly by the excited state formed by one-electron excitation from the HOMO to the appropriate by symmetry unoccupied MO, the oxidation of the systems by removing electrons from this MO leads to the suppression of the PJTE. In the case of 1,4-dithiine containing molecules, this results in the restoration of planar configuration.
3) In 1,2-dithiin containing molecules, reduction leads to enhancement of the PJTE followed by S-S bond cleavage and significant structural rearrangements of the systems.
4) Changes of the PJTE in the series of 1,4-ditinin and its S-oxygenated derivatives are accompanied either by out-of-plane distortions of their heterocycles (if oxygen atoms donate their 2pπ electrons to the π-system of a heterocycle) or by their flattening in derivatives with one and two SO2 groups.
Cite this paper
Gorinchoy, N. (2018) Pseudo Jahn-Teller Effect in Puckering and Planarization of Heterocyclic Compounds. International Journal of Organic Chemistry, 8, 142-159. https://doi.org/10.4236/ijoc.2018.81010
References
- 1. Bersuker, I.B. (2016) Spontaneous Symmetry Breaking in Matter Induced by Degeneracy and Pseudodegeneracy. In: Rice, S.A. and Dinner, A.R., Eds., Advances in Chemical Physics, Vol. 160, Wiley, Hoboken, NJ, 159-208.
- 2. Bersuker, I.B. (2006) The Jahn-Teller Effect. Cambridge University Press, Cambridge, UK. https://doi.org/10.1017/CBO9780511524769
- 3. Bersuker, I.B. and Polinger, V.Z. (1989) Vibronic Interactions in Molecules and Crystals. Springer-Verlag, Berlin-Heidelberg-New York.https://doi.org/10.1007/978-3-642-83479-0
- 4. Bersuker, I.B. (2001) Modern Aspects of the Jahn-Teller Effect Theory and Applications to Molecular Problems. Chemical Reviews, 101, 1067-1114.https://doi.org/10.1021/cr0004411
- 5. Bersuker, I.B. (2013) Pseudo Jahn-Teller Effect—A Two-State Paradigm in Formation, Deformation, and Transformation of Molecular Systems and Solids. Chemical Reviews, 113, 1351-1390. https://doi.org/10.1021/cr300279n
- 6. Liu., Y., Bersuker, I.B. and Boggs, J.E. (2013) Pseudo Jahn-Teller Origin of Puckering in C4H42 + , Si4H42 + , and C4F42 + Dications. Chemical Physics, 417, 26-29.https://doi.org/10.1016/j.chemphys.2013.02.033
- 7. Ivanov, A.S., Bozhenko, K.V. and Boldyrev, A.I. (2012) On the Suppression Mechanism of the Pseudo-Jahn-Teller Effect in Middle E6 (E = P, As, Sb) Rings of Triple-Decker Sandwich Complexes. Inorganic Chemistry, 51, 8868-8872. https://doi.org/10.1021/ic300786w
- 8. Sergeeva, A.P. and Boldyrev, A.I. (2010) Flattening a Puckered Pentasilacyclopentadienide Ring by Suppression of the Pseudo Jahn-Teller Effect. Organometallics, 29, 3951-3954. https://doi.org/10.1021/om1006038
- 9. Jose, D. and Datta, A. (2012) Understanding of the Buckling Distortions in Silicene. The Journal of Physical Chemistry C, 116, 24639-24648.https://doi.org/10.1021/jp3084716
- 10. Ilkhani, A.R., Hermoso, W. and Bersuker, I.B. (2015) Pseudo Jahn-Teller Origin of Instability of Planar Configurations of Hexa-Heterocycles. Application to Compounds with C4X2 Skeletons (X = O, S, Se, Te). Chemical Physics, 460, 75-82.
- 11. Gorinchoy, N.N. and Bersuker, I.B. (2017) Pseudo Jahn-Teller Effect in Control and Rationalization of Chemical Transformations in Two-Dimensional Compounds. Journal of Physics: Conference Series, 833, 012010.https://doi.org/10.1088/1742-6596/833/1/012010
- 12. Bersuker, I.B. (2017) Manipulation of Structure and Properties of Two-Dimensional Systems Employing the Pseudo Jahn-Teller Effect. FlatChem, 6, 11-27.https://doi.org/10.1016/j.flatc.2017.10.001
- 13. Pratik, S.M., Chowdhury, C., Bhattacharjee, R., Jahiruddin, Sk. and Datta, A. (2015) Pseudo Jahn-Teller Distortion for a Tricyclic Carbon Sulfide (C6S8) and Its Suppression in S-Oxygenated Dithiine (C4H4(SO2)2). Chemical Physics, 460, 101-105.https://doi.org/10.1016/j.chemphys.2015.04.009
- 14. Pratik, S.M. and Datta, A. (2015) 1,4-Dithiine-Puckered in the Gas Phase But Planar in Crystals: Role of Cooperativity. The Journal of Physical Chemistry C, 119, 15770-15776. https://doi.org/10.1021/acs.jpcc.5b04908
- 15. Hermoso, W., Ilkhani, A.R. and Bersuker, I.B. (2014) Pseudo Jahn-Teller Origin of Instability of Planar Configurations of Hexa-Heterocycles C4N2H4X2 (X = H, F, Cl, Br). Computational and Theoretical Chemistry, 1049, 109-114.https://doi.org/10.1016/j.comptc.2014.10.007
- 16. Ilkhani, A.R. (2015) Pseudo Jahn-Teller Origin of Twisting in 3,6-Pyridazinedione Derivatives; N2C4H2Y2Z2 (Y = O, S, Se, Z = H, F, Cl, Br) Compounds. Journal of Theoretical and Computational Chemistry, 14, Article ID: 1550045. https://doi.org/10.1142/S0219633615500455
- 17. Ilkhani, A.R., Gorinchoy, N.N. and Bersuker, I.B. (2015) Pseudo Jahn-Teller Effect in Distortion and Restoration of Planar Configurations of Tetra-Heterocyclic 1,2-diazetes C2N2E4, E = H, F, Cl, Br. Chemical Physics, 460, 106-110. https://doi.org/10.1016/j.chemphys.2015.07.015
- 18. Ilkhani, A.R. (2017) The Symmetry Breaking Phenomenon in 1,2,3-Trioxolene and C2Y3Z2 (Z = O, S, Se, Te, Z = H, F) Compounds: A Pseudo Jahn-Teller Origin Study. Química Nova, 40, 491-495.https://doi.org/10.21577/0100-4042.20170029
- 19. Ilkhani, A.R. and Monajjemi, M. (2015) The Pseudo Jahn-Teller Effect of Puckering in Pentatomic Unsaturated Rings C4AE5, A = N, P, As, E = H, F, Cl. Computational and Theoretical Chemistry, 1074, 19-25. https://doi.org/10.1016/j.comptc.2015.10.006
- 20. Ilkhani, A.R. (2017) Pseudo Jahn-Teller Effect in Oxepin, Azepin, and Their Halogen Substituted Derivatives. Russian Journal of Physical Chemistry A, 9, 1743-1751. https://doi.org/10.1134/S0036024417090035
- 21. Polly, R., Werner, H.J., Manby, F.R. and Knowles, P.J. (2004) Fast Hartree-Fock Theory using Local Density Fitting Approximations. Molecular Physics, 102, 2311-2321. https://doi.org/10.1080/0026897042000274801
- 22. Hehre, W.J., Ditchfield, R. and Pople, J.A. (1972) Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. The Journal of Chemical Physics, 56, 2257-2261. https://doi.org/10.1063/1.1677527
- 23. Frisch, M.J., Trucks, G.W., Schlege, H.B., et al. (2009) Gaussian 09. Revision B.01, Gaussian, Inc., Wallingford.
- 24. Benniston, A.C., Allen, B.D., Harriman, A., Llarena, I., Rostron, J.P. and Stewart, B. (2009) Accessing Molecular Memory via a Disulfide Switch. New Journal of Chemistry, 33, 417-427. https://doi.org/10.1039/B814676D
- 25. Vessally, E. (2008) DFT Calculations on 1,4-dithiine and S-oxygenated Derivatives. Bulletin of the Chemical Society of Ethiopia, 22, 465-468. https://doi.org/10.4314/bcse.v22i3.61259






