Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 8 (2012) , Article ID: 21928 , 9 pages DOI:10.4236/ijcns.2012.58054
Large-Integer Multiplication Based on Homogeneous Polynomials
Computer Science Department, New Jersey Institute of Technology, Newark, USA
Email: verb@njit.edu
Received June 17, 2012; revised July 28, 2012; accepted August 6, 2012
Keywords: Homogeneous Polynomials; Toom-Cook Algorithm; Multidigit Integers; Multi-Stage Multiplication; Generalized Horner Rule; Large-Integer Multiplication
ABSTRACT
Several algorithms based on homogeneous polynomials for multiplication of large integers are described in the paper. The homogeneity of polynomials provides several simplifications: reduction of system of equations and elimination of necessity to evaluate polynomials in points with larger coordinates. It is demonstrated that a two-stage implementation of the proposed and Toom-Cook algorithms asymptotically require twice as many standard multiplications than their direct implementation. A multistage implementation of these algorithms is also less efficient than their direct implementation. Although the proposed algorithms as well as the corresponding Toom-Cook algorithms require numerous algebraic additions, the Generalized Horner rule for evaluation of homogeneous polynomials, provided in the paper, decrease this number twice.
1. Introduction and Basic Definitions
Crypto-immunity of various protocols of secure communication over open channels is based on modular arithmetic of large integers with hundreds of decimal digits. Multiplications and exponentiations of large integers are essential operations in this arithmetic. Yet, standard programming libraries in general-purpose computers handle multiplication of integers A and B if the number of decimal digits in each does not exceed m. Such integers we will refer to as standard integers. For instance, if a computer cannot multiply integers larger than 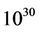 without a specially-written program, then in this case m = 30.
without a specially-written program, then in this case m = 30.
The first papers on multiplication of large integers were published by Karatsuba-Ofman [1] and by Toom [2]. Several years later Toom’s scheme was improved by Cook {see [3,4]}. Analysis of computational complexity of Toom-Cook algorithm (TCA) is provided in [5] and theoretical foundation for efficient multiplication of large integers is discussed in [6]. An efficient implementation of the TCA in cryptographic systems is described in several patents [7]. Analysis of computational complexity of the TCA and its lower bound is provided in [8].
A special case of the TCA, where one multiplier is significantly larger than another, is considered in [9].
Consider two nm-digit-large integers 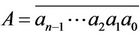 and
and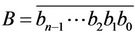 , where every part
, where every part 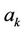 and
and 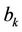 is a m-decimal-digit large standard integer {SI, for short}. Let us represent A and B as
is a m-decimal-digit large standard integer {SI, for short}. Let us represent A and B as
 ; (1.1)
; (1.1)
and
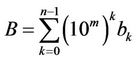 . (1.2)
. (1.2)
Therefore, the product C = AB is expressed as
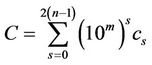 ; (1.3)
; (1.3)
where 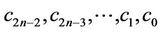 are
are  unknown coefficients.
unknown coefficients.
In order to compute the product C, these coefficients must be determined.
Example 1.1: Suppose we need to multiply two integers A = 385,495,374,109;
and B = 608,348,696,284;
using a computing device that cannot multiply integers of order higher than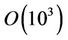 . Therefore, in this example m = 3 and we split A and B into n = 4 parts, where
. Therefore, in this example m = 3 and we split A and B into n = 4 parts, where

The algorithm provided in Section 2 demonstrates how to solve this problem by using a minimal number of multiplications of m-digit SIs.
2. Multiplication C = AB Based on Homogeneous Polynomials
Consider two n-th degree homogeneous polynomials of two integer variables x and y:
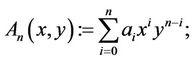 (2.1)
(2.1)
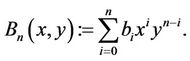 (2.2)
(2.2)
Let
 (2.3)
(2.3)
Remark 2.1: All coefficients in polyno-mials 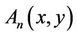 and
and 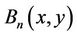 are inputs, and the coefficients in
are inputs, and the coefficients in 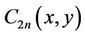 are outputs.
are outputs.
For short, the multiplication algorithm, based on homogeneous polynomials (HP), provided below is called the AHP.
First of all, definition (2.3) implies that
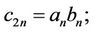 and
and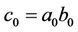 .(2.4)
.(2.4)
Computation of the remaining  coefficients in (2.3) is described in the algorithm. Prior to that, let us modify Equation (2.3) for integers
coefficients in (2.3) is described in the algorithm. Prior to that, let us modify Equation (2.3) for integers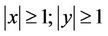 .
.
Consider
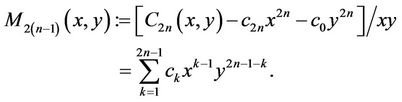 (2.5)
(2.5)
As is shown in Section 3, we can easily separate “odd” 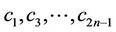 and “even”
and “even”  unknown coefficients.
unknown coefficients.
The following properties of homogeneous polynomials imply certain limitations on choice of evaluation points:
Property 1: If n is a degree of homogeneity of  and g is a non-zero real number, then
and g is a non-zero real number, then
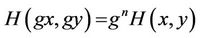 . (2.6)
. (2.6)
Therefore, if , then
, then
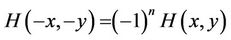 . (2.7)
. (2.7)
Property 2: If the degree of homogeneity is even, then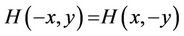 ;
;
otherwise
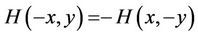 . (2.8)
. (2.8)
Corollary 1: Definition (2.3) implies that
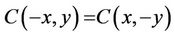 ; (2.9)
; (2.9)
since for every integer n  has an even degree of homogeneity.
has an even degree of homogeneity.
Corollary 2: Identity (2.9) implies that it is not advantageous to consider, for instance, both 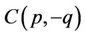 and
and ; neither it is advantageous to consider
; neither it is advantageous to consider  and
and 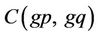 for any non-zero integer g (2.6). Therefore, in this paper are considered only relatively prime pairs of integers p and q.
for any non-zero integer g (2.6). Therefore, in this paper are considered only relatively prime pairs of integers p and q.
3. Separation of “Even” and “Odd” Coefficients in AHP
Step 3.1: Compute sums
 (3.1)
(3.1)
for the first 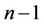 relatively prime pairs of integers
relatively prime pairs of integers
 (3.2)
(3.2)
Remark 3.1: Using (3.1) and (3.2), we create and solve  equations with
equations with 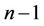 “even” unknowns
“even” unknowns 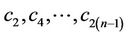 .
.
Step 3.2: Compute differences
 (3.3)
(3.3)
for the same pairs

Remark 3.2: As a result, in (3.3), we create  equations with n unknowns
equations with n unknowns .
.
Since by this time the values of all “even” coefficients 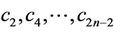 are already computed, we use
are already computed, we use  (3.5) as the n-th equation for computation of n “odd” coefficients.
(3.5) as the n-th equation for computation of n “odd” coefficients.
The following example illustrates a slightly different approach to separate “even” and “odd” variables.
3.1. Separation of Unknowns: n = 5
First, compute 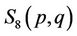 {see (3.1)} for
{see (3.1)} for 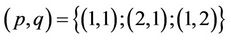 and from three equations find
and from three equations find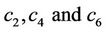 ; second, compute
; second, compute 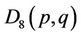 {see (3.3)} for
{see (3.3)} for 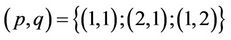 and derive three equations with four “odd” unknowns
and derive three equations with four “odd” unknowns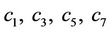 . As the fourth (“missing”) equation, we consider
. As the fourth (“missing”) equation, we consider
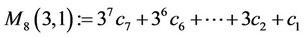 ; (3.4)
; (3.4)
{see (2.5)}. After all “even” coefficients are computed, let
 . (3.5)
. (3.5)
Finally we derive the fourth equation
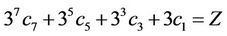 . (3.6)
. (3.6)
3.2. AHP for Multiplication of Triple-Large Integers
Let us consider a multiplication of triple-large integers; let
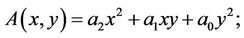
and
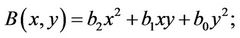
therefore
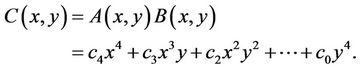 (3.7)
(3.7)
Step 3.1:
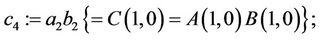 (3.8)
(3.8)
Step 3.2:
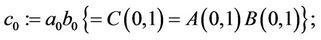 (3.9)
(3.9)
Step 3.3:
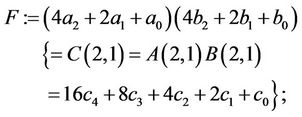 (3.10)
(3.10)
Step 3.4:
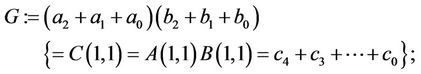 (3.11)
(3.11)
Step 3.5:
 (3.12)
(3.12)
Step 3.6:
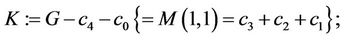 (3.13)
(3.13)
Step 3.7:
 (3.14)
(3.14)
Step 3.8:
 (3.15)
(3.15)
Remark 3.3: From the system of linear Equations (3.13)-(3.15) we determine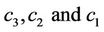 .
.
Step 3.9:
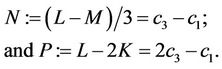 (3.16)
(3.16)
Step 3.10:
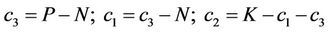 (3.17)
(3.17)
The algorithm described in (3.8)-(3.17) requires 24 algebraic additions.
4. Reduction of Algebraic Additions
Let us consider a multiplication of two quatro-large integers
 and
and 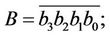
where every part 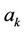 and
and  is a m-decimal-digit large SI [2].
is a m-decimal-digit large SI [2].
Let us represent A and B as
 (4.1)
(4.1)
and
 (4.2)
(4.2)
Therefore, the product C = AB can be expressed as
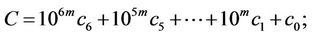 (4.3)
(4.3)
where seven coefficients  must be determined.
must be determined.
The drawback of the TCA and AHP algorithms is the large number of required algebraic additions. The following algorithm shows how to decrease twice the number of these additions.
Step 4.0:
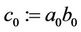 ;
;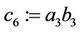 ; (4.4)
; (4.4)
Step 4.1:
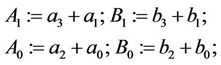 (4.5)
(4.5)
Step 4.2:
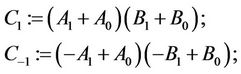 (4.6)
(4.6)
Step 4.3:
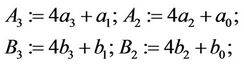 (4.7)
(4.7)
Step 4.4:
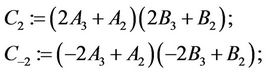 (4.8)
(4.8)
Step 4.5:
 (4.9)
(4.9)
Step 4.6:
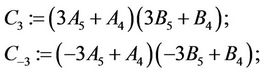 (4.10)
(4.10)
Remark 4.1: For every k the variables  and
and 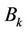 are used twice {see (4.6)-(4.10)}. In order to decrease the amount of computation, we pre-compute them only once. Therefore, we reduce twice the number of algebraic additions in (4.6)-(4.10).
are used twice {see (4.6)-(4.10)}. In order to decrease the amount of computation, we pre-compute them only once. Therefore, we reduce twice the number of algebraic additions in (4.6)-(4.10).
Step 4.7:
 (4.11)
(4.11)
Step 4.8:
 (4.12)
(4.12)
Step 4.9:
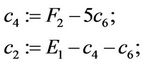 (4.13)
(4.13)
Step 4.10:
 (4.14)
(4.14)
Step 4.11:
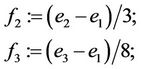 (4.15)
(4.15)
Step 4.12:
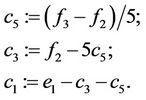 (4.16)
(4.16)
This algorithm computes the product C = AB using seven multiplications of SIs instead of sixteen such multiplications as required by “grammar-school” rules. For more details on the AHP of quatro-large integers see Sections 8 and 9.
5. Comparison of Evaluated Polynomials in TCA vs AHP
First of all, in the TCA
 ; (5.1)
; (5.1)
are computed, and in the AHP
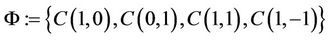 (5.2)
(5.2)
are computed. Additional values of evaluated polynomials for 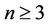 are provided in Table 1.
are provided in Table 1.
Remark 5.1: Observe the fast growth of the values of evaluation points in the TCA in comparison with corresponding points in the AHP.
The sets  and
and 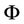 of polynomial evaluations in Table 1 are defined in (5.1) and (5.2).
of polynomial evaluations in Table 1 are defined in (5.1) and (5.2).
6. Comparison of TCA vs AHP for n = 6
6.1. AHP Framework
Compute
 (6.1)
(6.1)
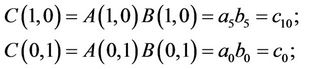 (6.2)
(6.2)
Computation of  and
and  has the same complexity as
has the same complexity as  in the TCA; and computation of
in the TCA; and computation of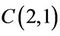 ;
; ;
; 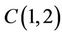 and
and 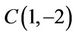 has the same complexity as
has the same complexity as 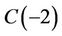 in the TCA {see Table 1). For instance,
in the TCA {see Table 1). For instance,
 (6.3)
(6.3)
where all coefficients are merely binary shifts. Furthermore, computation of ;
; ; and
; and 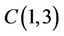 has the same complexity as
has the same complexity as  in TCA, {Table 1}.
in TCA, {Table 1}.
6.2. Toom-Cook Algorithm
Compute

Table 1. Points of polynomial evaluation in TCA and AHP.
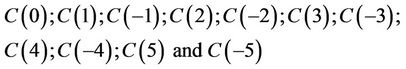 (6.4)
(6.4)
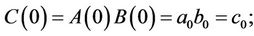 (6.5)
(6.5)
 (6.6)
(6.6)
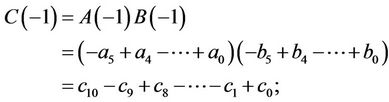 (6.7)
(6.7)
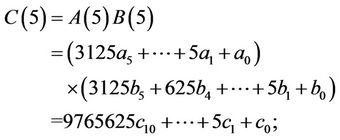 (6.8)
(6.8)
where both  and
and 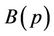 can be computed by Horner Rule [10].
can be computed by Horner Rule [10].
7. AHP for n = 7
It is easy to see that
 , (7.1)
, (7.1)
i.e., we need to compute thirteen remaining coefficients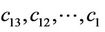 .
.
Let
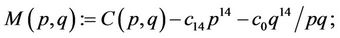 (7.2)
(7.2)
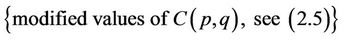
In order to separate “odd” and “even” unknowns, compute
 (7.3)
(7.3)
In general, by computing
 (7.4)
(7.4)
for  we create six equations with six “even” unknowns
we create six equations with six “even” unknowns .
.
Analogously, by computing
 (7.5)
(7.5)
for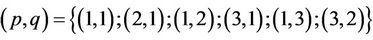 , we create six equations with seven “odd” unknowns
, we create six equations with seven “odd” unknowns .
.
After the values of ”even” coefficients 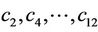 are computed, we use
are computed, we use 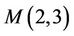 {see (7.2)} as the seventh equation for computation of all “odd” coefficients.
{see (7.2)} as the seventh equation for computation of all “odd” coefficients.
8. AHP for n = 4 in Details
Consider
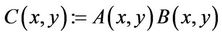 ; (8.1)
; (8.1)
where
 ; (8.2)
; (8.2)
 ; (8.3)
; (8.3)
and
 ; (8.4)
; (8.4)
then
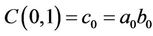 ;
; ; (8.5)
; (8.5)
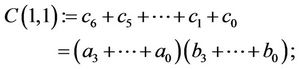 (8.6)
(8.6)
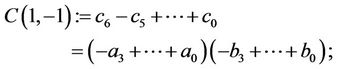 (8.7)
(8.7)
 (8.8)
(8.8)
 (8.9)
(8.9)
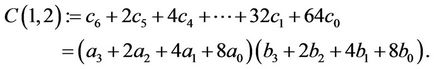 (8.10)
(8.10)
9. Solution of System of Equations (8.6)-(8.10)
Step 9.1: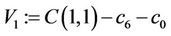 ;
;
Step 9.2: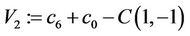 ;
;
Step 9.3: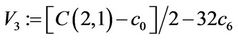 ;
;
Step 9.4: ;
;
Step 9.5: .
.
Remark 9.1: Using V1-V5, we find five unknowns 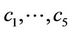 from five linear equations:
from five linear equations:
 ; (9.1)
; (9.1)
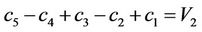 ; (9.2)
; (9.2)
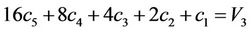 ; (9.3)
; (9.3)
 ; (9.4)
; (9.4)
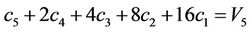 . (9.5)
. (9.5)
Step 9.6:
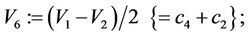 (9.6)
(9.6)
Step 9.7:
 . (9.7)
. (9.7)
Step 9.8:
 (9.8)
(9.8)
Step 9.9:
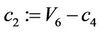 . (9.9)
. (9.9)
Step 9.10:
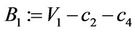 ;
; ;
; .
.
Remark 9.2: Now we solve the system of three equations with three unknowns:
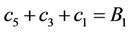 (9.10)
(9.10)
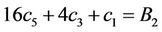 (9.11)
(9.11)
 (9.12)
(9.12)
Step 9.11:
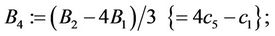 (9.13)
(9.13)
Step 9.12:
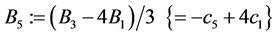 (9.14)
(9.14)
Step 9.13:
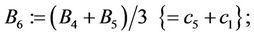 (9.15)
(9.15)
Step 9.14:
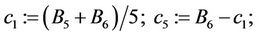 (9.16)
(9.16)
Step 9.15:
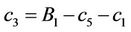 (9.17)
(9.17)
10. Multistage Implementation of TCA and AHP
10.1. Two-Stage Implementation (TSI)
Let us consider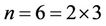 , and analyze how to multiply sextuple-large integers in two stages. On the first stage, we represent A and B as double long:
, and analyze how to multiply sextuple-large integers in two stages. On the first stage, we represent A and B as double long:
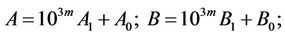 (10.1)
(10.1)
and compute AB applying the Karatsuba algorithm [1], which requires three multiplications of 3m-long integers.
Then, as the second stage, we compute every product of triple-long integers using either the TCA or AHP each requiring five standard multiplications {SMs, for short}. Therefore, the two-stage implementation requires fifteen SMs rather than eleven SMs required by the TCA or by AHP. Table 2 provides comparison for several other cases, where
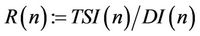 (10.2)
(10.2)
General case: Let us now analyze the two-stage implementation of a multiplication algorithm if n = rs.
First, we represent A and B as
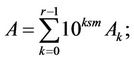 (10.3)
(10.3)
and
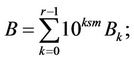 (10.4)
(10.4)
Such an implementation requires  multiplications each of sm-long integers. Then, on the second stage, we multiply sm-long integers. Every such multiplica-tion requires
multiplications each of sm-long integers. Then, on the second stage, we multiply sm-long integers. Every such multiplica-tion requires 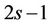 SMs. Therefore, we need
SMs. Therefore, we need
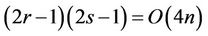 (10.5)
(10.5)
SMs in total. However, the direct (one-stage) multiplication requires only
 (10.6)
(10.6)
It is easy to verify that both parts in the inequality
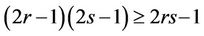 (10.7)
(10.7)
are equal if and only if either r = 1, or s = 1, or r = s = 1. In all other cases

Table 2. Number of SMs in two-stage (TSI) and direct implementation (DI).
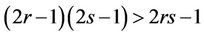 (10.8)
(10.8)
Thus, the TSI of either the TCA or AHP for large r and s asymptotically requires twice as many SMs than the DI.
Example 10.1: Now let m = 4;
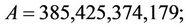
and
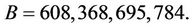
Therefore, in this example we need to split A and B into three parts, i.e., n = 3.
By the algorithm, described in Sections 8 and 9 we can compute C = AB using five multiplications of four-digit large integers. However, if the standard integers are only two-digit long, we can pre-compute each product recursively using the Karatsuba algorithm. Each of these five products requires three SMs, i.e., overall we need fifteen SMs to compute C = AB. On the other hand, we can compute the same product AB splitting both A and B into six parts.
In this case m = 2. To compute AB, we need only eleven SMs by using the direct implementation vs fifteen SMs required in the recursive TSI implementation.
10.2. Multi-Stage Implementation
Let now . Therefore, we multiply A and B in either three stages using the Karatsuba algorithm [1] or using the AHP or TCA directly. In the MSI we need
. Therefore, we multiply A and B in either three stages using the Karatsuba algorithm [1] or using the AHP or TCA directly. In the MSI we need 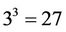 SMs; while in the DI we need only fifteen SMs.
SMs; while in the DI we need only fifteen SMs.
Remark 10.1: Since the number of algebraic additions in the DI asymptotically grows as function of n, it is essential to properly select the evaluation points  to implement symmetricity illustrated above in Section 4 {see (4.4)-4.16)} and to simplify computational complexity stemming from the multiplication by constant coefficients. These issues are addressed in Sections 11- 13.
to implement symmetricity illustrated above in Section 4 {see (4.4)-4.16)} and to simplify computational complexity stemming from the multiplication by constant coefficients. These issues are addressed in Sections 11- 13.
11. Number of Algebraic Additions
Notice that computation of 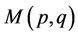 requires 2n additions of SIs. Since we need to compute
requires 2n additions of SIs. Since we need to compute  for
for 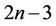 different values of
different values of , the total number of algebraic additions is of order
, the total number of algebraic additions is of order 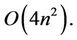 This number can be reduced twice as demonstrated in Section 2. Since every addition of m-digit long integers has order
This number can be reduced twice as demonstrated in Section 2. Since every addition of m-digit long integers has order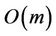 , therefore the total complexity of all additions is of order
, therefore the total complexity of all additions is of order 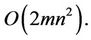 Hence, the overall complexity is equal
Hence, the overall complexity is equal
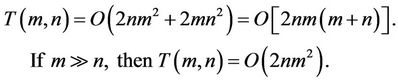 (11.1)
(11.1)
12. Analysis of TCA vs AHP
In large-integer multiplication we addressed two sources of complexity: the number of standard multiplications and the number of algebraic additions. The third source of complexity is multiplication by constant coefficients when the polynomials  and
and  are evaluated at points
are evaluated at points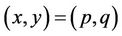 .
.
The Table 3 compares the polynomial evaluations in the TCA and AHP frameworks respectively for various values of n. It means that if n = 15, then in TCA polynomials 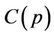 are evaluated for
are evaluated for 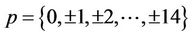 and in the corresponding AHP polynomials
and in the corresponding AHP polynomials 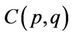 are evaluated for
are evaluated for
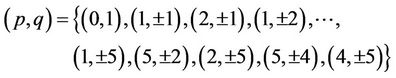
Example 12.1: Compare for n = 14 the computation of C(2,5) and C(13):
 (12.1)
(12.1)
In the next section we provide an iterative procedure that computes .
.
13. Generalized Horner Rule for Homogeneous Polynomial
Let 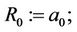
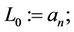 and for
and for 

Table 3. Evaluations required in Toom’s vs AHP frameworks.
 (13.1)
(13.1)
and
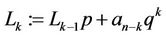 (13.2)
(13.2)
then
 (13.3)
(13.3)
Analogously, we can compute .
.
14. Values of 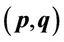 Simplifying Computation of
Simplifying Computation of 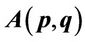 and
and 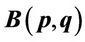
Case 1: if  and
and 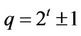 in (13.1), then
in (13.1), then 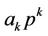 requires a binary shift on sk positions, and
requires a binary shift on sk positions, and  requires merely a binary shift on t positions and one algebraic addition [3].
requires merely a binary shift on t positions and one algebraic addition [3].
Case 2: if  and
and  in (13.2), then, analogously as in the Case1,
in (13.2), then, analogously as in the Case1,  requires a binary shift on sk positions, and
requires a binary shift on sk positions, and  requires a binary shift on t positions and one algebraic addition.
requires a binary shift on t positions and one algebraic addition.
Case 3: if  and
and  in (13.1), then it is necessary to use two binary shifts and one algebraic addition.
in (13.1), then it is necessary to use two binary shifts and one algebraic addition.
Case 4: if  and
and 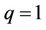 in (13.2), then, analogously as in the Case 3, it is necessary to use two binary shifts and one algebraic addition.
in (13.2), then, analogously as in the Case 3, it is necessary to use two binary shifts and one algebraic addition.
Case 5: if 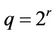 and
and 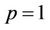 in (13.1), then it is necessary to use only one binary shift on r positions.
in (13.1), then it is necessary to use only one binary shift on r positions.
Case 6: if 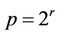 and
and 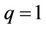 in (13.2), then, analogously as in the Case 5, it is necessary to use only one binary shift.
in (13.2), then, analogously as in the Case 5, it is necessary to use only one binary shift.
Example 14.1: In the following set of 37 points each 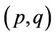 satisfies one of six special cases listed above:
satisfies one of six special cases listed above:

Add to this set the other 111 points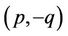 ,
, 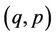 and
and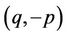 . For each of these 148 points the number of required algebraic additions in the AHPs is smaller than in the corresponding TCAs.
. For each of these 148 points the number of required algebraic additions in the AHPs is smaller than in the corresponding TCAs.
Example 14.2: If n = 22, then for the TCA we need to evaluate  at 43 points
at 43 points ,
,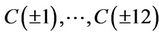 ; yet, for the AHP we evaluate polynomial
; yet, for the AHP we evaluate polynomial  at points
at points
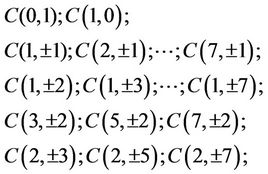
and , where, for instance, the evaluation of C(5,4) requires fewer basic operations than for C(21) in the TCA.
, where, for instance, the evaluation of C(5,4) requires fewer basic operations than for C(21) in the TCA.
15. Optimized AHP
In order to decrease twice the number of additions/subtractions, we need to adjust the Generalized Horner Rule for iterative computation of  and
and .
.
Notice that if n is odd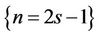 , then
, then
 (15.1)
(15.1)
Otherwise, if n is even, i.e., if n = 2s, then
 (15.2)
(15.2)
Therefore, for every even and odd n
 (15.3)
(15.3)
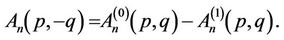 (15.4)
(15.4)
Let us show how to modify (13.1) for iterative computation of (15.1).
Consider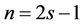 ;
;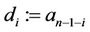 ; assign
; assign 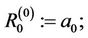
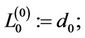 and for every
and for every  compute
compute
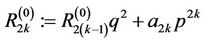 (15.5)
(15.5)
 (15.6)
(15.6)
hence,
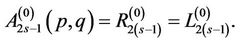 (15.7)
(15.7)
Assign 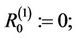

and for every 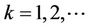 compute
compute
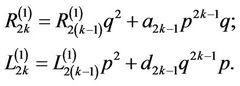 (15.8)
(15.8)
hence

Thus,
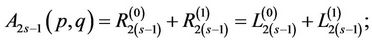 (15.9)
(15.9)
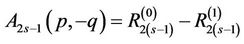 (15.10)
(15.10)
Example 15.1: Let us consider n = 7. Then
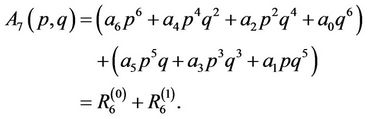
The iterative procedures (15.5)-(15.8) are simplified if 1) p is a power of 2 and  or 2) p = 1 and
or 2) p = 1 and 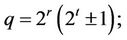 {see the corresponding Cases 1-6 in Section 13}.
{see the corresponding Cases 1-6 in Section 13}.
The Equations (13.2), (15.5) and (15.6) can be analogously modified for iterative computation of
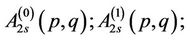
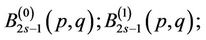
and
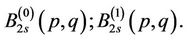
16. Conclusion
It has been demonstrated that the overhead in the ToomCook algorithm is higher than in the proposed approach based on homogeneous polynomials  and
and . Integrality of all coefficients in the TCA and AHP is demonstrated by the first author in [11].
. Integrality of all coefficients in the TCA and AHP is demonstrated by the first author in [11].
17. Acknowledgements
I deeply appreciate comments of I. V. Semushin and stylistic suggestions of Yu. Polyakov and R. Rubino that improved the quality of this paper. I wish to express my gratitude to typesetters for their patience.
REFERENCES
- A. Karatsuba and Yu. Ofman, “Multiplication of Multidigit Numbers on Automata,” Soviet Physics-Doklady, Vol. 7, 1963, pp. 595-596.
- A. Toom, “The Complexity of a Scheme of Functional Elements Realizing the Multiplication of Integers,” Soviet Mathematics-Doklady, Vol. 7, 1963, pp. 714-716.
- S. A. Cook, “On the Minimum Computation Time of Functions,” Chapter 3, Ph.D. Thesis, Harvard University, Cambridge, 1966, pp. 51-77.
- D. Knuth, “Art of Computer Programming: Seminumerical Algorithms,” 2nd Edition, Vol. 2, Addison-Wesley, New York, 1981.
- R. Crandall and C. Pomerance, “Prime Numbers: A Computational Perspective,” Springer, New York, 2001. doi:10.1007/978-1-4684-9316-0
- D. Bernstein, “Multidigit Modular Multiplication with Explicit Chinese Remainder Theorem,” 1997. ftp://koobera. math.uic.edu/pub/papers/m3.dvi
- R. Crandall, “Method and Apparatus for Public Key Exchange in a Cryptographic Systems,” US Patents 5159632, 1992; 5271061, 1993; 5463690, 1994.
- F. Ablayev and M. Karpinski, “A Lower Bound for Integer Multiplication on Randomized Ordered Read-Once Branching Programs,” Information and Computation, Vol. 186, No. 1, 2003, pp. 78-89. doi:10.1016/S0890-5401(03)00118-4
- A. Zanoni, “Iterative Toom-Cook Methods for Very Unbalanced Long Integer Multiplication,” Proceedings of the 2010th International Symposium on Symbolic and Algebraic Computation, Munich, 25 July 2010, pp. 319- 323. doi:10.1145/1837934.1837995
- W. G. Horner, “A New Method of Solving Numerical Equations of All Orders, by Continuous Approximation,” Philosophical Transactions of Royal Society of London, Vol. 109, 1819, pp. 308-335. doi:10.1098/rstl.1819.0023
- B. Verkhovsky and R. Rubino, “Corporate Intranet Security: Packet-Level Protocols for Preventing Leakage of Sensitive Information and Assuring Authorized Network Traffic,” International Journal of Communications, Network and System Sciences, Vol. 5, No. 5, 2012, pp. 517- 524.

