Int'l J. of Communications, Network and System Sciences
Vol.6 No.1(2013), Article ID:27441,6 pages DOI:10.4236/ijcns.2013.61001
Public-Key Cryptosystems with Secret Encryptor and Digital Signature
Computer Science Department, New Jersey Institute of Technology, Newark, USA
Email: verb73@gmail.com
Received October 20, 2012; revised November 28, 2012; accepted December 25, 2012
Keywords: Digital Signature; Discrete Logarithm; El Gamal Algorithm; Generator; Modular Exponentiation; Public Key Cryptosystem; Secure Communication; Sender Identification
ABSTRACT
This paper describes and compares a variety of algorithms for secure transmission of information via open communication channels based on the discrete logarithm problem that do not require search for a generator (primitive element). Modifications that simplify the cryptosystem are proposed, and, as a result, accelerate its performance. It is shown that hiding information via exponentiation is more efficient than other seemingly simpler protocols. Some of these protocols also provide digital signature/sender identification. Numeric illustrations are provided.
1. Introduction and Basic Definition
This paper describes and compares special cases of several protocols for secure transmission of information: secret key establishment [1], poly-alphabetic analogue of affine protocol [2], El Gamal cryptographic protocol [3] and an analogue of the RSA algorithm [4], which cryptoimmunity is not based on the difficulty of factorization {see EvESE algorithm in Sections 7 and 8}. The latter protocol {as well as all other protocols} is exclusively based on the difficulty of solving a discrete logarithm problem (DLP) [5,6] where the base g is a generator in modular arithmetic with a modulus p that is a safe prime.
Definition1.1: A prime integer p is called a safe prime if
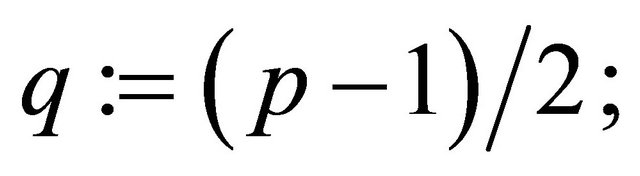 (1.1)
(1.1)
is also a prime.
Therefore, for every 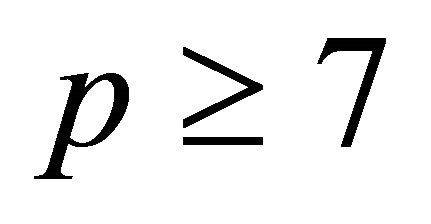 q is odd. Moreover, if p is a safe prime and
q is odd. Moreover, if p is a safe prime and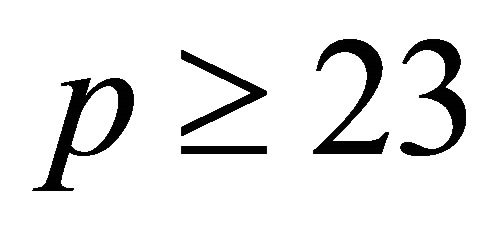 , then
, then 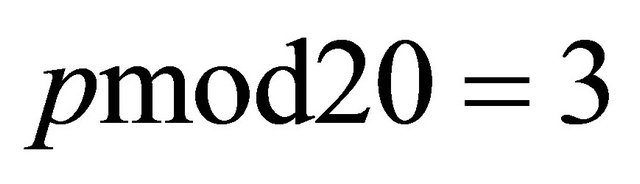 or 7 or 19.
or 7 or 19.
As it is demonstrated in [7], if p is a safe prime, then the algorithm finding a generator g is a computationally fast procedure. Some simplifications and innovations in this paper are based on the observation that 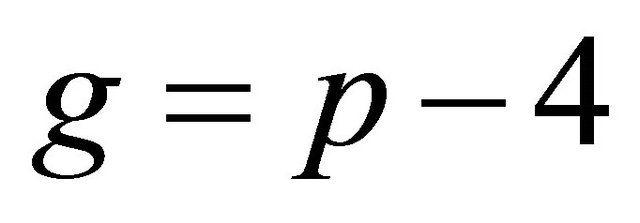 is the generator for every safe prime
is the generator for every safe prime 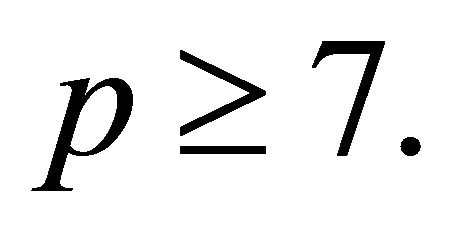
The major innovation {Encryption via Exponentiation with a secret encryptor} is provided in Section 7 and demonstrated in Section 8.
2. System Parameters
If p is a safe prime greater than or equal 7, then
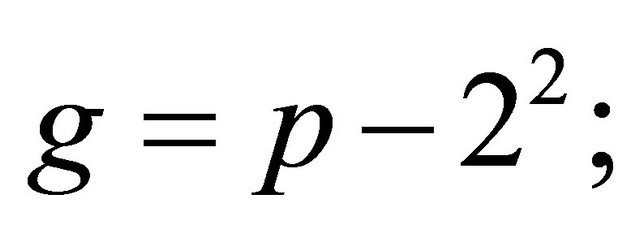 (2.1)
(2.1)
is a generator for every p. Indeed, (1.1) and the Fermat Little Theorem (FLT) [5] imply that
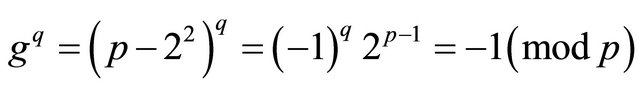 ; (2.2)
; (2.2)
and
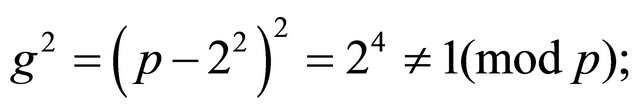 (2.3)
(2.3)
otherwise 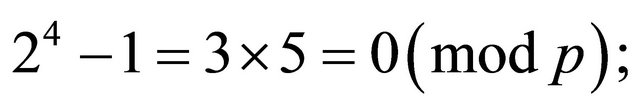 which is impossible if
which is impossible if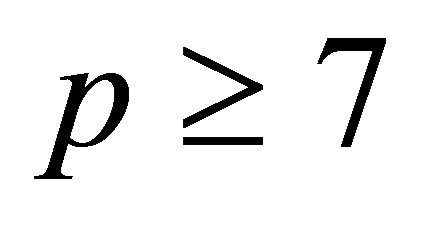 .
.
Parameters p and g are used by all participating users.
3. Establishment of Secret Encryptor
Step3.1: The sender (Alice) selects a large safe prime p and transmits it to the receiver (Bob) via an open channel;
Step3.2: Respectively, Alice and Bob randomly select large integers a and b as their private keys;
Step3.3: Alice and Bob independently compute their public keys:
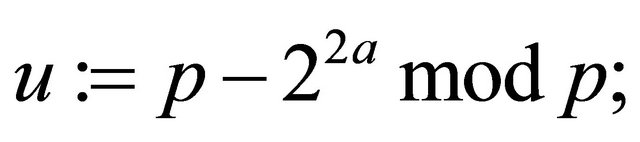 (3.1)
(3.1)
and
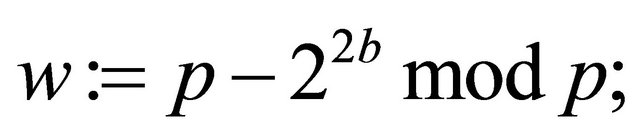 (3.2)
(3.2)
Step3.4: Using the public key of the receiver, Alice computes
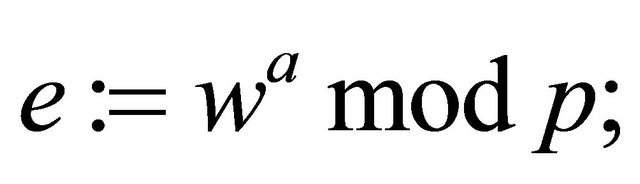 (3.3)
(3.3)
Step3.5: Using the public key of the senderBob computes
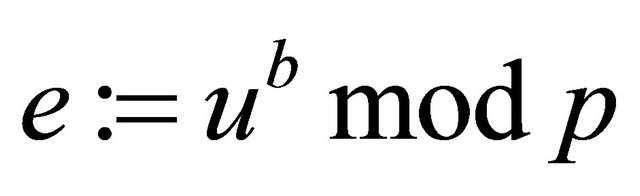 ; (3.4)
; (3.4)
where e is their mutual secret encryptor.
Remark3.1: Parameters a, b and e must be distinct from q.
4. Several Ways to Hide Information
Suppose Alice wants to send a plaintext m {which is represented in a numeric for m}, where the message m satisfies
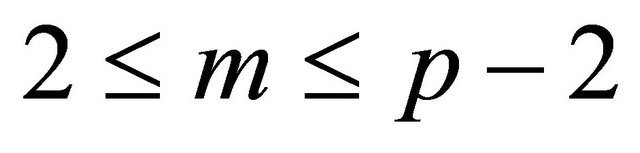 . (4.1)
. (4.1)
Encryption {Alice encrypts message m and sends it to Bob, who decrypts it}:
Remark4.1: Alice has several alternatives: she can either create a ciphertext
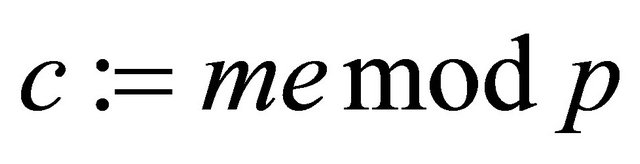 ; (4.2)
; (4.2)
which is an equivalent of the ElGamal scheme [3]; or consider
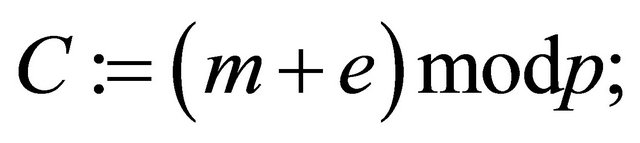 (4.3)
(4.3)
which is a poly-alphabetic shift cipher [8,9]; or she can split the secret key e into two parts  and
and 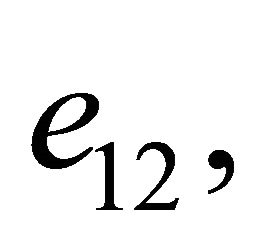 and then consider
and then consider
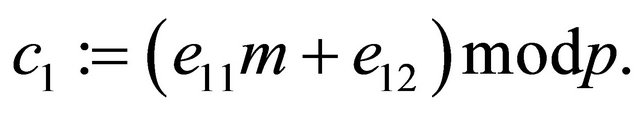 (4.4)
(4.4)
The encryption (4.4) is an equivalent of the poly-alphabetic affine algorithm [2]. Yet another option is described in Section 6.
In general, Bob can apply any ordered binary operator B: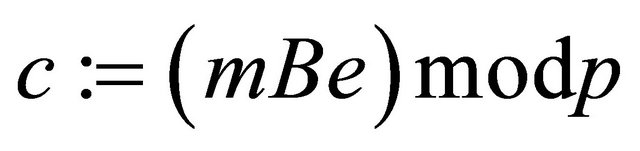 , provided that the inverse of e exists, computable and it is unique for this operator.
, provided that the inverse of e exists, computable and it is unique for this operator.
Below we describe Alice’s and Bob’s actions if (4.2) or (4.3) are used. If (4.2) is applied, Alice transmits the ciphertext c to Bob via an open channel.
Decryption: Using Alice’s public key u and his private key b, Bob computes a decryptor
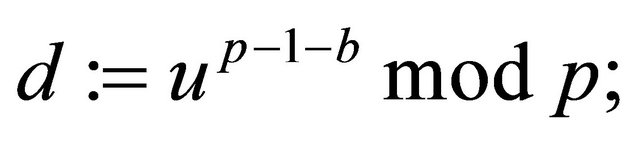 (4.5)
(4.5)
and finally, he recovers the plaintext:
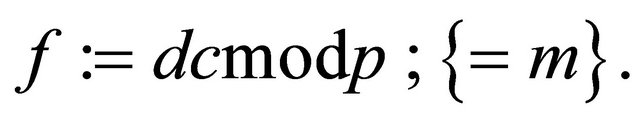 (4.6)
(4.6)
In (4.3) case the receiver computes his decryptor
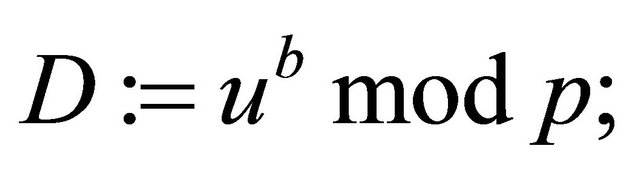 (4.7)
(4.7)
and
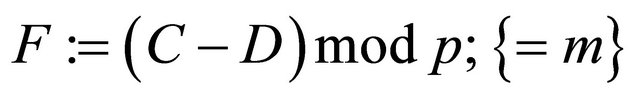 . (4.8)
. (4.8)
Furthermore, there are several ways {see (4.5) and (4.7)} to compute the decryptors d and D respectively. One requires exponentiation p−1−a and another a. In the following Example4, a=35 and p‒1‒a=837 have binary “weights” 3 and 7 respectively. Therefore, D requires fewer multiplications than d. Hence, it is faster to compute D than d. In general, it is computationally advantageous if both Alice and Bob select their secret keys a and b with “smaller” binary “weights”. However, these additional constraints provide clues for a potential intruder/ cryptanalyst.
Yet, there is an alternative algorithm for modular multiplicative inverse (AAMMI) proposed by the author of this paper in [10] and analyzed in [11]. Extensive computer experiments demonstrated that the AAMMI algorithm is computationally more efficient than (4.5); {see Tables 1-3 below}.
In spite of computational simplicity, applications of the encryptor e either in (4.2) or in (4.3) have negative sides: if at least one plaintext block, 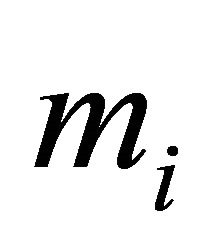 , becomes known, an intruder can deduce every plaintext
, becomes known, an intruder can deduce every plaintext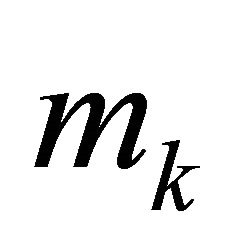 . Indeed, since (4.2) implies
. Indeed, since (4.2) implies
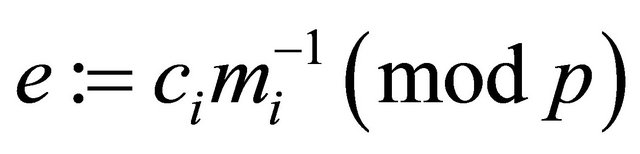 ; (4.9)
; (4.9)
then
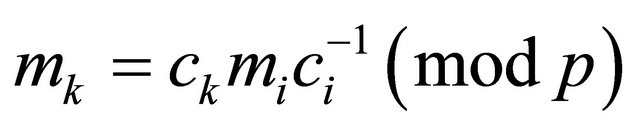 . (4.10)
. (4.10)
Analogously, the encryption (4.3) is vulnerable for cryptanalysis if at least one plaintext block, 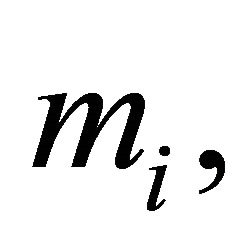 becomes known, the intruder can compute every plaintext
becomes known, the intruder can compute every plaintext 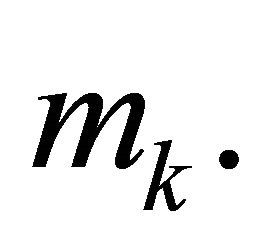 Indeed, since (4.3) implies
Indeed, since (4.3) implies
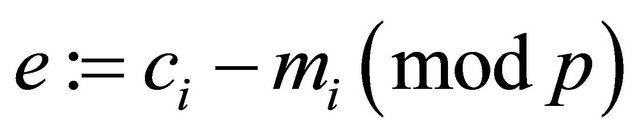 ; (4.11)
; (4.11)
then
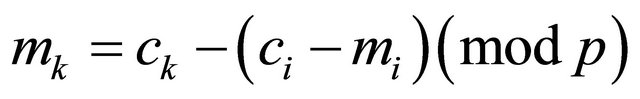 . (4.12)
. (4.12)
In order to overcome these deficiencies, the sender must compute dedicated encryptor e(m) for every plaintext
Table 1. Computation of MMI.

Table 2. Computation of MMI of 195 modulo p‒1=862.
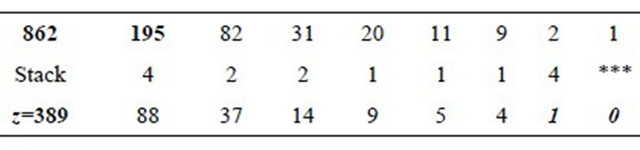
Table 3. Algorithm for MMI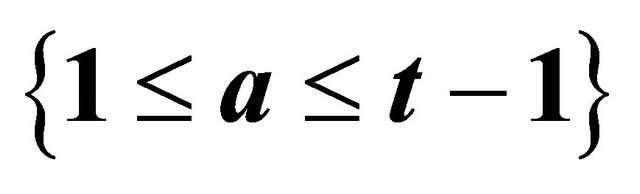 .
.

block m, and respectively, the receiver must compute dedicated decryptor d(m) to recover this plaintext. Needless to say that this requires additional computational efforts, i.e., it slows the transmission of information.
5. Dynamic Establishment of Secret Key between Sender and Receiver
Step5.1: The sender (Alice) selects a large safe prime p and transmits it to the receiver (Bob) via an open channel;
Step5.2: Respectively, Alice and Bob randomly select large integers a and b as their private keys;
Step5.3: Alice and Bob independently compute their public keys:
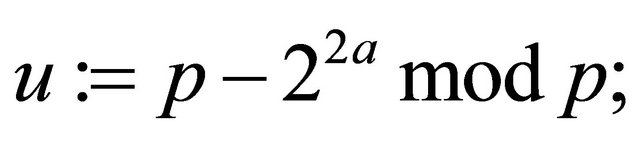 (5.1)
(5.1)
and
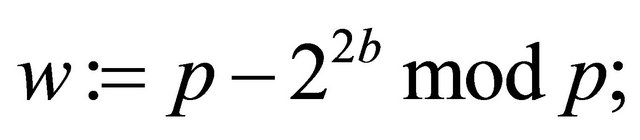 (5.2)
(5.2)
Step5.4: The sender (Alice) selects an ephemeral secret key x, and using the public key of the receiver, she computes an ephemeral encryptor
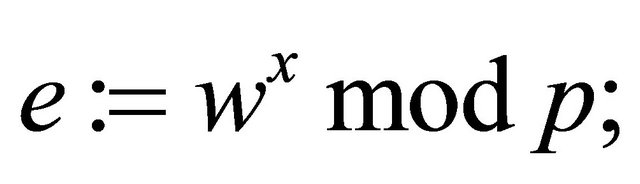 (5.3)
(5.3)
and her hint
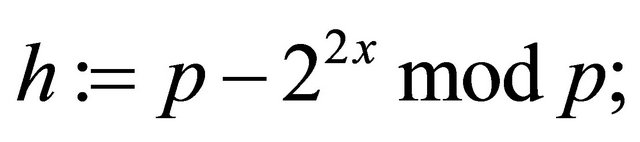 (5.4)
(5.4)
Remark5.1: Parameters a, b, e and x must be distinct from 1, q and p−1.
Step5.5: The sender computes the ciphertext
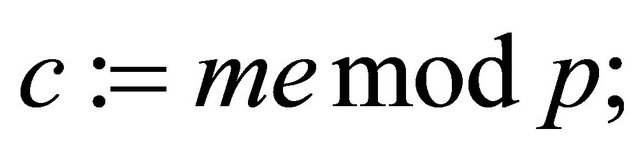 (4.2);
(4.2);
and transmits {c,h} to the receiver;
Step5.6: Using his public key, the receiver computes an ephemeral decryptor
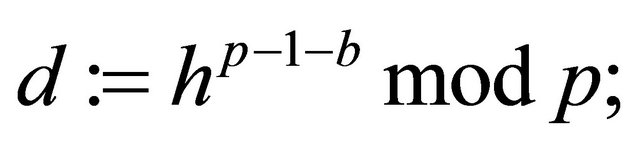 (5.5)
(5.5)
and then computes
 (4.6);
(4.6);
Remark5.2: As an alternative, the sender computes the ciphertext
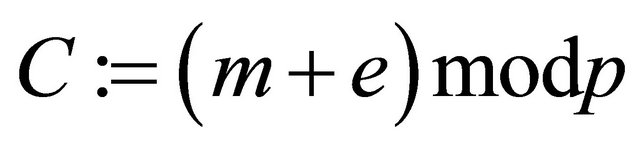 (4.3);
(4.3);
and sends (C,h) to the receiver.
In this case, the receiver computes his ephemeral decryptor 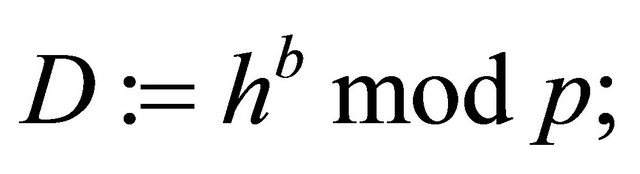 (4.7) and then computes
(4.7) and then computes  (4.8), i.e., he recovers the original plaintext.
(4.8), i.e., he recovers the original plaintext.
6. Numeric Illustrations-1
In the Examples 1 and 2 modifications that simplify the computation are introduced, and as a result, accelerate the secure transmission of information.
First of all, notice that there is no necessity to search for a generator in order to compute the hints and public keys.
Example1 {Alice sends message m to Bob}:
Let p=47; g=4; b=25; x=33; and m=42.
Encryption:
Step6.1.1: Bob pre-computes his public key
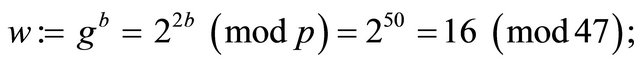
Step6.2.1: Alice computes her hint
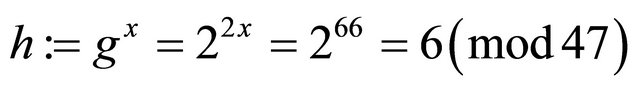
Step6.3.1: Using Bob’s public key w, Alice computes her encryptor e and the ciphertext C:
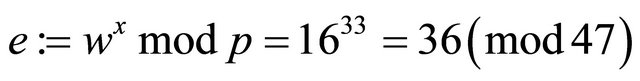 ;
;
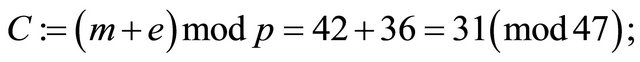
Step6.4.1: Alice sends the ciphertext and her hint to Bob: 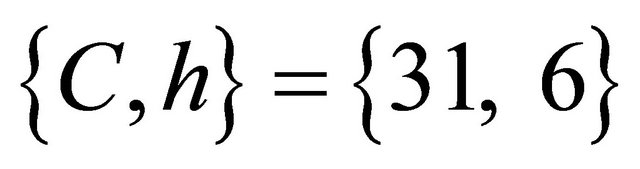 ;
;
Decryption:
Step6.5.1: Using his private key b, Bob computes his decryptor
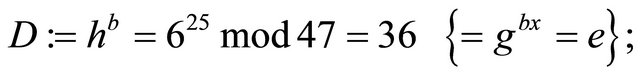
Step6.6.1: Bob decrypts the ciphertext:
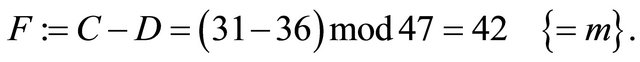
i.e., he recovers the plaintext m.
Example2: Let now p=863; g=4; a=35; y=21; m=754; and suppose Bob wants to send a secret message m to Alice.
wang#title3_4:spEncryption:
Step6.1.2: Alice pre-computes her public key
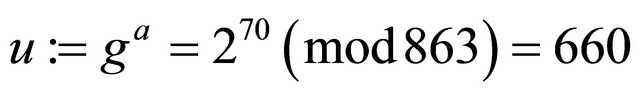 ;
;
Step6.2.2: Bob computes his hint
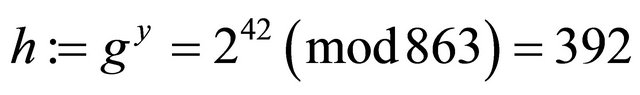 ;
;
Step6.3.2: Bob computes the ephemeral secret encryptor e and ciphertext C:
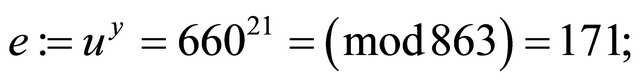
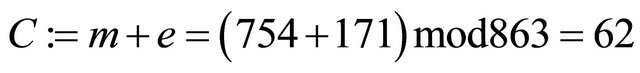 (5.1);
(5.1);
Step6.4.2: Bob sends the ciphertext C and his hint h to Alice.
wang#title3_4:spDecryption:
Step6.5.2: Using her private key a and hint h, Alice computes her ephemeral decryptor D: 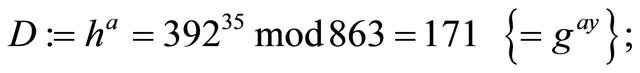
Step6.6.2: Alice decrypts the ciphertext:
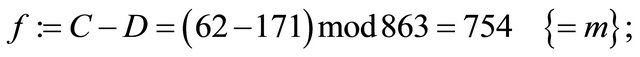
i.e., she recovers the plaintext m.
Remark6.3: If the plaintext is intelligible, Alice accepts it as legitimate, i.e. this protocol also provides a digital signature.
7. Encryption via Exponentiation with Secret Encryptor (EvESE)
The following encryption/decryption scheme requires fewer exponentiations than the schemes described above.
System design:
a). Users Alice and Bob select their private keys a and b respectively and then compute their public keys:
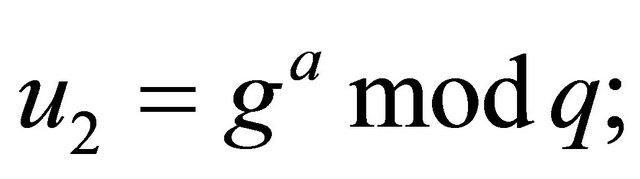 (7.1)
(7.1)
and
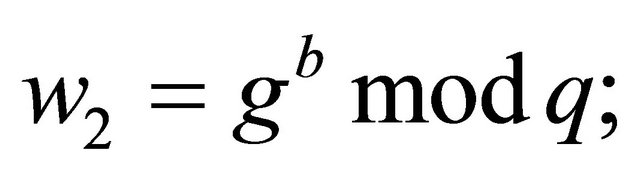 (7.2)
(7.2)
b). each user computes his/her common secret encryptor
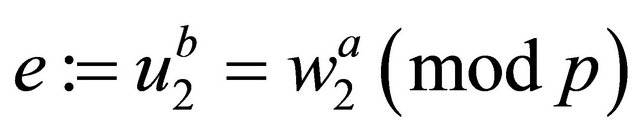 ; (7.3)
; (7.3)
c). if e and p−1 are relatively primei.e., if
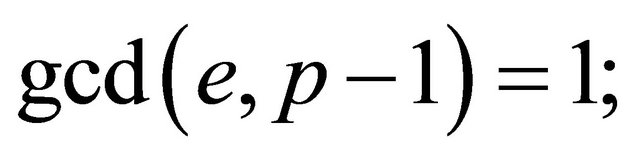 (7.4)
(7.4)
then the users compute an integer d that satisfies the equation
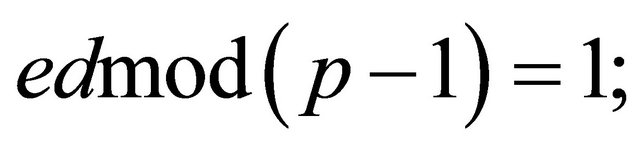 (7.5)
(7.5)
else, {if 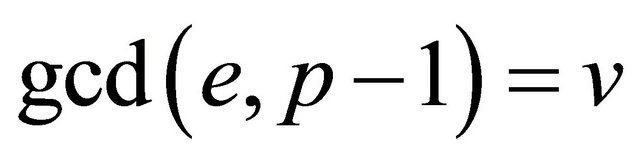 }they consider
}they consider
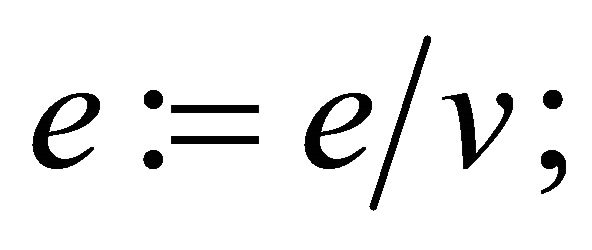 (7.6)
(7.6)
and compute d in (7.5). To find d (decryptor), both users compute
 (7.7)
(7.7)
Remark7.1: As an alternative the users can apply the algorithm for MMI, [10,11]; {see Examples 3, 4 and Table 3};
wang#title3_4:spEncryption:
d). A sender of message m computes the ciphertext
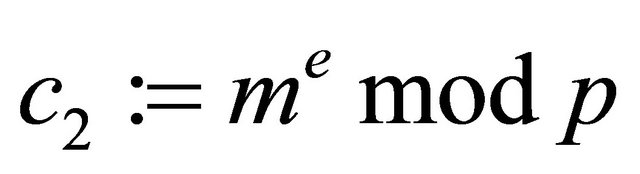 ; (7.8)
; (7.8)
e). the ciphertext 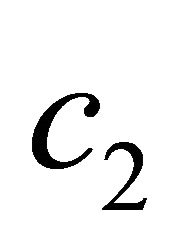 is sent to a receiver via an open communication channel{notice that no any hint is necessary!};
is sent to a receiver via an open communication channel{notice that no any hint is necessary!};
wang#title3_4:spDecryption:
f). The receiver computes
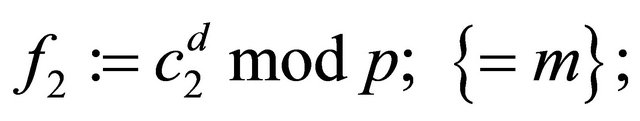 (7.9)
(7.9)
Validation of EvESE Algorithm:
Since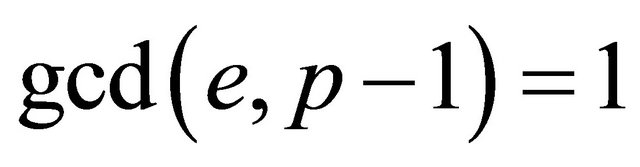 , i.e., e is odd and distinct from q, then (7.5) implies the existence of an integer k such that
, i.e., e is odd and distinct from q, then (7.5) implies the existence of an integer k such that
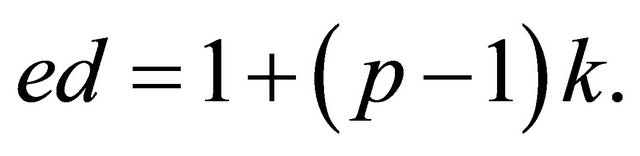 (7.10)
(7.10)
Therefore, (7.8) and the FLT imply that
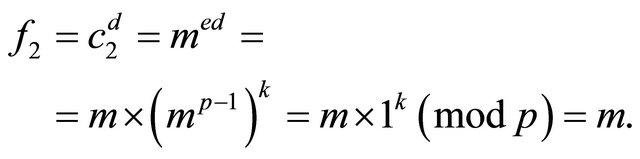 (7.11)
(7.11)
Remark7.2: Although (7.8) and (7.9) resemble the RSA protocol [4], there are three distinct features:
1). the encryptor e is a secret (not public!) key;
2). modulo reduction is executed with the public prime p rather than with the product of two secret primes individually selected for each user;
3). this scheme does not require additional computations for sender identification; in other words, it automatically provides the digital signature.
8. Numeric Illustrations-2
Example3: Let p=107; g=4; a=33; b=28; and m=42.
System design: {either a or b must be selected in such a way that 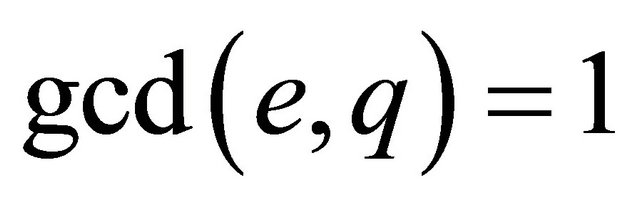 otherwise the MMI of e modulo q does not exist};
otherwise the MMI of e modulo q does not exist};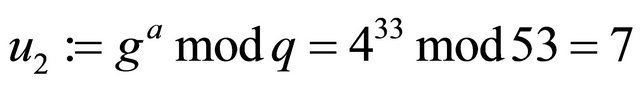 ;
;
and
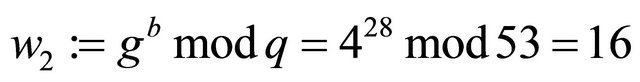 ;
;
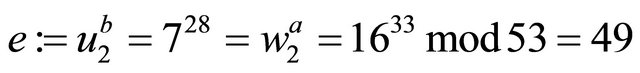 ;
;
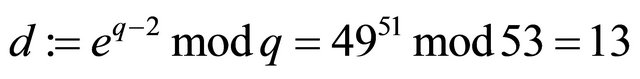 . (8.1)
. (8.1)
Remark8.1: If q is a very large integer, the computation of the multiplicative inverse in (8.1) requires many multiplications even if the “square-and-multiply” algorithm is used. Yet, computation of the MMI is much simpler using the algorithm described in [10] as it is shown in the Table 1:
Since the number of columns in the Table 1 is even, then d:=z.
Verification: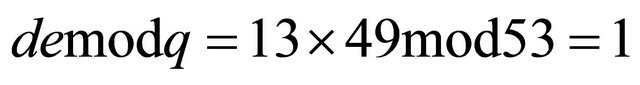 .
.
Explanations are provided in Section 9.
Encryption: A sender computes the ciphertext 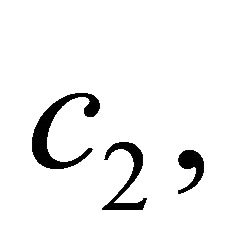 and transmits it to the receiver:
and transmits it to the receiver:
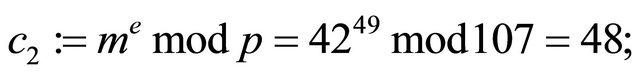
Decryption: {using the decryptor d, the receiver recovers the plaintext}:
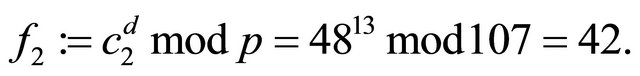 Therefore, the message m is correctly recovered by the receiver.
Therefore, the message m is correctly recovered by the receiver.
Example4: Let now p=863; g=4; a=35; b=49; and m=756.
System design:
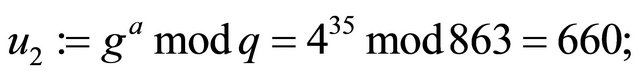
and
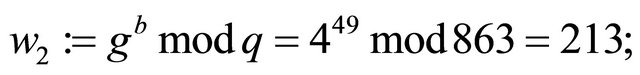
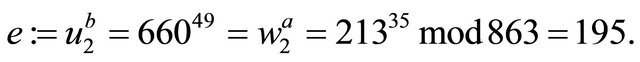
Each user computes the MMI of 195 modulo 862; details are shown in the Table 2:
Since the number of columns in the Table 2 is odd, then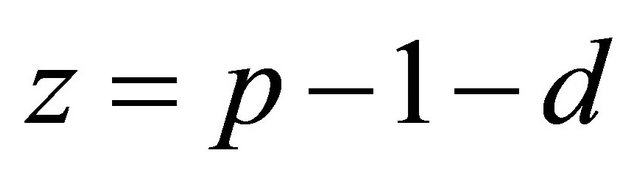 ; therefore
; therefore
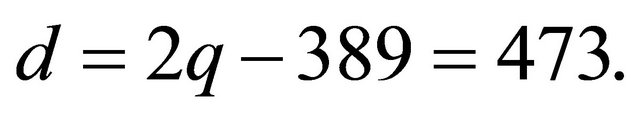
Encryption:
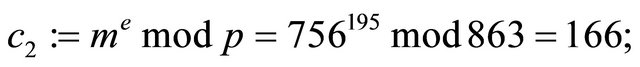
Decryption:
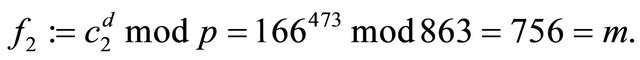
9. Algorithm for MMIazmodt=1
In this section, Table 3 briefly describes the algorithm for the MMI. For more details, see [10] and [11].
In the following Table 3 both integers a and t are the inputs and integer z is the output.
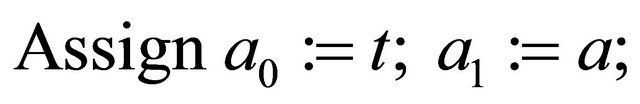
for 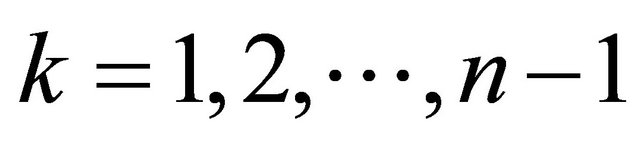 iterate and store in a stack the quotients
iterate and store in a stack the quotients
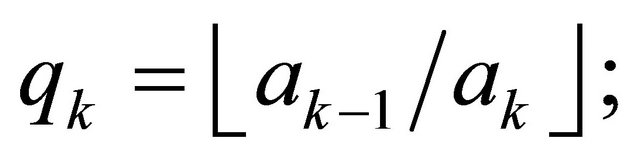
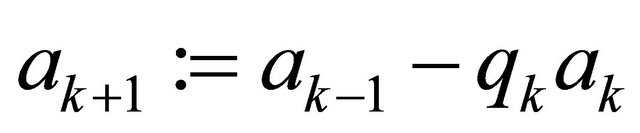 ;
;
repeat until 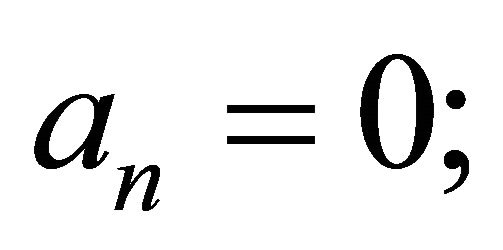 or
or 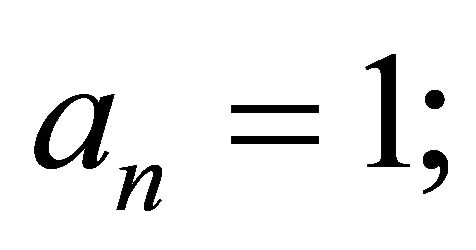
if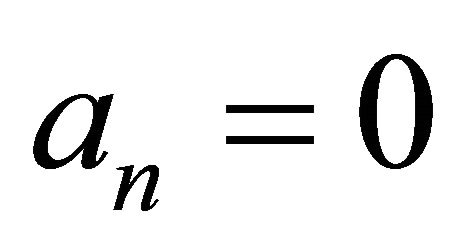 , then the MMI does not exist;
, then the MMI does not exist;
if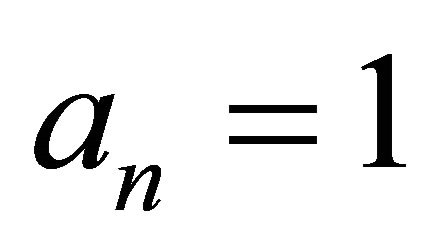 , then assign
, then assign ; and
; and 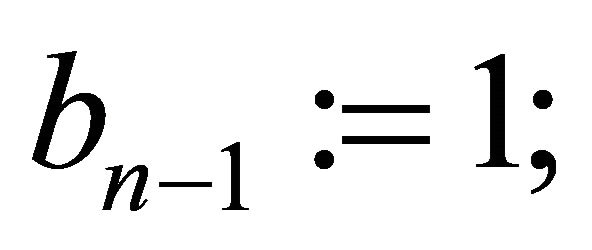 for k from n−1 down to 1 iterate
for k from n−1 down to 1 iterate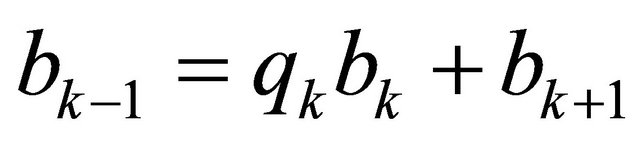 ;
;
if n is odd, then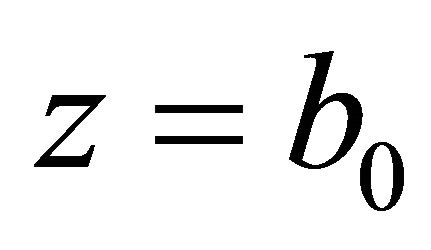 , else
, else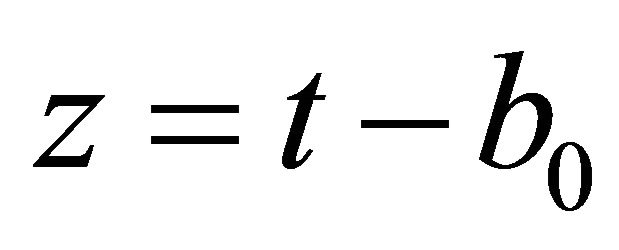 .
.
10. Complexity Analysis of EvESE Cryptosystem
On the system design level, each user performs two exponentiations to compute their public key (7.1) and (7.2), and the secret encryptor (7.3).
For the encryption, it is necessary to perform only one exponentiation (7.5). Analogously, for decryption, every receiver performs only one exponentiation (7.7). Although for the purpose of maintaining a high security level we need periodically select new private keys and re-compute the encryptor and decryptor, we do not need to send the hints with every block of transmitted message like it is done in the ElGamal algorithm. Since this algorithm is based on the difficulty of the DLP, it has certain advantages over the RSA algorithm based on factorization. One of them is that the encryptor and decryptor provide a digital signature (sender identification) since they are computed for communication between the specific pair of users (Alice and Bob). On the other hand, in the described form the algorithm cannot be applied for broadcasting of secret messages to several users. However, using the “carrousel” DHKE, we can generalize the proposed algorithm for communication among several users.
11. Algorithm EvESE Modification
If e is a power of 2, or 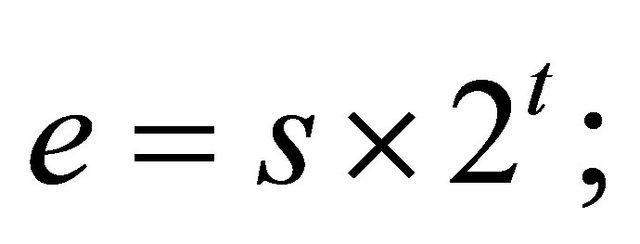 where
where 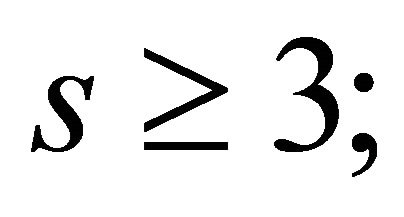 and s is a small integer, then the algorithm does not work, since the decryptor either does not exist or the encryptor is too small. One option is to select new private keys a and b in hope that new e will be more suitable. However, this is a non-deterministic procedure. Besides it requires many multiplications of multidigit-long integers.
and s is a small integer, then the algorithm does not work, since the decryptor either does not exist or the encryptor is too small. One option is to select new private keys a and b in hope that new e will be more suitable. However, this is a non-deterministic procedure. Besides it requires many multiplications of multidigit-long integers.
There are other simple options if p>11, e is even and 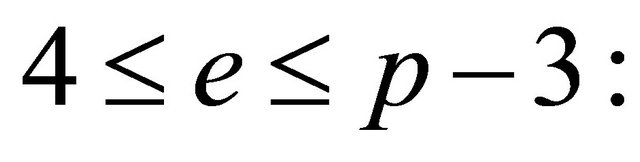
a). if 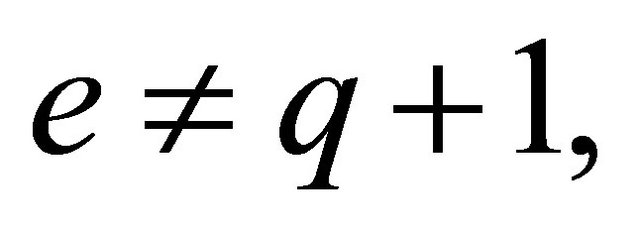 then assign
then assign 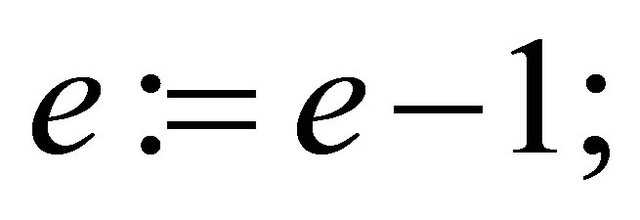
b). if 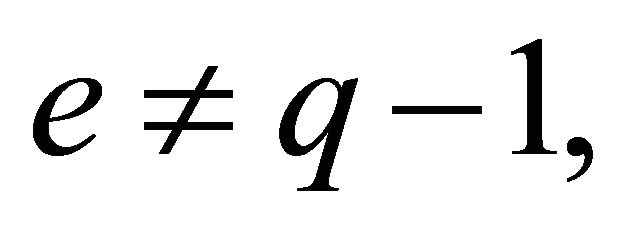 then assign
then assign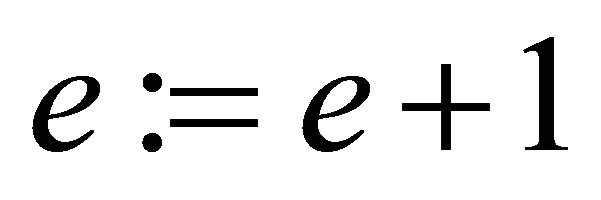 .
.
Finally, if e=2, then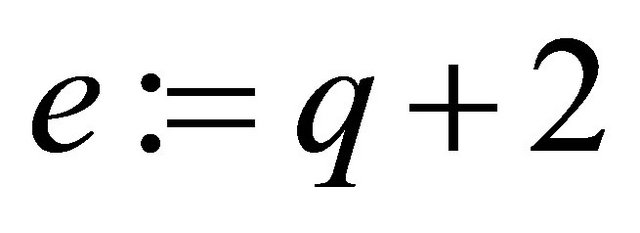 .
.
12. Conclusions
Notice that the ElGamal algorithm is just one of several constructive demonstrations how to dynamically apply a secret key for secure communication. Indeed, the inverse value of the decryptor is the same as encryptor. Therefore, both parties are dynamically establishing the common secret key (encryptor e) and then use it to hide the message m by multiplying it on the encryptor. Another possibility: instead of multiplying, they add the encryptor e to m or can consider exponentiation  Therefore, in the case of addition in (4.3), they eliminate two multiplications for every plaintext since D=e.
Therefore, in the case of addition in (4.3), they eliminate two multiplications for every plaintext since D=e.
However, both protocols require twice more exponentiations than the EvESE algorithm described in the Section 7 and demonstrated in Section 8. As the analysis shows, the most efficient is to use the exponentiation (7.5) for the encryption.
I wish to express my appreciation to Dr. Roberto Rubino for his comments that improved the style of this paper.
REFERENCES
- W. Diffie and M. E. Hellman, “New Directions in Cryptography”, IEEE Transactions on Information Theory, Vol. 22, No. 6, 1976, pp. 644-654. doi:10.1109/TIT.1976.1055638
- A. J. Menezes, P. C. van Oorschot and S. A. Vanstone, “Handbook of Applied Cryptography”, CRC Press, Boca Raton, 1997.
- T. ElGamal, “A Public Key Crypto-System and a Signature Scheme Based on Discrete Logarithms”, IEEE Transactions on Information Theory, Vol. 31, No. 4, 1985, pp. 469-472. doi:10.1109/TIT.1985.1057074
- R. L. Rivest, A. Shamir and L. M. Adleman, “A Method of Obtaining Digital Signature and Public-Key Cryptosystems”, Communication of ACM, Vol. 21, No. 2, 1978, pp. 120-126. doi:10.1145/359340.359342
- C. F. Gauss, “Disquisitiones Arithme Ticae”, 2nd Edition, Springer, New York, 1986.
- P. Garrett, “Making, Braking Codes: An Introduction to Cryptology”, Prentice Hall, Upper Saddle River, 2001.
- B. Verkhovsky, “Deterministic Algorithm Computing All Generators: Application in Cryptographic Systems Design”, International Journal of Communications, Network and System Sciences, Vol. 5, No. 11, 2012, pp. 715-719. doi:10.4236/ijcns.2012.511074
- J. Katz and Y. Lindell, “Introduction to Modern Cryptography”, Chapman and Hall/CRC Press, New York, 2008.
- B. A. Forouzan, “Cryptography and Network Security”, McGraw Hill, Boston, 2008.
- B. Verkhovsky, “Multiplicative Inverse Algorithm and Its Space Complexity”, Annals of European Academy of Sciences, EAS, Liege, 2004, pp. 110-124.
- B. Verkhovsky, “Space Complexity of Algorithm for Modular Multiplicative Inverse”, International Journal of Communications, Network and System Sciences, Vol. 4, No. 6, 2011, pp. 357-363. doi:10.4236/ijcns.2011.46041

