Technology and Investment
Vol. 3 No. 4 (2012) , Article ID: 24769 , 7 pages DOI:10.4236/ti.2012.34029
Equity Market or Bond Market—Which Matters the Most for Investment? Revisiting Tobin’s q Theory of Investment
Department of Economics, New School for Social Research, New School University, New York, USA
Email: semmlerw@newschool.edu, matel236@newschool.edu
Received August 2, 2012; revised September 2, 2012; accepted September 10, 2012
Keywords: Equity Market; Bond Market; Tobin’s q Theory of Investment
ABSTRACT
Recent experience seems to have shown that credit markets are more important than equity markets for investment and macrodynamics. This paper examines the effect of Tobin’s equity q and bond q on investment. More specifically we study the role of Tobin’s equity (usual) q, average q and bond q for aggregate investment over the period 1953: Q4-2011: Q1. Employing bond q and equity q, or alternatively bond q and average q, shows that these variables are very relevant in explaining investment. Yet, the time scale matters too. Examining the relationship of these variables over a long time scale, at low frequencies, we can show that the combination of bond q and average q are the most significant determinants of aggregate investment. Moreover, for the longer time scale the two variables, bond q and average q, result in the highest goodness of fit demonstrating good in-sample forecasting properties. As to the individual determinants of aggregate investment over the period 1953: Q4-2011: Q1, bond q is by far the most influential variable at all frequencies since it always has the highest correlation with investment and this correlation is always statistically significant. Similarly, the greater significance of average q, as compared to equity q, is probably an outcome of the financing instruments for investment.
1. Introduction
In macroeconomics one of the most contentious issue is the theory and empirics of investment. Tobin’s seminal work that investment is guided by the value of the asset of the firm in the stock market has become the standard theory of investment. It is based on some measure of the stock market value of the firm (value of corporate equity) relative to the replacement cost of its existing capital. This measure is denoted as Tobin’s q in the literature, and as a result Tobin’s q is used as a main determinant of a firms’ investment decision. Numerous theoretical and empirical studies on this issue have been conducted, but as has also been noted, for example by [1,2], the relation between Tobin’s q and investment has been quite an empirical failure. Amongst other reasons, this may reflect that the market valuation of a firm’s assets is very volatile and there seem to be other relevant factors determining investment.
Numerous articles have been published that showed, those factors such as expectations, the distinction between investment decisions and investment spending1, credit and financing constraints are important as well. In a simplistic view, to finance an investment project a firm could consider the following: 1) Using retained profits (internal finance); 2) Issuing a debt instrument for example a bond (external finance); 3) Selling equity or shares (external finance) and 4) Obtaining loans from a bank or financial institution (external finance).
Although a firm may have financing opportunities and even if it faces no financing constraint, there are still more factors that may be taken in to consideration before undertaking an investment project. Moreover, the decision on the type of external financing is a factor. A firm may aim at obtaining or issuing a debt instrument. By issuing a debt instrument, this allows a firm to fully benefit from the net profits or tax advantages. On the other hand, a firm may intend to issue shares (equity). Issuing shares has the downside of paying out profits, but it has the upside of spreading the risk in the event that a project is not profitable. Recently the major issue has become to what extent firms’ investments are determined by the value of equity or by conditions of the credit markets (bond issuing and loans from banks). One can state those alternative investment rules by saying: What drives investment? Is it Tobin’s equity q or Tobin’s bond q? In addition, we would want to explore which determinants are relevant on different time scales.
The traditional theory of investment provides an elegant representation of a firms’ decision problem, relating investment to the value of the equity of a firm. In addition, the theory yields a simple investment rule derived from a firms’ decision problem. This paper examines whether the determinants of investment are bond q and equity q. We will also use a less conventional q measure, namely an average q. As a result, we will employ alternatively equity q and average q. Using bond q and equity q or bond q and average q, allows us to take in to account other factors beyond stock market valuation as being the key factor determining investment. As to the time scale of the link between the different q’s and investment we examine the relation between investment, bond q and equity q and the relation between investment, bond q and average q, whereby all the variables are evaluated at higher and lower frequencies.
The remainder of the paper is organized as follows: Section 2 presents an outline of the standard theory of investment. Section 3 discusses the methodology and data sources. Section 4 presents the estimation results and Section 5 concludes the paper.
2. The Standard Theory of Investment Model
In this section, we present a modified neoclassical investment model that characterizes the representative firm’s decision problem and we use this to derive the relation between investment and Tobin’s q. The modification we introduce is in the form of adjustment costs and based on the derivation, we express a regression equation that we estimate. We follow a similar framework to that outlined by [3]. In addition, we employ Pontryagin’s maximum principle and also evaluate the local stability properties around the steady state of each variable of interest.
The objective of the representative firm is to determine investment that maximizes the present value of its net profit over an infinite horizon, and this is presented as follows:
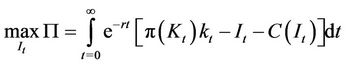 (1)
(1)
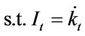 (2)
(2)
where 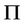 is the present value of the firms’ net profit over an infinite horizon,
is the present value of the firms’ net profit over an infinite horizon, 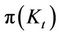 is the real flow of profits for the firm per unit of capital, and kt is the firm’s capital stock. In line with [3], we assume the discount rate r is constant and that Kt the industry wide capital stock trajectory is taken as given by each firm and each firm chooses its investment over time to maximize
is the real flow of profits for the firm per unit of capital, and kt is the firm’s capital stock. In line with [3], we assume the discount rate r is constant and that Kt the industry wide capital stock trajectory is taken as given by each firm and each firm chooses its investment over time to maximize 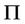 for a given Kt. The real flow of profits for the firm,
for a given Kt. The real flow of profits for the firm, 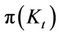 , are inversely related to Kt. We also assume that there is a zero depreciation rate and in line with [4] we also assume that the purchase price of a unit of investment good is one and hence the cost of purchasing an investment good is It.
, are inversely related to Kt. We also assume that there is a zero depreciation rate and in line with [4] we also assume that the purchase price of a unit of investment good is one and hence the cost of purchasing an investment good is It.
In other studies such as [5], the adjustment costs of investing are a convex function of the investment rate. In line with [4], we assume that adjustment costs are a convex function of the level of investment and are given as  ,
, 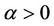 , where
, where  (for all
(for all 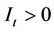 ) and
) and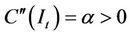 .
.
To solve the problem that the representative firm faces we employ Pontryagin’s maximum principle and formulate the current value Hamiltonian. The current value Hamiltonian is expressed as follows:
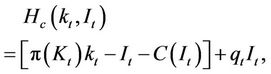 (3)
(3)
where 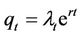 and qt denotes the market value of a unit of capital. Substituting the explicit adjustment costs function in the current value Hamiltonian results in the following:
and qt denotes the market value of a unit of capital. Substituting the explicit adjustment costs function in the current value Hamiltonian results in the following:
 (4)
(4)
The first order conditions derived from (4) are as follows:
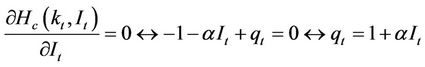
also expressed as:
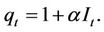 (5)
(5)
The law of motion for the co-state variable is:
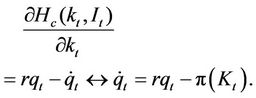 (6)
(6)
The transversality condition can be written as follows:
 .
.
Equation (5) implies an investment rule which is that firms invest until the total cost of an additional unit of capital is equal to the market value of a unit of capital. Equation (5) can also be interpreted as the market value of a unit of capital is also equal to the marginal value of an additional unit of capital. We show this alternative interpretation in the Appendix (A1) by using the Hamilton-Jacobi-Bellman method to solve the firm’s maximization problem and this yields the same result as shown in Equation (5). Although Equation (6) is the law of motion for the co-state variable, it also implies that the marginal revenue of capital is equal to its opportunity cost2.
Using Equation (5) allows us to determine the optimal investment level that maximizes the current value Hamiltonian and this is represented as follows:
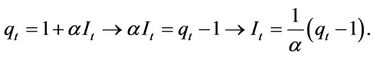 (7)
(7)
Using Equation (5) we can now reach the following optimal investment rules:
1) When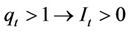 , 2) when
, 2) when  and 3) when
and 3) when . In the literature, the standard measure of Tobin’s q is the ratio of a firm’s stock market valuation relative to the replacement cost of its physical asset. Using this approach, if qt is greater than one, then a firm should undertake an investment project because the market values the firm’s assets beyond the cost associated with taking on an investment project. Even with the implied investment rule based on the derivation of Equation (5), [2,6] note that the critical variable which is marginal q and in this context as derived in Equation (5) is unobservable. As a result, empirical work based on the q theory of investment is based on its average measure, where the average measure is used as a proxy for marginal q. Moreover, [2] note that the average measure as a proxy is used with stock market valuations only under stringent conditions which are linear homogeneity of the profit and adjustment cost function.
. In the literature, the standard measure of Tobin’s q is the ratio of a firm’s stock market valuation relative to the replacement cost of its physical asset. Using this approach, if qt is greater than one, then a firm should undertake an investment project because the market values the firm’s assets beyond the cost associated with taking on an investment project. Even with the implied investment rule based on the derivation of Equation (5), [2,6] note that the critical variable which is marginal q and in this context as derived in Equation (5) is unobservable. As a result, empirical work based on the q theory of investment is based on its average measure, where the average measure is used as a proxy for marginal q. Moreover, [2] note that the average measure as a proxy is used with stock market valuations only under stringent conditions which are linear homogeneity of the profit and adjustment cost function.
Nevertheless, the standard investment model assumes that all firms in an industry are identical. As a result, if there are N firms in the industry, it follows that economy wide capital accumulation is expressed as follows:
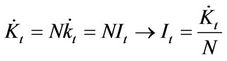 . (8)
. (8)
From Equation (5) we have that  and
and  which is then expressed as
which is then expressed as
 but from (8),
but from (8), 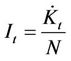 and hence we have the following:
and hence we have the following:
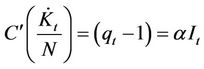 , (9)
, (9)
which is a monotonic function, is a one-to-one function and is an onto function. As a result, and as noted by [7] the inverse exists, that is 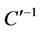 exists which then allows us to have
exists which then allows us to have . Defining the inverse in a general functional form results in the following:
. Defining the inverse in a general functional form results in the following:
 , (10)
, (10)
and from this we obtain the following:
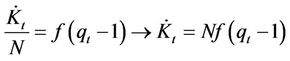 . (11)
. (11)
Equation (11) allows us to observe the relation between economy wide capital accumulation and Tobin’s q. The function 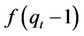 is a monotonic function and it preserves the properties of the original function
is a monotonic function and it preserves the properties of the original function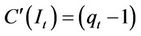 . As a result, we have the following:
. As a result, we have the following:
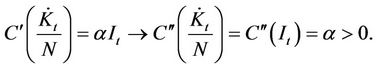 (12)
(12)
Similarly because 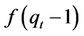 preserves the properties of the original function, we then have the following:
preserves the properties of the original function, we then have the following:
 , (13)
, (13)
 (14)
(14)
Using Equations (6) and (11) we then have a system of two differential equations which are derived from the firms optimizing strategy. The system of two differential equations is as follows:
 , (15)
, (15)
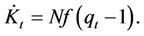 (16)
(16)
We now proceed to determine the steady state values of the system and then analyze local stability around the steady. The steady state is determined as follows:
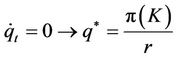 (17)
(17)
and using Equations (8) and (16) we then have that when
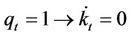 , and
, and  and
and .
.
The differential equations are non-linear because we do not have the explicit form of the function , and also do not have the explicit form of the function
, and also do not have the explicit form of the function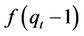 . As a result, we linearize the system of differential equations. The linearized forms of Equations (15) and (16) are expressed as follows:
. As a result, we linearize the system of differential equations. The linearized forms of Equations (15) and (16) are expressed as follows:
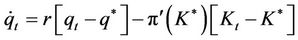 , (18)
, (18)
 , (19)
, (19)
which in matrix form can be expressed as follows:
 (20)
(20)
The Jacobian matrix analyzed at the steady state is as follows:
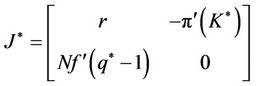 .
.
The trace of the Jacobian matrix at steady state is Trace  and the determinant of the Jacobian matrix at steady state is Determinant
and the determinant of the Jacobian matrix at steady state is Determinant
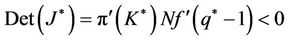 where
where 
and . As a result, the system exhibits saddle path stability.
. As a result, the system exhibits saddle path stability.
3. Methodology and Data
In this section we present the methodology we use to estimate the relation between investment, Tobin’s equity q and bond q. In addition, we explain the data that we use in our analysis. The analysis in the paper is for the U.S. economy. We estimate an equation using a particular representation and transformation of the first order condition expressed in Equation (7). We estimate an equation between the investment rate, Tobin’s q and bond q and we use two forms of observable Tobin’s q, namely equity (usual) q and also average q. In line with [1,2], we estimate the following equations using OLS with NeweyWest HAC consistent standard errors. The equations are as follows:
 , (21)
, (21)
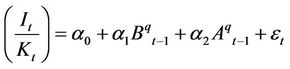 . (22)
. (22)
The transformation in relation to (7) is consistent with empirical estimations and as a result we use the investment rate denoted as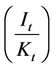 , as a dependent variable and not the level of investment. For our empirical analysis, Tobin’s equity q is denoted as
, as a dependent variable and not the level of investment. For our empirical analysis, Tobin’s equity q is denoted as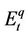 , and is defined as the ratio of the market value of corporate equity to net worth (total assets minus total liabilities). Average q, is denoted as
, and is defined as the ratio of the market value of corporate equity to net worth (total assets minus total liabilities). Average q, is denoted as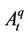 , and is defined as the ratio of the sum of the market value of corporate equity and total liabilities to total assets. The data for constructing average and equity q is derived from the Federal Reserve Board’s Flow of Funds account Z1 statistical release for March 8th, 20123. The values are not seasonally adjusted and are for Nonfinancial Corporate business. Bond q, which is also referred to as the relative price of corporate bonds is computed in line with [1,2] as
, and is defined as the ratio of the sum of the market value of corporate equity and total liabilities to total assets. The data for constructing average and equity q is derived from the Federal Reserve Board’s Flow of Funds account Z1 statistical release for March 8th, 20123. The values are not seasonally adjusted and are for Nonfinancial Corporate business. Bond q, which is also referred to as the relative price of corporate bonds is computed in line with [1,2] as 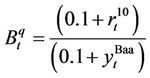 where
where  is the 10 year treasury constant maturity rate and
is the 10 year treasury constant maturity rate and 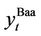 is Moody’s Baa Corporate bond yield. The data for computing bond q is derived from the Board of the Federal Reserve System (FRED)4. For investment and capital stock, we use the series on private non-residential fixed investment in equipment and structures and the corresponding current cost of net capital stock from the Bureau of Economic Analysis5.
is Moody’s Baa Corporate bond yield. The data for computing bond q is derived from the Board of the Federal Reserve System (FRED)4. For investment and capital stock, we use the series on private non-residential fixed investment in equipment and structures and the corresponding current cost of net capital stock from the Bureau of Economic Analysis5.
4. Estimation Results
In this section we present the estimation results of Equations (21) and (22). In addition we present the estimation results of Equations (21) and (22) using the low frequency component of each variable. The low frequency component is the trend component of each variable, which we construct using a HP filter6. We use the trend component of each variable so as to capture the relationship between the variables when they are analyzed at low frequency which should reflect long run trends. Table 1 reports the standard regression results for Equations (21) and (22). The Wald joint coefficient test indicates that jointly, bond q and equity (usual) q have an effect on the investment rate. Similarly, based on the Wald joint coefficient test, both bond q and average q have an effect on the investment rate.
Over the period 1953: Q4-2011: Q1, using either average q or equity q and taking into account serial correlation with a four quarter moving average, the percentage point responsiveness of the investment rate with respect to bond q is approximately the same. In addition, the

Table 1. Standard regression output 1953: Q4-2011: Q1.
goodness of fit is relatively the same where bond q and average q or bond q and equity q explain 63% of the variation in the investment rate. This result of the goodness of fit is fairly similar with [1,2] results over their full sample periods which are 1953: Q3 to 2007: Q2 and 1952: Q1-2009: Q4, respectively.
Another similar result to that of [1,2] is that in both the regressions using either bond q and average q or bond q and equity q, bond q is more correlated with the investment rate as compared to the other regressors. Furthermore bond q is always statistically significant at all levels of significance and the striking similarity is also captured in the regression where bond q and equity q are used, where in this context equity q has no explanatory power.
Table 2 reports the regression results for Equations (21) and (22) conducted with their respective trend variables. The Wald joint coefficient test indicates that jointly, the trend of bond q and trend of equity q have no effect on the investment rate. In addition, the percentage point responsiveness of the investment rate with respect to bond q and the percentage point responsiveness of the investment rate with respect to equity q are individually statistically insignificant when using the trend components of the variables. This result probably shows and captures the low variation in either one of the variables because of the smoothness of the trend.
On the other hand, the Wald joint coefficient test shows that jointly the trend of bond q and the trend of average q have an effect on the trend of the investment rate. In addition, the percentage point responsiveness of the investment rate with respect to bond q and percentage point responsiveness of the investment rate with respect to average q are individually quantitatively and statistically significant when using the trend component of the variables. Furthermore, the percentage point responsiveness of the trend of the investment rate with respect to the trend of bond q and the trend of average q are the highest as compared to any other coefficients and the goodness of fit of 82% is also the highest showing good in sample forecasting properties.
Based on Tables 1 and 2, there is evidence that jointly, bond q and equity q or bond q and average q have an effect on the investment rate. In addition, this is supported by the goodness of fit. Even with these findings, an analysis of the trend component of the respective variables shows that it is average q and bond q, rather than equity q and bond q, which jointly and individually affect the investment rate. This is consistent with the interpretation that over the long term, bond q and average q rather than bond q and equity q determine aggregate investment.
The result that the bond q is so dominant for investment—in the shorter as well longer run may need some qualifications. For example, other liabilities rather than corporate equity also have an important role in the financing of investment projects. Of particular interest, is also that at low frequency bond q and average q reveal the highest goodness of fit and by implication this shows good in-sample forecasting properties.
5. Conclusion
This paper finds evidence that both, bond q and equity q, and alternatively bond q and average q have a strong impact on investment. Yet, an analysis of the time scales of the economic relationships—high and low frequency movements of the data shows that it is average q and bond q, rather than equity q and bond q, that jointly and individually determine the investment rate. Moreover, using the low frequency component of bond q and average q, results in the highest goodness of fit and this implies good in-sample forecasting properties. Based on these findings, using the trend component of the variables, over the long term bond q and average q rather than bond q and equity q determine investment. In some sense, our results replicate earlier studies that equity value
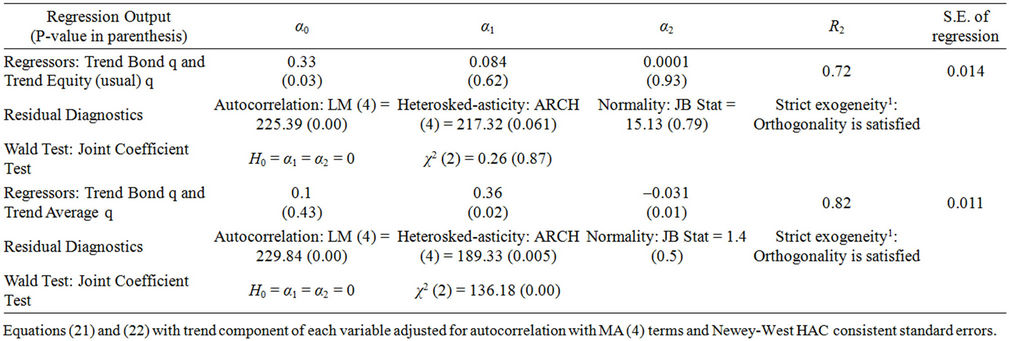
Table 2. Regression with trend component of each variable 1953: Q4-2011: Q1.
appears to be a too noisy variable to conclusively show its impact on investment in the shorter run. If anything it will show up as a relevant factor for investment in the longer run. The credit market and bond market seem to be more important. Thus other liabilities, rather than corporate equity, such as bonds, loans and other debt instruments may be used and may have an important role in the financing of an investment project.
REFERENCES
- T. Philippon, “The Bond Markets q,” Quarterly Journal of Economics, Vol. 124, No. 3, 2009, pp. 1011-1056. doi:10.1162/qjec.2009.124.3.1011
- M. Gallegati, J. Ramsey and W. Semmler, “Bond Prices’ q: With or without Equity Market’s q?” New School University, New York, 2011, pp. 1-25.
- D. Romer, “Advanced Macroeconomics,” 3rd Edition, McGraw-Hill, New York, 2006.
- M. Kato, M. Ofori and W. Semmler, “Tobin’s q and Investment in a Model with Multiple Steady States,” In: T. Asada and T. Ishikawa, Eds., Time and Space in Economics, Springer, Berlin, 2007, pp. 55-80. doi:10.1007/978-4-431-45978-1_4
- L. H. Summers, “Inflation, Taxation and Corporate Investment: A Q Theory Approach,” National Bureau of Economic Research Working Paper, Vol. 600, No. 604, 1980, pp. 61-63.
- F. Hayashi, “Tobin’s Marginal q and Average q: A Neoclassical Interpretation,” Econometrica, Vol. 50, No. 1, 1982, pp. 214-224. doi:10.2307/1912538
- A. C. Chiang and K. Wainwright, “Fundamental Methods of Mathematical Economics,” 4th Edition, McGraw-Hill, New York, 2005.
Appendix A1: Solving the Model Using the Hamilton-Jacobi-Bellman Method
In the outline of the modified neoclassical investment model, Equation (5) implies an investment rule which is that firms invest until the total cost of an additional unit of capital is equal to the market value of a unit of capital. Equation (5) is derived using Pontryagin’s maximum principle. We now use the Hamilton-Jacobi-Bellman method to solve the firm’s maximization problem so that we can show that the market value of a unit of capital is equal to the marginal value of an additional unit of capital.
Using the Hamilton-Jacobi-Bellman method we have the following value function:
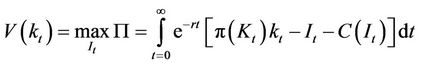 , (A1)
, (A1)
s.t. , and where
, and where .
.
The Hamilton-Jacobi-Bellman equation for (A1) has the following form:
 (A2)
(A2)
Differentiating the Hamilton-Jacobi-Bellman equation with respect to the control variable results in the first order condition which is as follows:
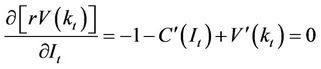 which is also expressed as follows:
which is also expressed as follows:
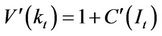 . (A3)
. (A3)
Using the explicit adjustment costs function,
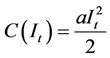 , then
, then 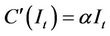 and
and .
.
From the current value Hamiltonian and Equation (5) we have that . This result shows that the market value of a unit of capital, which is qt, is also equal to the marginal value of an additional unit of capital which is
. This result shows that the market value of a unit of capital, which is qt, is also equal to the marginal value of an additional unit of capital which is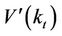 .
.
NOTES
1Differences between investment decisions, investment spending, and the time lag between the two, are discussed in Kaleckian approaches.
2Using a cost function that is quadratic in the investment rate e.g. , yields a non-intuitive and difficult to explain first order condition for the following:
, yields a non-intuitive and difficult to explain first order condition for the following:
![]() . As a result, that is why for the purposes of this paper, we employ a cost function that is quadratic in the level of investment and not quadratic in the investment rate.
. As a result, that is why for the purposes of this paper, we employ a cost function that is quadratic in the level of investment and not quadratic in the investment rate.
3Link to the data is http://www.federalreserve.gov/datadownload.
4To compile bond q, data on Moody’s Baa index is denoted in monthly form. As a result, to be consistent with all other series, we convert the data into quarterly data by using an equally weighted moving average. The link to the data series for bond q is http://research.stlouisfed.org/fred2.
5The current cost of net capital stock is denoted annually and data is in year-end estimates. As a result, we use the year end value of the previous period and divide it by four. We do not use the divided series as a proxy for the quarterly data, instead we take each year end estimate which is divided by four, then compile a quarterly series through linear interpolation between each year end estimate rather than use the whole year end estimate as a proxy for quarter 1 of the following period because this would overstate the value. As a result, each year end estimate is divided by four and is then used as a proxy for the following year quarter one series, then linear interpolation is used through the variables that are proxies so that a series for quarter 2 and quarter 3 can be constructed for each year from 1953: Q1-2011: Q1.
6We use the maximum standard value for  so that we can generate a smooth trend series.
so that we can generate a smooth trend series.

