Technology and Investment
Vol.3 No.1(2012), Article ID:17405,6 pages DOI:10.4236/ti.2012.31001
Inequality and Growth Re-Examined
New School for Social Research, New York, USA
Email: assaj401@newschool.edu
Received November 28, 2011; revised December 28, 2011; accepted January 5, 2012
Keywords: Economic Development; Growth; Income Distribution; Inequality
ABSTRACT
This paper examines the relationship between income inequality and subsequent economic growth. It builds on the model suggested by Alesina and Rodrik (1994) in which inequality works through greater demands for redistribution to slow down growth, and the idea by Ray (1998) that inequality negatively affects savings, work capacity, economic incentives, and access to and efficiency of credit and financial markets. Using an updated dataset and seven model variants, both OLS and 2SLS regressions find a strong negative effect of income inequality on future growth. The effect is considerably stronger for developing countries, but the existence or absence of democracy has no effect on either the relationship between inequality and growth or on the rate of growth itself. There is also no support for Barro’s (2008) claim that inequality impacts growth positively in developed countries.
1. Introduction
Inequality may be objectionable on intrinsic, moral grounds, as well as for functional reasons. The latter are based on the idea that inequality has an instrumental role vis-à-vis other economic processes, such as growth and development. While this is true for countries at any stage of development, Ray (1998) suggests that the consequences “are far more acute for developing countries than for their economically developed counterparts” [1]. Barro (2000) finds that inequality indeed has a negative impact on growth in poor countries, but a positive effect on growth in rich countries [2]. Furthermore, the causality between inequality and growth runs in both directions. For example, Kuznets’s inverted-U hypothesis posits that inequality first rises and then drops as an economy grows. This paper will focus on impacts in the other direction —the effects of initial inequality on subsequent growth.
Recent research confirms the overall negative effects of inequality on growth. Fosu (2009) finds that initial inequality negatively affects the impact of GDP growth on poverty reduction for countries in sub-Saharan Africa [3]. Qin et al. (2009) shows the negative consequences of inequality in China on GDP and sectoral growth [4]. Castelló-Climent (2010) also finds a negative effect of inequality (both income and human capital) on economic growth but only for low and middle-income economies [5].
The theoretical motivation for this study follows the analysis in Alesina and Rodrik (1994, AR below). AR explains the effects of greater inequality (of income, education and land ownership) working through increased demands for redistribution and higher taxes, resulting in lower growth rates. Other channels mentioned by Ray include the negative effects of inequality on savings, work capacity, economic incentives, and access to and efficiency of credit and financial markets [6]. Barro (2000) confirms the role of political economy, credit market imperfections and saving rates, and adds social unrest to this list [7]. In addition to these direct effects, De Gregorio and Lee (2004, quoted in Barro 2008) point out indirect effects of higher inequality: raising fertility, lowering secondary school enrolment and weakening the rule of law [7].
AR discusses heterogeneity in factor ownership (e.g. land ownership, or income and education as proxies) as the cause of differential individual preferences for redistributive policies. Such different preferences would result in a policy compromise (based on the median-voter theory), and the accompanying growth rate may not be the maximum growth rate. The authors clearly find that “the more unequal is the distribution of income and wealth, the lower is the rate of growth” [6]. This is because there would be more pressure for (distortionary) redistributive policies in more unequal societies, reducing the longterm growth rate. However, AR finds no effective difference in growth rates between democracies and non-democracies (since even dictatorships are subject to some pressure). This paper will attempt to study the overall relationship between inequality and growth, regardless of channel, using an updated dataset.
The next section presents the basic model used in this paper and several variants. Section 3 describes the data set, which is then used to estimate the model in Section 4. Section 5 concludes.
2. The Model
Following AR, this paper will examine the impact of initial income inequality within different countries on their subsequent growth rates. The basic model is:
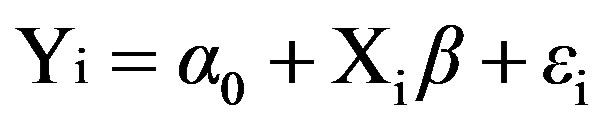 (1)
(1)
where the dependent variable, Yi, is the compound annual growth rate (CAGR). It is calculated for the period 1998-2008 for each country in the sample. The calculation is based on the geometric mean of per capita GDP (in constant 2005 PPP) for the first and last years:
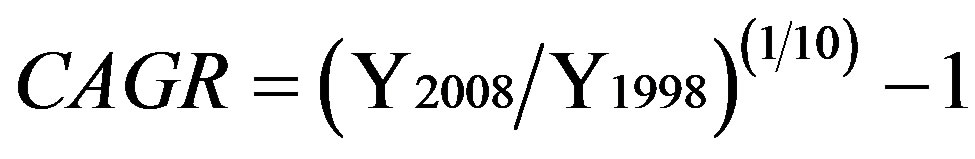
The independent variables matrix, Xi, includes GINI data around 1998 (see Section 3 below), per capita GDP in 1998 (in constant 2005 PPP) and the 1998/99 primary enrolment ratio.
Including a dummy variable for developing countries is useful in examining Ray’s claim that inequality affects developing countries more intensely than developed ones:
 (2)
(2)
where Devi takes a value of 0 for developed countries (high-income economies in the World Bank classification, see Section 3 below), and 1 for developing countries (all other economies).
Furthermore, following Barro (2008), the model for the longer sample (using 2SLS) will include an interaction term between the log of per capita GDP in 1998 and the GINI coefficient, to examine Barro’s finding that inequality has a negative effect for poor countries but a positive one for rich countries [7]. This will be further tested by running separate regressions for developed and developing countries.
An extended model includes a democracy dummy based on the EIU democracy index, in order to check whether the type of regime has an effect on the relationship between inequality and growth (posited by AR to work through pressure for redistribution):
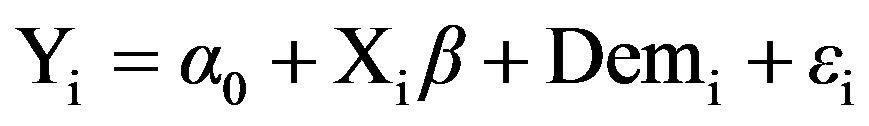 (3)
(3)
where Demi is the democracy dummy, taking a value of 1 for full or flawed democracies and 0 for non-democratic regimes (hybrid and authoritarian). In addition, the model will be estimated with both the development and democracy dummies.
3. The Data
Given the scarcity of data on land inequality, GINI coefficients for income have been used instead (data was available from the World Bank for 141 countries around the year 1998). Following AR, and “to avoid reverse causation from growth to distribution” [6], the sample is first limited to countries with GINI data around the beginning of the period over which growth is measured. However, only 100 of the 141 countries in the full sample have GINI coefficients between 1992 and 1998, preceding the period of growth we seek to explain. For these 100 countries, OLS has been used. In order to include the other countries (with GINI data between 1999 and 2005), Two-Stage Least-Squares estimation is then used to account for the possible endogeneity from growth to inequality during the same period. Appendix I provides a list of all 141 countries in the larger sample and their corresponding dates for income GINI coefficients.
The dependent variable is the compound average growth rate of GDP per capita between 1998-2008 (data for 2009 has been excluded to avoid the effects of the financial crisis), and will be regressed on GINI around 1998, GDP per capita in 1998 and primary education enrolment in the school year 1998/99. As suggested in AR, including initial income per capita accounts for the possibility of convergence, while including initial primary enrollment measures human capital levels.
In addition, two dummy variables—for stage of developpment and type of regime—will be used. The World Bank income classification (as of January 2011) used in the analysis is as follows (based on annual per capita income):
1) Low-income economies ($995 or less);
2) Lower-middle-income economies ($996 to $3,945);
3) Upper-middle-income economies ($3,946 to $12,195);
4) High-income economies ($12,196 or more).
For the purpose of the dummy variable Devi, the first three groups above are considered developing countries (Devi = 1), while the last group—high-income economics—is considered developed countries (Devi = 0).
Data on democracy has been compiled by the Economist Intelligence Unit since 2006. The third edition of the EIU’s Democracy Index reflects the situation as of November 2010. As described by the report, “the index provides a snapshot of the state of democracy worldwide for 165 independent states and two territories. [The index] is based on five categories: electoral process and pluralism; civil liberties; the functioning of government; political participation; and political culture. Countries are placed within one of four types of regimes: full democracies; flawed democracies; hybrid regimes; and authoritarian regimes” [8].
This paper uses EIU’s democracy type and overall score:
• Full democracies—score of 8 to 10
• Flawed democracies—score of 6 to 7.99
• Hybrid regimes—score of 4 to 5.99
• Authoritarian regimes—score of 0 to 3.99 For the purpose of the dummy variable Demi, the first two groups are considered here to be democracies (Demi = 1), while the last two groups are considered non-democracies (Demi = 0).
4. Estimation
The model and its different variants are estimated twice— once with OLS for countries where GINI data was available up to 1998, and once with 2SLS for the whole sample, including those countries with GINI coefficients after 1998. The use of an instrumental variable in the latter case is meant to deal with a potential endogeneity, since growth between 1998 and 2008 may have affected the GINI index measured within that period.
Table 1 presents the results of the OLS regression for the 100 countries that have GINI coefficients for 1998 or slightly before (1992-1998). This restriction is applied to avoid reverse causation from economic growth to inequality. The results confirm AR’s finding that “income inequality is negatively correlated with subsequent growth” [6]. The coefficient for the GINI variable is negative and statistically significant at the 1% level in all 7 columns (the t-statistics are also quite high). On average, a one standard-deviation increase in the GINI index results in 6%- 9% lower growth between 1998 and 2008. As more variables are added, the sample sizes decreases (only 72 countries have data on primary education or democracy).
The effect of initial per capita income in 1998 is small but negative and significant. The regressions including this variable also had higher adjusted R2 values, confirming AR’s point about using initial income per capita to control for convergence. As Barro puts it, “countries grow faster if they start poorer” [7]. Whether a country is developing or not has a large negative coefficient of -1.84 (significant at the 5% level), supporting Ray’s claim that the effect of inequality is much stronger in developing countries. The democracy dummy in Columns (5) and (6) is not statistically significant, implying that there is no difference in the rate of growth between democracies and dictatorships. The interactive democracy-GINI term in Column (7) is also statistically insignificant, supporting AR’s conclusion that there is no difference between democracies and non-democracies in terms of the relationship between inequality and growth.
In order to take advantage of the larger sample, the models were also estimated for all countries in the sample (including those with GINI coefficients up to 2005). To correct for a possible endogeneity bias (with growth affecting inequality), 2SLS regressions were used with primary school enrolment serving as the instrumental variable for GINI. This seemed a reasonable choice of instrument, since an unequal distribution of income is often correlated with unequal access to education, while the latter is not correlated with growth. Furthermore, as
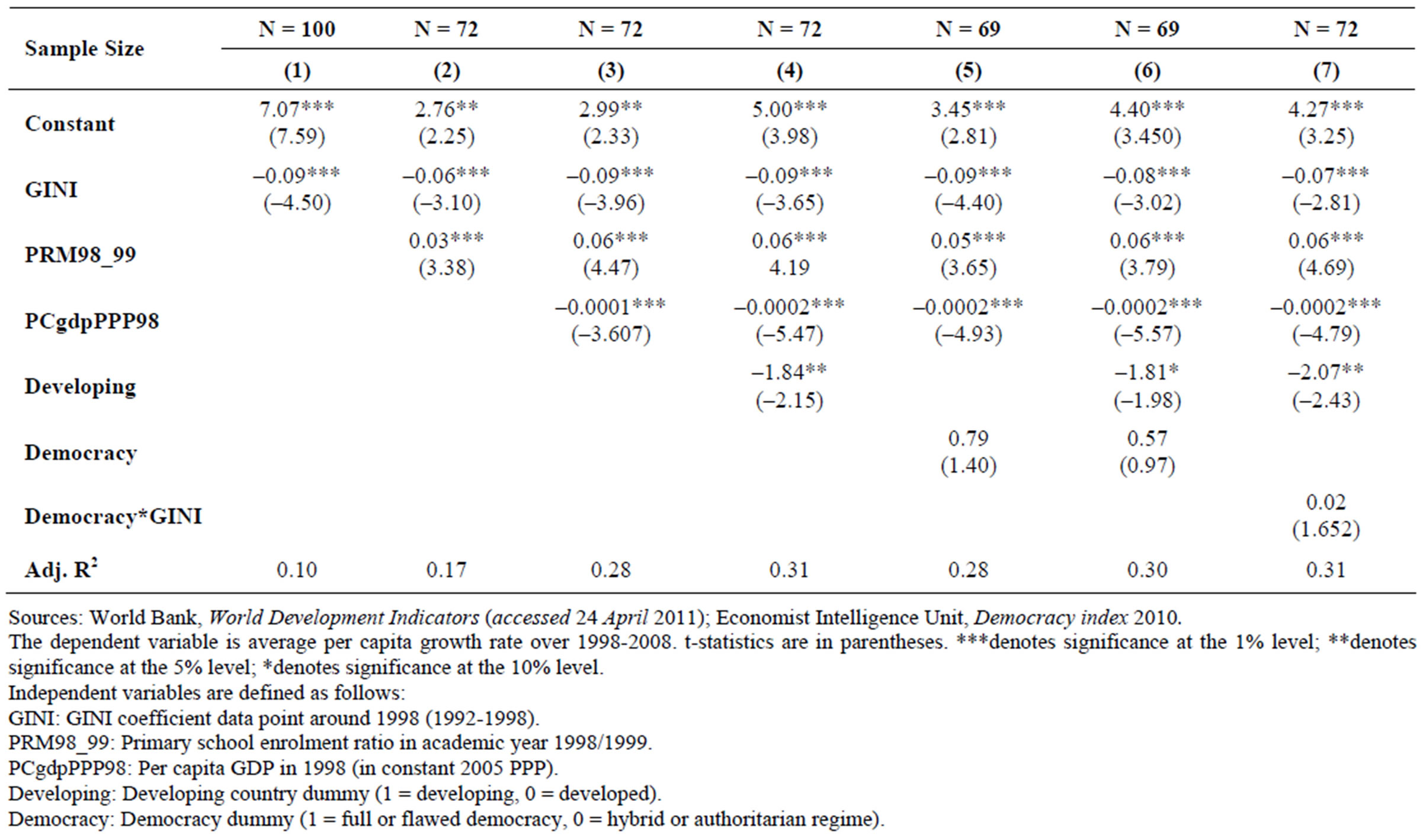
Table 1. Growth regressions for 1998-2008 using GINI coefficients up to 1998 OLS (heteroskedasticity-robust standard errors, variant HC1).
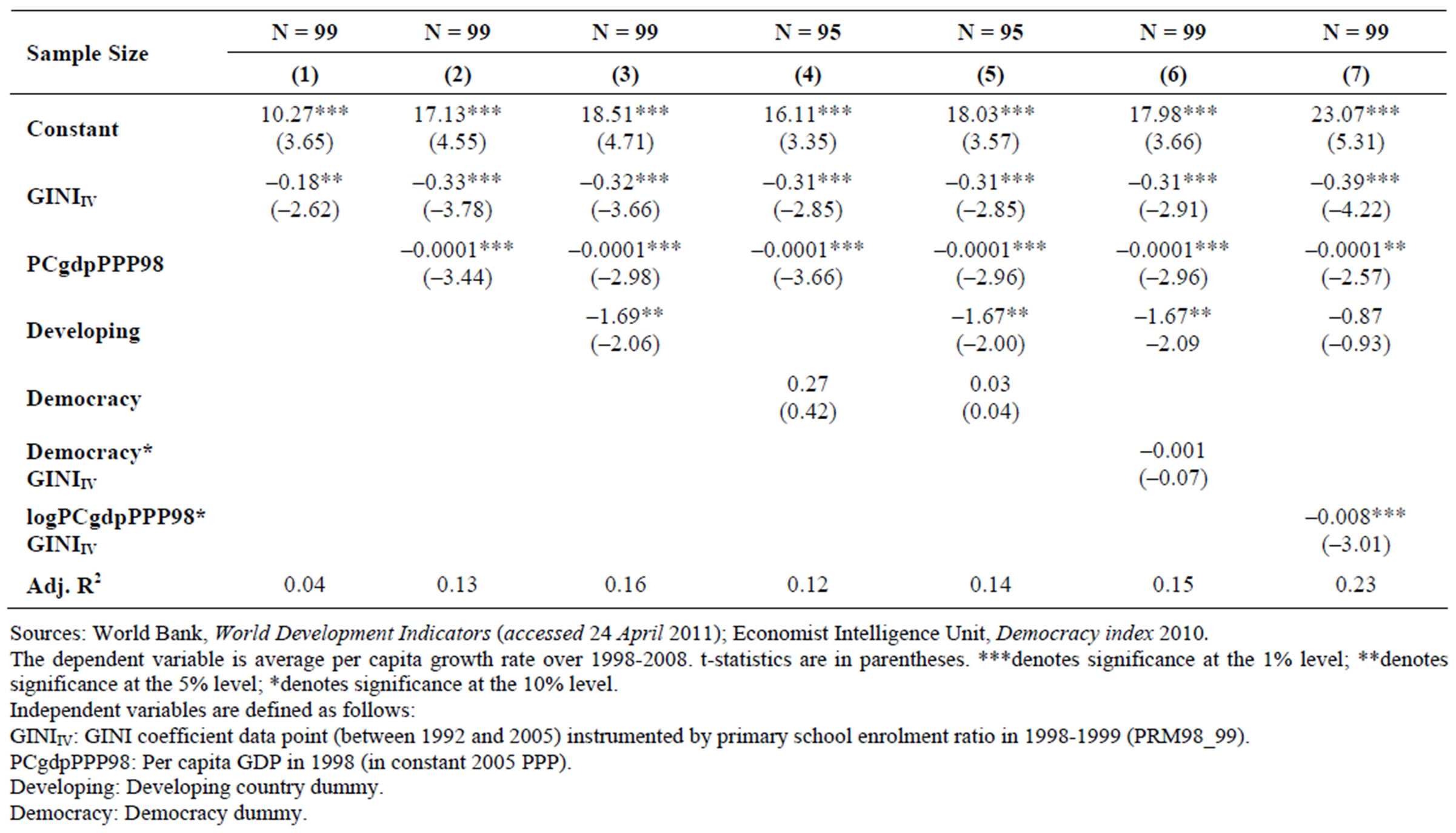
Table 2. Growth regressions for 1998-2008 using GINI coefficients between 1992 and 2005 2SLS (heteroskedasticity-robust standard errors, variant HC1).
the primary education data was measured for the 1998/99 academic year in all countries for which it was available, it precedes the growth period studied here and hence cannot affect the dependent variable directly.
Table 2 presents the results for the 2SLS regression, showing the instrumented GINIIV which was regressed on primary schooling in the first stage. The coefficients on the GINIIV variable are between 2 and 5 times higher than in the OLS regressions, likely the result of using a larger sample while controlling for endogeneity. They are all statistically significant at the 1% level, and imply an effect of up to 34% lower growth resulting from a one standard-deviation increase in the GINI index. The coefficient for initial per capita income is once again small but significant, allowing for convergence. The developing country dummy effect is a bit smaller (–1.69) than in the OLS results, but still negative and significant (at the 5% level). Once again, both the democracy dummy and the interactive democracy-GINI variable are not statisticcally significant, showing no difference—in terms of either the growth rate alone or the relationship of inequality of growth-between democracies and non-democracies.
Column (7) interacts the log of per capita GDP in 1998 with the GINIIV coefficient. Similar to Barro, the GINIIV itself is still strongly negative, but unlike Barro’s results, the coefficient for the interaction term here is also negative and significant (at 1%). This contradicts Barro’s conclusion that “the effect attenuates as per capita GDP rises” [7].
To further test Barro’s assertion that inequality affects growth negatively in poor countries but positively in rich ones, model (2) was estimated separately for developed countries (Devi = 0) and developing ones (Devi = 1). The result of the first regression (N = 31) was indeed positive, 1.08, but not statistically significant (t-stat = 1.278), while the second regression (N = 68) had a strongly negative coefficient –0.37, statistically significant at the 1% level (t-stat = –2.902). Thus there is no clear relationship between income inequality and subsequent growth in developed countries, while there is a negative and significant one in developing countries.
5. Concluding Remarks
The empirical results presented in Section 4 support the hypothesis that income inequality is negatively correlated with subsequent economic growth, at least in developing countries. Both the smaller sample with OLS and the larger sample with 2SLS showed a clear negative relationship. The effect was also stronger for developing countries in both cases. Democracy (or its absence) does not have a significant effect on either the relationship between inequality and growth or on the rate of growth itself, thus confirming that inequality creates pressures for redistribution in democracies and non-democracies alike. Furthermore, in contrast to Barro’s 2008 findings, inequality in developed countries does not seem to have a statistically significant positive affect on growth. The overall conclusion is that, beyond any moral objections to inequality, there are strong economic reasons to be concerned about it, as it retards growth under any political regime, at least in developing countries.
REFERENCES
- D. Ray, “Development Economics,” Princeton University Press, Princeton, 1998.
- R. J. Barro, “Inequality and Growth in a Panel of Countries,” Journal of Economic Growth, Vol. 5, No. 1, 2000, pp. 5-32. doi:10.1023/A:1009850119329
- A. K. Fosu, “Inequality and the Impact of Growth on Poverty: Comparative Evidence for Sub-Saharan Africa,” Journal of Development Studies, Vol. 45, No. 5, 2009, pp. 726-745.
- D. Qin, M. A. Cagas, G. Ducanes, X.-H. He, R. Liu and S.-G. Liu, “Effects of Income Inequality on China’s Economic Growth,” Journal of Policy Modeling, Vol. 31, No. 1, 2009, pp. 69-86. doi:10.1016/j.jpolmod.2008.08.003
- A. Castelló-Climent, “Inequality and Growth in Advanced Economies: An Empirical Investigation,” Journal of Economic Inequality, Vol. 8, No. 3, pp. 293-321. doi:10.1007/s10888-010-9133-4
- A. Alesina and D. Rodrik, “Distributive Politics and Economic Growth,” The Quarterly Journal of Economics, Vol. 109, No. 2, 1994, pp. 465-490. doi:10.2307/2118470
- R. J. Barro, “Inequality and Growth Revisited,” ADB Working Paper Series on Regional Economic Integration, No. 11, January 2008.
- Economist Intelligence Unit, “Democracy Index 2010: Democracy in Retreat,” London, 2010.
Appendix 1. List of Countries and Years for GINI Coefficients for Income—Full Sample.

