Journal of Electromagnetic Analysis and Applications
Vol.08 No.08(2016), Article ID:69982,19 pages
10.4236/jemaa.2016.88014
Relativity and the Solar Wind: The Maxwell-Equation Origins of the Solar-Wind Motional Electric Field
Joseph E. Borovsky1,2
1Space Science Institute, Boulder, CO, USA
2CSSE, University of Michigan, Ann Arbor, MI, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2016; accepted 20 August 2016; published 23 August 2016
ABSTRACT
The motional electric field of the solar wind as seen by the Earth is examined theoretically and with spacecraft measurements. As it flows outward from the sun, the solar-wind plasma carries a spatially structured magnetic field with it. To calculate the motional electric field of the solar wind the spatially structured magnetic field is Lorentz transformed; for a full physical understanding, it is also necessary to Lorentz transform the current densities and charge densities in the solar wind. Referring to Maxwell’s equations, two related questions are asked: 1) Is the source of the solar- wind motional electric field charge density in the solar wind, time derivatives of current densities in the solar wind, or both? 2) Is the solar-wind motional electric field at Earth an electrostatic field, an induction field, or a superposition of the two? A Helmholtz decomposition of the motional electric field of the solar wind is made into a divergence-origin (electrostatic) and a curl-origin (induction) electric field. The global electric field associated with the outward advection of the global Parker-spiral magnetic field is found to be electrostatic with its origin being a distributed charge density in the solar-wind plasma. The electrostatic versus induction nature of the time-varying electric field associated with the advection of mesoscale magnetic structure varies with time as differently shaped magnetic structures in the solar-wind plasma pass the Earth; the mesoscale structure of the solar-wind plasma contains sheets of space charge and sheets wherein the current density has nonzero time derivatives.
Keywords:
Lorentz Transformation, Electric Field, Induction, Helmholtz Decomposition, Solar Wind, Magnetic Structure, Heliosphere, Plasma

1. Introduction
The solar wind is a magnetized collisionless plasma comprised of ions (mostly protons) and electrons. (Collisionless means that inter-particle collisions that would disrupt the ion or electron orbits in the magnetic and electric fields are rare.) The solar-wind plasma flows at a high velocity radially outward from the Sun, in the range 250 km/s to 1000 km/s. Typical parameters for the solar wind at Earth appear in Table 1. The magnetic field B in the solar-wind plasma originates at the Sun and is carried outward with the supersonic plasma flow. Because of the rotation of the Sun and the radial outflow of the wind, the magnetic field in the solar wind has on average a “Parker-spiral” orientation [1] . The magnetic-field vector has strong localized variations about the Parker-spiral direction: these spatial variations in B are advected outward with the solar-wind flow [2] . Much of the spatial variation of B is owed to the presence of current sheets embedded in the solar-wind plasma [3] [4] , with the value of the magnetic-field vector B jumping across the current sheets.
The motional electric field E of a plasma is a Lorentz transformation of the magnetic field B in the plasma [5] . For a velocity vector v between two reference frames, the Lorentz transformation of the components of the electric and magnetic fields parallel to and perpendicular to v is [6]
 (1a)
(1a)
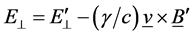 (1b)
(1b)
 (1c)
(1c)
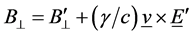 (1d)
(1d)
where 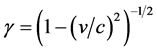 and where we will take the primed frame to be at rest in the solar-wind plasma and the unprimed frame to be the rest frame of the Earth or the Sun. In the rest frame of the solar-wind plasma,
and where we will take the primed frame to be at rest in the solar-wind plasma and the unprimed frame to be the rest frame of the Earth or the Sun. In the rest frame of the solar-wind plasma,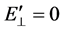 . This is because (in the absence of non-electromagnetic forces such as gravity) in a collisionless plasma particle orbit theory says that the ions and the electrons E-cross-B drift with an averaged velocity of
. This is because (in the absence of non-electromagnetic forces such as gravity) in a collisionless plasma particle orbit theory says that the ions and the electrons E-cross-B drift with an averaged velocity of 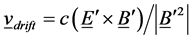 (cf. eq. (12.43) of Reference [6] ). In the rest frame of the plasma there can be no E-cross-B drift velocity of the ions and electrons, otherwise it would not be the rest frame of the plasma. Therefore, in the rest frame of the solar-wind plasma
(cf. eq. (12.43) of Reference [6] ). In the rest frame of the plasma there can be no E-cross-B drift velocity of the ions and electrons, otherwise it would not be the rest frame of the plasma. Therefore, in the rest frame of the solar-wind plasma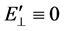 . In the reference frame of the Earth or the Sun, the plasma flow is of the order of v/c ~ 10−3, so γ @ 1 can be taken. For
. In the reference frame of the Earth or the Sun, the plasma flow is of the order of v/c ~ 10−3, so γ @ 1 can be taken. For 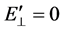 expression (1d) gives
expression (1d) gives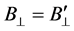 . For γ @ 1,
. For γ @ 1, 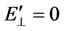 , and
, and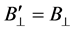 , expression (1b) yields the motional electric field E for a plasma moving with a velocity v in a magnetic field B to be
, expression (1b) yields the motional electric field E for a plasma moving with a velocity v in a magnetic field B to be
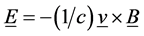 (2)
(2)
which is the low-velocity Lorentz transformation common for a moving conducting fluid [6] [7] . The solar-wind motional electric field as seen by the Earth (expression (2)) is often taken to be the driver of geomagnetic activity in the Earth’s magnetosphere-ionosphere system [8] (but see Reference [9] for a contrary interpretation).
In this paper, we wish to gain an understanding of the solar-wind motional electric field from first principles. The motional electric field of the solar wind will be examined via the Lorentz transformation of the magnetic-field structure in the solar wind. Because of the spatial variations of the magnetic-field vector B, the motional electric field will have spatial variations. Via Maxwell’s equations, the sources of the motional electric field will be sought: charge densities in the solar wind and time derivatives of current densities in the solar wind. The question will be asked whether the motional electric field of the solar wind is an electrostatic electric field, an
Table 1. Typical values (mean values) of solar-wind parameters at Earth.
inductive electric field, or both. We wish to gain an understanding of the solar-wind motional electric field from first principles. Identifying the electrostatic versus induction portions of electric fields within the Earth’s magnetosphere has been of interest because the identification yields an understanding of the origin of the electric fields and a capability to add them to numerical models of the magnetosphere [10] [11] .
To avoid confusion, the reader should note that there is also a non-motional electric field in the solar wind associated with the “interplanetary electrostatic potential” or “heliospheric electric potential” [12] . This is a global parallel-to-B electric field associated with the differences in the collisionless transport of the solar-wind electrons and the solar-wind ions along the magnetic field. The sign of this interplanetary electric field is outward along the magnetic field lines, accelerating ions away from the Sun and retarding the outward electron flux. This interplanetary electrostatic potential is responsible for the observed statistical increase of the bulk speed of the solar wind vsw between 0.3 AU and 1 AU. This interplanetary electrostatic potential is not the subject of the present study.
2. Electrostatic Fields versus Induction Fields and Charge Density versus Time-Varying Current Density
According to the Helmholtz decomposition [13] [14] , any vector field can be decomposed into the sum of an irrotational (curl-free) field plus a solenoidal (divergence-free) field. Hence, any vector electric field E can be written as the superposition
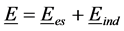 (3)
(3)
where Ees is an electrostatic electric field that is everywhere curl-free and Eind is an induction electric field that is everywhere divergence-free. Further, the field E can be determined everywhere in space from knowledge of the values of the divergence of the field E and the curl of the field E everywhere in space [14] . This determination of E from 







For this paper the following equivalence of adjectives for each of the two types of electric fields is declared. First type: inductive = divergence-free = solenoidal = non-potential = transverse. Second type: electrostatic = curl-free = irrotational = potential = longitudinal. For an electrostatic field Ees, the electric-field lines end; for an induction field Eind, the electric-field lines do not end.
Here we will define a purely electrostatic electric field Ees as an irrotational field having its origin in regions where the divergence 




it is seen that the electrostatic field originates from regions of nonzero charge density ρq. From Faraday’s law of induction

it is seen that the induction field originates from regions of nonzero ¶B/¶t. It is important to explore expression (5) a little further. Taking the curl of Faraday’s law






(with
The motional electric field 
3. Observations of the Solar-Wind Motional Electric Field at Earth
In Figure 1, the solar-wind speed and two components transverse to radial (from the Sun) of solar-wind motional electric field near Earth are plotted as functions of time for 100 days in the year 2004. The GSE (Geocentric Solar Ecliptic) right-handed coordinate system is used where X points from the Earth toward the Sun, Y points transverse to the Sun-Earth line in the ecliptic plane opposite to the direction of the Earth’s motion about the Sun, and Z is normal to the ecliptic plane pointing in the northward direction. In the top panel the solar-wind radial velocity vsw is plotted, in the middle panel and bottom panel the north-south component Ez and the dawn-dusk component Ey of the solar-wind motional electric field 
Figure 1. 100 days of the motional electric field E from the ACE spacecraft upstream of the Earth are shown. In the top panel the solar-wind speed vsw is plotted with 64-s time resolution. In the middle panel the north-south component of E is plotted: black points are 64-s time resolution and the red points are 24-hr running averages of the black points. In the bottom panel the dawn-dusk component of E is plotted: black points are 64-s time resolution and the red points are 24-hr running averages of the black points. The GSE coordinate system is used.
A higher-time-resolution look at the motional electric field of the solar wind appears in Figure 2. Here, plasma [18] and magnetic-field [19] measurements from the WIND spacecraft with 3-s time resolution are used to calculate
In the upper two panels of Figure 3 the vector tips of the solar-wind motional electric field 

Figure 2. The motional electric field of the solar wind is plotted for 2 hours of fast solar wind (top panel) and for 2 hours of slow solar wind (bottom panel). The 3-s time-resolution values are from the WIND spacecraft upstream of the Earth. Ey is in red and Ez is in blue. The GSE coordinate system is used.
Figure 3. In the top two panels the vector tips of solar-wind motional electric field at Earth are plotted in the (GSE) Ez-ver- sus-Ez plane. The plane is viewed from the Sun looking at the Earth. In the left panel 24-hr averages of E from OMNI2 are used and in the right panel 64-s resolution values of E from ACE are used. In the bottom two panels the vector tips of the solar-wind magnetic field are plotted, 24-hr averages from OMNI2 on the left and 64-s values from ACE on the right.
4. The Parker-Spiral Motional Electric Field
Owing to the 27-day rotation of the Sun, the magnetic field in the solar-wind plasma has a global Archimides- spiral pattern. In (r, θ, ϕ) spherical coordinates the Parker-spiral magnetic field B at the radius r from the Sun and colatitude θ in the heliosphere is given by [1]

where Bo is a reference magnetic-field strength near the Sun (with Bo > 0 for an out-of-the-Sun (away) field and Bo < 0 for an into-the-Sun (toward) field); ro is the reference radius where Bo is measured; ω » 2.9 ´ 10−6 radians/s is the angular rotation rate of the solar surface at the solar equator; and vsw is the solar-wind radial velocity. The angle θ = 0˚ at the north pole of the Sun and θ = 180˚ at the south pole. In general, the Parker-spiral magnetic field of the heliosphere is of one sector (away or toward) in the northern hemisphere of the heliosphere and is of the opposite sector (toward or away) in the southern hemisphere, with a heliospheric current sheet separating the two morphologies [21] . In Figure 4 the Parker-spiral motional electric field of the solar wind will be sketched with the heliospheric current sheet lying in the equatorial plane bounding an away sector (Bo > 0) in the northern hemisphere and a toward sector (Bo < 0) in the southern hemisphere.
For the Parker-spiral magnetic field given by expression (7), the motional electric field of expression (2) for a radial solar-wind velocity vsw = (vsw, 0, 0) is

Figure 4. As viewed from an observer in the ecliptic plane far from the Sun (yellow circle), Parker-spiral electric field lines are sketched in red and the charge density supporting that electric field is sketched in blue. North is toward the top. In this sketch the Parker-spiral magnetic field is away from the Sun in the northern hemisphere and toward the Sun in the southern hemisphere. The positively charged heliospheric current sheet is seen horizontally across the center of the sketch.

this electric field is sketched as the red field lines in Figure 4. The motional electric field E for the Parker spiral is purely poloidal: E is northward for an away-from-the-Sun magnetic-field orientation and E is southward for a toward-the-Sun magnetic-field orientation. Note in expression (8) that Eθ does not depend on vsw.
Examining expression (8) in spherical coordinates one finds 


a distributed charge density throughout the heliosphere. This charge density is sketched as the blue “+” and “−“ symbols in Figure 4. According to expression (9) the charge density is strong near the polar regions of the heliosphere (θ ~ 0˚ and θ ~ 180˚) and weak near the equatorial regions (θ ~ 90˚). For an away-from-the-Sun magnetic-field orientation (Bo > 0) the distributed charge density ρq is negative in the northern hemisphere and positive in the southern hemisphere and for a toward orientation (Bo < 0) the distributed charge density ρq is positive in the northern hemisphere and negative in the southern hemisphere. Note in expression (9) that ρq does not depend on the solar-wind velocity vsw.
With 

The distributed current density j in the solar-wind plasma that supports the global Parker-spiral magnetic-field geometry is calculated by applying Ampere’s law 


This distributed current density is purely radial and it is strong in the polar regions of the heliosphere and weak in the equatorial regions, with jr negative (toward the Sun) when the magnetic field is away from the Sun (Bo > 0) and jr is positive (away from the Sun) when the magnetic field is toward the Sun (Bo < 0).
Taking the heliospheric current sheet to lie in the equatorial plane of the heliosphere there is a radial component of the current in the sheet associated with the jump in the azimuthal component of the Parker-spiral magnetic field across the current sheet and there is an azimuthal current in the sheet associated with the reversal of the radial component of the magnetic field across the current sheet. Taking the thickness of the heliospheric current sheet to be d, Ampere’s law gives


for the magnitudes of the radial and azimuthal current densities in the heliospheric current sheet, note that the thickness d of the heliospheric current sheet could be a function of r, so the current density in the heliospheric current sheet could vary with r differently than the right-hand sides of expressions (11a) and (11b).
Note that the poloidal motional electric field of the solar wind reverses across the current sheet owing to the reversal of the direction of B across the sheet as vsw remains radially outward. This electric-field reversal across the current sheet is sketched in Figure 4. There is a nonzero charge density in the equatorial current sheet associated with the reversal of the poloidal electric field: Coulomb’s law gives this charge density ρq as

where again d is the thickness of the current sheet, and where again d could be a function of r. The charge density of the heliospheric current sheet is positive if the magnetic field is outward (from the Sun) in the northward hemisphere and inward in the southern hemisphere (as drawn in Figure 4): the charge density of the heliospheric current sheet is negative if the magnetic field is inward in the northern hemisphere and outward in the southern hemisphere. The source of this charge density is the relativistic transformation of current density into charge density [22] , which will be discussed in Section 5.1.
Owing to the orbital motion of the Earth around the Sun, the radial component Br of the Parker-spiral magnetic field gives rise to an additional north-south poloidal electric field as seen by the Earth. The orbital velocity of the Earth around the Sun is vorbit » 29.8 km/s in the dawnward direction, which is small compared with vsw and so the orbital motional electric field is small compared with the Parker-spiral motional electric field. The motional electric field 
In the real solar wind there are several complications to this ideal-Parker-spiral picture. First, the global solar wind contains solar ejecta, which are impulsively ejected large-scale plasmas with non-Parker-spiral-oriented magnetic fields. Second, the solar-wind velocity is not uniform everywhere: rather there are regions on the rotating Sun that emit fast wind and regions that emit slower wind, disturbing the uniform-Parker-spiral picture with compressions and rarefactions. Third, there is a tilt to the solar magnetic dipole, plus magnetic multipoles that invalidate the uniform-northern-hemisphere uniform-southern-hemisphere picture of Figure 4. Fifth, the heliospheric current sheet was drawn to be planar in Figure 4 but in reality it is tilted and warped. Finally, there are large-amplitude fluctuations in the magnetic-field orientation about the Parker-spiral direction representing a mesoscale spatial structure of the solar-wind magnetic field. This mesoscale structure is considered in the following section.
5. The Mesoscale Electric Field Structure of the Solar Wind
In this section, the mesoscale spatial structure of the solar-wind motional electric field in the reference frame of the Earth is examined. That electric-field spatial structure is associated with the mesoscale magnetic-field spatial structure of the solar-wind plasma, which is largely flux tubes separated by current sheets [3] [4] . The advection of these magnetic spatial structures past the Earth results in temporal variations of E and B at the Earth manifested as sudden large changes in the vectors E and B associated with each current sheet passing the Earth (cf. Figure 2).
5.1. Idealized Cases
The question of whether the mesoscale solar-wind electric field is an electrostatic field originating from charge density or an induction field originating from time-varying current density is first examined in two idealized cases drawn in the ecliptic plane in Figure 5. The first case (top panel) has the current sheets of the solar wind
Figure 5. Two idealized sketches in the ecliptic plane of the solar wind plasma advecting past the Earth with current sheets of infinite extent. In the top panel the current sheets of the solar wind (black) are oriented parallel to the solar wind velocity vector and in the bottom panel the current sheets of the solar wind are oriented with their normal parallel to the solar wind velocity vector. The direction of the solar-wind velocity is indicated in purple, the direction of the magnetic field is indicated in blue, and the direction of the motional electric field (in the Earth’s frame) is indicated in red. The motional electric field in the top panel is purely electrostatic (divergence origin, curl-free) and the motional electric field in the bottom panel is purely inductive (curl origin, divergence-free).
oriented along the Sun-Earth line and the second case (bottom panel) has the current sheets of the solar wind oriented normal to the Sun-Earth line. In both cases the plasma in the vicinity of the Earth is divided by two current sheets (black lines) into three plasmas, with the Earth within plasma #2. In both cases the solar-wind plasma is taken to have the uniform velocity vsw (purple vector) everywhere, with vsw parallel to the Sun-Earth line, with the Sun off the bottom of the drawing in the distance. In both cases plasma #2 is taken to have a strong uniform magnetic field B and plasmas #1 and #3 are taken to have weaker uniform magnetic fields B; the B vector (blue) is taken everywhere to be vertical out of the plane of the sketches with the strength of B changing across the current sheets.
In the top panel of Figure 5 the direction of the current density j in each current sheet is indicated by a green arrow, with the jump in the magnetic-field vector ∆B across the current sheet being related to the current density. In the reference frame of the Earth, the motional electric field in the solar wind is given by 





of the 3-vector current density j in a current density 4-vector (j, cρq) [22] [23] . (Of course the total charge is conserved in the Lorentz transformation, but the spatial volumes containing the ions and the electrons moving at different velocities in the nonzero current are Lorentz contracted differently, resulting in a nonzero charge density out of equal amounts of positive and negative charge [14] [23] .) As can be seen by examining the geometry of the electric field drawn in the top panel of Figure 5, there is no variation in E in the direction perpendicular to E, so

As an aside, note that if one applies the Lorentz transformation of expression (13) to the radial current density jr that supports the Parker-spiral magnetic field (expression (10)), then one gets the distributed charged density ρq (expression (9)) of the Parker-spiral electric field. Likewise, a Lorentz transformation of the current density in the heliospheric current sheet that corresponds to the reversal of the Parker-spiral magnetic field (expression (11a)) yields the charge density of the heliospheric current sheet that corresponds to the reversal of the Parker-spiral electric field (expression (12)). Again, those charge densities arise from a difference in the Lorentz contraction of the volumes containing the differently moving ions and electrons in the currents.
The second idealized case (bottom panel of Figure 5) has the current sheets of the solar wind oriented with the current-sheet normal vectors parallel to the solar-wind velocity vector vsw. In the sketch two current sheets (black) divide the region into three plasmas, with the magnetic-field strength of plasma #2 uniform and strong and the field strength in plasmas #1 and #3 uniform and weak. The velocity vsw (purple vector) is everywhere the same and so the motional electric field 

5.2. A Parker-Spiral-Aligned Flux Tube
The constructions in the two panels of Figure 5 were idealizations to produce a purely electrostatic motional electric field (top panel) and a purely induction motional electric field (bottom panel). In actuality the current sheets of the solar wind have a wide range of orientations [2] [4] [24] , and the current sheets are not infinite in extent [2] [24] . Usually, the magnetic field of the solar wind at Earth is approximately in the Parker-spiral orientation with the individual magnetic-flux tubes aligned approximately with the Parker-spiral direction [25] . In the top panel of Figure 6 a single Parker-spiral-oriented magnetic flux tube (pink) is sketched in the ecliptic plane at Earth. The magnetic field orientation (blue vectors) is away from the Sun inside the flux tube and the motional electric field in the reference frame of the Earth (red vectors) is northward directed up out of the ecliptic plane. The magnetic-field strength is sketched strong within the tube and weak outside of the tube so the motional electric field is strong within the tube and weak outside of the tube. In the bottom panel of Figure 6 the Parker-spiral-oriented flux tube of the top panel is viewed along the axis of the tube looking back along the spiral toward the Sun with the magnetic field pointed at the viewer. The up-down direction in the sketch of the bottom panel is the Earth’s north-south direction and the flux tube is drawn to have a square cross section. The direction of the current density in the current sheets (black) surrounding the pink flux tube is indicated with green vectors. In the reference frame with the Earth at rest, the tube and its surrounding plasma advects toward the right with the solar-wind velocity vsw away from the Sun; the projection of vsw is drawn as the purple vector in the bottom panel. The motional electric field 

Figure 6. In the top panel a Parker-spiral-oriented flux tube passing the Earth is sketched in the ecliptic plane; the magnetic field in the tube has an “away from the Sun” orientation. In the bottom panel the same flux tube is viewed looking down the axis of the tube back toward the Sun. In both panels the electric fields are sketched in the reference frame of the Earth.



In Figure 7, the Earth’s-reference-frame charge density 

Figure 7. For the flux tube drawn in the bottom panel of Figure 6 (with the magnetic field pointing up out of the plane of the figure) the electric fields in the Earth’s reference frame are numerically calculated. In the top panel the 



The superposition E = Ees + Eind of the two electric fields is calculated in the bottom panel: this superposed electric field E is the field that would be measured by a detector. In Figure 7 the tube is taken to have a uniform magnetic field B within the tube and zero magnetic field outside the tube. The current density j in each of the four current sheets bounding the tube is given by Ampere’s law to be jw = (c/4π)B, where w is the thickness of a current sheet. As is the case for the flux tube in the bottom panel of Figure 6, the flux tube in Figure 7 is taken to advect in the Earth’s frame from left to right with the solar-wind velocity and the magnetic field inside the tube points out of the page of the sketch. The charge density in the top and bottom current sheets is given by the relativistic transformation (taking γ = 1) 





A sampling of electric-field lines Ees(x) are numerically traced in the top panel of Figure 7. Note that these electrostatic-electric-field lines end. For the right and left current sheets of the flux tube the induction electric field Eind everywhere in space is numerically calculated from the Biot-Savart integrals applied to Faraday’s law of induction (expression (14b)) with the integration over ¶B/¶t in the right and left current sheets (e.g. eq. (5.14) of [6] )

A sampling of the induction electric-field lines are numerically traced and plotted in the second panel of Figure 7. Note that these induction-electric-field lines do not end. The vector sum (superposition) of the electrostatic field Ees and the induction field Eind is numerically calculated everywhere in space and a sampling of the field lines of this superposed field are plotted in the third panel of Figure 7. Note that the superposition Ees + Eind of the electrostatic field and the induction field is a uniform electric field within the flux tube and zero electric field outside of the flux tube (cf. expression (2)). Note also in the bottom panel of Figure 7 that the electric field lines begin and end on the top boundaries (where there is nonzero charge density) and that the tangential component of the electric field jumps across the left and right moving boundaries (where there is nonzero ¶j/¶t).
In the top panel of Figure 8 the ratio 
In the middle and bottom panels of Figure 8 the ratio 
Figure 8. For flux tubes similar to the one in Figure 7, the local value of the ratio 
local values of R are binning for all points inside the tall flux tube of the middle panel of Figure 8 (violet curve) and for all points inside the flattened flux tube of the bottom panel of Figure 8 (red curve); inside of the tall flux tube the induction electric field dominates almost everywhere and inside of the flattened flux tube the electrostatic electric field dominates almost everywhere.
Figure 9. For the three flux tubes of Figure 8, the local value of 
5.3. The Mesoscale Structure of the Solar Wind
In reality the mesoscale magnetic structure of the solar-wind plasma is quite complicated, resembling a “spaghetti” of tangled tubes of various cross-sectional shapes, various cross-sectional sizes, and various orientations [3] [4] . Instead of the idealized rectangular cross sections utilized in Section 5.2, the cross-sectional shapes of solar-wind flux tubes are more likely a Voronoi pattern of tubes packed against each other, each with a complicated polygonal shape (cf. Figure 1 of [4] ). Portions of current sheets that are obliquely aligned with the solar-wind velocity vector will have both 



6. Summary, Refinements, and Conclusion
A Helmholtz decomposition of the motional electric field in the solar wind was made and the electrostatic versus induction nature of the field was analyzed as was the charge-density origin versus the time-varying-current- density origin of the field. To calculate the motional electric fields, Lorentz transformations were used; when Lorentz transforming the electric and magnetic fields, the currents and charges also had to be Lorentz transformed. Just as the transformation of the motional electric field E from B is important at non-relativistic solar-wind velocities, the transformation of the charge density ρq from the current density j is important at non-re- lativistic velocities.
The large-scale time-averaged electric field of the solar wind associated with the outward advection of the Parker-spiral magnetic field in the solar-wind plasma is an electrostatic electric field having its source in the distributed charge density in the solar-wind plasma and the more-concentrated charge density of the heliospheric current sheet. This large-scale electric field is in the poloidal direction, northward at Earth in away magnetic sectors and southward at Earth in toward magnetic sectors. The origin of the large-scale electric field is a relativistic transformation of the large-scale magnetic field in the solar-wind plasma and the origin of the distributed charge density is the same relativistic transformation of the distributed current density in the solar-wind plasma that supports the Parker-spiral magnetic field.
The mesoscale structure of the solar-wind electric field spatially varies from being dominantly electrostatic to being dominantly inductive. At the Earth the time-varying electric field will be dominantly inductive near current sheets that have their normal vectors nearly aligned with the Sun-Earth line and the time-varying electric field will be dominantly electrostatic near current sheets that have their normal vectors nearly perpendicular to the Sun-Earth line. In general the mesoscale electric field will be a combination of electrostatic and induction electric fields, varying with time as differently shaped magnetic structures pass over the Earth. In compression regions of the solar wind time-varying induction fields will tend to dominate, and in rarefaction regions of the solar wind time-varying electrostatic fields will tend to dominate.
Note that in the actual solar wind the solar-wind velocity vector vsw also has spatial structure, on both large scales and mesoscales. On the mesoscale, there is usually a jump in the plasma velocity vector v as well as the magnetic-field vector B across the current sheets in the solar wind [27] . The jump in v across the current sheet amounts to a vorticity 

(Note that for charge density associated with vorticity there is no reference frame in which the charge density is zero.) In general the change in velocity ∆v across a solar-wind current sheet is much smaller in magnitude than the bulk flow velocity vsw of the solar-wind plasma, so the inhomogeneity of the flow-velocity field is typically a less-than-10% effect on magnitude of the motional electric fields of the solar wind.
To conclude, a first-principles understanding of the motional electric field of the solar wind associated with the advection of magnetic structure in the solar-wind plasma has been developed. This understanding is based on the Lorentz transformations of electric and magnetic fields, the Lorentz transformations of current densities and charge densities, and the application of Maxwell’s equations.
7. Discussion: Charge Density in the Solar-Wind Plasma
As seen in Sections 4 and 5, there is a nonzero charge density ρq in the solar-wind plasma associated with the motional electric field of the solar-wind: a distributed charge density associated with the advection of the global Parker-spiral magnetic field and more-concentrated charge densities in the current sheets of the solar wind. The physical origin of that charge density is the difference in the Lorentz contractions of volumes containing the positive ions of the solar wind and the negative electrons of the solar wind when the ions and electrons move at (slightly) different velocities owing to the presence of an electrical current. The differences in ion versus electron velocity are on the order of 1 km/s in the solar-wind current sheets.
The charge density in the solar-wind plasma associated with the motional electric field is frame dependent, being zero in the reference frame of the plasma and nonzero in other reference frames such as the frame of the Earth or the Sun.
In the directions perpendicular to B, the solar-wind plasma behaves on large scales as an ideal-MHD fluid: in the parallel-to-B direction the MHD description of the collisionless solar wind can fail (cf. Sect. 1 of [29] for MHD tests that are failed by the solar wind). Sometimes in space physics textbooks it is declared that MHD has 
In deriving ideal MHD, a quasineutrality condition np » ne (ion number density approximately equals the electron number density) is often assumed. The assumption of quasineutrality does not mean that Coulomb’s law 
For the charge density in the solar wind, one can assess just how quasineutral the solar-wind plasma is by calculating the fractional charge imbalance nq/no, where nq = ρq/e is the number density of excess charges and where no » np » ne is the number density of the plasma. A current sheet of the mesoscale structure of the solar wind plasma is considered. If the magnetic-field vector jumps by ∆B across the current sheet of thickness w, then the current density in the sheet is



This amount of charge imbalance is small, but it is not zero. Even with nq/no ~ 10−8 in the solar wind, the limit ρq = 0 cannot be taken and
Further, the condition of quasineutrality does not mean that the electric field is negligibly small. Certainly in calculating test-particle orbits in a plasma (or MHD fluid) both E and B are needed [40] . In Gaussian-cgs units the electric field E and the magnetic field B have the same units (1 gauss = 1 Stat Volt/cm = 1 gm1/2cm−1/2s−1) so their magnitudes are directly comparable: even though the magnitude of the motional electric field is v/c times smaller than the magnitude of the magnetic field (cf. expression (2)), the electric force on a particle qE is c/v times larger than the magnetic force q(1/c)v ´ B on a particle.
Acknowledgements
The author wishes to thank Joachim Birn, Mick Denton, Raluca Ilie, and Dan Welling for useful conversations. All spacecraft data utilized are freely available from NASA data servers http://cdaweb.gsfc.nasa.gov and http://omniweb.gsfc.nasa.gov. This work was supported at the Space Science Institute by the NSF Solar-Terre- strial Program via grant AGS-1261659, by the NASA Heliophysics LWS TRT program via grants NNX14- AN90G and NNX16AB75G, and by the NASA Heliophysics Guest Investigator Program via grant NNX14- AC15G and at the University of Michigan by the NASA Geospace SR&T Program via grant NNX12AD29G.
Cite this paper
Joseph E. Borovsky, (2016) Relativity and the Solar Wind: The Maxwell-Equation Origins of the Solar-Wind Motional Electric Field. Journal of Electromagnetic Analysis and Applications,08,133-151. doi: 10.4236/jemaa.2016.88014
References
- 1. Lemaire, J. and Scherer, M. (1971) Kinetic Models of the Solar Wind. Journal of Geophysical Research, 76, 7479-7490.
http://dx.doi.org/10.1029/JA076i031p07479 - 2. Griffiths, D.J. (1999) Introduction to Electrodynamics. 3rd Edition, Sect. 10.3 and Appendix B, Prentice Hall, Upper Saddle River.
- 3. Kusse, B.R. and Westwig, E.A. (2006) Mathematical Physics. 2nd Edition, Sect. 2.5.4, Wiley-VCH, Weinheim.
- 4. Noerdlinger, P.D. (1971) Boundary Conditions for Moving Magnetic Fields and Lorentz Transformation of Surface Currents. American Journal of Physics, 39, 191-192.
http://dx.doi.org/10.1119/1.1986090 - 5. McComas, D.J., Blame, S.J., Barker, P., Feldman, W.C., Phillips, J.L., Riley, P. and Griffee, J.W. (1998) Solar Wind Electron Proton Alpha Monitor (SWEPAM) for the Advanced Composition Explorer. Space Science Reviews, 86, 563-612.
http://dx.doi.org/10.1023/A:1005040232597 - 6. Smith, C.W., Acuna, M.H., Burlaga, L.F., L’Heureux, J., Ness, N.F. and Scheifele, J. (1998) The ACE Magnetic Fields Experiment. Space Science Reviews, 86, 613-632.
http://dx.doi.org/10.1023/A:1005092216668 - 7. Lin, R.P., Anderson, K.A., Ashford, S., Carlson, C., Curtis, D., Ergun, R., Larson, D., McFadden, J., McCarthy, M., Parks, G.K., Reme, H., Bosqued, J.M., Coutelier, J., Cotin, F., D’uston, C., Wenzel, K.-P., Sanderson, T.R., Henrion, J., Ronnet, J.C. and Paschmann, G. (1995) A Three-Dimensional Plasma and Energetic Particle Investigation for the WIND Spacecraft. Space Science Reviews, 71, 125-153.
http://dx.doi.org/10.1007/BF00751328 - 8. Lepping, R.P., Acuna, M.H., Burlaga, L.F., Farrell, W.M., Slavin, J.A., Schatten, K.H., Mariani, F., Ness, N.F., Neubauer, F.M., Whang, Y.C., Byrnes, J.B., Kennon, R.S., Panetta, P.V., Scheifele, J. and Worley, E.M. (1995) The WIND Magnetic Field Investigation. Space Science Reviews, 71, 207-229.
http://dx.doi.org/10.1007/BF00751330 - 9. King, J.H. and Papitashvili, N.E. (2005) Solar Wind Spatial Scales in and Comparisons of Hourly Wind and ACE Plasma and Magnetic Field Data. Journal of Geophysical Research: Space Physics, 110, A02104.
http://dx.doi.org/10.1029/2004JA010649 - 10. Hundhausen, A.J. (1995) The Solar Wind. In: Kivelson, M.G. and Russell, C.T., Eds., Introduction to Space Physics, Sect. 4.4, Cambridge University Press, New York, 91-128.
- 11. Podolsky, B. (1947) On the Lorentz Transformation of Charge and Current Densities. Physical Review, 72, 624-626.
http://dx.doi.org/10.1103/PhysRev.72.624 - 12. Gabuzda, D.C. (1987) Magnetic Force Due to a Current-Carrying Wire: A Paradox and Its Resolution. American Journal of Physics, 55, 420-422.
http://dx.doi.org/10.1119/1.15124 - 13. Malaspina, D.M. and Gosling, J.T. (2012) Two Spacecraft Observations of Magnetic Discontinuities in the Solar Wind with STEREO. Journal of Geophysical Research: Space Physics, 117, A04109.
http://dx.doi.org/10.1029/2011ja017375 - 14. Borovsky, J.E. (2010) On the Variations of the Solar-Wind Magnetic Field about the Parker-Spiral Direction. Journal of Geophysical Research: Space Physics, 115, A09101.
http://dx.doi.org/10.1029/2009ja015040 - 15. Borovsky, J.E. and Denton, M.H. (2016) The Trailing Edges of High-Speed Streams at 1 AU. Journal of Geophysical Research: Space Physics, 121, 6107-6140.
http://dx.doi.org/10.1002/2016ja022863 - 16. Borovsky, J.E. (2012) The Effect of Sudden Wind Shear on the Earth’s Magnetosphere: Statistics of Wind-Shear Events and CCMC Simulations of Magnetotail Disconnections. Journal of Geophysical Research: Space Physics, 117, A06224.
http://dx.doi.org/10.1029/2012ja017623 - 17. Borovsky, J.E. and Hansen, P.J. (1998) The Morphological Evolution and Internal Convection of E × B-Drifting Plasma Clouds: Theory, Dielectric-in-Cell Simulations, and N-Body Dielectric Simulations. Physics of Plasmas, 5, 3195-3223.
http://dx.doi.org/10.1063/1.872988 - 18. Borovsky, J.E. and Gary, S.P. (2009) On Viscosity and the Reynolds Number of MHD Turbulence in Collisionless Plasmas: Coulomb Collisions, Landau Damping, and Bohm Diffusion. Physics of Plasmas, 16, 082307.
http://dx.doi.org/10.1063/1.3155134 - 19. Parks, G.K. (1991) Physics of Space Plasmas. Sect. 5.4.4, Addison-Wesley, New York.
- 20. Gombosi, T.I. (1998) Physics of the Space Environment. Sects. 4.4 and 14.4.4, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511529474 - 21. Gurnett, D.A. and Bhattacharjee, A. (2005) Introduction to Plasma Physics with Space and Laboratory Applications. Sect. 6.1.3, Cambridge University Press, Cambridge.
- 22. Knipp, D.J. (2011) Understanding Space Weather and the Physics behind It. McGraw-Hill Learning Solutions, Boston.
- 23. Borovsky, J.E. (1998) Lightning Energetics: Estimates of Energy Dissipation in Channels, Channel Radii, and Channel-Heating Risetimes. Journal of Geophysical Research: Atmospheres, 103, 11537-11553.
http://dx.doi.org/10.1029/97JD03230 - 24. Jones, R.C. (1968) Return Stroke Core Diameter. Journal of Geophysical Research, 73, 809-814.
http://dx.doi.org/10.1029/JB073i002p00809 - 25. Ripoll, J.-F., Zinn, J., Colestock, P.L. and Jeffrey, C.A. (2014) On the Dynamics of Hot Air Plasmas Related to Lightning Discharges: 2. Electrodynamics. Journal of Geophysical Research: Atmospheres, 119, 9218-9235.
http://dx.doi.org/10.1002/2013jd020068 - 26. Maslowski, G. and Rakov, V.A. (2006) A Study of the Lightning Channel Corona Sheath. Journal of Geophysical Research: Atmospheres, 111, D14110.
http://dx.doi.org/10.1029/2005jd006858 - 27. Borovsky, J.E. (1995) An Electrodynamic Description of Lightning Return Strokes and Dart Leaders: Guided-Wave Propagation along Conducting Cylindrical Channels. Journal of Geophysical Research: Atmospheres, 100, 2697-2726.
http://dx.doi.org/10.1029/94jd00407 - 28. Dwyer, J.R. and Uman, M.A. (2014) The Physics of Lightning. Physics Reports, 534, 147-241.
http://dx.doi.org/10.1016/j.physrep.2013.09.004 - 29. Birn, J., Thomsen, M.F., Borovsky, J.E., Reeves, G.D., McComas, D.J., Bellian, R.D. and Hesse, M. (1997) Substorm Ion Injections: Geosynchronous Observations and Test Particle Orbits in Three-Dimensional Dynamic MHD Fields. Journal of Geophysical Research: Space Physics, 102, 2325-2341.
http://dx.doi.org/10.1029/96ja03032 - 30. Ilie, R., Daldorff, L.K.S. and Liemohn, M.W. (2015) Calculating the Inductive Electric Field in the Terrestrial Magnetosphere. Journal of Geophysical Research, 2015JA022034R.
- 31. Zaharia, S., Jordanova, V.K., Thomsen, M.F. and Reeves, G.D. (2008) Self-Consistent Geomagnetic Storm Simulation: The Role of Induced Electric Fields. Journal of Atmospheric and Solar-Terrestrial Physics, 70, 511-518.
http://dx.doi.org/10.1016/j.jastp.2007.08.067 - 32. Borovsky, J.E. and Birn, J. (2014) The Solar-Wind Electric Field Does Not Control the Dayside Reconnection Rate. Journal of Geophysical Research: Space Physics, 119, 751-760.
http://dx.doi.org/10.1002/2013JA019193 - 33. Goertz, C.K., Shan, L.-H. and Smith, R.A. (1993) Prediction of Geomagnetic Activity. Journal of Geophysical Research: Space Physics, 98, 7673-7684.
http://dx.doi.org/10.1029/92JA01193 - 34. Landau, L.D. and Lifshitz, E.M. (1960) Electrodynamics of Continuous Media. Sect. 49, Pergamon Press, New York.
- 35. Jackson, J.D. (1975) Classical Electrodynamics. 2nd Edition, Sects. 6.4, 6.5, 10.2, 11.10, and 12.4, Wiley, New York.
- 36. Alfven, H. and Falthammar, K.G. (1963) Cosmical Electrodynamics. 2nd Edition, Sect. 1.3, Oxford University Press, Oxford.
- 37. Borovsky, J.E. (2008) The Flux-Tube Texture of the Solar Wind: Strands of the Magnetic Carpet at 1 AU? Journal of Geophysical Research: Space Physics, 113, A08110.
http://dx.doi.org/10.1029/2007ja012684 - 38. Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E. and Bavassano, B. (2001) Identifying Intermittency Events in the Solar Wind. Planetary and Space Science, 49, 1201-1210.
http://dx.doi.org/10.1016/S0032-0633(01)00061-7 - 39. Weimer, D.R., Ober, D.M., Maynard, N.C., Burke, W.J., Collier, M.R., McComas, D.J., Ness, N.F. and Smith, C.W. (2002) Variable Time Delays in the Propagation of the Interplanetary Magnetic Field. Journal of Geophysical Research: Space Physics, 107, 1210.
http://dx.doi.org/10.1029/2001JA009102 - 40. Parker, E.N. (1965) Dynamical Theory of the Solar Wind. Space Science Reviews, 4, 666-708.
http://dx.doi.org/10.1007/BF00216273











