Journal of Electromagnetic Analysis and Applications
Vol.08 No.03(2016), Article ID:65062,9 pages
10.4236/jemaa.2016.83004
A Pulsed Electromagnet for Laser Wakefield Electron Acceleration Experiments
Septimiu Balascuta
ELI-NP Department, “Horia Hulubei” National Institute for R&D in Physics and Nuclear Engineering, Bucharest, Romania

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 December 2015; accepted 25 March 2016; published 28 March 2016
ABSTRACT
Laser Wakefield plasma acceleration of electrons to energies above 10 GeV, may be possible in the new high power Laser beam facilities. The design of an Electron Spectrometer with an electro- magnet with adjustable magnetic field is proposed for the characterization of electron energy spectrum with a precision better than 10% for the entire energy range from 0.5 GeV to 38 GeV. The expected precision in the measurement of the electron energy is calculated as a function of the magnetic field, of the electron energy and of the magnet length. To outline the advantages offered by a pulsed electromagnet with high magnetic fields, the mass and the electric power lost in the coils of a 4 m long electromagnet with continuous current and Iron yoke are calculated.
Keywords:
Electron Spectrometer, Electromagnet, Electron Beam, Magnetic Field, Pulsed Electric Current, DC Electric Current

1. Introduction
The Laser Wakefield Acceleration (LWFA) of electron beams [1] is based on the interaction of a focused Laser beam with intensity above 1018 W/cm2, with an under-dense plasma confined in a plasma channel with a diameter less than 1 mm. In the preformed discharged-based plasma channel [2] , plasma was produced by an electric discharge that was started at a few hundred nanoseconds before the arrival of Laser pulse. A 4.2 GeV pulsed electron beam, with only 6% energy spread was recently produced at the BELLA Laser Facility [3] , by focusing a 0.3 PW laser beam in a 9 cm long capillary plasma guide. At the European facility “Extreme Light Infrastructure Nuclear Physics” (ELI-NP), it is planned to focuse a 10 PW Laser beam (with 20 × 10−15 seconds per pulse and 200 Joules per pulse), with an F/40 parabolic mirror, in the center of the entrance edge of a capillary discharge guide up to 80 cm long, to accelerate electrons by LWFA [4] . The density of the gas in the capillary cell is planed to be varied between 1016 and 1019 cm-3. The first conceptual design of the Electron Specrometer (ES) proposed to be used for measurement of electron energies at ELI-NP was presented in [5] where the ES was proposed to be an assembly of a permanent magnet (2 m long) and a DC electromagnet with Iron yoke (1.5 m long). This work presents in Section 2 the most recent design of the ES considered at ELI-NP, for the energy measurements of pulsed electron beams with frequency 1 pulse/minute and maximum expected energy 38 GeV. In previous LWFA experiments [6] , the energy of electrons up to 1GeV was measured by passing the electron beam through the magnetic field in the gap between the two cylindrical poles of a broadband ES. The design of an electromagnet with DC current and Iron poles and yoke was the subject of many previous works. Fisher presented in [7] , general considerations of the design, construction, profile configurations and magnetic measurements of Iron dominated magnets. Basic expression for the optimum design of Iron core magnet was presented in [8] to reduce the energy dissipated in the coils. Uniform dipole, quadrupole, octupole fields and different magnet shapes were considered by G. Parzen [9] for the transport of the charged beam. However, for all the electromagnets with DC current and Iron yoke, the magnetic field cannot exceeded 2.5 Tesla due to the saturation of the Iron. To obtain a 5% precision in the energy measurement of electrons in the range [0.1 GeV, 38 GeV], the peak magnetic field of a 4 meters long electromagnet has to be about 3.5 Tesla (Section 2). Magnetic fields up to 8.4 Tesla, along the axis of 14.3 m long superconducting electromagnets were achieved at CERN [10] . Fields above 30 Tesla can be generated only by pulsed current electromagnets. Recently, a low-cost and transportable single-coil electromagnet that generated up to 110 Tesla peak field was built [11] . However, in magnetic fields above 100 Tesla, the coils are destroyed, making such electromagnets not attractive for the repetitive energy characterization of the electron beams. Compact table-top sources of coherent ultraviolet (UV) and X-Ray radiation can be built by combining undulators with very short period of the array of magnets and sources of LWFA electron beams [12] [13] . Very compact undulators with cryogenic permanent magnets [14] or superconducting coils with transversal field gradients [15] were built or are in construction. The electron beam passes through the undulators and emits X-Rays mainly along the forward direction of the beam. The undulators require electron beams with energy spread less than 0.1%. However, in two LWFA experiments [2] [3] , the electron beams had an energy spread above 1%. A proposed experimental set-up for LWFA of electrons at ELI-NP is presented in Section 2. The computed precision in electron energy measurements and the mass of the classical electromagnet with Iron yoke are presented in 2.1 and 2.2. An alternative ES proposed in this work, is a compact (0.5 m long) pulsed electromagnet with periodic pulsed currents, which meets the experimental requirements for the electron energy measurements at ELI-NP. To outline the advantages of the compact pulsed electromagnet, the computed precision of a DC electromagnet with B = 1T and Iron yoke is compared with that given by a 0.5 m long and 10 T pulsed electromagnet. The design of a pulsed electromagnet with a quadrupole focusing magnet is presented in Section 3. The pulsed electromagnet was designed for energy measurements of both electrons and positrons up to 40 GeV.
2. The Experimental Setup with Classical Electromagnet
The Electron Spectrometer (Figure 1) is a dipole magnet with two poles with length “L” and gap width “G”. The Laser beam is aligned with the axis of the capillary cell. The Z axis is parallel with the Laser beam axis.
X and Y axes are the horizontal and vertical axes normal to the axis of Laser beam. The magnetic field in the gap is almost uniform and aligned with the X axis. In Figure 1, the initial average momentum (P0) of the bunch of electrons makes an angle θ with the Z axis. The initial momenta directions of electrons are in the cone with angle 2α.
The diameter of the electron bunch along its trajectory increases with the distance traveled by electrons, due to the Coulomb interaction and to the electron beam intrinsic angular divergence (2α) expected to be less than 0.01 radians. In addition, the electron momentum can acquire a perpendicular component, if there is a small misalignment of the laser beam and capillary axes. In the horizontal XZ plane (of Figure 1) the misalignment angle θ between the initial momentum of the electrons and the axis of the capillary cell fluctuates from pulse to pulse.
Figure 2 presents the experimental set-up and the geometry of the Interaction Chamber (IC) with four meters long permanent dipole magnet, proposed at ELI-NP. The magnet is made from four segments, each one meter
Figure 1. The geometry of the dipole electromagnet is seen in the horizontal plane XZ through the Z axis of the gap (left figure) and in the vertical plane (XY) through the centre of the gap. The angular divergence of the bunch is 2α.
Figure 2. A view of the 450 cm long Interaction Chamber (IC), Auxiliary Chamber (AC), the Laser beam (red), focused by the F/20 parabolic mirror on the axis of the 100 cm long Plasma Discharge Guide (PDG), the Integrating Current Transformer (ICT), the 400 cm long Permanent Dipole Magnet (PDM), the horizontal (SP1a, SP1b) and vertical (SP2a, SP2b) scintillating plates, the 5 CCD cameras and the Beam Dump. All dimensions are in cm. The three electron trajectories (in blue) start from the exit of PDG, with the same energy and with different momentum directions.
long. The blue curved lines in Figure 2 are three electron trajectories starting from the center of the exit face of the plasma discharge guide, with the same energy but different initial momentum directions making angles +α, 0 and −α relative to Laser beam axis. These trajectories were used to calculate the length of the electron spots on first horizontal plate SP1a (at 20 cm below the magnet), and the first vertical plate SP2a (at 10 cm from the exit face of the magnet).
The charge of a few picoseconds long electron bunch is measured with the Integrating Current Transformer (ICT). The 4 meter long magnet starts at about 40 cm from the exit of the plasma discharge guide (PDG). The electrons with energy bigger than 200 MeV, exit from the 1 Tesla magnetic field inside the gap and interact with the horizontal and vertical Lanex plates SP1(a, b), SP2(a, b). The electron beam energy is calculated from the position of the beam spots on the two horizontal (or two vertical) SPs. The light emitted from the beam spots is collected and transported with lenses to the CCD cameras outside the IC. The CCD cameras are placed in Faraday cages that attenuate the electromagnetic pulse (EMP) emitted upon Laser interaction with plasma in PDG. The EMP has a broad range of frequencies (from tens of MHz up to tens of GHz). A dipole magnet with permanent magnets has a better field stability and zero power lost, compared with an electromagnet. The magnet requires an auxiliary chamber (AC, in Figure 2) located outside the IC such that the same vacuum pressure has to be in both chambers. The electron beam travels through the vacuum, such that the electron scattering on gas molecules and the bremsstrahlung radiation are reduced to a minim. The disadvantages of a 4 meter long magnet are the high cost for manufacturing and assembling and the long pump-down time of the total volume of IC and AC. For this reason, the idea to use a compact and less expensive electromagnet is very attractive. In order to provide the same precision in the energy measurements, the electromagnet has to have a peak magnetic field that is correlated with the magnet length and the gap width. Because the electron beam is divergent, the required width of the gap between the poles (G) increases with the length of the magnet (L), according to Equation (1) that was derived from the geometry of Figure 1, considering a uniform magnetic field. In this equation dx = 0.5 cm is the expected maximum uncertainty in the position of electron beam center at the exit of the PDG, along X axis.
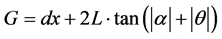 (1)
(1)
Considering the biggest value expected for the total angle 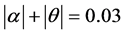 radians, the required gap width (G) is calculated for six lengths (L) of the electromagnet. In the same table Bmax is the peak magnetic field required for a 5% uncertainty in the energy measurements of electrons, with expected energy up to 35 GeV (Table 1).
radians, the required gap width (G) is calculated for six lengths (L) of the electromagnet. In the same table Bmax is the peak magnetic field required for a 5% uncertainty in the energy measurements of electrons, with expected energy up to 35 GeV (Table 1).
More precise calculations of required Bmax are presented in sections 2.1. For these calculations, the angle θ and the offset dx are zero. The results are obtained from numerical calculations in C codes, of three electron trajectories (Figure 2) starting from the center of the PDG exit and making angles +α, 0 and −α with the axis of the discharge guide. For the central trajectory (with α = 0), the initial electron momentum is along Z axis. Four α values (0.00625, 0.00125, 0.0025 and 0.005 radians) were considered. The calculations are done for 40 cm high Iron poles and considering a 0.4 m distance between the exit of the PDG and the start of the electrometer.
2.1. The Precision in Energy Measurement with a Classical Electromagnet
Compared with an electromagnet with continuous current (with a 20 cm gap and 4 m long poles), a pulsed electromagnet can be more compact because it provides a bigger field, only for a few miliseconds, a time window much bigger than the travel time of the electron beam. The peak field of a 1.5 meters long has to be 7 Tesla, in order to obtain a precision better than 10% in the energy measurements of the electron beam, for electron energies from 0.01 GeV to 38 GeV. The dependence of the precision on the magnetic field intensity is calculated in Figure 3(a), for a 2 m long electromagnet and 10 GeV, 20 GeV, 30 GeV, 40 GeV electrons. In Figure 3(b), the peak magnetic field required a 5% precision in electron energy is calculated versus the energy of the electron beam. A 4 meter long magnet has to reach a 3.5 Tesla field in order to assure a 5% precision in the energy measurements of 40 GeV electron beams with angular divergence less than 0.005 radians. The calculations were done for a magnetic field with a Gaussian profile along Y and Z axes, inside and outside the gap. According to both panels in Figure 3, if the peak field is 1 Tesla, the relative uncertainty is bigger than 10%, for the 38 GeV electrons. The dimensions of the electromagnet are constrained in principal by the space available in the Interaction Chamber, the mass load capacity of the cranes and the electric power available at the experimental facility.

Figure 3. The computed relative error for the electron energy measurements is calculated versus the magnetic field, for four energies of the electron beam with angular divergence ±0.0025 rad (in panel (a)). The length of the electron beam spot on the vertical plate (SP2) is calculated versus the electron kinetic energy for four angular divergences 2α of the beam (in panel (b)).
Table 1. The gap width (G), the length of the two poles (L), and the peak magnetic field Bmax (of the electromagnet) required for a 5% uncertainty of electrons with a 35 GeV energy. The poles are 30 cm high.
In Figure 3(a), the relative error ΔE/E was computed versus the magnetic field, from the y-coordinates of the electron spots for the three trajectories starting from the exit of capillary cell with the angle of initial momentum direction α = −0.0025, 0 and 0.0025 radians relative to the Z axis. The three trajectories intersect the SP1 plate in points with coordinates (Y1, Zsp1), (Y2, Zsp1) and (Yc, Zsp1) where Zsp1 is the Z-coordinate of the SP1 plate. The Y-coordinates depend linearly on the magnetic field. The linear fitting functions Y1(B) = a0 + b1∙B (for α = 0.0025 rad), Y2(B) = −a0 + b2∙B, (for α = −0.0025 rad) and Yc(B) = bc∙B, (for α = 0), were calculated from the y-coordinates (Y1, Y2, Yc) computed for 20 magnetic fields [1T, 2T, ... 20T] and a fixed energy E(MeV). The calculatins were done for energies between 1 GeV and 40 GeV, with a 1 GeV step. The parameter a0 was calculated from the intersection with SP1 plane of the electron trajectory starting with α = 0.0025. For the model function Y1(B), Y2(B), Yc(B) the only fitting parameters b1, b2 and bc were calculated for the 40 energies mentioned above. All three fiting parameters were invers proportional dependent on energy: b1(E) = a1/E, b2(E) = a2/E and bc(E) = ac/E. In the limit of the fitting errors, a1 , a2 and a3 were almost equal. The fitting parameters a0, a1, a2, a3 in the model functions Y1(E,B) = a0 + a1·B/E, Y2(E,B) = −a0 + a2·B/E and Yc(E,B) =ac∙B/E (where 1T ≤ B ≤ 20T, 1 GeV ≤ E ≤ 40 GeV) are presented in Table 2. For each electron energy, the absolute errors ΔE1 < 0 and ΔE2 > 0 were calculated from the equations Y1(E + ΔE1,B) = Yc(E,B) and Y2(E+ΔE2,B) = Yc(E,B). For each energy E and peak field B, the relative errors can be calculated from ΔE1/E = a1·B/(a3∙B − a0∙E) − 1 and ΔE2/E = a2·B/(a3∙B + a0∙E) − 1.
In Figure 4(a), the peak magnetic field required for a 5% precision in the energy measurements is computed versus the energy of the electron beam, for a 0.005 rad divergent beam and for six magnet lengths. For the same energy of the electron beam, the required peak magnetic field is smaller for the 4 m magnet than for the 2 m magnet.

Figure 4. (a) The magnetic field in the center of a dipole magnet, required for a 5% precision in electron energy measurement is computed versus the electron energy E (GeV), for six lengths of the magnet; (b) The relative error is calculated for 35 GeV electrons, for three lengths of the magnet, versus the magnetic field in the center.
Table 2. The fitting parameters a1, a2 and ac in the model functions Y1(E,B) = a0 + a1·B/E, Y2(E,B) = −a0 + a2∙B/E, Yc(E,B) = ac∙B/E where Y1,Y2,Yc are the y-coordinates of the electron spot in SP1 plate, for three electron trajectories (with α = −0.0025, 0 and 0.0025 radians). The dipole magnet pole is 0.4 m high and its length is Lmag.
The minimum energy of the electrons that can reach the vertical plate, increases with the length of the magnet. For a 4 meter long magnet, the precision in the energy measurements on the vertical plate, is 5% if the peak field is 3.5 Tesla in the center of the magnet. For 40 GeV electrons and a 2 m long magnet, the computed relative uncertainty is less than 10% if the magnetic field is 6 Tesla. The peak magnetic field required for a 5% measurement, decreases with the divergence of the electron beam (Figure 4(b)). Therefore, by reducing the divergence of the electron beam before it enters in the magnet, the values of the peak magnetic field and magnet length for the required 5%, can be both decreased. In this way, the mass and cost of the electromagnet are reduced. This solution is explored in section 3, where a quadrupole electromagnet is located in front of the magnet to focus the electron beam. The same pulsed electric current flow in the coils of the quadrupole and dipole electromagnets.
2.2. The Mass of the Electromagnet with Iron Yoke
The geometry of the electromagnet with an Iron yoke that can provide a return path for the fringe magnetic field up to 2 Tesla magnets is presented in Figure 5. For this geometry of the Iron yoke and Cu coils, the maximum field is about 2.2 Tesla, for a continuous current mode of operation. To increase the magnetic field intensity in the gap, the two Iron cores are joined with a C-yoke. At ELI-NP, the electromagnet will be located inside the Interaction Chamber where the space is limited. The C-type Iron Yoke is preferred, because it has a smaller volume than other geometries of the Yoke. A 2D model of such electromagnet was build in COMSOL®, to calculate the magnetic field (B0) in the centre of the gap as a function of the product of the number of turns per solenoid (Nw) and the current in wire (Iw). The calculations were done for seven wire gauges and for different number of turns Nw in solenoid. In Figure 6(a) and Figure 6(b) are the dimensions of the cross section in the XY plane of the coils. At the optimum ratio b/a = 2, the mass of the Iron Yoke that assures a given peak magnetic field in the gap, is a minimum. The space between the coils and the top of the Iron Yoke is 5 cm. In Figure 6, the magnetic field averaged over the area −10 cm < X < 10 cm and −10 cm < Y < 10 cm (in the XY plane) is plotted versus the product of the number of wires in a solenoid (NW) and the wire current (IW).
Figure 5. The geometry of the two dimensional COMSOL model of the Iron Yoke (green) and the coils (red) is seen in the XY plane. All the dimensions are in centimetres.

Figure 6. Left panel: The average magnetic field in the gap between two Iron poles is calculated versus the product of the number of turns per solenoid (Nw) and the current in wire (Iw), for 7 wire gauges, 20 cm wide gap and 40 cm high poles with C-yoke. Right panel: The field in the centre of the magnet B0(T) is calculated versus the total current in the solenoid for five gap width and 40 cm high Iron poles.
The calculations are done for a 40 cm high Iron poles and Cu wire with diameter 9.266 mm. Considering the product Nw∙Iw computed in Figure 6(a) for a 1 Tesla electromagnet, the mass of the Cu coils was calculated for four lengths of the electromagnet (1 m, 2 m, 3m and 4 m) versus the gap width in Figure 7(a). The mass of the Iron Yoke is presented in Figure 7(b), for the same range of gap widths.

Figure 7. The mass of Cu coils for a 1 m, 2 m, 3 m and 4 m long electromagnet with a 1 Tesla peak field and Iron Yoke with 40 cm high poles and Cu wire with diameter 9.266 mm, is calculated versus the gap width (left panel). The mass of Iron Yoke and poles is calculated versus the gap width, for 1 m , 2 m, 3 m and 4 m long Iron poles (40 cm high) and B0 = 1 Tesla in the centre of the gap and 9.266 mm diameter wires (right panel).
The mass of a 1 Tesla electromagnet has a small dependence on the wire gauge. For example, for a 4 meter long electromagnet, the mass is 48.1 tons for −1 AWG and 50.3 tons for a 3 AWG. The mass of an 1 meter long electromagnet is 9.14 tons for −1 AWG and 9.61 tons for 3 AWG. In order to decrease the mass of the electromagnet, a pulsed electromagnet with Iron cores and special Iron yoke, is proposed in Section 3. A pulsed electromagnet less than 1.5 meters can fit completely inside the Interaction Chamber. In this case, there is no need to extend the vaccuum volume, by attaching an AC to the IC, and the cost of the IC decreases significantly.
3. The Pulsed Electromagnet
A pulsed electric current in the coils of the electromagnet can be generated by the periodic discharge of a bank of capacitors. To decrease the power lost, the time window for the peak current has to be decreased to a minimum. The rising time for the electric current cannot be decreased below a minimum value that depends on the maximum current that has to be reached and to the available electrical power. The geometry of the pulsed electromagnet projected the top in the horizontal plane XZ and in the vertical plane YZ, can be seen in Figure 8(a) and Figure 8(b) respectively. Figure 8(c) presents the geometry of the quadrupole electromagnet.
The axis of the cylindrical plasma cell is aligned with the common axes of the dipole and quadrupole electromagnets. A water cooling system can be used to absorb the electric power lost in the coils, if the rising and falling times are both less than 10 seconds and the peak current stays constant for 2 milliseconds. This length of the time window when the peak current is constant is required for the synchronization between the arrival time of the Laser beam on the target capillary cell and the turn-on time of the CCD cameras for recording the images of the electron spot on the Scintillating Plates. The four lateral solenoids C1, C2, C3 and C4 increase the horizontal magnetic field in the center of the solenoid. The quadrupole magnet focuses the electron beam and decreases the dimensions of the electron spot on SP plates [16] . The blue and red arrows in Figure 8 indicate the direction of the magnetization in Iron and the direction of electric currents respectively. The dotted rectangles indicate the rectangular opening holes in the front and back Iron walls, required for the passage of Laser beam. The bottom scintillating plates (SP2) are fixed on the vacuum Aluminum flange. The length of the magnet “L” is bigger than the length of the Iron poles “d” because the Iron yoke is closed in the horizontal plane of the Laser beam.
Due to the Coulomb interaction between the electrons in a bunch and to the initial divergence of the electron beam, the diameter of the electron bunch increases with the distance travelled by the electron beam. Precise measurements of the electron energy are possible if the two diameters of the electron spot along X and Z directions are small. The diameter of the electron spot along Z axis is proportional with the difference Z2 − Z1 between the Z-coordinates of the intersection points of the electron trajectories on horizontal SP1 plates. For comparison, the calculations were done for a 1 T, 4 m long DC electromagnet (Figure 9(a)) and for a 5T, 0.5 m long pulsed electromagnet (Figure 9(b)). In both cases, the entrance face of the electromagnet is at 40 cm distance

Figure 8. In panel (a) is presented the top view of the pulsed electromagnet with copper coils (red) and Iron yoke (green). In (b), the magnet is seen in the vertical plane through magnet center. In (c), The geometry of the qadrupole electromagnet, is seen from the exit of plasma cell in panel (c).

Figure 9. The length of the electron beam spot on the horizontal plate (SP1) is calculated for a 1 Tesla, 4 m long magnet (panel (a)) and for a 10 Tesla, 0.5 m long pulsed electromagnet (panel (b)).
from the exit of the capillary cell.
The geometry of the coils and Iron yoke of the pulsed electromagnet was designed to minimize the fringe magnetic field in the volume of the target (PDG). The Cu coils wound around the Iron poles, can carry pulsed electric currents with flat-top profile and a peak current intensity that is constant only in a few milliseconds time window. The magnetic field profile along the Z axis is expected to focus the beam of electrons, such that the dimensions of the electron spot are a minimum.
4. Conclusions
The calculated mass of a 4 meter long electromagnet (with a 1.2 T field in the centre) exceeds 8 tons if the magnet is over 1.5 meters long. One proposed solution is a pulsed electromagnet made from quadrupole and a dipole electromagnets aligned along a common axis parallel with the axis of plasma guide. The quadrupole magnet has to be located in front of the dipole magnet. The mechanical support for each electromagnet has to be strong enough to overcome the repulsive forces between them. The 0.5 meters long pulsed electromagnet presented above is much less heavier than a 4 meter long electromagnet. This simplifies the transport and installation of the electromagnet. The direction of the electric currents in the lateral coils is chosen such that the magnetic field lines are closed through the Iron, and decrease the fringe magnetic field profile. A zero fringe field over the volume of the capillary gas cell is required in the LWFA experiments, where the initial direction of the electron beam has to be parallel with the axis of the capillary cell.
The precision in measurement of the position of the electron spot depends on the dimensions of the spot. On the horizontal SP plates, the length of the spot increases with the length of the electromagnet. The field of the quadrupole magnets decreases the length of the electron spots on the vertical SP plates, in the vertical direction. The light emitted from the spot has to be high enough to assure a good ratio signal/noise for the measurements of the spot position. The brightness of the electron beam spot decreases with the increase in the spot diameter. Because the experiment requires a precision of less than 5%, the length of the pulsed electromagnet is less than 1 meter.
Acknowledgements
The research work leading to these results was supported by the “Extreme Light Infrastructure Nuclear Physics (ELI-NP) Phase I”, a project co-financed by the Romanian Government and European Union through the European Regional Development Fund.
Cite this paper
Septimiu Balascuta, (2016) A Pulsed Electromagnet for Laser Wakefield Electron Acceleration Experiments. Journal of Electromagnetic Analysis and Applications,08,33-41. doi: 10.4236/jemaa.2016.83004
References
- 1. Nakamura, K., Gonsalves, A.J., Lin, C., Smith, A., Rodgers, D., Donahue, R., Byme, W. and Leemans W.P. (2011) Electron Beam—Charge Diagnostics for Laser Plasma Accelerators. Physical Review Special Topics—Accelerators and Beams, 14, 062801(1-9).
http://dx.doi.org/10.1103/PhysRevSTAB.14.062801 - 2. Nakamura, K., Nagler, B., Tóth, Cs., Geddes, C.G.R., Schroeder, C.B., Esarey, E., et al. (2007) GeV Electron Beams from a Centimeter-Scale Channel Guided Laser Wakefield Accelerator. Physics of Plasmas, 14, 056708.
http://dx.doi.org/10.1063/1.2718524 - 3. Leemans, W.P., Gonsalves, A.J., Mao, H.-S., Nakamura, K., Benedetti, C., Schroeder, C.B., et al. (2011) Multi-GeV Electron Beams from Capillary-Discharge-Guided Subpetawatt Laser Pulses in the Self-Trapping Regime. Physical Review Letters, 113, 245002.
http://dx.doi.org/10.1103/PhysRevLett.113.245002 - 4. Turcu, I.C.E., Balascuta, S., Negoita, F., Jaroszynski, D. and McKenna, P. (2015) Strong Field Physics and QED Experiments with ELI-NP 2 × 10 PW Laser Beams. AIP Conference Proceedings, 1645, 416.
http://dx.doi.org/10.1063/1.4909613 - 5. Balascuta, S. and Turcu, I.C.E. (2015) A Conceptual Design of an Electron Spectrometer for ELI-NP. AIP Conference Proceedings, 1645, 296.
http://dx.doi.org/10.1063/1.4909589 - 6. Nakamura, K., Wan, W., Ybarrolaza N., Syversrud, D., Wallig, J. and Leemans, W.P. (2008) Broadband Single-Shot Electron Spectrometer for GeV-Class Laser-Plasma-Based Accelerators. Review of Scientific Instruments, 79, 05330.
http://dx.doi.org/10.1063/1.2929672 - 7. Fisher, G.E. (1987) Iron Dominated Magnets. AIP Conference Proceedings, 153, 1120-1227.
http://dx.doi.org/10.1063/1.36376 - 8. Biranti, G. and Gabriel, M. (1970) Basic Expressions for Evaluating Iron Core Magnets—A Possible Procedure to Minimize Their Cost. CERN/SI/Int. DL/70-10.
- 9. Parzen, G. (1976) Magnetic Fields for Transporting Charged Beams. BNL 50536.
- 10. Rossi, L. (2009) Superconductivity: Its Role, Its Success and Its Setback in the Large Hadron Collider (LHC). 9th European Conference on Applied Superconductivity, 13-17 September 2009, Dresden, [CERN-ATS-2010-006].
- 11. Potugall, O., Puhlmann, N., Müller, H.U., Barczewski, M., Stolpe, I., Thiede, M., et al. (1997) The Design and Performance of a Transportable Low-Cost Instrument of Magagauss Field. Journal of Physics D: Applied Physics, 30, 1697-1702.
http://dx.doi.org/10.1088/0022-3727/30/11/020 - 12. Gruner, F., Becker, S., Schramm, U., Eichner, T., Fuchs, M., Weingartner, R., et al. (2007) Design Considerations for Table-Top Laser-Based VUV and X Ray Free Electron Lasers. Applied Physics B, 86, 431-435.
http://dx.doi.org/10.1007/s00340-006-2565-7 - 13. Jaroszynski, D.A., Bingham, R., Brunetti, E., Ersfeld, B., Gallacher, J., van der Geer, B., et al. (2006) Radiation Sources Based on Laser Plasma Interactions. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 364, 689-710.
http://dx.doi.org/10.1098/rsta.2005.1732 - 14. O’Shea, F.H., Marcus, G., Rosenzweig, J.B., Scheer, M., Bahrdt, J., Weingartner, R., et al. (2010) Short Period High Field Cryogenic Undulator for Extreme Performance of X-Ray Free Electron Lasers. Physical Review Accelerators and Beams, 13, 070702.
http://dx.doi.org/10.1103/PhysRevSTAB.13.070702 - 15. Rodriguez, V.A., Bernhard, A., Keilmann, A., Peiffer, P., et al. (2013) Development of a Superconducting Transverse-Gradient Undulator for Laser Wakefield Accelerators. IEEE Transactions on Applied Superconductivity, 23, 4101505.
http://dx.doi.org/10.1109/TASC.2013.2240151 - 16. Balakin, V. (1995) Focusing a Submicron Beam for a TeV Scale e+ e− Linear Colliders. Physical Review Letters, 74, 2479-2482.
http://dx.doi.org/10.1103/PhysRevLett.74.2479





