Journal of Electromagnetic Analysis and Applications
Vol.07 No.06(2015), Article ID:57248,8 pages
10.4236/jemaa.2015.76020
Measurable Dielectric Permittivity Range for TE and TM Modes in a Shielded Dielectric Resonator
Eduardo Javier Paez1, Roberto Cessare Callarotti2, Yuande Sanchez3
1Centre for Quantum Technologies, National University of Singapore, Singapore City, Singapore
2Instituto Venezolano de Investigaciones Científicas (IVIC), Caracas, Venezuela and Universidad del Turabo, Gurabo, Puerto Rico
3Fundación Instituto de Ingeniería, Caracas, Venezuela
Email: ejpaezb@nus.edu.sg, robercallarotti@gmail.com, sanchez@fii.gob.ve
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 April 2015; accepted 15 June 2015; published 18 June 2015
ABSTRACT
Dielectric resonator methods constitute one of the most useful techniques for the measurement of electromagnetic material properties in the microwave frequency range. Several geometric configurations are used for this purpose and, in the present paper, we consider the case of a dielectric rod enclosed in a cylindrical metallic enclosure. To carry out dielectric measurements in this system it is necessary to know the highest permittivity constant value for which the resonance condition still can be attained into the cavity. Using an approach based on magnetic and electric Hertzian potentials we have derived the set of TE and TM modes for the relevant geometry described and, then we have calculated the valid dielectric permittivity constant range of measurements for low-loss materials in a cylindrical cavity using a simple resonance frequency condition. Finally, we present a simple application of this method in order to determine the dielectric permittivity constant of heavy oil with 11 API.
Keywords:
Dielectric Resonator, Hertzian Potential, Cylindrical Cavity, Electromagnetic Characterization, Dielectric Permittivity Constant Measurement

1. Introduction
When dielectric measurements are performed in a shielded dielectric resonator, the shift of the resonant frequency caused by the presence of the sample (with a given dimension and dielectric permittivity constant), must be taken into account. The electromagnetic field must satisfy the boundary conditions required at the metal shielding (usually assumed as a perfect electric conductor) and at the material sample, thus obtaining a standing wave inside the cavity. The resonant frequency of this configuration decreases with respect to the resonant frequency of the empty cavity because the electric field increases due to the presence of a low loss dielectric material, so that forcing the wavelength to be smaller in order to achieve the border condition at the metal enclosure. For any specific combination of the diameter and the dielectric permittivity constant (see Figure 1) of the central material there is a cut-off frequency which below that it is possible to have a resonant condition. Above this frequency the cavity will exhibit a high impedance at the excitation port so that any electromagnetic mode practically disappears. Thereby, it is necessary to know the value of the highest dielectric permittivity constant which could be measured in the cavity for a given radius of the central rod.
In this paper we employ the formalism of the Hertzian potentials to find the electromagnetic solution of this configuration. Then we determine the limit of the real dielectric permittivity constant by numerically solving the nonlinear electromagnetic equations, thus obtaining the wave number in both materials inside the cavity (dielectric rod and air) and independently calculating the frequency inside those volumes.
Hertzian potentials have been used to solve different electromagnetic problems: in the study of the properties of aperture array systems [1] , non-linear waveguides [2] , Green’s functions for multilayered media [3] and electromagnetic wave interaction with nanodevices [4] . They have also been applied for the determination of TE and TM modes of circular cylindrical cavities using magnetic-type and electric-type Hertzian potentials res- pectively [5] . Figure 1 shows the case of a cylindrical dielectric resonator enclosed by a metal shield, where b is the radius of the outer cylinder, a is the inner resonator radius and d is the height (length of the structure). The configuration can be regarded as a cylindrical waveguide enclosing a central sample of radius a, and terminated by perfectly conducting planes. The general solution for the axial E field in TM modes was discussed in [6] , proposing a general solution for the axial E field for TM modes.
In [7] the solution of this system was obtained by solving directly Maxwell’s equations and substituting the corresponding zero axial component of magnetic or electric field for TE or TM mode respectively. A similar approach was presented in reference [8] . The aforementioned methods have the disadvantage that the cut-off wave number appears in the denominator of the total power flow equation implying a contradiction since it means that the power will vanish when the radius is very small. This contradiction is solved by including a factor in the numerator which depends on the cut off wave number, as proposed by [9] for a similar system.
The electromagnetic field in the material sample (region 1) and in air (region 2) are determined by using the relevant Hertzian potentials in their general mathematical form. The proper boundary conditions are then applied to the derived equations which can then be solved numerically. In practice, the resonant frequency and the system quality factor are measured then to determine the electromagnetic properties of materials [6] [7] [10] - [12] .
In this paper we first present a brief introduction to Hertz’s potentials, and then we apply this theory to the classical case of a cylindrical waveguide [5] . We then discuss the waveguide which includes the central cylindrical sample. Finally we discuss the usable range of this experimental arrangement in the determination of dielectric and magnetic properties.
2. Hertzian Potentials
In a charge free region with constant permittivity, the divergence of E is zero, thus implying that this field can
Figure 1. Shielded dielectric resonator.
be expressed as the curl of an auxiliary vector potential. This is the base for Hertz potential formulation [13] . For a homogeneous, isotropic, and charge-free region, E can be determined from the curl of an auxiliary vector potential  defined as magnetic-type Hertzian potential. Thus,
defined as magnetic-type Hertzian potential. Thus,
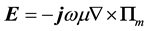 (1)
(1)
Then from Maxwell’s equations,
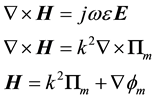 (2)
(2)
where  is an auxiliary scalar potential, and
is an auxiliary scalar potential, and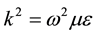 .
.
Now, we can use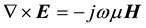 , and substituting (1), we obtain:
, and substituting (1), we obtain:
 (3)
(3)
Using the following identity 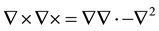 and combining (2) and (3), we obtain:
and combining (2) and (3), we obtain:
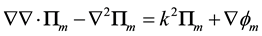 (4)
(4)
Since 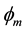 is an auxiliary scalar potential we can select
is an auxiliary scalar potential we can select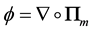 , obtaining the following Helmholtz equation,
, obtaining the following Helmholtz equation,
 (5)
(5)
A second Helmholtz equation can be obtained from the fact that the divergence of H is always zero. This fact can be expressed in terms of the curl of another vector potential 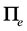 called electric-type Hertzian potential. As in the previous case, the same analysis applies for the TM modes where the electric-type Hertzian potential should be used [13] . The magnetic field can be expressed as,
called electric-type Hertzian potential. As in the previous case, the same analysis applies for the TM modes where the electric-type Hertzian potential should be used [13] . The magnetic field can be expressed as,
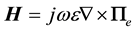 (6)
(6)
Using Maxwell’s equations and combining with (6), we obtain,
 (7)
(7)
where 

3. TE and TM Modes for the Cylindrical Cavity Resonator
3.1. Solution for TE Modes
In the case of TE modes, if we observe the magnetic-type Hertzian potential, the only way to generate a zero component in longitudinal axis of E field is that the Hertzian potential has zero components in radial and azimuthal direction. It means that magnetic-type Hertzian potential can be expressed like:

In the case of resonators the perfect conductor boundary conditions at 




Due to this fact, when the cavity geometry coincides with the coordinate system, we can use the separation variable method in order to achieve the boundary conditions [14] . Then,

Substituting (11) in (5), we obtain the Bessel differential equation

A possible P dependence with 



The differential equation shown above is known as the Bessel Differential Equation, whose general solution is,

where, 


The Helmholtz wave Equation (5) is valid for both regions of the shielded resonator, with the requirement that in the enclosed section 







It is important to note that


The boundary conditions of the tangential electric field at 





Solving for B and C in (18), substituting it in (19) and (20), and then dividing side by side these two ex- pressions, we can obtain the following relation,

where

By making

Equations (21) and (23) give the relation between the electromagnetic parameters of the unknown medium and the resonant frequency. The cut off wave number can be determined if the dielectric permittivity constant is known or viceversa. This system is solved numerically using the Matlab function fsolve. The solution given in Equation (21) reduces to the simple form given in [15] and [6] when


3.2. Solution for TM Modes
The treatment is similar for TM modes but using electric-type Hertzian potential as was presented on page 3. The general solution for this potential is in principle the same as in (15). E and H fields can be obtain using (6) and (7) and after applying the electromagnetic edge conditions, it gives,

where,

It is also worth pointing out that for this given circular symmetry of the set of E and H fields, which is easily appreciable in the corresponding Hertzian potentials (15), we can expect pure TE and TM as stated in [21] .
4. Convergence Range for Dielectric Measurements
Previously, we have mentioned that the frequency in both regions (air and dielectric) must be equal in order to represent a real resonant condition. However since we set 
We now exemplify our statement with an example. Consider a resonant frequency calculation for TE and TM modes in a circular cylindrical cavity resonator with a central dielectric rod. In the Table 1 it is considered the case of two empty cavities designed for the TE011 and TM011 modes respectively with a resonant frequency of 5 GHz, being twice the radius a of the length d. See the Figure 1.
For a given dielectric permittivity constant/radius of the central cylinder, the resonant frequency is calculated as solution of the corresponding TE or TM equations set. Thus, for a selected working mode order n and a fixed radius of the dielectric rod, the resonant frequency decreases when we increase the dielectric permittivity con- stant. Then we reach a value of permittivity where the wave numbers 

In the following we have determined the usable range for the Cavity 1 and Cavity 2. This is shown in Figures 2-4 for the set of modes 011, 021 and 031 respectively, where we have determined the dependence of the resonance frequency with respect to the dielectric permittivity constante of the central sample under mea- surement for a fixed radius. In the case of TE modes, Cavity 1, the cutoff relative dielectric permittivity constant are


Table 1. Cavity design for TE modes.
Table 2. Higher order modes of the TE/TM011 for cavity 1: 5.000 GHz and cavity 2: 5.000 GHz.
Figure 2. Usable range for dielectric measurement for (a) Cavity 1 TE011; (b) Cavity 2 TM011. In both cases it can be appreciated the breaking point of the resonant condition for this particular mode. TM011 mode has a higher measurable range for dielectric permittivity constant than TE011 mode.
Figure 3. Usable range for dielectric measurement for: (a) Cavity 1 TE021; (b) Cavity 2 TM021. It can be noticed that the measurable range is higher than for the previous mode. In this case both ranges are of similar length.
Figure 4. Usable range for dielectric measurement for: (a) Cavity 1 TE031; (b) Cavity 2 TM031. The usable range for the TE mode is higher than the respective for the TM mode.



Notice in general how the dielectric range increases for higher resonant modes, however compromising the measurement of the tangent loss due to lower quality factors because cavity losses.
For instance, observe that it is not possible to use the TE011 mode in the cavity 1 to characterize materials with permittivity values higher than 1.6 using a dielectric rod of 3 cm. However this situation can be solved if the dielectric rod diameter is reduced and, as consequence, the permittivity constant range increases. Figure 3 shows the new usable range using a dielectric rod of radius 2 cm for both Cavity 1 and Cavity 2.
This method is valid for each configuration cavity-resonant mode-dielectric rod, however due to the non- linearity of Equations (21) and (23), or equivalently (24) and (25) for TM modes, it results difficult to predict the percentage of increment in the valid usable range for dielectric measurements due to a reductions in the dielectric rod’s diameter.
Here it is easily observable how the usable range is increased, allowing to carry out measurements of higher permittivity values. This method is in general valid for any mode and resonant frequency.
Some authors do not use TM modes because any air gap between the top surface of the central cylindrical sample and the top surface of the external cavity can distort deeply the resonant frequency [15] .
One important aspect worth mentioning is that there are some flattened sections, portion with horizontal trends, of the curves shown in the Figures 2-4. Those portions represent regions of less sensitivity of the permittivity regarding the frequency measurement. This region is not a recommendable region to measure properties due to higher expected uncertainty associated to the measurement according results given in [19] and [20] . However the method shown in this article to determine the usable range of a given cavity can be used to avoid those regions of higher associated uncertainty, simply changing the diameter of the dielectric rod and hence the position in the curve of the expected permittivity under measurement. This result may be of the interest for metrology in dielectric permittivity.
5. Experimental Realization
In this section we explored the previous results by using a double-cylindrical dielectric resonator, diameter is 


Based on references [23] -[25] we expected a value to be lower than 4. It can be noticed in the Figure 5 that an adequate radius for this purpose is 3 cm. It is not recommended a large radius due to the simple fact that the
Figure 5. Usable range for dielectric measurement for a resonant cavity at 5 GHz in the mode TE011 for two radius: (a) 1 cm; (b) 3 cm. It is obvious that the recommended one is 3 cm which provides enough range for the characterization. Both radius where selected in this analysis according material availability.
resonant frequency of the cavity is lowered implying an electromagnetic characterization at another frequency than the required.
The real effective dielectric determined using the method of the critical points is 2.688 and the corresponding for heavy oil is 2.356 in total agreement with the tend of the previous results known for lower frequencies.
6. Conclusion
In this paper we presented a general methodology which may be useful to determine the usable dielectric range for material characterization. Due to the presence of the central cylinder, a displacement of the resonant fre- quency occurs proportional to the permittivity constant of the material until the resonant pattern of the mode under study can no longer exist. It means that for a given cavity and fixed rod’s radius to be located at the center of the cavity there exists a maximum value of measurable permittivity constant. No resonant conditions can be satisfied for higher permittivity values. The best alternative in order to increase the range of permittivity constant that can be measured reducing the radius of the central dielectric rod or choosing a higher resonant mode with the disadvantage that cavity loses can affect the results by changing the resonant frequency and the quality factor. We have shown that the behavior of the resonant frequency versus the dielectric constant should be taken into account when selecting the best appropriate region with high sensitivity in order to ensure the repeatability of measurement and to reduce the uncertainty associated to the measurement. Finally we have shown with a simple example the electromagnetic characterization of heavy oil with 11 API selecting a proper radious for a petroleum holder made of quartz of purity 99%.
Acknowledgements
This work was supported by FONACIT under the project No. 2011001317. We wish to thank to Roque Rodríguez for his contribution in this work.
References
- Love, D.C. and Rothwell, E.J. (2006) A Mode-Matching Approach to Determine the Shielding Properties of a Doubly Periodic Array of Rectangular Apertures in a Thick Conducting Screen. IEEE Transactions on Electromagnetic Compatibility, 48, 121-133.
- Massaro, A., et al. (2009) Design and Modeling of GaAs/AlGaAs Nonlinear Waveguides by Hertzian Potential Formulation. European Microwave Conference, Rome, 29 September 2009-1 October 2009, 719-722.
- Yla-Oijala, P., Taskinen, M. and Sarvas, J. (2001) Multilayered Media Green’s Functions for Mpie with General Electric and Magnetic Sources by the Hertz Potential Approach. Progress in Electromagnetics Research, 33, 141-165. http://dx.doi.org/10.2528/PIER00120802
- Tartarini, D. and Massaro, A. (2011) GPU Approach for Hertzian Potential Formulation Tool Oriented For Electromagnetic Nanodevices. Progress in Electromagnetics Research M, 17, 135-150.
- Collin, R.E. (1960) Field Theory of Guided Waves. 2nd Edition, IEEE Antennas and Propagation Society, USA.
- Gershon, D., Calame, J.P., Carmel, Y. and Antonsen, T.M. (2000) Adjustable Resonant Cavity for Measuring the Complex Permittivity of Dielectric Materials. Review of Scientific Instruments, 71, 3207-3209. http://dx.doi.org/10.1063/1.1304865
- Chen, L.J. and Lue, J.T. (1998) The Transition from the d- to s-State Due to Thermal Fluctuation for High-Tc Superconductors as an Evidence from the Microwave Penetration-Depth Measurement. IEEE Transactions on Microwave Theory and Techniques, 46, 1251-1256.
- Pozar, D.M. (2005) Microwave Engineering. 3rd Edition, John Wiley & Sons, Inc., Hoboken.
- Kukharchik, P.D., Serdyuk, V.M. and Titovitsky, J.A. (2008) Diffraction of Hybrid Modes in a Cylindrical Cavity Resonator by a Transverse Circular Slot with a Plane Anisotropic Dielectric Layer. Progress in Electromagnetics Research, 3, 73-94. http://dx.doi.org/10.2528/PIERB07112502
- Shen, Z.Y., et al. (1992) High-Tc-Superconductor-Sapphire Microwave Resonator with Extremely High Q-Values up to 90 K. IEEE Transactions on Microwave Theory and Techniques, 40, 2424-2431.
- Liu, J.H., Chen, C.L., Lue, H.T. and Lue, J.T. (2003) A New Method Developed in Measuring the Dielectric Constants of Metallic Nanoparticles by a Microwave Double-Cavity Dielectric Resonator. IEEE Microwave and Wireless Components Letters, 13, 181-183. http://dx.doi.org/10.1109/LMWC.2003.811668
- Yan-Shian, Y., Juh-Tzeng, L. and Zhi-Ren, Z. (2005) Measurement of the Dielectric Constants of Metallic Nanoparti- cles Embedded in a Paraffin Rod at Microwave Frequencies. IEEE Transactions on Microwave Theory and Techniques, 53, 1756-1760.
- Stratton, J.A. (1941) Electromagnetic Theory. McGraw-Hill Boook Company, USA.
- Geyi, W. (2008) Time-Domain Theory of Metal Cavity Resonator. Progress in Electromagnetics Research, 78, 219- 253. http://dx.doi.org/10.2528/PIER07090605
- Ong, C.K., Varadan, V.V. and Varadan, V.K. (2004) Microwave Electronics Measurement and Materials Characterization. John Wiley & Sons Ltd., Chichester.
- Dester, G.D., Rothwell, E.J., Havrilla, M.J. and Hyde, M.W. (2010) Error Analysis of a Two-Layer Method for the Electromagnetic Characterization of Conductor-Backed Absorbing Material Using an Open-Ended Waveguide Probe. Progress in Electromagnetics Research B, 26, 1-21. http://dx.doi.org/10.2528/PIERB10080506
- Krupka, J., Gregory, A.P., Rochard, O.C., Clarke, R.N., Riddle, B., et al. (2001) Uncertainty of Complex Permittivity Measurements by Split-Post Dielectric Resonator Technique. Journal of the European Ceramic Society, 21, 2373-2676. http://dx.doi.org/10.1016/S0955-2219(01)00343-0
- Riddle, B., Baker-Jarvis, J. and Krupka, J. (2003) Complex Permittivity Measurements of Common Plastics over Variable Temperatures. IEEE Transactions on Microwave Theory and Techniques, 51, 727-733.
- Paez, E., Azpurua, M.A., Tremola, C. and Callarotti, R.C. (2012) Uncertainty Estimation in Complex Permittivity Measurements by Shielded Dielectric Resonator Technique Using the Monte Carlo Method. Progress in Electromagnetics Research B, 41, 101-119. http://dx.doi.org/10.2528/PIERB12041306
- Paez, E., Azpurua, M.A., Tremola, C. and Callarotti, R.C. (2012) Uncertainty Minimization in Permittivity Measurements in Shielded Dielectric Resonators. Progress in Electromagnetics Research M, 26, 127-141. http://dx.doi.org/10.2528/PIERM12082811
- Harrington, R.F. (1961) Time-Harmonic Electromagnetic Fields. John Wiley and Sons, Hoboken, 220.
- Sun, E.Y. and Chao, S.H. (1995) Unloaded Q Measurement―The Critical-Points Method. IEEE Transactions on Microwave Theory and Techniques, 43, 1983-1986. http://dx.doi.org/10.1109/22.402290
- Callarotti, R.C. and Paez, E.J. (2014) Microwave Dielectric Properties of Heavy Oil and Heating of Reservoirs. SPE Energy Resources Conference, Port of Spain, 9-11 June 2014, 127-141. http://dx.doi.org/10.2118/169937-MS
- Callarotti, R.C. and Paez, E.J. (2013) Efficient Eigenvalue Numerical Solutions for Time Dependent Linear Systems. Computational Methods and Experimental Measurements, 16, 43-54.
- Paez, E.J., Callarotti, R.C., Azprua, B.M. and Rodrguez, R.J. (2013) Medida de la permitividad de lquidos de bajas prdidas en un resonador dielctrico blindado en alta frecuencia (4881 GHz). In 10 Congreso internacional de metrologa elctrica, Buenos Aires, September 2013, Vol. 10.







