Received 31 January 2015; accepted 5 May 2015; published 6 May 2015

ABSTRACT

Solid-core silica photonic crystal fiber is proposed borrowing the concept of golden ratio (1.618) and keeping it between pitch and air hole diameter 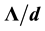in a subset of six rings of air-holes with hexagonal arrangement. In the case when we have a pitch equal to one micron (Λ = 1 μm), we need air-holes diameters d = 0.618 μm in order to achieve two zero dispersion wavelength (ZDW) points at 725 nm and 1055 nm; this gives us the possibility to use the fiber for supercontinuum generation, by pumping close to that points, pulse compression or reshaping. We analyzed a series of fibers using this relation and showed the possibilities of tunable ZDW in a wide range of wavelengths from 725 nm to 2000 nm, with low losses and small effective area. In agreement with the ZDW point needed, the geometry of the structure can be modified to the point of having only three rings of air holes that surround the solid core with low losses and good confinement mode. The design proposed here is analyzed using the finite element method with perfectly matched layers, including the material dispersion directly into the model applying the Sellmeier’s equation.

Keywords:

Photonic Crystal Fibers, Supercontinuum Generation, Zero Dispersion Wavelength

1. Introduction

Today the necessities for different applications in science and engineering of photonic crystal fibers (PCF) have boosted proposals on novel designs that satisfy specific conditions of linear and non-linear properties. Because of this, the control of dispersion, losses, mode confinement and conditions for generation of supercontinuum or pulse reshaping is a wide field of research. A series of techniques implying modification of some parameters of the fiber for various applications have been published. Since the invention of PCFs [1] [2] , their designs and applications have been increased. However, some structures suffer from complex geometry. Traditionally optical fibers are used in various applications, for instance, to transport laser energy for material machining, as a gain medium in fiber lasers or optical telecommunication [3] . However, new possibilities of applications arise when nonlinear properties of PCFs are manifested. Specifically, nonlinearities in PCFs allow new light sources with very broad spectra, i.e., supercontinuum generation (SCG) [4] [5] . The possibility to control group velocity dispersion (GVD) in PCFs, their small effective area and elevated nonlinearity [6] has allowed the observation of SCG in a much wider range of source parameters than has been possible with bulk media or conventional fibers [7] . It is known that in the case of normal GVD is present in the PCFs, the Raman scattering effect and self-phase modulation (SPM) dominate the spectrum broadening [8] , and soliton dynamics govern spectral broadening when central wavelength of the propagating pulse is in anomalous GVD. Finite element and finite-difference methods as well as the multipole method and the plane wave expansion method [9] [10] were used to characterize the electromagnetic field distribution in PCFs. The accurate control of the dispersion characteristics is obligatory in variety of applications, such as pulse recompression [11] mode locked fiber lasers [12] , nonlinear effects, including Raman scattering, four-wave mixing, SPM or soliton generation [13] , and SCG [5] [7] . The flexible geometry of PCFs offers many unique and novel dispersion properties in comparison to conventional single mode fibers such as nearly zero ultraflattened dispersion [14] -[16] , high negative chromatic dispersion [17] , and anomalous dispersion in short-wavelength regime [18] . As is known, the chromatic dispersion coefficient of an optical fiber is a key quantity in various analysis and design issues in fiber transmission systems [19] [20] .

According to the guidance mechanism, PCFs can be divided into two categories: first, total internal reflection (TIR), where air holes surround a high index solid core, and second, photonic band gap (PBG), where the light is confined to a central air hole [21] . In PCFs, the cladding region is usually formed by array of air holes in a regular triangular lattice with separation Λ [22] . Although there is a rich nomenclature of PCFs at this moment, we will restrict ourselves to index-guiding PCFs. In this kind of fibers, the core index is greater than the average index of the cladding because of the presence of air holes, and the fiber can guide the light by total internal reflection as a standard fiber does. That is, the guided mode has effective index 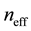that satisfies the condition

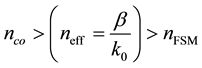(1)

where 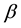is the mode propagation constant, 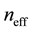is the core index, and 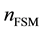is the cladding effective index, which is termed also the effective index of the fundamental space-filling mode (FSM). In case of a PCF made of pure silica, 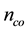is the refractive index of silica. The losses in PCFs occur due to intrinsic material absorption, structural imperfection, Rayleigh scattering, and imperfect confinement. Fabrication-related losses can be reduced by carefully optimizing the fabrication process [23] . Confinement losses are an additional form of energy leakage that occurs in single-material fibers because of inherently leaky nature of the guided modes in these fibers [24] . This is because the core index is the same as the index of the outer cladding without air holes. Confinement losses can be reduced by increasing the number of rings of air holes which surround the solid core, and thus are determined by the geometry of the structure. It is important to know how many rings of air holes are required to reduce the confinement loss under the Rayleigh scattering limit. At the same time, geometry of the structure allows the chromatic dispersion to be easily controlled by varying the air hole diameter and the pitch of PCF. Here we show that some properties such as losses, ZDW and intermodal dispersion can be controlled keeping the ratio between fiber pitch and hole diameter of the microstructured cladding equal to the called number golden ratio, i.e., 1.618.

Controllability of chromatic dispersion in PCFs is a very important problem for practical applications in optical communication systems, and nonlinear optics. The chromatic dispersion profile can be easily controlled by varying the values of any or all of the following parameters: air hole diameter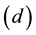, pitch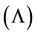, number of rings (Nr) and the number of missing holes (MNr). The aim of this work is to demonstrate how the dispersion profile may be modified by variation of the pitch and the hole diameter, keeping the golden ratio between them, i.e., keeping a ratio between them equal to 1.618, providing a tunable ZWD in the range of 725 nm to 2000 nm.

2. Characteristics of the Fiber

Figure 1 shows the geometry of the solid core PCF proposed for SCG. The PCF consists of an arrangement of six rings with hexagonal structure and pitch size from 1 to 2 μm (Λ) and air hole diameter from 0.618 to 1.236 μm. This PCF has small effective area and tunable zero wavelength dispersion points in the range from 725 to 2000 nm. Although PCFs can be characterized by variety of methods including finite-difference time-domain method [25] we have used finite-element (FEM) approximation of the Helmholtz equation applying Sellmeier’s equation to take the material dispersion into account when calculating effective mode index. The curve of total chromatic dispersion of the PCFs is obtained using following expression

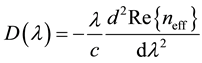(2)

where 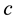is the speed of light in vacuum, 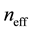is the effective mode index, and 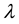is the radiation wave- length.

This structure, proposed to tune the ZDW coinciding with the pump laser wavelengths to facilitate SCG or pulse reshaping applications, is inspired by the nature where the golden ratio can be found in perfect structures of the leaves, animals or the human body. Thus, we propose to use such a golden ratio in the design of a PCF and evaluate its impact on the optical properties. When this proportion is satisfied in the nature, the efficiency of the structures in macro- and micro-world is increased a lot, independently of the eye appeal. Talking about micro-world, we can found the golden ratio in the structure of some viruses, living cells, deoxyribonucleic acid, and bodies of honey bee, leaves or animals. In the macro-world, golden ratio can be found in the structure of galaxies. Due to this we probed to use the golden ratio for synthesis of photonic microstructures just like it happened in architecture to create some design of buildings, for example, keeping this relation. We found that this relation can improve the properties of the PCF; when we keep pitch-to-hole-diameter ratio equal to the golden ratio, it helps us to obtain simpler structures with better characteristics corresponding to the application of need.

In Figure 2 and Figure 3 we show the effective area and nonlinear coefficient of the designed PCF with the pitch Λ = 1, 1.5, 2 μm and air-holes diameter d = 0.618, 0.927, 1.236 μm. Using only six rings of air holes surrounding the solid core we have good confinement of the fundamental mode, small effective area, and high nonlinear coefficient. The structure keeps the golden ratio between pitch and diameter, and with this, we achieve

an improvement of the characteristics of PCF correspondingly to an application needed. The effective area and the nonlinear coefficient have been calculated applying the concepts of conventional fiber theory [26] with modifications necessary to include photonic-crystal cladding into account [26] -[28] .

(3)

(4)

(5)

(6)

where is the effective core radius, is the operating wavelength, is the core index, is the effective index of the fundamental space-filling mode, is the half of mode field diameter (MFD) called also the effective modal spot size, is the effective mode area, is the correction factor [29] , is the nonlinear coefficient [30] and is the nonlinear index of silica. In Section 4 we show an application of the supercontinuum generation using this specific value of nonlinear coefficient shown in Figure 3.

3. Tunable Zero Dispersion Wavelength

In Figure 4 we show the calculated total chromatic dispersion obtained using submicron air hole diameters in order to keep the golden ratio parameter. We can see that varying the pitch from 1 to 1.5 μm two different ZDW points are obtained which are tunable depending on the value of the pitch. Moreover, the curve becomes more gently sloped with increasing the value of pitch, giving the possibility to use this kind of fiber in different applications. In Section 4 we use this design in simulation of super continuum generation. The curves show a maximal chromatic dispersion from 38 to 80 ps/(nm*km) and always we obtain two ZWD points which can be used for pumping by two different lasers to generate a more wide and flattened SC spectrum [31] -[33] .

In Figure 5 we show chromatic dispersion curves obtained when air hole diameters exceed 1 μm. Therefore, the pitch shall be from 1.618 to 2 μm in order to maintain the golden ratio proportion. The curves shows a maximal chromatic dispersion from 85 to 90 ps/(nm*km), and, as in the previous case, we always have two ZWD points in the range of 725 - 2000 nm. We believe that fabrication of this kind of fiber is simple due to micrometric scale of the constituents.

4. Simulation of Super Continuum Generation, Pulse Reshaping and Compression

The PCFs proposed here were analyzed using commercial software COMSOL Multiphysics which uses the proven finite element method (FEM). This software runs the finite element analysis together with adaptive meshing and error control using a variety of numerical solvers. The RF Module of COMSOL provides the capabilities to design and is used to simulate electromagnetic wave propagation in PCFs. The mode analysis is made on a cross-section in the xy-plane of the fiber, by expressing the propagating wave in z direction in the following form

(7)

and, thereupon, solving the homogeneous Helmholtz equation

(8)

for the eigenvalue applying circular perfectly matched layer, with being the propagation constant.

The pulse propagation in the PCFs is numerically investigated within the Generalized Nonlinear Schrödinger Equation (GNLSE) [34] [35]

(9)

where is the attenuation constant, is the complex field envelope, is the distance, is the retarded time traveling at the envelope group velocity, is the nonlinear coefficient and are the dispersion coefficients obtained by a Taylor series expansion of the propagation constant around the center frequency. The GNLSE is solved by Fourth-Order Runge-Kutta in the Interaction Picture Method (RK4IP) [36] [37] .

The Raman response function for silica fibers is described by [38]

(10)

To simulate the super continuum generation we consider the waveform with the full width at half maximum (FWHM), T_FWHM = 50 fs, and 10 kW of peak power and 873 nm, propagating into a 5-mm length of a PCF with maximal chromatic dispersion at 873 nm of 39.78 ps/(nm*km). The PCF designed has low losses, small effective area (A_eff = 1.76 μm² at 873 nm), and large nonlinear coefficient in the range of 800 to 1600 nm. Pulse evolution has been simulated using RK4IP method for solution of the generalized nonlinear Schrödinger equation The fiber parameters used in the calculation are given as, , , , , in which we achieve a more wide spectrum that reported using similar parameters.

Figure 6 shows the super continuum spectrum obtained by simulation of ultra short pulse propagation in the designed PCF, where we use the property of anomalous dispersion with high nonlinear coefficient of the PCF proposed, for creation a wide spectrum using femtosecond pump laser and shorter length of PCF. We can see a relatively smooth spectrum and wide SC spectrum of 2100 nm bandwidth at the level of −40-dB. In Figure 7 we show temporal evolution of the pump pulse. We observe that soliton-like pump pulse has broken onto seven waveforms which can be interpreted as pulses; it gives the output pulse a form of the train of very short pulses. Taken this observation into account together with the fact that wavelength of the pump pulse is in anomalous dispersion region of the PCF designed, we conclude that Figure 7 show us manifestation of the soliton fission, which is known as a primary nonlinear effect under these propagation conditions [7] . In the spectral domain the

soliton fission manifests itself as an extreme broadening of the spectrum of incident pulse. It is exactly what we observe in Figure 6. Thus, the main effect of spectral broadening in our case is the soliton fission.

The structure of the PCF designed has also been used for investigation of a possibility of pulse compression and transformation of the pulse shape supposing a sech² initial pulse envelope (IPE) waveform. Each of these applications requires a particular combination of dispersion and nonlinearity. Transformation of pulse to another high-quality waveform in a fiber requires usually a normal dispersion at the central wavelength of the incident pulse [8] [39] , as the primary phenomenon in this case is an interplay between the self-phase modulation and normal dispersion [8] [40] -[42] . Therefore, for simulation of pulse shape transformation we use following parameters and central wavelength of the pulse to be 600 nm: T_FWHM = 140 fs, peak power P = 8 kW, fiber length 13.5 mm, , , , , . The wavelength of 600 nm has been chosen because of all dispersion curves we obtained using golden ratio, demonstrate normal dispersion at this wavelength; and this is exactly what we need to achieve pulse transformation with sufficiently high quality of the output pulse.

All of golden-ratio combinations of pitch and hole diameter demonstrate highly nonlinear dispersion profile; therefore, those fibers cannot be applied directly to pulse compression like it made in case of chirped mirrors, for example [43] [44] . However, these combinations provide wavelength ranges with anomalous group velocity dispersion where formation of higher-order solitons is possible. Thus, within these ranges one can compress the pulse using soliton-effect compression [45] . This has been implemented for the case of Λ = 1.618 μm and air-holes diameter with five rings of holes in the cladding. In this case, zero dispersion wavelengths are 800 nm and 1956 nm, and maximum of the chromatic dispersion equals to 99.27 ps/(nm*km) @1303 nm, as shown in Figure 4. Other parameters are following: TFWHM = 250 fs @1303 nm, peak power P = 10 kW, , , , ,. The optimal length of the fiber when maximum compression is achieved, equals to 15 mm. The compression factor in this case equals to 100. Figure 8 shows the incident pulses for cases of shape transformation and compression, compressed pulse, and reshaped pulse with a flat-top waveform. The shape of the compressed pulse demonstrates a pedestal, which is typical for pulses obtained via soliton-effect compression. Spectra of corresponding output pulses are shown in Figure 9. Spectrum of the flat-top pulse demonstrates signatures of the self-phase modulation. This nonlinear effect together with normal group velocity dispersion at 600 nm produces flat top pulses. A closer look to the reshaped pulse in Figure 8 allows noting oscillations at the trailing edge of the pulse, which is manifestation of the optical wave breaking [46] . These results indicate a possibility to use the PCF proposed in variety of engineering problems of nonlinear optics.

5. Conclusion

In this work, we proposed to evaluate how the optical properties of a PCF were influenced when the proportion between pitch and diameter of holes was equal to the golden ratio. In particular, when this ratio is maintained and the pitch and diameter holes are varied, the ZDW could be tunable between the range of 725 nm to 2000 nm. Additionally, with a low number of rings, we obtain a small loss confinement with small effective area and high nonlinear coefficient. Finally, we obtain a flattened chromatic dispersion curve between of two ZDW points. We present an example of applications of this kind of designs for supercontinuum generation, pulse recompression and pulse reshaping. A good quality of flattened and wide spectrum is achieved. The spectrum possesses 2100 nm bandwidth at 40 dB level. The compression factor achieved is 100 producing a compressed pulse of 2.5 fs from an initial pulse of 250 fs. It is believed that the design proposed could be fabricated easily with techniques available nowadays.

Acknowledgements

This work was supported in part by the National Council for the Science and technology (CONACYT) of Mexico, and by Universidad de Guanajuato (project DAIP-192/13 and DAIP-430/2014), FOMIX (CONACyT & CONCyTEG) under grant GTO-2012-C04-195229 and DAIP 458/2014. A. Barrientos-García and J. Carlos Hernandez-Garcia are grateful to CONACYT for a student research grant No. 329409/336847 and CONACYT project no. 3155.

References

NOTES

^*Corresponding author.